Распознавание гомотопического типа объекта с помощью дифференциально-топологических инвариантов аппроксимирующего отображения
Автор: Курочкин Сергей Владимирович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Обработка изображений, распознавание образов
Статья в выпуске: 4 т.43, 2019 года.
Бесплатный доступ
Предложен новый метод топологического анализа данных, позволяющий получить информацию о гомотопическом типе анализируемого объекта. В отличие от наиболее хорошо разработанных и широко применяемых методов, использующих понятие персистентных гомологий, данный метод основан на анализе дифференциальных инвариантов аппроксимирующего отображения. Таким образом, в противоположность комбинаторно-топологическому подходу, используются методы дифференциальной топологии и прямая аналогия с основным результатом теории Морса. При этом аппроксимирующее графический объект гладкое отображение может быть построено с использованием общедоступного инструментария, например, нейронной сети. Доказано, в частности, что метод позволяет полностью распознать гомотопический тип объекта на плоскости: топологическая степень некоторого вспомогательного отображения и количество окружностей в гомотопически эквивалентном представлении объекта в виде букета связаны соотношением. Работа алгоритма продемонстрирована на примере символов из базы данных MNIST и их трансформаций. Рассмотрены обобщения и открытые вопросы, возникающие в случае более высоких размерностей.
Машинное обучение, топологические инварианты, степень отображения, обработка изображений
Короткий адрес: https://sciup.org/140246493
IDR: 140246493 | DOI: 10.18287/2412-6179-2019-43-4-611-617
Текст научной статьи Распознавание гомотопического типа объекта с помощью дифференциально-топологических инвариантов аппроксимирующего отображения
Топологический анализ данных (TDA) [1, 2] имеет целью выявление и изучение наиболее «грубых» («существенных», «устойчивых», «инвариантных» и т.д.) свойств точечных множеств в многомерных пространствах – именно таких, которые не зависят от выбора системы координат и инвариантны относительно непрерывных деформаций объекта и/или пространства признаков. В последние годы в связи постановкой всё более сложных задач анализа многомерных, зашумлённых и плохо структурированных данных направление привлекает большое внимание исследователей и практиков, о чём свидетельствует интенсивный поток публикаций. В частности, TDA стал важной составляющей проекта DARPA [3–5].
В настоящее время основным рабочим инструментом TDA является вычисление гомологий симплици-альных комплексов, связанных с исследуемым объектом. Кратко суть метода состоит в следующем. Для некоторого параметра ε>0 берётся покрытие множества ε-шарами и строится его комплекс Чеха (как нерв покрытия) или же (несколько иным и вычислительно более выгодным способом) комплекс Вието-риса–Рипса. Затем вычисляются гомологии комплекса. Процедура эффективно реализуется численно, однако содержит произвол в выборе параметра. Здесь работает идея persistence [6] (русский термин не сложился, по смыслу – устойчивость, неизменность). Нужно рассмотреть гомологии для различных ε (теоретически – для всевозможных) и естественные отоб- ражения этих групп для ε1 <ε2 (вся конструкция вместе образует т.н. фильтацию). Persistent-существенными являются те элементы групп гомологий, которые сохраняются (т.е. изоморфно отображаются из прообраза в образ, а не обнуляются и не возникают)
на достаточно длинных промежутках изменения параметра. Идея persistence перекликается с похожим приёмом в методе кластерного анализа: «истинными» кластерами объявляются те, конфигурация которых соответствует длинным горизонтальным (без слияний) участкам диаграммы кластеров. Следующие рисунки (источник [1]) иллюстрируют метод.
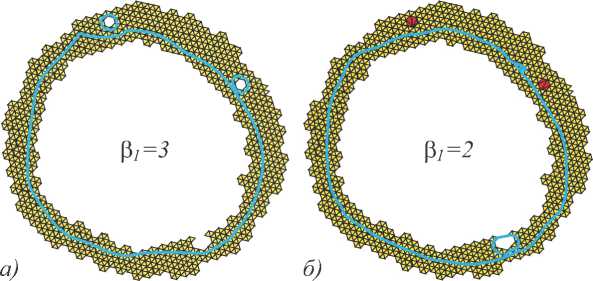
Рис. 1. Персистентные гомологии
Представлено одно и то же точечное множество на плоскости и его комплексы Чеха для двух различных значений параметра (на рис. 1а меньше, чем на рис. 1б). Визуально ясно, что объект, выборку из которого представляет множество, гомеоморфен окружности. Однако при анализе его дискретного представления возникают хорошо видимые «паразитные» циклы – два на первом рисунке и один на вто- ром. Формально вычисленные числа Бетти (соответственно 3 и 2) для исходного объекта неверны. Правильное значение можно узнать, рассмотрев естественное отображение группы гомологий левого комплекса в группу правого: два маленьких цикла на левом рисунке перейдут в ноль («заклеиваются»), маленький цикл на правом рисунке не будет иметь прообраза («возникает»), и только истинный цикл отобразится изоморфно.
Разработка и практическая реализация методов описанного класса включает в том числе преодоление различных технических трудностей и неестественных эффектов. Например, на плоскости можно построить точечное множество, чей комплекс Виеториса–Рипса будет гомеоморфен сфере S n любой наперёд заданной размерности n , см. [7].
В данной работе предложен подход к задаче топологического анализа данных, основанный на другой математической идее и конструкции: свойства объекта можно узнать, изучая функции, заданные на нём. Эта идея плодотворно работает в различных разделах математики. Возможно, самым ярким примером её применения (и близким к теме данной работы) является основной результат теории Морса [8, 9]: гомотопический тип компактного связного многообразия можно узнать, имея информацию о критических точках (их количестве и индексах) всего одной произвольно взятой («общего положения») гладкой функции на этом многообразии.
Привлекательность предлагаемого подхода связана с тем, что к настоящему времени хорошо разработаны и реализованы в виде, доступном даже для неквалифицированного пользователя, различные методы построения аппроксимирующих/сглаживающих отображений. Обычно при этом используются нейронные сети или методы типа local fit. Таким образом, почти вся техническая составляющая метода уже оказывается в распоряжении исследователя, и необходимо лишь – как в теории Морса – найти конечное множество точек, по которым можно вычислить степень отображения и посчитать их индексы.
Целью и результатом предлагаемого метода анализа является определение гомотопических свойств анализируемого объекта, в наилучшем случае (для случая плоскости, см. далее) – его гомотопического типа. Эта классификация более грубая, чем с точностью до гомеоморфизма. Однако в этом отношении методы, основанные на вычислении гомологий аппроксимирующих комплексов, дают не больше информации об объекте, поскольку (см., например, [9]) у гомотопически эквивалентных пространств гомологии одинаковы.
Инструментом анализа выступают некоторые дифференциально-топологические инварианты, связанные с аппроксимирующим отображением.
Структура работы следующая. В параграфе 1 изложена математическая конструкция. Сформулирован и доказан основной результат. В параграфе 2 метод применён к задаче анализа изображений из известной те- стовой базы данных. Сделано это с целью продемонстрировать принципиальную работоспособность метода в хорошо известной специалистам и полностью реплицирумой ситуации. В заключение представлены некоторые выводы и открытые вопросы.
-
1. Связь дифференциальных свойств аппроксимирующего отображения с гомотопическим типом объекта
В качестве предмета классификации могут выступать объекты с формально различным математическим описанием, в том числе (список неполон):
-
1) «достаточно хорошие», например, клеточные, подпространства евклидовых пространств; пример – плоский граф;
-
2) чёрно-белые растровые изображения;
-
3) растровые изображения с оттенками серого, изначально представляющие чёрно-белый (графический) образ; последнее требование означает отсутствие больших областей серого цвета и сёдел (см. ниже замечание к п. 4 схемы метода и параграф 2);
-
4) точечные подмножества евклидовых пространств, имеющие метрическую размерность меньше, чем у объемлющего пространства [10].
Далее потребуются некоторые топологические понятия, изложение которых можно найти в учебниках, см., например, [9]. В этом абзаце дана краткая справка. Два непрерывных отображения f 0 , f 1 из X в Y , где X , Y – топологические пространства, называются гомотопными (принадлежат одному гомотопическому классу), если существует непрерывное отображение F : [0, 1] × X → Y такое, что F [0, . ] ≡ f 0 , F [1, . ] ≡ f 1 . Пространства X , Y гомотопически эквивалентны (имеют один гомотопический тип), если существуют непрерывные отображения f : X → Y и g : Y → X такие, что f ◦ g и g ◦ f гомотопны тождественным отображениям соответственно в X и Y . Ретракция – непрерывное отображение топологического пространства X на его подмножество M , тождественное на M . Деформационная ретракция – ретракция, гомотопная тождественному отображению X . Используются также некоторые известные топологические факты, они приводятся далее в контексте.
Опишем схему метода для двумерного случая (про общий случай будет сказано далее).
-
1. Пусть дано связное компактное подмножество A евклидовой плоскости ( x , y ).
-
2. Пусть функция h (.) – индикатор множества A : h ( x , y )= 1, если точка ( x , y) принадлежит A , 0 – не принадлежит.
-
3. Аппроксимируем h гладкой функцией f . Поскольку A ограничено, можно добиться, чтобы f была тождественно нулём вне некоторого круга. Тем самым можно считать, что f определена на сфере, которая получается добавлением к плоскости бесконечно удалённой точки.
-
4. По функции f строим отображение φ двумерной сферы в себя следующим образом: φ ( x , y ) есть точка, в которой луч с направляющим вектором
-
5. Гомотопический тип «достаточно хорошего» (например, клеточного) связного компактного множества на плоскости есть букет окружностей (несколько окружностей, склеенных по точке).
-
6. Гомотопический класс отображения сферы в сферу той же размерности (речь идёт об отображении φ) полностью определяется одним целочисленным инвариантом – степенью отображения. Степень отображения (допуская некоторую вольность речи) может быть определена как количество (со знаками) прообразов произвольно взятой («общего положения») точки из образа, причём каждый прообраз учитывается со знаком «+», если отображение в этой точке сохраняет ориентацию, и «-», если обращает. Точные формулировки см., например, в [9], Глава 1, § 10, п. 3.
-
7. В реальных задачах степень φ может быть вычислена конструктивно. Например, у точки (1,0,0) в общем случае будет конечное число прообразов относительно φ. В терминах отображения f это такие точки ( x , y ), что: f ( x , y )= 1/2, т.е. серый цвет; f ' x ( x , y )>0; f ' y ( x , y )= 0, т.е. переход от белого к чёрному слева направо. Расположение таких прообразов может быть найдено известными методами поиска решения для нелинейных уравнений. В случае (как далее в примере в параграфе 2), когда для f используется её дискретная аппроксимация, следует искать точки сетки, где выполняются приближённые соотношения f ( x , y )≈ 1/2, f ' x ( x , y )>0, f ' y ( x , y )≈0 . При удовлетворительном качестве аппроксимации такие точки будут образовывать кластеры, причем каждый кластер будет соответствовать одному истинному прообразу. Эти кластеры могут быть найдены обычными методами кластерного анализа. После нахождения прообразов следует определить в них знаки гессиана функции f и просуммировать (см. п. 6).
-
8. Гомотопический тип исходного объекта (п. 5) однозначно восстанавливается по информации п. 6, см. теорему далее.
( f ' x ( x , y ), f ' y ( x , y ), f ( x , y )- 1/2) пересекает единичную сферу; φ(∞)= южному полюсу.
Замечания.
К п. 1. Разделение компонент несвязного множества удовлетворительно делается методами кластерного анализа.
К п. 2. Вариант: дано не само множество, а гладкая функция f , выражающая какую-то «меру» или «вероятность» для точки ( x , y ) принадлежать ему. Тогда переходим к пункту 3. Другой вариант: дано не A, а функция ħ , заданная на выборке точек плоскости и принимающая значения в промежутке [0,1]. Тогда в п. 3 аппроксимируем ħ , а не h .
К пп. 3 –4. Здесь проясняется, какие требования нужно предъявить к исходному множеству и/или способу аппроксимации его индикатора. Множество должно быть в достаточной степени «контрастным» – так, чтобы его функция плотности не имела больших полутоновых областей и сёдел. Аппроксимирующая функция f может быть получена конструктивно (см. Введение). Далее, три координаты вектора в определении φ не должны обращаться в ноль одновременно. По существу это вытекает из требований к множеству, а формально является свойством общего положения и будет удовлетворяться в реальных ситуациях. Однако для строго обоснования последующих действий и инвариантности результата относительно способа аппроксимации необходимо уточнить требования к последнему. Например, достаточно предположить следующее: для некоторого δ, 0<δ< 1/2 , множество A есть деформационный ретракт множества f -1{[1/2 + δ, 1]} и отрезок [1/2 - δ, 1/2 +δ] не содержит критических значений f, см. [11, Теорема 2.2] и [12, Лемма 25.1.1]. Что касается вычисления частных производных, то формально информация о них содержится в параметрах функции f. По существу же, для сложно устроенных отображений, например, нейронных сетей, такое вычисление – в соответствующей литературе фигурирует как «оценка чувствительности к признакам» – является отдельной, не всегда тривиальной и хорошо осознанной задачей. Одним из известных подходов является генерирование дополнительной подвыборки в окрестности интересующей точки и прогон на ней обученной сети [13]. Здесь, в зависимости от специфики задачи, возможны различные решения и дополнительные исследования. Далее в изложенном в параграфе 2 примере используется численное дифференцирование сеточной функции.
К п. 5. Гомотопический тип связного плоского графа есть букет 1 -χ окружностей, где χ – его эйлерова характеристика, χ= V - E , V – количество вершин, E – количество рёбер [14, Теорема 2.3.13]. Или, как следствие общего факта, [9, Глава 1, § 5]. Произвольный многоугольник на плоскости деформационно ретра-гируется на некоторый граф [15, Лемма 3.12] и, следовательно, имеет тот же гомотопический тип. Для реальных объектов утверждение интуитивно очевидно и практически выполняется. Так, в шрифте, которым набран этот текст, цифры 1, 2, 3, 5, 7 имеют гомотопический тип «точка» (букет нулевого количества окружностей), 0, 4, 6, 9 – одна окружность, 8 – букет двух окружностей. Результат верен независимо от того, рассматриваются ли символы как топологические графы, или как имеющие толщину линий, или как растровые изображения.
Основной результат.
Теорема. В сделанных предположениях относительно A и f количество s окружностей в букете, описывающем гомотопический тип A , и степень deg (φ) отображения φ связаны соотношением: s = 1 - deg (φ) .
Доказательство. Дополнение к A состоит (см. [14, Глава 2, Теоремы 2.3.12, 2.3.13]) из s + 1 связных компонент, из которых одна – U∞ – является окрестностью бесконечности, а остальные – U1, ..., Us – ограниченные области, гомеоморфные диску. Выберем в каждой из компонент Uk по одной точке zk и её круговую окрестность Vk, целиком лежащую в Uk; для k =∞ положим z∞=∞ и V∞= {(x, y): x²+ y²> m}, где m >>diam(A). Функцию f можно гладко деформировать в функцию f1, равную единице вне объединения Vk, ну- лю во всех zk, а внутри Vk гладко и монотонно зависящую от расстояния точки-аргумента до zk (для k =∞ – монотонно стремящуюся к нулю при x²+ y²→∞). При этом отображение φ гладко деформируется в соответствующее отображение φ1. Поскольку степень инвариантна относительно гомотопий, deg(φ) = deg(φ1) . Но степень φ1 легко посчитать непосредственно: например, у точки сферы (1,0,0) будет относительно φ1 ровно s + 1 прообразов, по одному в каждом Vk. При этом прообраз, расположенный в V∞, будет иметь положительный знак якобиана, а все остальные (если таковые имеются, т.е. при s >0) – отрицательный. Следовательно, степень φ равна 1 - s. □
В общем случае, т.е. когда A есть подмножество евклидова пространства произвольной размерности n , конструкция метода сохраняется: так же строится отображение φ: Sn → Sn и вычисляется его степень, которая по-прежнему полностью описывает гомотопический класс φ. Однако положение здесь существенно сложнее тем, что уже нет простой гомотопической классификации для произвольных A . Как букеты ( n - 1)-мерных сфер теперь представляются только ( n -2)-связные подмножества [9], Глава 1, § 5]. Например, для трёхмерного пространства это его односвязные подмножества, и двумерный тор в эту классификацию не входит. Таким образом, гомотопический класс φ уже не определяет полностью гомотопический тип A . Тем не менее, степень φ всё равно содержит информацию об A , важную и саму по себе, и полезную в сочетании с иной информацией. Например, если a priori известно, что A – поверхность (двумерное связное компактное многообразие) в R ³, то можно показать, что deg(φ) = 2(1 - g ) , где g – род поверхности (количество ручек в представлении как сферы с ручками), то есть гомотопический (а с учётом априорной информации – и топологический) тип A полностью восстанавливается.
2. Пример распознавания гомотопического типа графического изображения
Рассмотрим пример применения предлагаемого метода к конкретным объектам – символам из известной базы данных MNIST [16], которая широко используется для тестирования методов распознавания изображений. Первый объект (символ «9», номер 44 из обучающего множества) представлен на рис. 2. По типу формального описания объект относится к случаю 3 (см. начало параграфа 1) – растровое изображение с оттенками серого. Следует отметить, что из-за плохого по современным требованиям (можно сказать, умышленно плохого) качества изображения данный случай не удовлетворяет требованиям применимости предлагаемого метода (см. параграф 1, замечание к п. 4 описания метода). А именно, видны и обнаруживаются при расчётах трудно устранимые серые фрагменты, имеется седловая область (на рисунке отмечена стрелкой).
Тем не менее, анализ по описанной схеме с некоторыми дополнительными действиями даёт правильный результат. Прежде всего, потребовалось проде- лать сглаживание по 9 точкам с равными весами, результат представлен на рис. 3а. Далее применялся алгоритм, частные производные вычислялись через разностное приближение f 'x (x, y)=[ f (x +1, y)– f (x -1, y)]/2
и соответственно для f ' y . На рис. 3 б представлены кластеры точек, в которых f ' x >0, а величины f ' y ( x , y ) / f ' x ( x , y ), ( f ( x , y )- 1/2) / f ' x ( x , y ) по модулю меньше некоторого порога (полагался равным 0,5), и указаны знаки якобиана отображения φ на этих кластерах (вторые производные f вычислялись через симметричные вторые разности). Шкалы по осям позволяют визуально оценить расположение и состав кластеров. Расчёты показали, что кластерный анализ вполне удовлетворительно проводится соответствующими известными методами, например, методом k -средних с выбором числа кластеров k при помощи
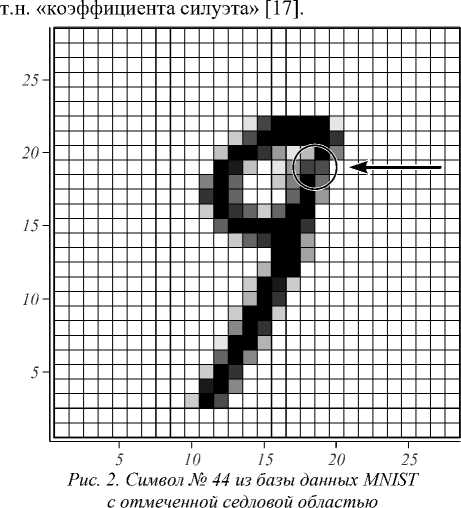
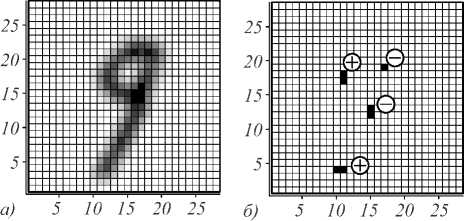
Рис. 3. Тот же символ, сглаженный по 9-точечной маске, и прообразы регулярного значения (1,0,0) относительно отображения φ с указанием знаков
Получаем, что deg(φ)=0 и, по Теореме, s = 1, что является верным ответом.
На рис. 4–6 представлены аналогичные результаты для различных трансформаций данного изображения, а на рис. 7–8 – для другого исходного объекта: MNIST, символ «8», номер 56 из обучающего множества, для которого s =2.
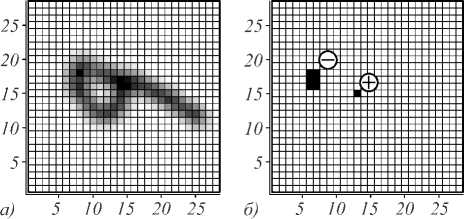
Рис. 4. То же, поворот на π/2
кластерная структура везде присутствует (что при столь плохом качестве материала заранее не очевидно), и во-вторых, везде получен верный результат.
Заключение
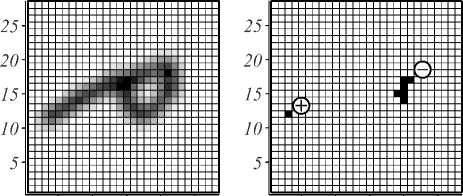
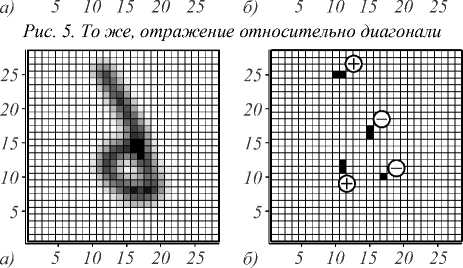
Рис. 6. То же, отражение относительно горизонтальной оси
Предложенный метод позволяет выявлять топологические свойства точечных множеств в евклидовом пространстве с помощью инструмента, легко доступного аналитику, а как правило – автоматически имеющемуся у него в распоряжении, – гладкой числовой функции, аппроксимирующей функцию-индикатор анализируемого множества. В некоторых случаях — произвольных множеств на плоскости, многообразий в пространстве – дифференциально-топологические свойства аппроксимирующей функции позволяют полностью восстановить гомотопический тип объекта. Предлагаемый способ для некоторых задач может оказаться вычислительно дешевле и проще в применении, чем мейнстрим-подход топологического анализа данных, основанный на вычислении устойчивых гомологий симплициальных комплексов Чеха или Виеториса–Рипса. В задачах же такого типа, как была рассмотрена в параграфе 2, то есть когда задано не точечное множество, а аппроксимирующая функция или её дискретизация, метод, как показано, может быть успешно применён, в то время как методы, предполагающие построение комплексов, не могут быть применены. В то же время, в сравнении с нейросетевыми методами распознавания и классификации, предложенный метод позволяет напрямую исследовать топологические характеристики объекта.
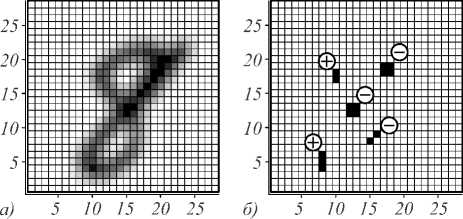
Рис. 7. Символ № 56 из базы данных MNIST (сглаженный) и кластеры прообразов регулярного значения
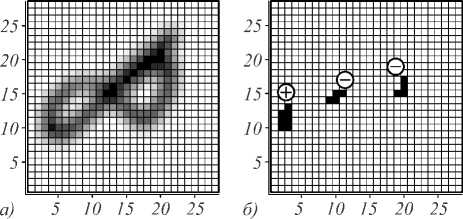
Рис. 8. То же, отражение относительно диагонали
Здесь уместно напомнить, что решается не задача распознавания образа, а задача распознавания его гомотопического типа. Как и следовало ожидать, в различных трансформациях объекта количество, расположение и знаки кластеров различаются, однако, во-первых,
По-видимому, дальнейшие усилия могут быть направлены на решение двух групп вопросов. Во-первых, в отличие от множеств на прямой и на плоскости, для множеств в многомерных пространствах отсутствует простая гомотопическая (тем более топологическая) классификация, что делает неопределённым формат требуемого ответа. Как и вообще в анализе данных, наибольшие трудности связаны с множествами, имеющими в разных своих участках разную размерность. Представляет интерес вопрос, в каких дополнительных предположениях или/и в сочетании с какой дополнительной информацией степень отображения φ позволяет определить топологические свойства объекта. Вторая группа вопросов проистекает из необходимости в данном методе знать первые частные производные аппроксимирующего отображения и даже некоторую информацию о вторых (нужен знак гессиана в конечном числе точек). При том, что способы сделать это будут неизбежно и существенно зависеть от метода аппроксимации, здесь – по аналогии с похожими ситуациями в других разделах вычислительной математики – могут быть найдены методы, позволяющие избежать собственно вычисления производных, а только диагностирующие их равенство/неравенство нулю и знак.
Работа выполнена в рамках реализации программы Центра хранения и анализа больших данных МГУ имени М.В. Ломоносова. Автор благодарен рецензенту первого варианта статьи за ценные замечания и рекомендации, позволившие улучшить текст.
Список литературы Распознавание гомотопического типа объекта с помощью дифференциально-топологических инвариантов аппроксимирующего отображения
- Carlsson, G. Topology and data / G. Carlsson // Bulletin of the American Mathematical Society. - 2009. - Vol. 46, Issue 2. - P. 255-308. - DOI: 10.1090/S0273-0979-09-01249-X
- Zomorodian, A. Topological data analysis / A. Zomorodian. - In Book: Advances in applied and computational topology / ed. by A. Zomorodian. - American Mathematical Society, 2012. - P. 1-40. - ISBN: 978-0-8218-5327-6
- Mervis, J. What makes DARPA tick? / J. Mervis // Science. - 2016. - Vol. 351, Issue 6273. - P. 549-553.
- DARPA - Frontiers of engineering [Electronical Resource]. - URL: https://www.naefrontiers.org/File.aspx?id=22017 (request date 30.10.2018).
- Рогозин, Д.О. Высокие технологии в США: Опыт министерства обороны и других ведомств. / Д.О. Рогозин, И.А. Шеремет, С.В. Гарбук, А.М. Губинский. - М.: МГУ, 2013. - 380 с.
- Edelsbrunner, H. Topological persistence and simplification / H. Edelsbrunner, D. Letscher, A. Zomorodian // Discrete and Computational Geometry. - 2002. - Vol. 28, Issue 4. - P. 511-533. -
- DOI: 10.1007/s00454-002-2885-2
- Adamaszek, M. On homotopy types of euclidean rips complexes [Electronical Resource] / M. Adamaszek, F. Frick, A. Vakili. - URL: https://arxiv.org/pdf/1602.04131.pdf (request date 30.10.2018).
- Постников, М.М. Введение в теорию Морса / М.М. Постников. - М.: Наука, 1971.
- Фоменко, А.Т. Курс гомотопической топологии / А.Т. Фоменко, Д.Б. Фукс. - М.: Наука, 1989.
- Демидов, Е.Е. Нелинейный корреляционный анализ / Е.Е. Демидов, Ю.В. Даревская, О.А. Моренков, А.А. Товчигречко // Обозрение прикладной и промышленной математики. - 1999. - Том 6, Вып. 1. - С. 4-57.
- Chazal, F. A sampling theory for compact sets in Euclidean space / F. Chazal, D. Cohen-Steiner, A. Lieutier // Discete and Computational Geometry. - 2009. - Vol. 41, Issue 3. - P. 461-479. -
- DOI: 10.1007/s00454-009-9144-8
- Chazal, F. High-dimensional topological data analysis. Handbook of discrete and computational geometry. - Boca Raton, FL: CRC Press, 2017. -
- ISBN: 978-1-4987-1139-5
- Ribeiro, M. "Why should i trust you?" Explaining the predictions of any classifier [Electronical Resource] / M. Ribeiro, S. Singh, C. Guestrin. - URL: https://arxiv.org/abs/1602.04938 (request date 30.10.2018).
- Katok A. Introduction to modern topology and geometry / A. Katok, A. Sossinsky [Electronical Resource]. - URL: http://www.personal.psu.edu/axk29/TOPOLOGY/ (request date 30.10.2018).
- Erickson J. CS 598: Computational topology. Spring 2013 [Electronical Resource]. - URL: http://jeffe.cs.illinois.edu/teaching/comptop/index.html (request date 30.10.2018).
- The MNIST database of handwritten digits [Electronical Resource]. - URL: http://yann.lecun.com/exdb/mnist/ (request date 30.10.2018).
- Hennig, C. Dissolution point and isolation robustness: Robustness criteria for general cluster analysis methods / C. Hennig // Journal of Multivariate Analysis. - 2008. - Vol. 99, Issue 6. - P. 1154-1176. -
- DOI: 10.1016/j.jmva.2007.07.002


