Распознавание изображений на основе вероятностной нейронной сети с проверкой однородности

Большинство исследований в области автоматического распознавания изображений (АРИ) [1] сосредоточены на повышении точности, надёжности и вычислительной эффективности существующих решений за счёт применения новых признаков [2, 3], мер близости [4], коллективных решений [5], приближённых методов ближайшего соседа [6] и пр. При этом достаточно часто применяется универсальный статистический подход [7, 8], согласно которому АРИ рассматривается как задача статистической классификации выборки признаков изображения [9]. В настоящее время наиболее часто используются непараметрические методы оценивания распределений классов, такие как нейросетевые методы и, в частности, вероятностные нейронные сети (probabilistic neural network, PNN) [10]. К сожалению, качество получаемого решения всё ещё недостаточно для большинства практически важных приложений (например, распознавание объектов по видео с вариативным освещением, ракурсом, размером и т.п. [11]).

В данной работе для решения задачи АРИ предлагается воспользоваться авторской модификацией PNN [12], основанной на редукции задачи классификации выборки к проверке статистической гипотезы о её однородности [13] с одной из обучающих выборок – множеством признаков эталонного изображения (а не к проверке гипотезы о распределении элементов входной выборки, как это принято в традиционной PNN). Для оценки распределения класса используется совместная выборка – объединение входной и обучающей выборок. В результате применение этой модификации приводит к следующим преимуществам [12] по сравнению с классическим подходом: более быстрая скорость сходимости к оптимальному решению, существенно меньшая зависимость точности классификации от параметров гауссовой ядерной функции Парзена–Розенблатта, симметрия получающейся меры близости.

Серьёзным недостатком аппарата PNN (и, соответственно, предложенной модификации) [10, 12] является требование к хранению и обработке всех элементов всех обучающих выборок (т.н. memorybased approach), что приводит к большим затратам при реализации этих алгоритмов и делает их физически нереализуемыми для сложных приложений, таких как АРИ. Поэтому актуальной становится задача синтеза критериев, эквивалентных при некоторых, достаточно общих ограничениях оптимальному решению [12], но не требующих хранения и сопоставления всех признаков.

Задача распознавания изображений

Пусть задано множество из L>1 полутоновых изображений X, = [ x ^[ ) J , I = 1, L , u = 1, U l , v = 1, V l . Здесь U_l – высота изображения, V_l – его ширина; x_u ^{( l} _v ⁾ – интенсивность точки изображения с координатами ( u,v ); l – номер эталона. Задача распознавания изображений состоит в том, чтобы отнести вновь поступающее (на вход) изображение X = [ -_uv ] (с высотой U и шириной V ) к одному из классов, заданных эталонами X_l . Каждый класс характеризуется тем, что принадлежащие ему объекты обладают некоторой общностью, сходством в характеристиках.

В распознавании образов общепринято [1, 11, 20] введение так называемого признакового пространства (feature set), когда исходные матрицы яркостей пикселей вначале преобразуются в набор простейших локальных признаков [ f u(vl) ] , где для каждой точки изображения (u, v) вычисляется признак fV) = f (x. , u, v), и = ш, v = 1V.

Здесь f (∙) – некая функция, выбираемая исследователем заранее. Аналогично строится набор признаков [ f uv ] входного изображения X . В ранних работах в качестве признаков использовались сами отсчёты яркости [21]

f ( X , и , v ) = x ( V) .                                     (1)

В настоящее время достаточно часто стали применяться текстурные признаки [2, 3]. Например, хорошие результаты показало направление градиента яркости [3, 22, 23]

x (¹)       - x ( ¹ )

• " = arctg              .                             (2)

• ^- u + 1, v ^- u , v + 1

Этот признак характеризуется весьма желательным для многих практических приложений АРИ свойством [1, 2] – инвариантностью к интенсивности освещения. Далее обычно [1–3] на основе локальных признаков вида (1) или (2) путём функциональных преобразований (нормировки, масштабирования и т.п.) и фильтрации (выделения регионов интереса, region of interest (ROI)) [2] формируются более сложные векторы признаков, которые и используются для решения АРИ. Тем не менее в дальнейшем во избежание новых обозначений мы будем предполагать, что имеем дело с простейшими признаками, в которых размерность набора признаков совпадает с размерностью анализируемых изображений.

Для распознавания в условиях небольшого числа эталонов для каждого класса обычно применяют правило ближайшего соседа [20]. Исследователь выбирает некоторую меру близости р ( X , X₁ ) и принимает решение в пользу класса X_l* такого, что

• 1    * = arg min р ( X , X₁ ) .                              (3)

• 1 = 1, L

Для определения расстояния р (X, Xl) можно сопоставлять непосредственно сами значения призна- ков. К сожалению, этот подход не всегда позволяет получить удовлетворительные результаты [23], что связано с известной [1] вариативностью зрительных образов, которая не может быть устранена стандартными алгоритмами очистки изображения от шума. Поэтому более перспективным представляется подход [2, 3], в котором каждому изображению ставится в соответствие гистограмма его признаков, при этом дальнейшее решение АРИ (3) основывается на сопоставлении гистограмм [3, 22]. Для построения гистограммы признака его область определения [ fmin; fmax ] разобьём на N отрезков одинакового размера

-

Д f = max n mm , Тогда элементы гистограммы H ^{( 1} ) = [ h ¹ ) , h 2 ¹ ) ^ ,h N' ) ] могут быть вычислены стандартным способом [9, 20]. Аналогично вычисляется и гистограмма H = [ h 1 ,..., h_N ] изображения X . Решение принимается по критерию (3) близости гистограмм, например, в традиционной метрике L ₂ Евклида [2]

N ₂

р 2 ( X , X1 ) = ^ ( h - h\¹ ) ) . (4) i = 1

Заметим, что зачастую на этапе предварительной обработки после детектирования распознаваемых объектов (например, лиц на фотографиях [15]) их изображения разбиваются на несколько (возможно, пересекающихся) частей [2, 5, 16], а затем решение принимается по принципу минимума суммы рассогласований между соответствующими частями. Однако для упрощения дальнейших выкладок мы будем предполагать, что гистограмма признака вычисляется для всего изображения.

К сожалению, критерий (4) не всегда демонстрирует удовлетворительное качество АРИ [5, 11, 23]. Повышение точности распознавания большинство исследователей связывают с применением статистического подхода, который и будет рассмотрен в следующем разделе.

Распознавание изображений на основе вероятностных нейронных сетей

Для применения статистического подхода [7, 9] предполагаем, что признаки f _u ⁽ _v ^{l )} в одном фрагменте изображения являются реализацией некой случайной величины F_l . Как сказано выше, далее для упрощения формул мы предполагаем, что анализируется не отдельный фрагмент, а всё изображение целиком.

В таком случае задача сводится к проверке L гипотез о распределении Р ₁ , 1 = 1, L , изображения на входе P :

^ : P = P 1 . (5)

Оптимальное решение при условии полной априорной неопределённости (равной априорной вероятности появления каждого класса) тогда даёт [7, 20] классический критерий максимального правдоподо- бия (условной вероятности P(X | Wl) принадлежности объекта X классу l )

P ( X| Wl ) ^ max .                            (6)

Далее, делая «наивное» предположение о независимости [5, 7] всех признаков изображений, используем ядерную оценку правдоподобия в (6) на основе классической PNN [10]

P ( ^Х «= Й Г^x

UVU l V l

ПП11 K ( l , л( I . ) ).

U = 1 V = 1 U . = 1 V . = 1

Здесь K ( ) – ядерная функция (например, гауссовское ядро Розенблатта–Парзена [10]). Использование оценки (7) наталкивается на классические проблемы PNN – невысокая скорость и завышенные требования к доступной памяти, обусловленные тем, что сохраняются все признаки всех эталонов. В результате практическая реализация критерия (6), (7) при L , U , V >>1 становится невозможной. Поэтому далее предположим, что случайные величины F l являются дискретными с конечным множеством из N значений { f ₁, …, f_N }. В этом случае выборки [ f_u ⁽ _v ^{l )}] могут быть полностью описаны гистограммой H ^{( l )} . В этом случае критерий (6), (7) может быть записан в виде

NN

П 1 Е K j h jl)

■ = 1 V j = 1

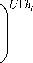
^ max. l

Здесь K j = K ( f_t , f -) – значения ядерной функции (предварительно вычисленные) между всевозможными парами значений признаков. Если для каждого эталона X_l и входного изображения X заранее вычислить свёртку его гистограммы с ядром

N hK) = E Kjh -), j=1

N hK» = 2Kjhj, ■ = 1,N, j=1

выполнить логарифмирование (9) и вычесть резуль-N тат из не зависящей от l величины ^ hi ln hK.i, то по-

• ■ = 1

лучим окончательное, основанное на аппарате PNN решение

Nh

V h ln—тут ^ min .

1 : 1 i     h KL;i         l

Заметим, что если здесь в качестве ядра используется дискретная дельта-функция, то h ^K' ’ = h i^(l ) , h K _; i = h i и выражение (10) будет эквивалентно правилу ближайшего соседа с достаточно часто использующимся в АРИ [5, 6] информационным рассогласованием Кульбака–Лейблера [24]

nh

Y; ln - у - ^ min.                          (11)

1z1 i h i^L )         i

Таким образом, оптимальное в байесовском смысле решение задачи статистической классификации изображений (5) принимается по критерию минимума решающей статистики (10) или (11). К сожалению, точность таких решений в практических приложениях АРИ особенно, с небольшим количество эталонов для каждого класса, оказывается иногда [11] даже ниже точности традиционного подхода (4). Поиск причин низкого качества оптимального решения (10) и составляет основную цель настоящей работы.

Вероятностная нейронная сеть с проверкой однородности в задаче распознавания изображений

Недостаточную точность решения (10) задачи статистической классификации (5) можно объяснить тем [13], что оно либо требует знания истинных распределений P _l , либо допускает, что правдоподобие оценивается (7) на основе обучающих выборок [ f_u ⁽ _v ^{l )} ] большого объёма по сравнению с входной выборкой [ f_uv ] . Последний факт подчёркивается и асимметрией решающего правила (10), (11).

Поэтому в настоящей работе для решения задачи АРИ воспользуемся известным альтернативным подходом [13], основанным на предложенной нами ранее для задачи классификации выборок независимых одинаково распределённых объектов PNN с проверкой однородности [12]. В настоящем разделе проведём адаптацию этой сети для случая дискретных признаков, выборки которых полностью определяются своими гистограммами.

Согласно известному подходу к распознаванию образов [13] с неизвестными заранее распределениями классов, задачу классификации следует сводить не к проверке гипотез о распределении вида (5), а к проверке статистической однородности обучающей и входной выборок. Тогда задача АРИ сводится к проверке простых гипотез W _l об однородности выборок признаков входного объекта и l -го эталона:

W_l : выборки признаков [ f_u ⁽ _v ^{l )} ] и [ f_uv ] однородны (одинаково распределены). (12) Её решение даёт классический байесовский подход минимума среднего риска [13], в рамках которого для случая полной априорной неопределённости ищется максимум (по возможным законам распределения входного объекта P ^* и эталонов P j , j = 1, L ) правдоподобия совместной выборки { X , X ₁ ,..., X_L } при справедливости гипотезы W l :

sup sup P ( { X , X 1 ,..., X_L }| W . ) ^ max,         (13)

• p * p * , j = 1, L                                                  ^l

где sup – верхняя граница по всевозможным значениям распределений. Предполагая независимость всех выборок (признаков входного и эталонных изображений), верхнюю границу в (13) запишем как

sup sup_ P ( { X , X 1

P * P * , j = 1 l

X L } W^ =

N

UV 2 hi ln i=1

h

K ; i

ɶ ɶ ( )

" K ; i ^{+ r} ' к ; i

+

= sup P ( X| W_Z ) - H sup P ( X j W l ) .

^P’                     j = i ^P j

где

N

+U/V, V h(i) ln ——K;'-.,. ^ min, i( )

'=1          hK; i + hK; i

Так как при справедливости W l выборки X j , j * l не зависят от W_l , то

LL

П supP (Xj|W)=supP (XiN-H supP (Xj) = j-I Pj                            Pi                        j-I Pj j * l

L supP(Xi|Wi)-n supP (X)

= лj=1 Pj_________ sup P (Xi)          .

C учётом этих двух равенств, разделив для симметрии (13) на не зависящий от l множитель

L supP (X )-П supP (X),

^P                 j = 1 ^P j

получаем следующий критерий supP (XW)-supP (XW) P*

--------------> max sup P (X)-sup P (Xi)

P*

Как известно [12, 13], верхняя граница в (14) достигается при равенстве распределений их максимально правдоподобным оценкам вида (7). Например, для вычисления верхней границы правдоподобия P ( X | W )

используется объединённая выборка { X , X } :

sup P (XI Wi) =-----1——х p        (UV+и vfV хП П 12 2k (х.,/.,.)+ u = 1 V=1 V U] =1 V] =1

U V

+ 22 к ( z . , z ( V ) ) l ,

U I = 1 . j = 1                            )

или, переходя к гистограммам выборок, supP (X Wi) =-----1—™х

p       (UV+и vU

N

N

N

UVhi

ɶ ( ) K ; i

ɶ hK;i

■ | M ' 2 K h ' UV i 2 K ij h j)

.

i = 1 V       j = 1

j = 1

Преобразуя последнее равенство, запишем его в упрощённой форме

N sup ^P ( X I W i ) = П P *                             i = 1

UVh

' Vh . + - Vh )

uv + и v,

.

Применяя к оптимальному правилу (14) оценки вида (15), запишем окончательное выражение для PNN с проверкой однородности [12] для дискретных конечных выборок

U V _h ( ) uv + и V, ;'

UV uv+uv,

^h K ; i ^.

Если предположить, что размеры всех изображений одинаковы, то последнее выражение для ядра – дискретной дельта-функции – сведётся к минимизации дивергенции Йенсена–Шеннона (Jensen-Shannon), с успехом применяющейся в разнообразных задачах АРИ [22, 25]

N

2 hi ln i=1

2hi hi + hi(i)

+

N

2 h(i)in i=1

2 h_i ^{( )} h i + h i^{(i )}

min .

I

Выражения (16), (17) содержат логарифмирование – потенциально «дорогую» (в смысле вычислительной сложности) операцию. Если требования к скорости вычислений являются критическими [6, 9], то зачастую применяют известную [24] аппроксимацию a a ² - b ²

логарифма ln— ®------. Соответственно, (16) мож- b 2ab

но приблизить критерием

N

UV 2 hKi i=1

N

+ u v 2

i = 1

_{h i} ( ) ( ) K ; i

,) 2 — hh_K. ,+ h l’)²)

;i             K;i       K;i h ^-hw        +

^H K ; i ^{+ r} KC ; i

( ) ² ɶ ɶ ( ) ²

¹¹K ; i )     (' K ; i +' K ; i ) I

hiic >  + hi к )

K ; i      K ; i

min. I

А (17), в свою очередь, после ряда упрощений [24] может быть аппроксимировано с помощью расстояния X ² [26]

₂ ( h i — h , "’ ) ²

Z! h i + h i^{(i )}

min .

I

Таким образом, если сформулировать задачу АРИ не в терминах статистической классификации (5), а свести её к проверке гипотез об однородности выборок признаков, то можно получить не только новые критерии (16), (18), но и при определённых допущениях известные выражения (17), (19), хорошо зарекомендовавшие себя в практических приложениях АРИ [25, 26].

Результаты экспериментальных исследований

Для проведения экспериментального исследования эффективности предложенного подхода (16), (18) рассмотрим задачу распознавания людей по фотографиям лиц [16, 19], являющуюся, как известно [15], одной из наиболее сложной в области АРИ. В качестве баз дан-

Лица на фотографиях выделялись с помощью библиотеки OpenCV. Далее выполнялась медианная фильтрация с размером окна 3×3 пикселя. Для вычисления рассогласований все изображения лиц предварительно разбивались на 16 (4×4) и 100 (10×10) фрагментов для гистограмм цвета (1) [9, 21, 27] и направлений градиента (2) [3, 22] соответственно. Эти значения показали в наших экспериментах наилучшую точность для рассматриваемых баз данных. Общее рассогласование между двумя фотографиями рассчитывалось как сумма рассогласований между соответствующими фрагментами, причём для учёта неоднородности ракурса и неточности детектирования лица каждая часть распознаваемого изображения сопоставлялась с фрагментами эталонного изображения из окрестности 3×3 (более подробно эта процедура и её преимущества описаны в работе [16]).

В ходе эксперимента сопоставлялась зависимость средней точности АРИ от числа n_p фотографий каждого человека, которые помещаются во множество эталонов. Точность оценивалась следующим образом. Для каждого класса (отдельного человека) наугад выбиралось n p фотографий, которые помещались в обучающую выборку. Остальные фотографии формировали тестовое множество. Итоговая точность оценивалась как средняя точность после 20 таких экспериментов.

Исследовались предложенные критерии (16), (18) с их частными случаями (17), (19), а также традиционное расстояние Евклида (4) и оптимальные критерии на основе PNN (10), (11). Для PNN (10) и её модификации (16), (18) использовалось гауссовское ядро Парзе-на–Розенблатта с параметром сглаживания (среднеквадратичным отклонением) g = 0,577. Каждый критерий был реализован в нейросетевом (многопоточном) варианте с 8 потоками в среде Microsoft Visual C++ 2010 Express Edition на современном ноутбуке (четырёхядерный процессор Intel Core i7-2630QM, тактовая частота 2 ГГц, объём ОЗУ 6 Гб).

Все результаты – оценки вероятности ошибки АРИ для сопоставления гистограмм яркости (1) и базы данных AT&T сведены в табл. 1. Здесь полужирным шрифтом выделены лучшие результаты (наименьшая вероятность ошибки) по столбцу (для фиксированного n p ).

Наши эксперименты (табл. 1 и 2) показали известный факт: из двух рассматриваемых признаковых пространств гистограммы направлений градиента существенно превосходят по качеству АРИ гистограммы цвета. Поэтому далее для базы данных JAFFE рассмотрим только более совершенные признаки. Результаты приведены в табл. 3.

n p Критерий	1	2	3	4
L 2 (4)	33,1%	18,5%	10,9%	7,3%
PNN (10)	29,1%	16,2%	9,6%	6,0%
Кульбака– Лейблера (11)	30,9%	17,4%	10,2%	6,6%
Йенсена–Шеннона (17)	26,0%	14,3%	7,6%	4,6%
Хи-квадрат (19)	26,2%	14,0%	7,5%	4,6%
PNN с проверкой однородности (16)	26,0%	14,2%	7,7%	4,6%
Приближённое выражение для PNN с проверкой однородности (18)	25,8%	14,0%	7,7%	4,8%

n p Критерий	1	2	3	4
L 2 (4)	23,5%	11,6%	7,1%	3,4%
PNN (10)	21,9%	10,3%	6,0%	2,8%
Кульбака–Лейблера (11)	24,5%	12,5%	7,5%	3,8%
Йенсена–Шеннона (17)	21,1%	9,7%	5,3%	2,3%
Хи-квадрат (19)	21,0%	9,6%	5,3%	2,2%
PNN с проверкой однородности (16)	20,7%	9,5%	5,2%	2,2%
Приближённое выражение для PNN с проверкой однородности (18)	20,5%	9,5%	5,3%	2,4%

Таблица 3. Вероятность ошибки АРИ для гистограмм направлений градиента и JAFFE

n p Критерий	1	2	3	4
L 2 (4)	17,4%	8,3%	5,9%	3,6%
PNN (10)	13,6%	5,3%	4,1%	2,0%
Кульбака–Лейблера (11)	16,3%	6,7%	4,6%	2,5%
Йенсена–Шеннона (17)	12,8%	5,3%	4,2%	2,4%
Хи-квадрат (19)	12,9%	5,1%	4,1%	2,3%
PNN с проверкой однородности (16)	11,5%	4,6%	3,5%	1,9%
Приближённое выражение для PNN с проверкой однородности (18)	11,2%	4,7%	3,75%	1,9%

Наконец, в табл. 4 показано среднее время вычисления рассогласования (в микросекундах) между двумя изображениями (для нейросетевой многопоточной реализации).

Таблица 4. Среднее время вычисления меры близости (в мкс)

	Время (мкс)
Критерий	Гистограмма цвета	Гистограмма направлений градиента
L 2 (4)	4	6
PNN (10) / Кульбака– Лейблера (11)	14	40
Йенсена–Шеннона (17)	24	69
Хи-квадрат (19)	6	16
PNN с проверкой однородности (16)	34	101
Приближённое выражение для PNN с проверкой однородности (18)	10	27

Здесь время распознавания для направлений градиентов превосходит аналогичный показатель для гистограмм цвета из-за различий в размере сетки, на которые разбиваются фотографии. Однако пропорция между отдельными критериями остаётся приблизительно одинаковой (за исключением метрики Евклида (4), для которой время классификации является чересчур малым для точного измерения).

По результатам проведённых экспериментов (табл. 1–4) можно сделать следующие выводы. Во-первых, точность классификации критериев (16)–(19), основанных на проверке статистической однородности выборок (12), существенно превосходит как детерминированный подход (4), так и оптимальные решения задачи статистической классификации (5), воплощённые в PNN (10) и принципе минимума информационного рассогласования Кульбака–Лейблера (11). Во-вторых, применение приближённых равенств (18), (19) сопровождается не только резким повышением вычислительной эффективности (что неудивительно, см. таблица 4), но и зачастую понижением вероятности ошибки по сравнению с оригинальными критериями (16) и (17) соответственно. В-третьих, качество АРИ для предложенных критериев (16) и (18) с гауссовским ядром Парзена–Розенблатта оказалась в среднем выше по сравнению с широко использующимися [25, 26] дивергенцией Йенсена–Шеннона и расстоянием хи-квадрат. Таким образом, можно сделать основной вывод: использование подхода, согласно которому задача АРИ сводится к статистической проверке однородности (11), позволяет объяснить недостаточное качество оптимальных решений (10), (11) задачи классификации (5).

Заключение

В настоящей работе предложена модификация (16) вероятностной нейронной сети с проверкой однородности [12] для случая распознавания выборок дискретных объектов, полностью описываемых своими гистограммами. Эта модификация сделала возможной практическую реализацию в режиме реального времени (см. табл. 4) оптимального решения (13) для задач с большим числом признаков. Действительно, в случае, если множество значений каждо- го признака является конечным, то появляется возможность сопоставлять не сами признаки (7), а их гистограммы (8), тем самым снижая вычислительную сложность в UVU lVl /N2 раз (ср., например, (7) и (8)). При этом для произвольной ядерной функции объём оперативной памяти, необходимый для реализации критериев (16), (18), лишь в 2 раза превышает аналогичный показатель для традиционных критериев, основанных на сравнении гистограмм, таких как (4), (17) и (19), за счёт сохранения для каждого изображения свёртки его гистограммы с ядром (9). Для большинства приложений это более чем умеренная плата за повышение точности распознавания (см. табл. 2, 3).

Отметим ещё одно потенциальное преимущество [12] использования предложенного подхода (16), (18) модификации (6) в задаче АРИ по сравнению с традиционными реализациями оптимального критерия (10), (11) – синтезированное выражение (16) в отличие от (10) является симметричным (с точностью до множителей UV и U_lV_l , характеризующих объём выборки). Действительно, в задаче проверки однородности (12) выборки считаются равнозначными. А при статистической классификации (5) в PNN (10) наблюдается асимметрия между распределением, заданным обучающей выборкой, и распределением входного объекта. Это обстоятельство может служить дополнительным обоснованием для выбора критерия (16), (18), т.к. симметрия является желательным свойством [20] рассогласования между объектами для многих алгоритмов распознавания образов (таких как кластеризация).

Таким образом, в настоящей работе выполнено строгое теоретико-вероятностное обоснование наблюдаемой большинством исследователей АРИ недостаточной точности максимально правдоподобного решения, основанного на принципе минимума информационного рассогласования Кульбака–Лейблера (11), по сравнению с расстоянием хи-квадрат (19) или дивергенцией Йенсена–Шеннона (17). Обычно [5, 11] неоп-тимальность выражений (10), (11) объясняют тем, что предположение о статистической независимости признаков, лежащее в основе классификатора Байеса, является слишком «наивным» в задаче АРИ. Однако представленная работа наглядно показала, что причина может объясняться и тем, что задачи распознавания образов следует сводить не к статистической классификации (5), а к проверке однородности признаков входного и эталонного изображений (12).

Исследование осуществлено в рамках Программы «Научный фонд НИУ ВШЭ» в 2013-2014 гг., проект № 12-01-0003.