Распознавание изображений пространственных точечных объектов

Одним из основных факторов, обеспечивающих успешное решение задачи распознавания изображений, расположенных в пространстве точечных объектов, является наличие их адекватных математических моделей и применение такого математического аппарата, который позволяет получить требуемые результаты. Одним из подходов к обработке изображений трёхмерных точечных объектов является подход, основанный на применении теории кватернионного анализа [1], что, в свою очередь, было следствием развития методов теории комплекснозначного контурного анализа [2], применяемого для обработки плоских изображений. В этих работах применён так называемый сигнальных подход, когда изображение отождествляется с сигналом и все алгоритмы обработки строятся на основе методов единой теории обработки дискретных сигналов. С этих позиций в работах [1, 3] была обоснована целесообразность привлечения алгебры кватернионов для обработки точечных пространственных изображений. При этом были введены такие понятия, как кватернионный сигнал (КС) и мера схожести кватернионных сигналов. Также рассмотрены вопросы согласованной фильтрации, спектрального и корреляционного анализа КС.

Вместе с тем применение аппарата теории кватернионов для анализа изображений пространственных точечных объектов (ПТО) выявило неинвариантность меры схожести кватернионных сигналов к операции вращения точечного объекта в пространстве, что усложнило решение задачи распознавания подобных изображений.

В данной работе представлен подход к распознаванию изображений пространственных точечных объектов с неизвестными масштабом, параметрами вращений и порядком нумерации точек. Сопутствующими являются задача оценки параметров вращения и задача идентификации точечных отметок, которые решаются относительно эталонных ПТО.

Постановка задачи формулируется следующим образом. Имеется алфавит изображений эталонных ПТО 3 ={ £ (n)K)4 , где § (n) = (^i,1 (n), ^i,2 (n), ^i,3 (n)) - ко— ординаты n-й точки, заданных кватернионными сигналами

Qi={q i(n Ж-1, qi (n ) = q^ (n) i+qi2 (n) j+qi ,3 (n)k, где i = 0,1,..., L -1, L - объём алфавита; и наблюдаемый ПТО Е(c) = jc(c) (n)}0-1, заданный кватернионным сигналом Q(c) = {q(c) (m)}0-1, полученный на основе одного из эталонов путём масштабирования на масштабный коэффициент ц поворота вокруг произвольной оси, задаваемой векторным кватернионом r = ?1i + r2j + r3k на произвольный угол 2^ . Кроме того, порядок следования точек в Ξ(c) и, соответственно, кватернионов в Q (c) отличается от исходного. Необходимо вынести обоснованное решение о том, что Q (c) соответствует эталону с номером v, а также оценить параметры вращения.

Таким образом, КС Q ^{( c )} формируется следующим образом:

Q(c) ubQvb-1, 0 < v < L, тождественное равенство здесь означает, что в Q (c) изменён порядок нумерации кватернионов в сигнале.

Выравнивание ПТО и оценка параметров вращений

Для исключения влияния пространственного положения и масштабных размеров необходимо выполнить выравнивание изображений всех эталонных ПТО. Выполним центрирование и нормировку, тогда компоненты кватернионов, входящих в состав КС, задающих соответствующие эталонные ПТО, могут быть вычислены по формуле:

S wix (^i,i (n Hi,i)

q i , x ⁽ n ) = i =\ ₃                     ’ ^x = 1,2,3.

J SS ( ^ i , i ( j ) -I i , i ) 2 \ j =0 i =1

Для выравнивания по пространственному положению применим метод главных компонент [4].

Q i={q‘( n )}0" 1, qi(n) =(w ) qi ,1(n)+(wi )1,o qi ,2(n)+(w X.0 qi ,3(n); qi(nHwi X, qi ,1(nMwi )i,i qi ,2(n)+(w )2,i qi ,3(n); qi(n) =(wi )o,2 qi ,1(n)+(wi )i,2 qi 2(n)+(w L qi ,3(n) - цей вращений, соответствующей истинной оценке искомых параметров. Чтобы вынести обоснованное решение относительно номера искомой матрицы, необходи-( c )

мо применить данные операторы вращения к Q :

Q ⁽ - Mq ( m ) } 0"

Здесь ( w _i ) 0 , ( w _i ) 1 , ( w _i ) 2 - собственные вектора

ковариационных матриц вычисленных по координатам каждого из L нормированных и центрированных ПТО Q .

Аналогичные операции выполняются и с сигнальным КС Q ⁽ c ) , что, как было показано в [3], позволяет нам получить оценку параметров вращений по матрицам T , составленным из соответствующих собственных векторов c учётом возможных неоднозначностей оценок [6], т.е.

rq()( m)]

= J q2-)(m)

[ q3-)(m )j

5 -1

( c )

q1(m)

= k q 2 c ) ( m )

[ q 3 c)( m )J

5 -1

,

а также выполнить идентификацию точечных отметок

и определить, для какого из Q ^{( -} ) , i = 0,1,---,7 норми-

рованное скалярное произведение совмещённых и эталонного КС достигает своего максимума:

2 Ф ₁ = arccos

Ч, t i ⁾ 0,0 + 7X1 + ⁽ t i Х,2

P i ,1 =

^t 1,2

V

^t 2,1

2 sin ( 2 ф )

; P i ,i =

1'

;

m _i ax

[(Q(-),Q)    ]

norm

= max

5 -1

Е q( -) (n) q* (n)

_____ n =0 ___________________________

5 -1 I              |2 5 -1               A

Еq(i,(n) tiq*(n)

n =0              V n =0

^t 2,0

^t 0,2

2 sin ( 2 ф )

; p.

i ,3

^t 0,1

^t 1,0

2 sin ( 2 ф )

. (2)

Применив данные параметры вращений к сигнальному КС, получим набор КС, оптимально совмещённых с каждым из эталонов по критерию минимума расстояния или максимума скального произведения.

i = 0,1,..., 7.

Здесь Q ( ^- ) соответствует (Q ( ^- ) с переупорядоченными отсчётами [5].

Тогда в качестве матрицы для вычисления параметров вращений (оси вращения и угла) по формулам (1) и (2) может быть принята матрица

Устранение неоднозначности

Разложение по методу главных компонент не является единственным, так как возможно изменение знаков у компонент собственных векторов ковариационной матрицы, что приводит к изменению направлений главных компонент на противоположные [6]. Это свойство метода главных компонент называется вращательной неопределённостью и может привести к неправильной оценке параметров вращений и, соответственно, к неправильному совмещению изображений ПТО. Чтобы исключить подобные ошибки, был предложен следующий метод устранения данной неоднозначности.

Введём в рассмотрение так называемые поправочные матрицы вращений. Так как речь идёт о трёхмерном пространстве и у каждой из осей возможна неоднозначность только в выборе положительного или отрицательного направления, то таких матриц будет 2³ = 8 :

	" ( _ ! ) - mod 2	0	0 ]
т' = ‘ i	0	/ .. \( i divl)modi ( - 1 )	0	, (3)
	_ 0	0	( _ 1) ( i div 4 ) mod1
i = 0,1,-,7.

Тогда оценка параметров вращений может быть записана в виде 8 матриц следующего вида T = T Q T'T _{q (} c ) , только одна из которых является матри-

^T = ^T - Q ^TL T Q»,

где i _max – это номер поправочной матрицы, при которой достигнут максимум скалярного произведения как меры схожести КС [1, 2], описывающих изображения ПТО. Рассчитанная мера схожести затем используется при решении задачи распознавания.

Задача идентификации точечных отметок

Каждая точка ПТО, подвергающаяся воздействию координатного шума, представляющего собой независимую трёхмерную центрированную случайную величину, подчиняющуюся нормальному закону распределения, образует в пространстве геометрическое место точек или сферическую область D. Размер данной области определяется вероятностью попадания точки в область p_liXi , R ( n ) = q ( n ) + Z ( n ) , где q ( n ) - n -я точка ПТО, а Z ( n ) — шумовой вектор длиной Х = |Z ( n )| . Найдём совместную вероятность распределения координат зашумлённого вектора W 3 (| R\ , v , ф ) в сферической системе координат.

Согласно [8], если известны совместная плотность вероятности wn (x1,...,xn) случайных величин x1,..., xn и якобиан преобразования от случайных величин x1,..., xn к случайным величинам y1,..., yn dx 1

d ( x 1

^d ( У 1

xn ) =

У п )

a y i

...

^d x n 8y 1

d x 1 ^d У п

...

^d x n ^d У п

где Ф

X

1 f "^2 |Z|

,— I e ^{2 q} d —. Пользуясь функцией Ла-

V 2 п 0 Q

1 x z ²

пласа Ф ( x ) = ,— I e ²d z и зная величины X и q , J7-JT * М ^п 0

то распределение чин равно

W n ( У 1 >-> У 2 ) =

преобразованных случайных вели-

^d ( ^x 1 k ,-, ^xnk ) ^d ( У 1 ,..., У п )

■ w n ( x 1 >-> x n ) ^,

где x_ik – k -я ветвь обратного преобразования

( i = 1,..., n ) .

Тогда для нашего случая будем иметь

W (iw-x

Q (2n)

( sjn ( v ) cos ( ф ) - q_A ) 2 + ( sjn ( v ) s^n ( ф ) - q 2 )² + ( cos ( v ) - q 3 ) 2

-I ^Л 1                           273

x e                      ^{2 q}

Найдём одномерное распределение модуля шумового вектора ζ , подчиняющееся трёхмерному нор-

мальному распределению со среднеквадратическим отклонением q и нулевым математическим ожиданием:

л 2п                        1г12 F-^t

W (|Z|) = J J W 3 ( v , Ф ,I Z ) d ф d v =         e ^{2 Q} 2 ,

00                         ^Q 4"

т.е.

^(И) -^ e                     (7)

Последнее выражение называется распределением Максвелла [8] или сферическим распределением (рассеиванием).

Известно, что если случайная величина X задана плотностью распределения f ( x ) , то вероятность того, что X примет значение, принадлежащее интервалу ( 0, в ) , такова:

р

P ( 0 < X

) = j f ( x ) d x .                     (8)

Так как модуль шумового вектора описывается распределением Максвелла (7), то выражение (8) примет вид

X                          X |_z|² ГТ 1 Z|²

P ( ⁰ <|;|<^x ) = j W (|c| ) d c|= j Я J- e -’^dIZ-

0                0 ^Q V ⁿ

Преобразуя последнее выражение, получим

P ( 0 <|z|) = 2

Ф

x

Q

X 1

Q 72Л

X ²

2 q ²

можно определить величину вероятности P ( 0 <|z|). Так как для вычисления функции ф(x) используют специальные таблицы (неопределённый интеграл в этой функции не может быть выражен через элементарные функции и вычисляется с применением численных методов), то, соответственно, для функции

W ( x ) =

1 - xX

Ф ( x ) - x ,— e ² v2n

тоже можно составить подобную таблицу.

Величина X выбирается в соответствии с заданным значением вероятности, с которой зашумлённая точка должна находиться в пределах области D . Для определения величины X при заданном P ( 0 <|z|) = p_iiaia и известной величине СКО q необходимо:

• 1)    определить величину x , при которой W ( x ) близко к величине P ( 0 < |z| < X ) ;

• 2)    умножить найденную величину x на q .

Используя формулу для расстояния между точками исходного и совмещённого зашумлённого объектов и зная величину X , можно рассчитать матрицу F :

F = { ^f [ m , ^п ] } = ^X 2 ^- ^ ( p_t ( ^п ) ^- q . ( m ) ) ,         ⁽¹¹⁾

i =1

где m = 0,1,..., 5 - 1 - номер точки эталона, п = 0,1,..., 5 - 1 - номер точки (зашумлённой) сигнального КС после выполнения совмещения.

Результаты вычислений по формуле (11) можно

свести в матрицу

Г f ( 0.0 )       f ( ^0,1 )     ...     f ( 0, 5 - 1 ) ^

F = f ( 1,0 )       f ( 1,1 )     ...     f ( 1, 5 - 1 )

...                       ...             ...                 ...

_v f ( k - 1,0 ) f ( k - 1,1 ) ... f ( k - 1, 5 - 1 )_?

Из всех элементов матрицы работаем только с теми, которые удовлетворяют условию f ( m , n ) >  0 , т.е. рассматриваем элементы, попадающие в стробы (области D).

Затем находим максимальный элемент во всей матрице F , запоминаем номер строки и столбца – m ₁ и n ₁ , после этого вычёркиваем из матрицы столбец с номером n ₁ и строку с номером m ₁ и т.д. Когда будут вычеркнуты все элементы матрицы либо когда останутся только отрицательные элементы, т.е. элементы,

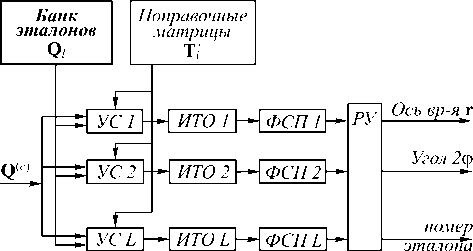
не попадающие ни в один из стробов, процесс идентификации закончен. В итоге мы получаем два набора чисел, содержащих номера векторов эталонного и сигнального КС, сопоставленных друг с другом

N = {”J1,s- M = {mi}1,s- , причём s- - число успешно идентифицированных отметок.

Заметим, что изначально точки, входящие в состав сигнального ПТО, могут быть пронумерованы в произвольном порядке.

Решение задачи распознавания

Решение задачи идентификации точечных отметок позволяет применить для расчёта меры схожести между изображениями пространственных точечных объектов величину скалярного произведения кватернионных сигналов. Данное обстоятельство позволяет реализовать устройство распознавания изображений пространственных точечных объектов (рис. 2).

принадлежности к l -му классу, найденная по его первым s' точкам, равна

P ( Q l Iq^s ')) =

= P ( q ⁽ i ^max ) ( s ') I Q l ) ■ P ( Q l I q ⁽ i ^max ) ( s '-1))

^2 P ( q (i max ) ( s - ) I Q , ) ■ P ( Q j I q °™) ( s ‘- 1)) j =o

Здесь P ( Q l I q ⁽ i ^{max )})( s '- 1)) - апостериорная вероятность принадлежности ПГТО к l -му классу, набранная по ( s' - 1) его первым точкам, принимаемая в качестве априорной вероятности для s' -го шага.

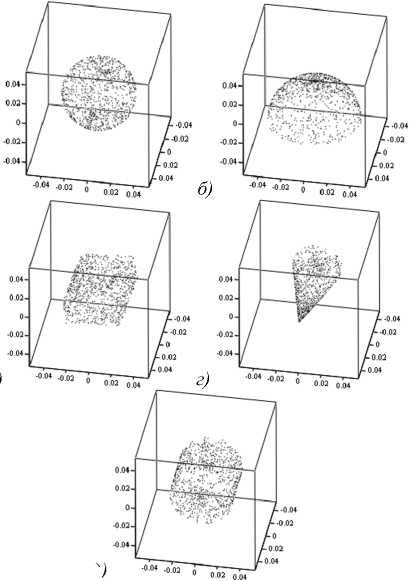
Моделирование работы алгоритма

В качестве алфавита эталонных пространственных точечных объектов были сгенерированы трёхмерные точечные сцены геометрических объектов (рис. 2): сфера, полусфера, параллелепипед, конус, цилиндр (количество точек в каждой сцене – 1000).

Рис. 1. Устройство распознавания ПГТО с неизвестным углом поворота и неизвестной нумерацией точек в объекте

Здесь введены следующие обозначения: УС – устройство совмещения, ИТО – идентификатор точечных отметок, ФСП – формирователь скалярного произведения, РУ – решающее устройство.

Кроме того, при известном распределении вероятностей координатного шума возможно применение байесовского алгоритма. Каждой точке ПГТО по величине отклонения от соответствующей точки эталона можно поставить в соответствие условную вероятность P ( q ^{( i max )} ( n ) / Q _l ) . В результате можно сформировать матрицу P условных вероятностей принад-

лежности точек точечного объекта

Q i , l = 0,1, ^ , L - 1:

классам

а)

д)

Рис. 2. Примеры сцен с изображениями пространственных точечных объектов: сфера, полусфера, параллелепипед, конус, цилиндр (количество точек N = 1000)

P = {p (q(imax)(n) /Ql)}

n =0.. s --1, l =0..: L -1

.

При наличии матрицы P в качестве меры схожести ПГТО Q ^{( i max )} и Q _l удобно использовать значения апостериорной вероятности P ( Q _l / Q ^{( i max )}) принадлежности ПГТО Q ^{( i max )} к l -му классу:

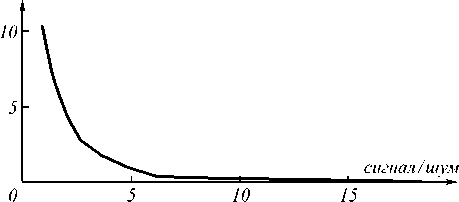
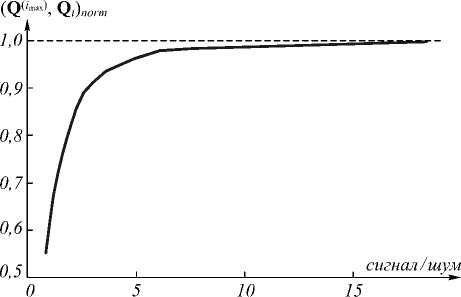
На данных сценах была выполнена апробация предложенных алгоритмов и рассчитаны характеристики оценки точности определения параметров вращения в виде зависимости ошибки оценки угла поворота от отношения сигнал/шум при неизвестной нумерации точечных отметок в объекте (рис. 3); и оценки величины меры схожести между эталонными и совмещённым объектом от отношения сигнал/шум (рис. 4).

q ⁽ i max ) _e q l при p ( q l / q ⁽ i max ))— — max.       (14)

Данная вероятность пошагово определяется с помощью формулы Байеса. Апостериорная вероятность

|2ф-2ф|

Рис. 3. Зависимость ошибки оценки угла поворота от отношения сигнал / шум

По результатам анализа полученных характеристик можно отметить, что предложенные алгоритмы работоспособны и позволяют решать задачу оценки параметров вращений изображений пространственных точечных объектов при неизвестной нумерации точечных объектов, а также задачу распознавания.

Рис. 4. Зависимость величины меры схожести между эталонным и совмещённым объектом от отношения сигнал/шум, при l = 0

Заключение

Использование метода главных компонент, основанного на свойствах характеристических векторов ковариационной матрицы, рассчитанной по координатам точек пространственного точечного объекта, позволяет получить оценку параметров вращений. Достоинством является то, что при этом порядок следования точек в исходном и повёрнутом объектах может не совпадать.

Приведён метод устранения неоднозначности, возникающей при оценке параметров вращений.

Представлен алгоритм идентификации (сопоставления) точек совмещённого (зашумлённого) и исходного (эталонного) пространственных точечных объектов, позволяющий применять для решения задачи распознавания таких изображений методы теории дискретного кватернионного анализа и, в частности, ввести меру схожести изображений ПТО, описанных с помощью кватернионных сигналов в виде скалярного произведения в гиперкомплексном пространстве.

Предложен метод распознавания изображений пространственных точечных объектов на основе последовательной стратегии Байеса.

Выполнен расчёт характеристик в виде зависимости ошибки оценки угла поворота от отношения сиг-нал/шум при неизвестной нумерации точечных отме- ток в объекте; и оценки величины меры схожести между эталонными и совмещённым объектом от отношения сигнал/шум.