Распознавание элементов сцены по её неполному изображению

Работа по анализу, исследованию и алгоритмизации методов моделирования сцены для имплантации виртуальных образов уже ни один год ведется в России и западных странах (BrandBrigade1, Sportvision Inc.2, Hego Group3, Orad Hi-Tec Systems4), но чаще всего это коммерческие частные разработки, защищенные патентами и договорами о неразглашении. Пример работы одной из коммерческих программ приведен на рисунке 1. Имеющиеся разработки в данной области не содержат описания работы алгоритмов или частей алгоритмов в открытом доступе. В связи с этим, исследование и разработка методов моделирования сцен является актуальной и целесообразной задачей.

Рис. 1. Работы коммерческой программы по имплантации виртуальных образов AKI Virtual Football компании Hego Group на примере спортивных мероприятий

• 1.    Логико-геометрический анализ сцены

Степень разработанности проблемы является недостаточной. Применительно к имплантации виртуальной рекламы при футбольных телетрансляциях имеется патент («Method and apparatus for implanting images into a video sequence» – Patent Numbers: P-783-IL in , P-783-SG in , P-783-AU in ) и работы ( «A new approach to image processing» Рубчинский А.А), не содержащие описания нескольких этапов, включая важный этап логического анализа сцены с отдельными распознанными объектами.

При решении проблем с логическим анализом сцены предполагается применить методы системного анализа, и методы искусственного интеллекта, относящиеся к правилам вывода, хорновские формулы. При этом появляется необходимость существенной модификации и разработки новых вариантов правил вывода, учитывающих геометрическую специфику объектов. В данном случае из проблемы моделирования сцены выделяются задачи логико-геометрического типа.

В рассматриваемом случае сцена предполагается известной и задача состоит в распознавании элементов сцены, расположенных (возможно, частично) на участке сцены, получаемом с помощью камеры. В данном случае под распознаванием понимается установление взаимно-однозначного соответствия между отрезками линий, имеющихся на кадре, и отдельными элементами сцены, являющиеся известными заранее линиями.

В статье рассматривается частная задача логико-геометрического распознавания сцены – распознаваний линий на плоскости. Для примера была выбрана задача распознавания линий разметки на футбольном поле. В нашем случае мы заранее имеем полную картину сцены, нашей задачей является распознавание линий сцены отдельного участка, захваченного камерой, общим решением данной задачи является применение логических условий расположения линий в пространстве относительно друг друга.

Прежде чем перейти к описанию используемых принципов решения данной задачи введём некоторые понятия и определения.

Для решения поставленной задачи, мы будем использовать исчисления предикатов. По аналогии с «Миром блоков», необходимо ввести понятие «Мир линий». «Мир линий» – это записанное с помощью исчисление предикатов отношение между линиями и группами линий. Мир линий состоит из отрезков линий разной длины, находящихся в определенных отношениях относительно друг друга (пересечение, параллельность и т.д.).

Для решения данной задачи была написана программа на языке высокого уровня, стоит отдельно отметить тот факт, что входные данные для программы (параметры мира линий) не были заранее сгруппированы, входные данные могли вводиться в любой последовательности.

Разработанная программа предназначена для распознавания линий разметки футбольного поля. Программа распознает линии разметки для случаев с уже известной стороной поля, программа не обладает универсальностью, но позволяет распознавать линии разметки в приведенных ниже случаях. Работа программы в первую очередь основана на определении среди уравнений прямых (входные данные) линии разметки. Затем определяются (если заданы) боковые линии (ближняя боковая, дальняя боковая). В зависимости от количества заданных линий определяются точки пересечения: в программе имеют место пересечения вида начало-начало, конец-начало (начало-конец) и конец-конец. Определение точек начало и конца отрезков основано на заранее известных данных о стороне поля.

Приведем пример распознавания линий для данной задачи (первоначальные кадры представлены на рисунках 2, 7, 10):

Рис. 2. Первоначальный кадр

Рис. 3. Первоначальный кадр для первого случая

Рис. 4. Пример нахождения линии ворот

Рис. 5. Расшифровка номеров линий для первого случая

Поясним, как работает распознающий алгоритм. На первоначальном кадре (рис. 3), имеется простой геометрический факт: все линии, идущие ВДОЛЬ поля (боковые линии поля, линии штрафной и линии вратарской) пересекаются с линией ворот только концами. Напомним, что концом в данном случае названа точка на линии с максимальной координатой по оси х-ов (в системе координат, привязанной к левому верхнему углу изображения), началом названа точка на линии с минимальной координатой по оси х -ов и что все концы (и начала) линий ИЗВЕСТНЫ, как и их уравнения.

Поэтому для каждой из линий, идущих ПОПЕРЁК поля, проверяем условия нахождения на ней всех концов заданных линий, идущих ВДОЛЬ поля (в рамках данного кадра). Если существует линия на которой находятся более одного конца, то это и есть линия ворот (см. рис. 4).

Введём в рассмотрение предикат «belong(α,β)» , принимающий значение «истина», если точка α лежит на линии β , и «ложь» в противном случае. С помощью предиката «belong(α,β)» находим линию ворот (если она есть на кадре) или определяем её отсутствие.

Рассмотрим столь же простые соображения, связанные с боковой линией штрафной. Линия (идущая вдоль поля) является боковой линией штрафной, если:

• a)    её конец совпадает с концом (или началом) линии ворот, или

• b)    на рисунке есть точка пересечения боковой линии поля и линии ворот и данная линия является ближайшей к боковой линии, или

• c)    точка пересечения данной линии с линией ворот находится левее (у неё меньше координата х ) или правее (у неё больше координата х ), чем точка пересечения какой-либо другой линии с лицевой, которая левее штанги ворот, и т.д.

Все условия записываются в терминах двух предикатов – упомянутого belong(α,β) и cross (α,β) (пересечения линий α и β ).

Следует также отметить, что изначально известна сторона поля кадра, в нашем случае (рис. 3) – правая.

Рассмотрим пример (рис. 5, 8, 11). С помощью приведённых выше простых условий мы можем определить линию ворот ( y ₁ ) и дальнюю боковую линию ( y ₂ ). После этого используя предикат belong(α,β) , находим оставшиеся линии, идущие ПОПЕРЁК, концы которых лежат на линии ворот.

Имея данные о наличии среди исходных данных боковой линии (дальней или ближней) и точно зная количество линий, концы которых лежат на линии ворот, мы можем сделать вывод о том, какие это линии. Например, для нашего случае (рис. 5), мы имеем 3 пересечения с линией ворот. Одно из пересечений мы уже определили выше – дальняя линия боковой, следовательно, два оставшихся пересечения легко определяются, а линии распознаются как дальняя линия вратарской и дальняя линия штрафной. Зная, что геометрически одна прямая лежит выше другой, а следовательно коэффициент b ( y = k • x + b ) дальней линии штрафной будет больше коэффициента b для дальней линии ворот. Затем, среди оставшихся линий идущих ПОПЕРЁК, находим те, которые пересекаются с дальней линией штрафной и дальней линией вратарской, это передняя линия штрафной и передняя линия вратарской соответственно.

Приведем уравнения для описанного выше случая.

Имеем 6 линий. Уравнения для данных прямых:

у 1 = к 1 • x + m 1 ; y 2 = k 2 • x + m 2 ; y 3 = k 3 • x + m 3 ; y 4 = k 4 • x + m 4 ; y 5 = k 5 • x + m 5 ; y 6 = k 6 • x + m 6 .

Координаты начала и конца:

n ₁( x ₁₁, y ₁₁) и k ₁( x ₁₂, y ₁₂); n ₂( x ₂₁, y ₂₁) и k ₂( x ₂₂, y ₂₂); n ₃( x ₃₁, y ₃₁) и k ₃( x ₃₂, y ₃₂);

n ₄( x ₄₁, y ₄₁) и k ₄( x ₄₂, y ₄₂); n ₅( x ₅₁, y ₅₁) и k ₅( x ₅₂, y ₅₂); n ₆( x ₆₁, y ₆₁) и k ₆( x ₆₂, y ₆₂).

Сторона поля: sight (right) – сторона поля правая.

Присутствует линия ворот. Количество пересечений вида начало-начало равно 2.

Запишем логические условия для распознавания линий разметки:

V y 1 V y 2 V y 3 V y 4 V y 5 V y ₆ number of (crossing ( y 1 , y 2 ) v crossing ( y ₁₅ y 3 ) v crossing ( y 1 , y 4 ) v crossing ( y 1 , y 5 ) v crossing ( y 1 , y 6 )) >  1 v number of (belong ( k 2 , y 1 ) v belong ( k 3 , y 1 ) v belong ( k 4 , y 1 ) v (belong ( k ₅, y 1 ) v (belong ( k ₆, y 1 )) >  1 ^ y 1 - линия ворот;

V y 1 V y ₂ V y ₃ V y ₄ V y ₅ V y ₆ ( n 1 ( x 11 , y 11 ) = k 2 ( x 22 , y 22 )) ^ y 2 - дальняя боковая линия;

∀ y ₁ ∀ y ₂ ∀ y ₃ ∀ y ₄ ∀ y ₅ ∀ y ₆ crossing ( y ₁, y ₃) ∨ crossing ( y ₁, y ₃) ∨ ( m ₃ >  m ₅) → y ₃ – дальняя линия штрафной; y ₅ – дальняя линия вратарской;

∀ y ₁ ∀ y ₂ ∀ y ₃ ∀ y ₄ ∀ y ₅ ∀ y ₆ ( n ₃( x ₃₁, y ₃₁) = n ₄( x ₄₁, y ₄₁)) ∨ ( n ₅( x ₅₁, y ₅₁) = n ₆( x ₆₁, y ₆₁)) → y ₄ – передняя линия штрафной, y ₆ – передняя линия вратарской.

Number of (function) – функция, проверяющая количество выполнений заданного условия.

Получившийся результат мы можем наблюдать на рисунке 6. Расшифровка цвета линий на рисунке представлена в таблице 1.

Рис. 6. Результат работы алгоритма по распознаванию линий для первого случая

Рис. 7. Первоначальный кадр для второго случая

Рис. 8. Расшифровка номеров линий для второго случая

Рассмотрим 2-ой случай, представленный на рис.7. Имеем 4 линии. Уравнения для данных прямых:

y 1 = k 1 • x + m ₁; y 2 = k 2 • x + m 2 ; y 3 = k 3 • x + m 3 ; y 4 = k 4 • x + m 4 .

Координаты начала и конца:

n₁(x₁₁,y₁₁) и k₁(x₁₂,y₁₂); n₂(x₂₁, y₂₁) и k₂(x₂₂,y₂₂); n₃(x₃₁,y₃₁) и k₃(x₃₂,y₃₂);

n₄ (x₄₁ , y₄₁ ) и k₄ (x₄₂ , y₄₂ ) .

Сторона поля: sight (right) – сторона поля правая. Отсутствует линия ворот. Количество пересечений вида конец-начало равно 2.

Запишем логические условия для распознавания линий разметки:

V y ₁ V y 2 V y 3 V y ₄( k ₁( x ₁₂, y ₁₂) = n ₂( x ₂₁, y ₂₁)) v ( m₁ >  m 3 ) v ( m 2 >  m 4 ) ^ y 1 - передняя линия вратарской; y ₂ – ближняя линия вратарской;

V y ₁ V y ₂ V y 3 V y ₄( k 3 ( x ₃₂, y ₃₂) = n ₄( x ₄₁, y ₄₁)) v ( m ₁ >  m 3 ) v ( m ₂ >  m ₄) ^ y 3 - передняя линия штрафной; y ₄ – ближняя линия штрафной.

Получившийся результат представлен на рисунке 9.

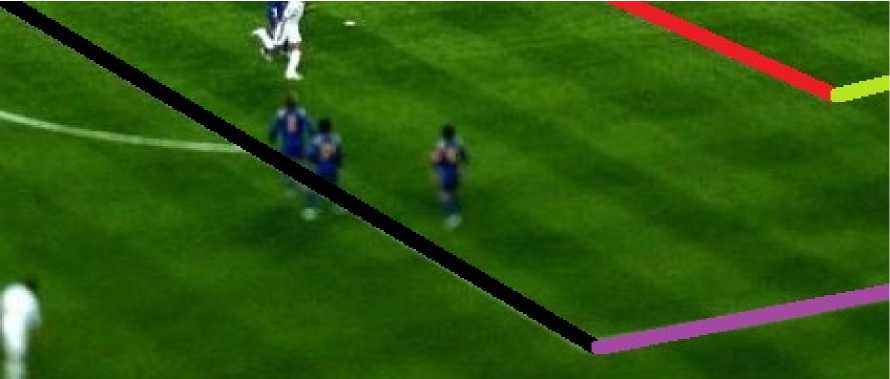
Рис. 9. Результат работы алгоритма по распознаванию линий для второго случая

Рис. 10. Первоначальный кадр для третьего случая

Рис. 11. Расшифровка номеров линий для третьего случая

Рассмотрим 3-ий случай (рис.10).

Имеем 3 линии. Уравнения для данных прямых:

y 1 = k 1 • x + m ₁; y 2 = k 2 • x + m 2 ; y 3 = k 3 • x + m 3 .

Координаты начала и конца:

n₁(x₁₁,y₁₁) и k₁(x₁₂,y₁₂) ; n₂(x₂₁, y₂₁) и k₂(x₂₂,y₂₂) ; n₃(x₃₁,y₃₁) и k₃(x₃₂,y₃₂) .

Сторона поля: sight (right) – сторона поля правая.

Отсутствует линия ворот.

Запишем логические условия для распознавания линий разметки:

V y 1 V y 2 V y 3 V y 4 V y 5 V y 6 number of (crossing ( y ₁, y 2 ) v crossing ( y ₁, y 3 ) v crossing ( y ₁, y 4 ) v crossing ( y ₁, y 5 ) v crossing ( y ₁, y 6 )) >  1 v number of (belong ( k 2 , y 1 ) v belong ( k 3 , y 1 ) v belong ( k 4 , y ₁) v (belong ( k 5 , y 1 ) v (belong ( k 6 , y 1 )) >  1 ^ y 1 - линия ворот;

V y ₁ V y 2 V y 3 number of (crossing ( y ₁, y 2 ) v crossing ( y ₁, y 3 )) >  1 v number of (belong ( k 2 , y ₁) v belong ( k 3 , y ₁) >  1 ^ y ₁ - линия ворот;

V y ₁ V y 2 V y 3 ( n ₁ ( x ₁₁, y ₁₁) = k 2 ( x 22 , y 22 )) ^ y 2 - дальняя боковая линия;

V y ₁ V y 2 V y 3 crossing ( y ₁, y 3 ) ^ y 3 - дальняя линия штрафной.

Number of (function) – функция, проверяющая количество выполнений заданного условия.

Получившийся результат представлен на рисунке 12.

Рис. 12. Результат работы алгоритма по распознаванию линий для третьего случая

Табл. 1. Расшифровка цветов линий на изображениях

Заключение

В данной статье рассматривается метод распознавания линий разметки. Работа в целом посвящена распознаванию линий не привязанных к конкретной задаче, это могут быть как спортивные, так и развлекательные мероприятия.

Существуют варианты, неподдающиеся точному распознаванию линий разметки полученным алгоритмом (например, случай представленный на рисунке 13). Случаи, подобные приведенному, встречаются не часто, чаще всего они присутствуют на изображениях, полученных при довольно большом масштабе. По примерным оценкам, за время матча, количество кадров, не поддающихся распознаванию, составляет 5-7% от общего объема материала.

Рис. 13. Первоначальный кадр для четвертого случая