Распознавание пахотных земель на основе многолетних спутниковых данных спектрорадиометра MODIS и локально-адаптивной классификации

Оценка состояния и динамики земного покрова на основе дистанционного зондирования со спутников часто сопряжена с необходимостью распознавания объектов поверхности на основе данных измерений отражённого или собственного излучения. Для этого, как правило, используются методы обучаемой или необучаемой классификации в пространстве признаков, обеспечивающих разделимость типов распознаваемых объектов [1]. При этом стандартные методы классификации, разработанные применительно к данным непространственной природы, не позволяют в явном виде учитывать географическую изменчивость значений признаков распознавания, вызванную особенностями физико-химических, морфологических и структурных свойств объектов, часто подчиняющихся, в случае растительного покрова, закономерностям широтной зональности и высотной поясности.

В этой связи эффективность применения стандартных методов классификации для обработки данных дистанционного зондирования, как правило, снижается с увеличением размеров изучаемой территории. Так, будучи достаточно эффективными при обработке данных на относительно небольшие участки, указанные методы становятся практически не применимыми на глобальном уровне без принятия мер по снижению изменчивости значений признаков распознавания. К числу наиболее часто используемых мер такого рода относится стратификация территории с выделением однородных по некоторым критериям регионов (страт), отличающихся сниженной вариабельностью значений признаков распознавания. Несмотря на то, что данный подход позволяет повысить точность классификации данных спутниковых наблюдений, его недостатком является возможная рассогласованность результатов на границах смежных страт.

Локально-адаптивный алгоритм глобального картографирования LAGMA (Locally-Adaptive Glo- bal Mapping Algorithm) [3] в силу наличия внутренне присущего ему механизма учёта географической изменчивости признаков распознавания свободен от указанных недостатков и может эффективно использоваться для классификации данных спутниковых наблюдений больших территорий.

Данные установленного на спутниках Terra и Aqua спектрорадиометра MODIS обеспечивают возможность картографирования растительного покрова на глобальном уровне и находят, в частности, широкое применение для мониторинга сельскохозяйственных земель [4,5].

Разработанный ранее в Институте космических исследований Российской академии наук (ИКИ РАН) метод выявления используемых пахотных земель на основе многолетних временных рядов данных MODIS нашёл применение при проведении Всероссийской сельскохозяйственной переписи 2006 года для получения независимой объективной информации [6]. Созданная на основе данного метода карта пахотных земель с пространственным разрешением 250 м вошла в состав информационного обеспечения Системы дистанционного мониторинга земель агропромышленного комплекса (СДМЗ АПК) [4].

Вместе с тем, дополнительные углубленные исследования показали наличие возможностей развития метода выявления пахотных земель по данным MODIS за счёт комбинированного использования набора информативных спектрально-временных признаков распознавания [7] и алгоритма локальноадаптивной классификации земного покрова [3].

Описанный в настоящей статье метод, основанный на использовании многолетних рядов данных MODIS и алгоритма LAGMA, обеспечивает возможность картографирования пахотных земель России с достаточной для решения многих практических задач точностью.

Алгоритм локально-адаптивной классификации

Использование методов обучаемой классификации, позволяющих относить объекты классам некоторого множества, заданным своими описаниями в выбранном пространстве признаков, в общем случае предполагает следующую последовательность логических шагов [1]:

• -    построение статистических описаний (сигнатур) классов в пространстве признаков на основе репрезентативной выборки характерных эталонов;

• -    классификация объектов на основе значений их признаков и полученных описаний классов.

Распознавание типов земного покрова по данным спутниковых наблюдений основано, как правило, на использовании в качестве признаков значений спектральной яркости объектов (или полученных на их основе различных производных признаков). Часто используемый статистический подход к классификации исходит из предположения нормального распределения значений признаков, оценки параметров которого формируют сигнатуры классов. Так, сигнатура каждого k-го класса включает в себя параметры вектора средних значений Uk и ковариационной матрицы ΣUk признаков.

В основу алгоритма локально-адаптивной классификации положен подход, предполагающий на первом этапе формирование для рассматриваемой территории пространственного распределения сигнатур на основе репрезентативной совокупности эталонных объектов (обучающей выборки) с известной принадлежностью к одному из классов заданного множества. Блок-схема алгоритма приведена на рис. 1.

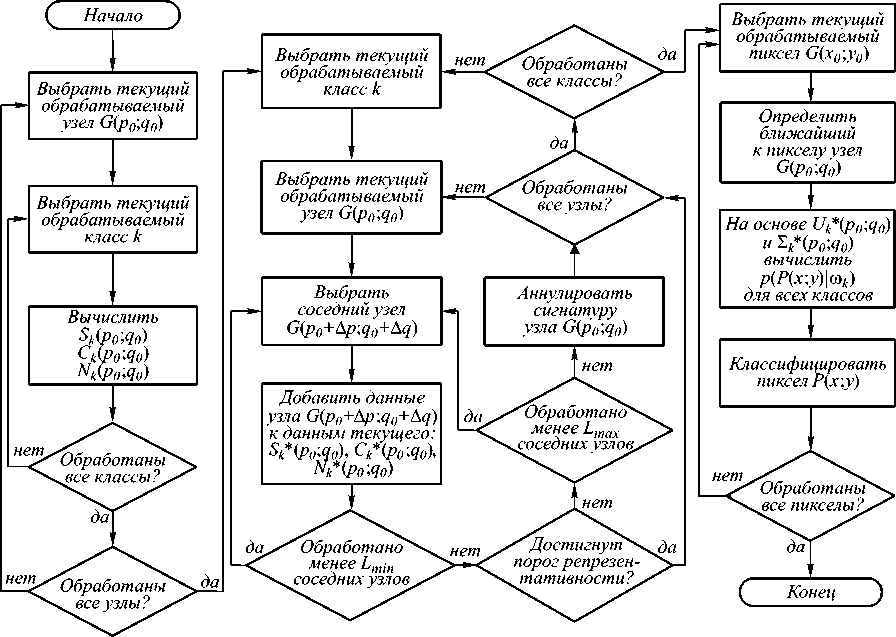
Рис 1. Блок-схема алгоритма локально-адаптивной классификации LAGMA

В качестве источников данных для формирования обучающей выборки часто выступают существующие тематические карты, данные наземных обследований, результаты визуальной интерпретации спутниковых изображений, знания экспертов.

Пространственное распределение локализованных сигнатур описывается их значениями в узлах G ( p, q ) регулярной прямоугольной сети с шагом d , где p и q – порядковые номера узлов по осям x и y соответственно (рис. 2). Обучение классификатора, включающее в себя два описанных ниже логических этапа, направлено на оценку в узлах G ( p, q ) параметров локализованных сигнатур U k ( p, q ) и Σ k ( p, q ) для каждого k -го класса.

Первоначально для каждого узла G ( p, q ) на основе расположенных в границах соответствующей клетки эталонных пикселов вычисляются величины:

S_kⁱ ( p ; q ) – сумма значений i -го признака k -го класса;

Cki,j(p; q) – сумма произведений значений i-го и j-го признаков k-го класса;

N k ( p, q ) – количество эталонных пикселов k -го класса.

Указанные величины используются для оценки элементов Covⁱ_k ^{, j} ( p ; q ) ковариационной матрицы

Σ k ( p, q ) на основе следующего выражения:

Cov , ( p ; q ) = C k^{,j( p} ; q ) — S ⁽ p ; q ) S k⁽ p ^; q ) ^k            N_k ( p ; q ) N_k ( p ; q ) N_k ( p ; q ) ^.

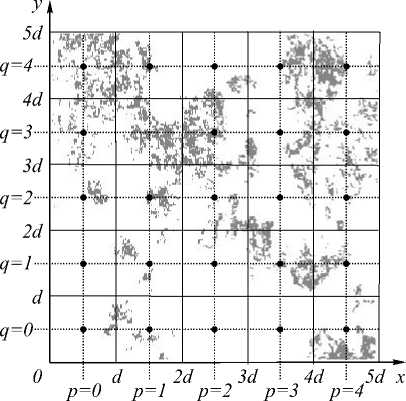
Рис 2. Локализация сигнатур классов в узлах регулярной сети

Оценка элементов Covⁱ_k ^{, j} ( p ; q ) ковариационной матрицы и средних значений признаков на основе S_kⁱ ( p ; q ) и N_k ( p ; q ) позволяет получить параметры сигнатур U k ( p ; q ) и X k ⁽ p ; q ).

Как видно из рис. 2, обучающая выборка эталонных пикселов, как правило, имеет пространственно неравномерное распределение. При этом в случае отсутствия эталонных пикселов k -го класса в окрестности узла G ( p ₀; q ₀) вычисление параметров U_k ( P 0 ; q 0 ) и X _k ( p 0 ; q 0 ) оказывается невозможным. Кроме того, при малых значениях N_k ( p ₀; q ₀) возрастает влияние случайных ошибок в обучающей выборке. Для учёта этого фактора метод предусматривает задание порога репрезентативности T , характеризующего минимально допустимое количество эталонных пикселов для оценки локальных сигнатур классов. Это приводит к появлению узлов, не обеспеченных значениями параметров сигнатур некоторых классов и, как следствие, к необходимости проведения второго этапа обучения классификатора.

На втором этапе для каждого не преодолевшего порог репрезентативности ( N k ( p 0 , q 0 )G(p0, q0) проводится обработка данных соседних клеток. Количество используемых соседних клеток зависит от величины T, числа эталонных пикселов в клетке N_k(pо, qо) и соседних клетках N_k (p0 + Ap; q0 + Aq). Кроме того, методом предусмотрено задание параметров Lmin и Lmax, ограничивающих число используемых соседних клеток снизу и сверху соответственно.

Число используемых соседних клеток итеративно увеличивается, начиная с L min до величины, соответствующей достижению порога репрезентативности T . Если порог T не был преодолён при достижении числа ближайших клеток значения L max , то сигнатура узла G ( p ₀; q ₀) для класса k считается несуществующей.

Расширение анализируемой для оценки параметров локальной сигнатуры класса окрестности осуществляется дискретно путём последовательного включения соседних клеток, находящихся на одинаковом удалении от узла G ( p ₀; q ₀) , и обобщения полученных на первом этапе обучения величин S k ⁽ p о ^+A p ; q о ^+A q ), C k ^, j ⁽ p 0 ^{+ A} p ; q 0 ^{+ A} q ) и N_k ( p 0 + A p ; q ₀ + A q ). При этом новые характеристики узла S_k^{i *} ( p ₀; q ₀), C_k^{i , j *} ( p ₀; q ₀) и N_k ^* ( p ₀; q ₀)вы-числяются как суммы соответствующих величин, полученных для соседних узлов на первом этапе обучения.

По результатам второго этапа обучения, для класса k в узлах, для которых справедливо выражение N_k * ( p ; q ) >  T , определяются с использованием выражения аналогичного (1) параметры сигнатур U_k * ( p ; q ) и X _k * ( p ; q ) для последующей обучаемой классификации.

В основу алгоритма локально-адаптивной классификации могут быть положены различные решающие правила, включая методы максимального правдоподобия, минимального расстояния или параллелепипеда [1]. К настоящему времени в составе разработанного программного комплекса LAGMA реализован алгоритм классификации на основе метода максимального правдоподобия.

В соответствии с решающим правилом максимума правдоподобия, пиксел P ( x ; y ) относится ко множеству го l пикселов класса l в том случае, если для всех k =1, 2…m выполняется условие:

p ^{( го} i ) p ⁽ P ⁽ x ; У ) I ^го i ) >  p ^{( го} k ) p ⁽ P ⁽ x ; У ) I ^го k ), ⁽²⁾ где p ( го l ) и p ( го _k ) - априорные вероятности классов l и k ;

p ( P ( x ; y ) | го l ) и p ( P ( x ; y )| го _k ) - плотности вероятности отнесения пиксела P ( x ; y ) ко множеству пикселов класса l и множеству пикселов класса k .

В свою очередь, плотность вероятности определяется по формуле:

exP [ ^- 2⁽ B ⁽ x ; У ) ^- U_k *⁽ p ; q )) T ^X _k *⁽ p ; q ^)- 1 ⁽ B ⁽ x ; y ) ^- U_k *⁽ p ; q ))

p ⁽ P ⁽ x ; y ) | ^го k ) =----------------------------------------------1--------------------------

(2 n ) 2 |X k *( p , q )| ²

где B ( x ; y ) – вектор признаков пиксела P ( x ; y ) ; n – число признаков.

При классификации используются параметры

Uk*(p; q) и Xk*(p; q) локализованных сигнатур, вы- численных на втором этапе обучения. Для классификации пиксела P(x; y) используются сигнатуры ближайшего узла G(p; q) , порядковые номера которого в строках и столбцах регулярной сетки с шагом d определяются по формулам p = x / d и q = y / d .

Наряду с сигнатурами, характеризующими локализованные значения признаков, при классификации используются априорные вероятности, полученные на основе данных об ареалах распространения различных типов земного покрова в пределах рассматриваемой территории. В решающем правиле (2) априорная вероятность класса используется в качестве коэффициента, определяемого в виде дробной величины в диапазоне от 0 до 1 для каждого класса и каждого пиксела территории. Априорные вероятности могут быть получены в результате обобщения обучающей выборки таким образом, что в окрестности эталонных пикселов заданного класса её значения максимальны и снижаются по эмпирически подобранным правилам по мере удаления.

Данные спектрорадиометра MODIS

Спектрорадиометр MODIS (Moderate Resolution Imaging Spectroradiometer) установлен на борту спутников Terra и Aqua. Ширина полосы захвата прибора составляет 2330 км при угле горизонтальной развёртки ± 55о. Прибор ведёт съёмку в 36 каналах видимого и инфракрасного (ИК) диапазонов длин волн с пространственным разрешением 250 м, 500 м и 1000 м в зависимости от канала.

Данные MODIS распространяются Геологической службой США . Для разработки описанных в настоящей работе методов была сформирована база данных MODIS, в которую вошли стандартные продукты MOD09 за период 2000-2010 годов. Набор данных включает измерения коэффициента спектральной яркости (КСЯ) в красном (620-670 нм) и ближнем ИК (841876 нм) каналах с пространственным разрешением 250 м. MOD09 содержат также измерения КСЯ в каналах голубого (459-479 нм) и среднего ИК (16281652 нм) диапазонов с пространственным разрешением 500 м. В дополнение к измерениям КСЯ, данные MOD09 содержат информацию об угловых характеристиках Солнца и прибора в момент съёмки. Данные MOD09 представлены в синусоидальной картографической проекции и разбиты на гранулы, регулярно покрывающие поверхность Земли.

Предварительная обработка данных MODIS

Предварительная обработка данных MODIS направлена на снижение влияния различных мешающих факторов и, следовательно, повышение эффективности тематической обработки данных. Согласно [8] предварительная обработка данных MODIS предусматривает выполнение следующих последовательных этапов:

• 1)    маскирование пикселов по их значениям угловых характеристик освещения и наблюдения;

• 2)    детектирование пикселов, подверженных влиянию снежного и облачного покровов;

• 3)    детектирование пикселов, соответствующих участкам теней от облаков;

• 4)    статистическая фильтрация временных рядов данных;

• 5)    построение композитных изображений максимально свободных от влияния мешающих факторов.

Для выбора наблюдений, пригодных для дальнейшей обработки по геометрическим условиям освещения и наблюдения, используется совокупность пороговых критериев VZA > 40⁰ и SZA > 80⁰, где VZA – зенитный угол наблюдения, SZA – зенитный угол Солнца.

Детектирование участков с наличием облачного и снежного покровов выполняется с использованием данных измерений КСЯ в голубом R3 (459-479 нм) и среднем ИК R6 (1628-1652 нм) каналах MODIS. В ос- нове данного алгоритма детектирования лежит ис- пользование нормализованного разностного индекса снега NDSI, определяемого по формуле (3):

NDSI =

R 3 - R 6

R 3 + R 6

и априорных знаний об отражательных свойствах поверхности.

Примем на данном этапе, что каждый пиксель относится к одному из четырёх классов: облачность, полупрозрачная облачность, снег, свободная от влияния облачности и снега подстилающая поверхность (чистая поверхность).

Рассмотрим двумерное пространство признаков R3 и NDSI (рис.3), которое разобьём на четыре области следующим образом:

«снег», если R3 > 0,05 и NDSI > 0,1;

«облачность», если R3 > 0,05 и -0,2 <  NDSI < 0,1;

«полупрозрачная облачность», если R3 > 0,05 и - 0,35 <  NDSI < -0,2;

«чистая поверхность» во всех остальных случаях.

Пиксели, окружающие классы «облачности» и «полупрозрачной облачности», также относятся к этим классам, если их значения R3 не меньше значений крайних пикселов, принадлежащих к классу.

Используя предполагаемое значение максимальной высоты облаков, на следующем шаге рассчитывается местоположение соответствующих им теней с использованием данных об углах наблюдения и положения Солнца (рис. 4).

Поскольку точные данные о высоте облаков отсутствуют, в качестве максимально возможной соответствующей величины было выбрано значение h = 12 км, а алгоритм включил в себя построение зоны, заведомо содержащей подлежащие выделению пикселы. Если ввести прямоугольную декартову систему координат с началом в данном соответствующем облаку пикселе с осью Ox, направленной на север, и осью Oy, направленной на восток, тогда радиус-вектор смещения тени на изображении относительно облака высотой H задаётся в этой системе следующими координатами:

x = H ( cos( ψ ) tg( θ ) - cos( β ) tg( δ ) ) y = H ( sin( ψ ) tg( θ ) - sin( β ) tg( δ ) ) ^,

где ψ - азимутальный угол наблюдения, θ - зенитный угол наблюдения, β - азимутальный угол Солнца, δ - зенитный угол Солнца.

NDSI

Снег

Чистая поверхность

0,1-

Облачность

R3

0,05

Чистая поверхность

-0,2-

-0,35—

Полупрозрачная облачность

Чистая поверхность

Рис. 3. Пороговое разделение пикселов «чистой поверхности», облачности и снежного покрова в двумерном пространстве R3-NDSI

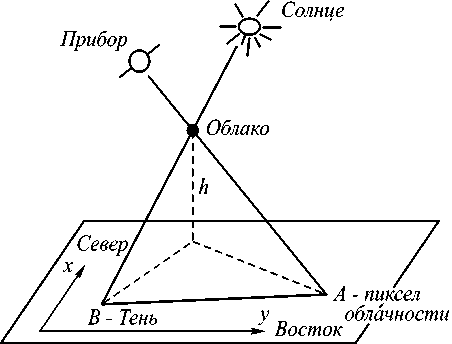
Рис. 4. Геометрическое расположение линии тени от облака на наблюдаемой спутниковым прибором поверхности Земли

Как правило, геометрическая линия тени, описываемая формулой (5), захватывает не только теневые пиксели, но и чистую поверхность, что обуславливает необходимость дополнительного анализа пикселов, отнесённых к классу геометрической тени. Так, при рассмотрении линии тени можно определить реальную границу затенённых участков по скачкообразному росту (рис. 5) отражательной способности R2 в ближнем ИК канале (841-876 нм) MODIS.

Этап статистической фильтрации временных рядов направлен на выявление неверно выделенных теней, возникающих за счёт имеющего место ошибочного отнесения участков снега с недостаточно высоким значением индекса NDSI к классу облачности. Ложной тенью считается пиксел, не попадавший ни разу в класс «чистая поверхность» в течение двадцати дней (десять дней до даты начала интервала и десять дней после) при условии выпол- нения следующего условия для пикселов геометрической тени:

R 1( Θ ^* , t ) > M R 1 ( Θ ^* , t ) +σ R 1 ( Θ ^* , t ), (6) где σ _{R 1}( Θ ^* , t ) – стандартное отклонение от среднего значения M_{R 1} ( Θ ^* , t ) .

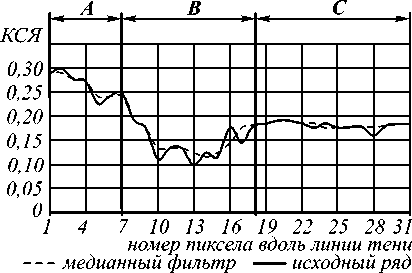
Рис. 5. Профиль значений КСЯ в ближнем ИК канале MODIS по линии тени от облака. Зоны линии тени: А – зона остаточной облачности, Б – область тени, В – область избыточно выделенной тени

Фильтрация остаточного влияния мешающих факторов и детектирование сбойных пикселов осуществляется на основе анализа временных рядов данных MODIS за указанный выше двадцатидневный интервал времени. Отделение «зашумлённых» пикселей происходит по критерию превышения удвоенного стандартного отклонения σ _{R 6} ( Θ ^* , t ) от среднего значения M_{R 6} ( Θ ^* , t ) :

| R 6( Θ ^* , t ) - M R 6 ( Θ ^* , t )| ≥ 2 ⋅σ R 6 ( Θ ^* , t ).           (7)

В результате выполнения перечисленных выше шагов фильтрации данных MODIS формируется набор «масок» с указанием статуса каждого пиксела, используемых для последующего осреднения очищенных данных за заданные интервалы времени.

Предварительная обработка данных MODIS позволяет в значительной мере компенсировать влияние мешающих факторов и даёт возможность построения на основе ежедневных данных композитных изображений за различные промежутки времени с редуцированным влиянием облачного и снежного покровов, теней и аппаратурных шумов. В данной работе используются еженедельные композитные изображения для учёта сезонной динамики спектрально-отражательных характеристик земного покрова. На основе значений КСЯ в каналах композитных изображений проводится расчёт значений спектрального вегетационного индекса (ВИ). При решении задач мониторинга пахотных земель на больших территориях с меняющимися яркостными характеристиками почвенного покрова эффективным является использование почвенно-адаптивных ВИ. Перпендикулярный вегетационный индекс PVI в значительной мере независим от яркости почвенного покрова и тесно коррелирует с объёмом зелёной биомассы и концентрацией хлорофилла в растениях. Это делает возможным использование PVI для мониторинга сельскохозяйственной растительности и пахотных земель больших территорий. Значение PVI рассчитывается в двумерном пространстве значений КСЯ красного и ближнего ИК диапазонов как евклидово расстояние от данной точки до линии почв. С использованием полученного в работе [7] уравнения для линии почв, PVI вычисляется по формуле

PVI ( R 1 ,R 2 ) = - 0,74 R 1 + 0,67 R 2 - 0,034, (8) где R ₁ и R ₂ соответствуют измерениям КСЯ в красном и ближнем ИК каналах. На основе рассчитанных значений PVI формируются временные серии данных с последующим сглаживанием временных рядов на основе скользящих статистических фильтров для снижения влияния случайного шума и заполнения пропусков данных.

Спектрально-динамические признаки и метод распознавания используемых пахотных земель

Некоторые типы земного покрова, к числу которых относятся и используемые пахотные земли (ИПЗ), как правило, невозможно надёжно распознавать на основе одномоментных спутниковых данных или даже регулярных наблюдений в течение одного сезона. Так, опираясь на анализ только лишь сезонной динамики КСЯ, в зависимости от моментов наблюдений и текущего состояния пашни, участки ИПЗ часто можно ошибочно отнести к классу открытых почв или лугов (степей). Наличие многолетних рядов спутниковых наблюдений открывает возможности разработки новых информативных признаков распознавания ИПЗ и других типов земного покрова.

В данной работе используются признаки, построенные на основе многолетних рядов PVI, учитывающие характерные отличия между естественной и сельскохозяйственной растительностью ввиду наличия на участках последней севооборота.

Приведённые в качестве примера на рис. 6 временные ряды PVI получены для двух участков пашни и естественной растительности, находящихся в близких почвенно-климатических условиях. Представленный рисунок показывает, что многолетние ряды PVI рассматриваемых классов имеют характерные особенности, позволяющие разработать признаки распознавания ИПЗ. В частности, из рисунка видно, что культурная растительность начинает своё ежегодное развитие позже естественной (ввиду проведения посевных работ), интенсивнее развивается, достигая более высоких значений PVI, а затем теряет хлорофилл и исчезает (в результате уборки урожая) раньше естественной растительности.

В таблице 1 приведены разработанные признаки распознавания пашни и даётся характеристика особенностей их использования. При этом признаки основной группы (первые три в таблице 1) обеспечивают хорошую локальную разделимость практически в любом регионе России и, следовательно, применимы для всей территории страны. Признаки распознавания вспомогательной группы (последние три в таблице 1) обладают хорошим уровнем разделимости лишь в отдельных регионах для земель с определёнными типами севооборота. Это ограничивает область их применения для картографирования пахотных земель, но позволяет использовать при решении вспомогательных задач, таких как формирование обучающей выборки или фильтрация ошибочно распознанных участков на этапе постклассификационной обработки результатов.

Таблица 2 даёт представление о разделимости участков пашни и других типов земель на основе признаков распознавания основной группы.

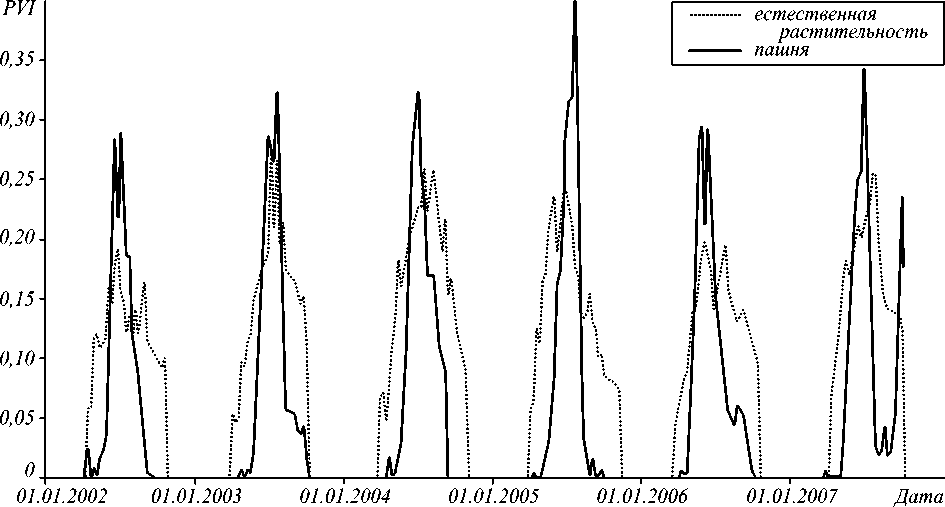
Рис. 6. Примеры многолетних временных рядов PVI с характерными для пашни и естественной растительности межгодовыми и сезонными различиями. L₁ / ₂ иллюстрирует один из признаков распознавания ИПЗ (см. таблицу 1)

Таблица 1. Признаки распознавания используемых пахотных земель на основе многолетних рядов данных MODIS

Название	Формула	Описание	Особенности
			D	K	R	C	V
Индекс кратчайшего сезона вегетации	L 1/2 = min ( t Lj - t F ), j = 1.. N PVI PVI ( t L ) = PVI (t F ) = -mx- , t L >  t max , t F <  t max	Минимальный для ряда лет отрезок времени, когда в течение года значения PVI превышали половину его сезонного максимума.	+	–	–	+	–
Индекс весеннего развития растительности	MSI = min У PVL j = 1.. N              i i e spw	Многолетний минимум интеграла PVI в период 1 января - 15 июня каждого года наблюдений.	–	+	+	+	–
Индекс сезонного снижения фитомассы	^^pVI min e sw NSMI = const - j = N-------- Ц PVI j = 1 i e sw	Нормированная сумма многолетних сезонных минимумов PVI в период 15 мая - 15 сентября каждого года наблюдений.	+	+	+	–	+
Индекс межгодовых различий динамики растительности	K = = min (Cor ( PVI(Year ), PVI(Year ))) i, j e l.. N                               ‘                        j	Минимум всех возможных значений межгодовых корреляций временных рядов PVI.	+	+	+	–	–
Индекс межгодовой изменчивости фитомассы	D = SD (V pvi ) i = 1N ^      j	Стандартное отклонение сумм накопленных за различные годы значений PVI.	–	+	+	–	–
Разностный индекс сезонного пика вегетации	T = Med ( PVI Year j - Pi! ' '' ) max         mean j = 1.. N	Многолетняя медиана разности максимального и среднего значения PVI.	+	+	+	+	–