Распознавание симметрии полутоновых изображений с помощью интегрального преобразования
Автор: Мнухин Валерий Борисович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 2 т.11, 2013 года.
Бесплатный доступ
Предлагается метод распознавания групп симметрий полутоновых изображений, основанный на использовании специального интегрального преобразования.
Обработка изображений, распознавание симметрии, интегральное преобразование, преобразование фурье-меллина, частотная область
Короткий адрес: https://sciup.org/140191622
IDR: 140191622 | УДК: 528.854
Текст научной статьи Распознавание симметрии полутоновых изображений с помощью интегрального преобразования
Изучение симметрии изображений является в настоящее время одним из активно развиваемых направлений теоретической информатики. Работы в этой области активно стимулируются, в частности, тем, что группы симметрий изображений не зависят от их размеров, поворотов, яркости, плотности и центрирования, являясь тем самым сильными дескрипторами изображенных объектов [1-3].
В настоящей работе рассматривается задача распознавания группы симметрий изображения с точностью до изоморфизма. Для ее решения предлагается новое двумерное интегральное преобразование, являющееся непрерывным по первой переменной и дискретным по второй. Идея его построения основана [3] на рассмотрении Фурье-образа изображения в полярной системе координат, что позволяет трансформировать вращения в сдвиги и находить инварианты изображения относительно преобразований симметрии.
Отметим, что вводимое преобразование до некоторой степени аналогично так называемому преобразованию Фурье-Меллина [4], инвариантному относительно как сдвигов и вращений, так и масштабирования. Заметим, что последнее важно для эффективного решения задач совмещения изображений [5], однако избыточно при распознавании симметрии, а использование преобразованием Фурье-Меллина полярнологарифмической системы координат приводит к значительным вычислительным сложностям. В частности, основанный на нем метод [6] распоз- навания симметрии требует априорного знания координат центра симметрии.
Предлагаемый в работе подход свободен от указанных недостатков. Простота аналитического выражения рассматриваемого преобразования позволяет в непрерывном случае сформулировать его свойства в окончательной форме. На их основе устанавливается ряд следствий, позволяющих эффективно распознавать группу симметрий. Работа выполнена при поддержке РФФИ, проекты № 11-07-00591 и №13-07-00327.
Группа симметрий изображения
Будем считать, что на действительной плоскости R2 введена декартова система координат хОу . Под изображением (точнее, под плоским непрерывным полутоновым финитным изображением) будем понимать неотрицательную действительную ограниченную функцию /U, у), определенную всюду на R2 , но отличную от нуля только внутри некоторой области I с R конечного диаметра. Чтобы ввести понятие группы симметрий, рассмотрим следующие элементарные преобразования изображений:
-
1) сдвиг Т на вектор й (жо ’ У о)■
W = Кх - х01у - у0);
-
2) вращение R на угол а вокруг начала координат O :
R [/] = /(ж cos а — у sin q, х sin а + у cos а-);
-
3) отражение M относительно оси :
M\f \ = f^. ~У) •
Рассматривая их композиции, получаем более сложные преобразования. В частности, нам понадобится преобразование ML отражения относительно прямой L проходящей через точку а = ^0,У0) и наклоненной к оси Ох на угол а. Как нетрудно показать,
Mr = TR, МТ .
L а, 2а —а
Определение 1. Будем говорить, что изображение f обладает отражательной симметрией относительно прямой L (или симметрично относительно L ), если МДЫ = M для всех (x,y) G R2. При этом L называется осью симметрии.
Чтобы ввести понятие вращательной симметрии, рассмотрим преобразование R вращения на угол a вокруг точки a :
R =TRT .
a,a a ', —a
Определение 2. Будем говорить, что изображение / обладает вращательной симметрией бесконечного порядка в точке d, если R„,W\ = / для всех Cl . Если же найдется угол 0, (0 3 < 2тг), такой, что W = f> но RJJ] - / для всех меньших углов Cl, 0 < ci < /3, то в точке a изображение имеет вращательную симметрию порядка к = 2тг / 0, где, как нетрудно заметить, число к > 1 является целым. Точка ci называется центром вращательной симметрии.
Всевозможные композиции элементарных преобразований сдвигов ^a ’ вращений R и отражения M образуют бесконечную группу перемещений Г, являющуюся подгруппой группы всех аффинных преобразований плоскости [7]. Таким образом, Г естественно действует на множестве изображений.
Определение 3. Группой симметрий изображения / называется его стабилизатор Г(/) в группе перемещений. Другими словами, это множество всех тех перемещений плоскости, которые не изменяют данное изображение.
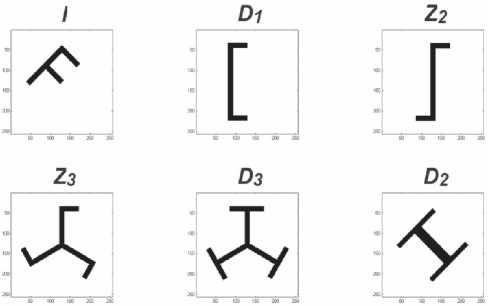
Рис. 1. Примеры изображений с небольшими группами симметрий
Классы изоморфизма групп симметрий финитных изображений хорошо известны [7]. Это либо
-
а) конечные циклические группы Z порядка к > 1, порождаемые вращением вокруг точки a на угол 2тг / к , (случай к = 1 соответствует отсутствию нетривиальных симметрий), либо
-
б) конечные диэдральные группы Dk порядка 2к>2, порождаемые отражением относительно некоторой прямой и вращением порядка к с центром на даннной прямой, либо
-
в) бесконечная ортогональная группа 0(2), являющейся группой симметрий окружности.
Заметим, что обычно считается, что диэдраль-ная группа D имеет порядок 2к > 4. Нам будет удобно рассматривать также группу D^ порядка 2, порождаемую единственным отражением, отличая ее от группы Z порождаемой вращением на 180°. Несмотря на изоморфизм D^Z2, соответствующие этим группам симметрии различны (см. рис. 1). В данной работе рассматривается проблема распознавания симметрии плоского финитного изображения, заключающаяся в нахождении его группы симметрий с точностью до изоморфизма.
Распознавание симметрии непрерывных изображений
Введем интегральное преобразование, играющее ключевую роль в нашем подходе к проблеме распознавания симметрии. Оно основано на двумерном преобразовании Фурье, определяемом [8] следующим образом:
F[f] = F('lk ^ =
= J J /(ж,7/)ехр{-2тгг(
xu + yv)}dxdy,
где сходимость немедленно вытекает из наложенных на функцию f^i dk ограничений. Фурье-образ F^, v) определен на плоскости uOv, называемой частотной областью. Введем в ней полярную систему координат rOip с тем же самым началом O и с полярной осью y? = 0 , совпадающей с положительной полуосью Ox . Рассмотрим Фурье-образ F(u, v) в этой системе, полагая
Ф(т,<р) = F(r
cos
sin ?).
Наложим на функцию / еще одно ограничение. Поскольку реальные изображения являются гладкими, условимся считать
f^-> y)
бесконечно дифференцируемой в каждой точке по любому направлению. Тогда для всякого фиксированного полярного угла ^o e [0,
tf]
модуль функции
Ф^о) быстро убывает с ростом радиуса г, что гарантирует корректность определения следующего преобразования: НШ = н^ Л =
= J*
^(t*,^)!
ехр{—z(wr + 2n?)}drd(p.
О о где непрерывная переменная W принимает всевозможные действительные значения, а дискретная переменная 77 пробегает множество всех целых чисел Z. Таким образом, Я(ш, п) можно считать комбинацией некоторого одномерного преобразования Фурье (по переменной w)и коэффициентов ряда Фурье (по переменной п Y Функцию H^w, 77) условимся называть H-образом изображения у при его H-преобразовании н\Л • Ее можно рассматривать как бесконечную (в обе стороны) последовательность функций
H[f]
: ...,Я(^-1),Я(«',0),Я(^Д),...
Рассмотрим свойства преобразования Я[/]. Прежде всего отметим, что посколькуонозависит только от энергетического спектра изображения,
H
-преобразование не является ни обратимым, ни линейным. Покажем, как меняется
H
-образ изображения при его сдвигах и вращениях.
Утверждение 1. Преобразование Я[/] инвариантно относительно сдвигов. При вращении изображения у на угол а вокруг произвольной точки его
H
-образ умножается на фазовый множитель :
H\RJ\ = e^H^nY
Тем самым модуль
H
-образа изображения инвариантен как относительно сдвигов, так и относительно вращений.
Рассмотрим отражения
^L
изображения относительно некоторой прямой .
Утверждение 2. Если прямая
L
образует с осью
Ох
угол а, а
H
-образ исходного изображения / равен Я(Ш,77.) = Я[/], то
H\MJ\
= е4!№Я(«7,-77).
Таким образом, получаем следующий тест на отражательную симметрию изображения.
Следствие 1. Если изображение / симметрично относительно некоторой прямой, образующей с осью
Ox
угол
α
, то для
H
-образа этого изображения выполняется тождество
Н^п)
= е4"юЯ(™,-77).
В частности, если для некоторых значений переменных ТУ И 77 справедливо неравенство |Я(ш, 77)| ^ |Я(ш, — 77)|, то изображение не обладает отражательной симметрией. Аналогичный результат о вращательной симметрии изображения имеет следующий вид.
Утверждение 3. Если изображение / имеет бесконечную группу симметрий 0(2), то
H(w,
7?,) = О для всех 77 ^ О . Если же группа симметрий Г(/) конечна и содержит вращение порядка
к,
то
Н(ш, 77) = 0 для всех 77 ^ О mod h(k), где h(k) =
Л к
/2,
если к нечетно, если к четно. Другими словами, периодическое появление в последовательности Я[/] нулевых функций указывает на вращательную симметрию изображения, причем «ширина нулевого интервала» связана с порядком симметрии.
Рис. 2. Вид
H
-преобразования изображения c вращательной симметрией
Из предыдущих результатов вытекает тест на диэдральность группы симметрий изображения. Следствие 2. Если изображение / имеет диэд-ральную группу симметрий порядка 2^, то H(w, п) = - е^Н^-п), О,
?7. = 0mod/7(A;),
иначе
где а является углом наклона произвольной оси отражения данного изображения к
Ох
. Корректность данного утверждения следует из того, что разность углов наклона двух различных осей отражения всегда кратна 7Г /
к.)
Распознавание симметрии цифровых изображений ||(№ F-F3? W|—---->0, \ Л О / J \'X Реализация предложенного метода распознавания симметрии для практически значимого случая цифровых изображений имеет ряд особенностей. Обсудим их подробнее, предполагая для простоты изложения, что размер изображения нечетен. Для фиксированного положительного нечетного целого N = 2M + 1 > 3 рассмотрим в дискретной плоскости Z* квадрат S = [-M, M\ x \-M, M] C z2. Произвольную неотрицательную ограниченную функцию M^^^R дискретных аргументов X и у назовем цифровым изображением размера NxN. Под его диаметром будем понимать наименьшее целое d = 26 + 1 > 0 такое, что /(ж,?/) = 0 всюду вне некоторого квадрата max о
Рассмотрим в области
S
двумерное дискретное преобразование Фурье (ДПФ):
что позволяет использовать результаты предыдущего раздела в дискретном сучае при выполнении условий
N
> 0 и
d < N.
Кроме того, в то время как в непрерывном случае началом полярной системы координат в частотной области может быть только (0,0),в дискретном случае в этом качестве можно использовать также точ-ку,«диаметрально противоположную» (0, 0)на торе
T
. Соответственно возникают два варианта дискретного
H
-преобразования, которые естественно назвать низкочастотным F[/] и высокочастотным F[/]. Свойства этих преобразований дополняют друг друга, и их можно использовать для распознавания симметрии совместно. Для построения F[f] рассмотрим в частотной области
T
«полукруг»
C = |(u,v) E T : и + v2 < M2, и > o| и определим отображение P-.T ^C как P^r,^) = (zi,v), где r^ E [—M, M], U.yles 2тп , , exp - — (их + vy) - ■ n = r + M ----sin
ТПуО
N
Его частотная область
и Ou
представляет собой дискретный тор
T
, получающийся из квадрата
S
отождествлением противолежащих сторон. Заметим, что частотную область непрерывного преобразования Фурье можно считать сферой (после добавления бесконечно удаленной точки). Различная топология этих областей приводит к отличиям в свойствах непрерывного и дискретного преобразований Фурье. В частност
и,
доказательства утверждений предыдущего раздела существенно опираются на то, что непрерывное преобразование Фурье коммутирует с вращениями,
FR = RF
. Для цифровых изображений даже корректное определение вращения явлется нетривиальной задачей, допускающей различные решения. Обычно вращение вводится как
3?o[/] = /([^]mod7V, [y]mod7V), где
X = x
cos
a — у
sin
a, Y = x
sin
a + у
cos
a,
а № и [У] означают ближайшие целые к
X
и
Y
соответственно. Условимся называть № дискретным вращением. Как нетрудно заметить, ДПФ уже не коммутирует с № . Вместе с тем можно показать, что для цифровых изображений фиксированного диаметра
d
< oo имеет место сходимость
Для ДПФ
FVA = F(u,v)
построим
Ф(г, у?) = FI P(r, у?) I, где (г, у?) E T, и определим низкочастотное H-преобразование следующим образом:
ШЛ
= Я(ш,п) =
=p- E 1ф<г'И i.r.^eT 2tv% , .
exp ■ ——
+ ipn) .
Смеща
я
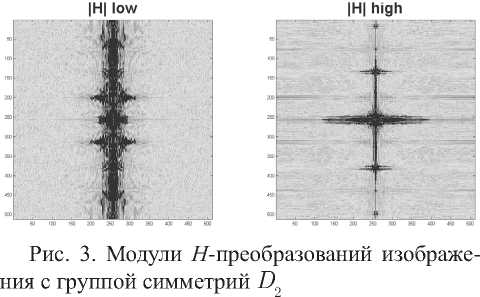
начало координат,аналогично можем определить F[/]. На рис.3 показана визуализация модулей
H
-преобразований последнего из изображений рис.1.Их характерная симметричность указывает на отражательную симметрию исходного изображения.
Заметим, что наиболее естественное определение функции ф с помощью отображения
P
не свободно от недостатков.Действительно,
P
не является,вооб-ще говоря,ни инъективным,ни сюръективным,что связано с принципиальной невозможностью вполне адекватного определения полярной системы координат на дискретной плоскости [9].На практике лучшие результаты дает использование функции
Ф^у ^ = аФ(г, у?) + (1 - а)Ф(г, у?), где О < а < 1,аФ определяется следующим образом: рассмотрим отображение Q-.C^T такое, что <Ж^ = (г, у?), где у? = ^7V arg(,z) / тгj, т = [2 | z |], z = и + ги, причем arg(^) е [—тг / 2, тг / 2]. (В некотором смысле Q подобно обратному к р ) Теперь если (г, ^ = Q(u, v) для (и, v) G С , то положим Ф^r,y?) = F(u, v); в противном случае Ф(?',у?) = О. Выбор значения коэффициента а зависит от специфики решаемой задачи; в данной работе полагалось а = 0,5.
Рассматривая применимость результатов предыдущего раздела к цифровым изображениям, следует учитывать, что даже абсолютно симметричный относительно некоторой оси отражательной симметрии объект может потерять эту симметричность при поворотах изображения. Поэтому анализ
H
-преобразований, превращающихся для цифровых изображений в
(N
х 7V) -матрицы, следует проводить статистическими методами.
Несмотря на то что приведенные выше результаты дают только необходимые условия наличия симметрий изображений, они позволили корректно распознать группы симметрий в сделанных тестовых примерах. Выводы Предложен метод распознавания групп симметрии плоских финитных изображений, осно- ванный на рассмотрении симметрий в частотной области. Вводится интегральное преобразование, позволяющее получить эффективно вычислимые инварианты изображений.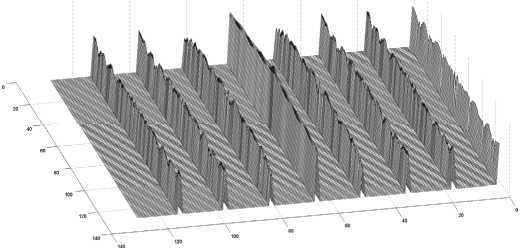

Список литературы Распознавание симметрии полутоновых изображений с помощью интегрального преобразования
- Каркищенко А.Н., Мнухин В.Б. Классификация изображений периодических структур на основе непрерывного преобразования симметрии//Интеллектуализация обработки информации (ИОИ-2010). М.: МАКС Пресс, 2010. -С. 359-362.
- Каркищенко А.Н., Мнухин В.Б. Преобразование симметрии периодических структур в частотной области//Математические методы распознавания образов (ММРО-15). М.: МАКС Пресс, 2011. -С. 386-389.
- Каркищенко А.Н., Мнухин В.Б. Распознавание симметрии изображений в частотной области//Интеллектуализация обработки информации (И0И-2012). М.: Торус Пресс, 2012. -С. 426-429.
- Reddy S., Chatterji B. A FFT-based technique for translation, rotation, and scale invariant image registration//IEEE Trans, on Image Processing, Vol.5, 1996. -P. 1266-1271.
- Derrode S., Ghorbel F. Robust and efficient Fourier-Mellin transform approximations for gray-level image reconstruction and complete invariant description//Computer Vision and Image Understanding, Vol. 83(1), 2001. -P. 57-78.
- Derrode S., Ghorbel F. Shape analysis and symmetry detection in gray-level objects using the analytical Fourier-Mellin representation//Signal Processing., Vol. 84(1), 2004. -P. 25-39.
- Никулин В.В., Шафаревич И.Р. Геометрии и группы. М.: Наука, 1983. -239 с.
- Poularikas A.D. The Transform and Applications Handbook. CRC Press, 2010. -1336 p.
- Beylkin G. On the fast Fourier transform of functions with singularities//Appl. Comput. Harmon. Anal., Vol. 2, 1995. -P. 363-381.


