Распознавание типов аберраций волнового фронта, соответствующих отдельным функциям Цернике, по картине функции рассеяния точки в фокальной плоскости с применением нейронных сетей

Распознавание и компенсация аберраций волнового фронта востребованы в различных приложениях, связанных с применением оптических систем от исследования космоса до улучшения зрения [1–9].

Не имея возможности прямым способом измерять фазу светового поля, приходится определять её косвенно, в том числе по измерениям интенсивности светового поля. Существуют различные подходы к решению этой задачи, однако разрабатываются и новые методы.

Одним из известных методов, обеспечивающих высокую точность определения отклонений волнового фронта на весьма значительных размерах апертур, является интерферометрия [10, 11]. Точность интерферометров, особенно гетеродинных, порядка λ / 100. Однако метод имеет и существенные недостатки: трудоёмкость расшифровки интерферограмм, чувствительность измерительной аппаратуры к вибрациям, а также необходимость физического наличия эталонного волнового фронта. На начальных этапах раз-

вития оптического производства для контроля сферических поверхностей использовался теневой метод [12], однако теневые картины с трудом поддаются количественной интерпретации, а теневая установка так же, как и интерферометр, должна обладать высокой жёсткостью и защищаться от вибраций.

Метод Хартмана [13], появившийся несколько позже, отличается тем, что отклонения волнового фронта вычисляются по набору субапертур, покрывающих подлежащую исследованию область. Отклонения волнового фронта вычисляются на основе данных о трассировке лучей, прошедших через субапертуры. Дальнейшим развитием метода Хартмана явился датчик волнового фронта Шака–Хартмана [14–16]. В этом варианте датчика перенос данных об отклонениях волнового фронта в плоскость фотодетектора осуществляется путём установки линзового растра. Каждая из линз образует субапертуру, для которой усреднённо вычисляется соответствующее ей отклонение волнового фронта. Информация о фазе волнового фронта в пределах субапертуры содержится в координатах сфокусированного светового пятна. Ос- новным преимуществом как метода Хартмана, так и датчика волнового фронта Шака–Хартмана является отсутствие необходимости использования эталонного волнового фронта. Недостатки – это чувствительность к вибрациям и изначально дискретный характер измерений. При этом неизбежно теряются данные о части поверхности волнового фронта. Для большинства производимых сейчас датчиков Шака–Хартмана количество субапертур составляет порядка 1000, что не удовлетворяет требованиям многих задач.

Для получения визуальной информации о волновом фронте напрямую, без использования косвенных измерений, можно воспользоваться методом фазового контраста с применением фильтра Цернике [17]. Основной принцип заключается в преобразовании пространственного спектра светового пучка с использованием линзы и фильтра. Введённый фазовый сдвиг создаёт распределение интенсивности в соответствии с информацией о фазе, переносимой более высокими пространственными частотами. Данный метод был успешно применён для анализа аберраций и улучшения разрешения в телескопах, при дешифровке фазово-кодированной информации, а также в микроскопии биологических тканей [18–20]. Нужно отметить, что данный подход требует оптической системы из двух линз (оптический коррелятор) и пространственного фильтра определённого размера. Чтобы динамически подстраивать фильтр для различных исследуемых объектов, необходимо использовать пространственный модулятор света [21], что, однако, дополнительно усложняет и удорожает оптическую систему.

Одним из инструментов описания волновых фронтов, помимо карты отклонений, являются разложения по различным базисам. Наиболее известные базисы разложения – это полиномы Цернике, а также аберрации Зайделя. Заметим, что общепринятым представлением аберраций волнового фронта, в том числе в индивидуальной оптической системе человеческого глаза, являются функции Цернике [22–25]. Аберрационные представления являются более экономными с точки зрения объёмов данных, а также позволяют выделять особенности волновых фронтов, важные для решения конкретных задач. Непосредственное измерение аберрационных коэффициентов возможно лишь для некоторых видов аберраций. В программах обработки данных, поставляемых с датчиками Шака–Гартмана, а также c офтальмологическими аберрометрами, предусмотрено вычисление аберрационных коэффициентов Цернике [7, 8, 26, 27] на основе двумерного массива измеренных значений отклонений волнового фронта в каждой из субапертур. При этом в связи с достаточно грубой дискретизацией данных о волновом фронте вычисление аберраций высоких порядков представляет трудности.

Для прямого измерения коэффициентов разложения волнового фронта используются многопорядковые дифракционные оптические элементы (ДОЭ), со- гласованные с набором функций Цернике [28–30], которые были успешно применены для анализа волнового фронта с небольшими аберрациями [31]. Датчики, основанные на многопорядковых ДОЭ, обеспечивают чувствительность к отклонениям волнового фронта не хуже λ /20, устойчивы к вибрациям и не требуют применения эталонных оптических элементов. Однако этот подход также имеет свои недостатки. Как правило, обеспечивается прямое измерение только модулей коэффициентов разложения, а для полного восстановления волнового фронта необходимо также измерение относительных фаз коэффициентов. В этом случае необходимо существенное усложнение многопорядкового ДОЭ за счёт дополнительных дифракционных порядков, согласованных с суперпозициями базисных функций [32], и потребуется последующая цифровая обработка.

Другая особенность разложения волнового фронта по базису Цернике состоит в ограничении на уровень аберрации. А именно, представление волнового фронта в виде линейной суперпозиции базисных функций возможно только при небольших аберрациях. При увеличении уровня (силы) аберрации зависимость становится нелинейной, и при детектировании обнаруживается вклад «посторонних» порядков [31].

От этого недостатка свободны методы, ориентированные на анализ картины распределения интенсивности, формируемой аберрированной оптической системой в одной или нескольких плоскостях. Например, по картине ФРТ в фокальной плоскости или вне фокуса. Для этого применяются итерационные [33–37] и оптимизационные [9, 38] алгоритмы, а также нейронные сети [39–43]. Нужно отметить, что в этих работах в основном рассматривались слабые аберрации.

Цель данной работы – исследовать возможность применения нейронных сетей для решения задачи распознавания не только типа, но и уровня (величины) аберрации волнового фронта по картине ФРТ в фокальной плоскости.

Таким образом, в данной работе мы используем нейронную сеть для решения задачи регрессии [44]. В задаче регрессии мы стремимся предсказать результат непрерывного значения, такого как вероятность или цена. Эта проблема отличается от задачи классификации, где мы стремимся выбрать дискретную величину из списка классов. Нами использовалась свёрточная нейронная сеть на основе модифицированной архитектуры нейронной сети Xception [45].

1.    Теоретические основы

Рассмотрим аберрированный волновой фронт в виде поля, описываемого следующим образом:

g ( r , Ф ) = exp [ i v ( r , Ф ) ] . (1)

Будем считать, что фаза в (1) представима суперпозицией функций Цернике:

V ( r , Ф ) = £ b nm Z m ( r , Ф ), n , m

где Z m ( r , ф ) - функции Цернике порядка ( n, m ): cos ( m ф )

z m ( r , ф ) = ar ( r ) j I , (3) [ sin ( m ф )

A n = V ^{( n} + 1) / п - нормировочный коэффициент, R_n^m ( r ) – радиальные полиномы Цернике [17] и b nm – коэффициенты суперпозиции.

В когерентном случае ФРТ в фокальной плоскости линзы с аберрированным волновым фронтом (1) можно рассчитать с помощью преобразования Фурье:

G (p, 0) =- x Xf да 2п xj J g (r, Ф)ехр

— i — r P cos( 0-ф ) ^K f

r d r d ф ,

где X - длина волны излучения, f - фокусное расстояние линзы.

Рассмотрим волновой фронт (1), описываемой одной функцией Цернике (2):

g nm ( r , Ф ) = exp [ ib nm Z m ( r , ф ) ] , (5) где величина коэффициента b nm определяет уровень (величину) аберрации.

В табл. 1 показан вид волнового фронта (фаза) и соответствующее распределение амплитуды ФРТ в когерентном случае для различных функций Цернике при b nm = 1.

На рис. 1 показаны аналогичные картины ФРТ для одной и той же аберрации, но с различным значением коэффициента b nm .

Увеличение коэффициента b nm в (5), что соответствует усилению аберрации, приводит к существенным проблемам при использовании датчиков Шака– Хартмана и разложении по базису функций Цернике. В первом случае происходит искажение информации из-за смещения световых пятен в области, соответствующие другим субапертурам. А во втором подходе искажение возникает из-за того, что зависимость коэффициентов разложения становится нелинейной.

Табл. 1. Соответствие картин ФРТ функциям Цернике индексами (n,m)

N ; ( n , m )	Вид волнового фронта (фаза)	Картина ФРТ (амплитуда, негатив)	N ; ( n , m )	Вид волнового фронта (фаза)	Картина ФРТ (амплитуда, негатив)	N ; ( n , m )	Вид волнового фронта (фаза)	Картина ФРТ (амплитуда, негатив)
1 (0, 0)			6 (2, 2)	в	N^	11 (4, -4)
2 (1, -1)			7 (3, -3)		*	12 (4, -2)	W
3 (1, 1)	<111		8 (3, -1)	^^^^^		13 (4, 0)	^B
4 (2, -2)		л	9 (3, 1)	о		14 (4, 2)	®	ig
5 (2, 0)	^^^^^^^	©	10 (3, 3)	6?	*	15 (4, 4)

Как видно из рис. 1, усиление аберрации в рассматриваемом подходе приводит лишь к масштабному изменению картины ФРТ.

В данной работе решалась задача распознавания не только типа отдельной аберрации из 15 вариантов (см. табл. 1), но и уровня аберрации волнового фронта (т.е. величины коэффициента b nm ) по картине ФРТ в фокальной плоскости.

2.    Выбор архитектуры нейронной сети

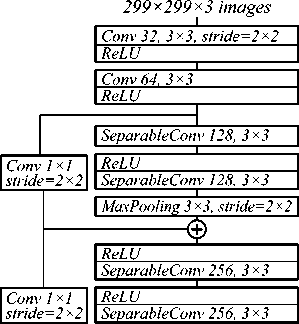
Для решения задачи распознавания аберраций было принято решение использовать готовую архитектуру Xception, представленную в 2015 году [45]. Отличительной особенностью этой модели является использо- вание Depthwise separable convolution. Суть данного приема заключается в разбиении преобразований над входным тензором на каждом слое на два этапа:

• 1)    на первом этапе тензор сворачивается с ядром размерности 1×1. Данная операция носит название “pointwise convolution”;

• 2)    на втором этапе производится стандартная свёртка. После этого результаты свёртки тензора, полученного в результате применения к входному тензору операции “pointwise convolution”, со всеми фильтрами слоя суммируются и формируют выходной тензор слоя. Эта операция носит название “depthwise convolution”.

  а)

  
  
  
  
  
  
  
  
  
  
  
  

Рис. 1. Картины ФРТ для аберрации (n,m)=(2,–2) с различным значением коэффициента:

(а) b 2,–2 = 0,5, (б) b 2,–2 = 0,75, (в) b 2,–2 = 1,5, (г) b 2,–2 = 2

Данный приём позволяет существенно сократить количество весов в нейронной сети, что значительно сказывается на скорости обучения, необходимых для обучения ресурсах и весе предобученной модели. Таким образом, архитектура Xception представляет со- бой оптимальный вариант, обеспечивая достаточную точность обучения, при этом требуя существенно меньше ресурсов.

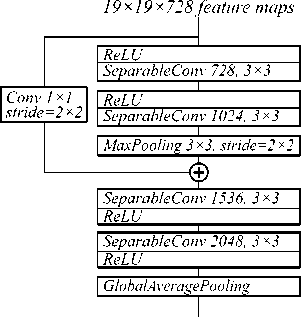
Общий вид архитектуры Xception представлен на рис. 2.

Middle flow

Entry flow

MaxPooling 3x3, stride=2 x.2

19xl9 x 728feature maps

ReLU _____________

SeparableConv 728. 3 x3 I

ReLU _____________

SeparableConv 728, 3 x3 I

ReLU

SeparableConv 728, 3 x3

19xl9 x 728feature maps

Repeated 8 times

Exit flow

2048-dimensional vectors

Optimal fully-connected layer(s)

Conv lx] stride=2 x2

ReLU _______________

SeparableConv 728, 3 x3

ReLU _______________

SeparableConv 728, 3 x3

MaxPooling 3 x3, stride=2x2

Logistic regression

19x19 x 728feature maps

Рис. 2. Полная архитектура Xception

Заметим, поскольку поставленная задача является задачей регрессии, а архитектура Xception разработана для решения задачи классификации, её пришлось подвергнуть небольшим изменениям. В сути своей эти изменения сводятся к добавлению одного полносвязанного слоя для получения размерности выход- ного тензора, равной количеству функций Цернике, рассматриваемых в данной работе (было выбрано равным 15). Для получения значения предсказанных коэффициентов было решено использовать линейную функцию активации, а также дополнить архитектуру dropout-слоем перед выходным полносвязанным слоем для улучшения качества работы.

3.    Описание программной реализации

Для обучения нейронной сети было решено воспользоваться сервисом Google Colab, так как это бесплатный облачный сервис, предоставляющий широкие возможности для использования. Google Colab предоставляет Nvidia Tesla K80 c 12 гигабайтами встроенной видеопамяти DDR5 и 12 гигабайт оперативной памяти. В качестве библиотеки для машинного обучения использовалась библиотека Keras, которая представляет собой надстройку над библиотеками Deep learning4j, TensorFlow и Theano. Её достоинством можно назвать большое количество доступных для использования архитектур и предобученных моделей, высокий уровень абстракции относительно других библиотек, а также большой набор готовых инструментов для обучения и настройки необходимого окружения.

На вход нейронной сети подавались одноканальные изображения размером 299×299 пикселей, примеры которых представлены в табл. 1 и на рис. 1.

4.    Проведение процесса обучения и анализ результатов

Для процесса обучения был выбран оптимизатор Adam, коэффициент обучения для которого был выбран экспериментально и составил 10 ^{- 4}. В качестве функции потерь была выбрана средняя абсолютная ошибка. Процесс обучения вёлся поэтапно, чтобы иметь возможность прекратить его в момент, когда начинает наблюдаться эффект переобучения.

Во время тестовых процессов обучения использовался датасет с 5 тысячами изображений ФРТ, который разделялся в соотношении 4 : 1 на обучающую и валидационную выборки. После датасет был расширен до 15 тысяч изображений. На датасете такого объёма количество эпох, на которых процесс обучения продолжает сходиться, составило 13. Достигнутые показатели ошибок для каждой из аберраций (MSE) и средней ошибки предсказания для всех аберраций определённого типа (MAE) приведены в табл. 2.

Как видно из приведённых в табл. 2 результатов, распознавание происходит достаточно уверенно, причём наблюдается тенденция уменьшения ошибки с увеличением индексов функций Цернике. Такое поведение можно объяснить уширением ФРТ с ростом индексов аберраций (см. табл. 1).

Нужно отметить, что при слабых аберрациях (малых значениях коэффициента) анализ отклонений волнового фронта по картине ФРТ становится за- труднительным, поскольку при слабых аберрациях картины ФРТ слабо отличаются друг от друга и фактически представляют собой яркое фокальное пятно, свойственное идеальному волновому фронту (см. первую строку табл. 1). Эта проблема достаточно известна, и в этом случае имеет смысл использовать другой подход, например, оптическое разложение по базису функций Цернике [30–32]. В методах, основанных на анализе картин ФРТ, чтобы избежать указанных проблем, рассматривают внефокальные плоскости, где картины ФРТ уширенные и размытые [38, 43].

Табл. 2. Соответствие функций Цернике ошибкам предсказаний

N : ( n,m )	MAE	MSE
1: (0,0)	0,033	0,021
2: (1, –1)	0,011	0,004
3: (1,1)	0,014	0,004
4: (2, –2)	0,010	0,003
5: (2,0)	0,013	0,004
6: (2,2)	0,015	0,006
7: (3, –3)	0,013	0,004
8: (3, –1)	0,011	0,004
9: (3,1)	0,011	0,004
10: (3,3)	0,013	0,005
11: (4, –4)	0,011	0,004
12: (4, –2)	0,011	0,003
13: (4,0)	0,010	0,004
14: (4,2)	0,010	0,004
15: (4,4)	0,009	0,003

В данной работе было принято решение в качестве эксперимента провести обучение на датасете из ФРТ, размытом с помощью фильтра Гаусса для увеличения информативной части изображения. Результаты для датасета, состоящего из размытых изображений, представлены в табл. 3.

Табл. 3. Соответствие функций Цернике ошибкам предсказаний на размытом датасете

N : ( n, m )	MAE	MSE
1: (0, 0)	0,040	0,021
2: (1, –1)	0,016	0,006
3: (1, 1)	0,016	0,005
4: (2, –2)	0,013	0,004
5: (2, 0)	0,015	0,004
6: (2, 2)	0,017	0,005
7: (3, –3)	0,013	0,004
8: (3, –1)	0,012	0,004
9: (3, 1)	0,013	0,004
10: (3, 3)	0,014	0,005
11: (4, –4)	0,014	0,005
12: (4, –2)	0,012	0,004
13: (4, 0)	0,015	0,005
14: (4, 2)	0,013	0,004
15: (4, 4)	0,012	0,004

Как видно из табл. 3, размытие датасета не принесло желаемого эффекта, а только увеличило величину средних ошибок. В дальнейшем планируется рассмотреть датасет, рассчитанный во внефокальной плоскости.

Ниже приведены примеры сравнения картин ФРТ, построенных по коэффициентам из датасета, и картин ФРТ, построенных по предсказанным нейросетью коэффициентам. Поскольку датасет с размытыми изображениями показал себя хуже, показаны примеры только с неискажёнными изображениями. Результаты моделирования, а также графики истинных и предсказанных коэффициентов представлены на рис. 3–5.

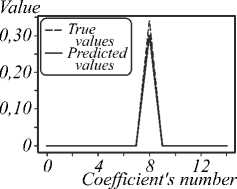
Рис. 3. Результат моделирования и коэффициенты для функции Цернике (n, m) = (3, 1) с коэффициентом b 3,1 = 0,336

Рис. 4. Результат моделирования и коэффициенты для функции Цернике (n, m) = (3, 1) с коэффициентом b 3,1 = 0,988

Value

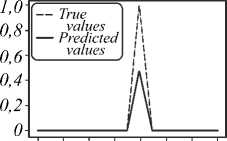
Coefficient's number

Рис. 5. Результат моделирования и коэффициенты для функции Цернике (n, m) = (4, – 4) с коэффициентом b 4,–4 = 0,683

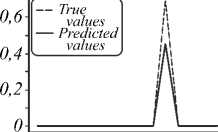
Coefficient's number

Как видно из приведённых результатов, обученная нейронная сеть удовлетворительно справляется с задачей классификации (определения типа), которая появилась вследствие специфически поставленной задачи регрессии. То есть, как правило, номер аберрации определяется верно, однако определение величины коэффициента происходит с заметными отклонениями. Наиболее очевидным способом решения этой проблемы является увеличение датасета. Кроме того, планируется рассмотреть датасет, рассчитанный во внефокальной плоскости.

Заключение

В рамках данной работы были смоделированы картины ФРТ в фокальной плоскости для когерентного случая и проведён процесс обучения нейронной сети для распознавания типа аберрации и её величины (коэффициента). Нужно отметить, что картины ФРТ в некогерентном случае, что более соответствует практическим приложениям исследования аберраций, будут иметь другой вид. Однако предлагаемый подход, основанный на обучении нейронной сети по некоторому набору картин, с этой точки зрения является универсальным, поэтому процедура в этом случае не изменится, хотя могут измениться результаты распознавания.

При обучении нейронной сети коэффициент обучения и количество эпох для датасета заданного размера был подобран эмпирически. Средние ошибки предсказания нейронной сети для каждого типа аберраций были получены для набора из 15 функций Цернике по датасету из 15 тысяч картин когерентных ФРТ в фокальной плоскости.

По результатам обучения можно сделать следующие выводы. Предсказание типа аберрации обеспечивается по усреднённым абсолютным погрешностям в диапазоне 0,012–0,015, что можно считать удовлетворительным. Однако предсказание коэффициента аберрации имеет заметные отклонения и требует дополнительных исследований.

Наиболее вероятным продолжением данного исследования является увеличение датасета и перенос процесса обучения на TPU для увеличения скорости обучения. Также планируется рассмотреть датасет, рассчитанный во внефокальной плоскости.

В дальнейшем будет решаться полноценная задачи регрессии для определения суперпозиции аберраций по картине ФРТ.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-2909054 в части, касающейся машинного обучения и нейронных сетей, а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части моделирования аберрированного волнового фронта и расчёта ФРТ.