Распределение комплексной амплитуды и интенсивности в трёхмерной фигуре рассеяния, формируемой оптической системой при осевом расположении точечного объекта

Глубина резко изображаемого пространства является одной из важнейших характеристик оптических систем, поскольку отражает допустимую величину сдвига вдоль оптической оси относительно плоскости фокусировки, при которой изображение все еще можно считать достаточно резким [1].

В настоящее время существует несколько подходов к количественной оценке глубины резкости оптической системы. Так, например, в традиционной оптике под глубиной резкости принято понимать такое смещение плоскости наблюдения изображения, при котором изображение точечного объекта, представляемое в виде геометрической точки, размывается в круг, диаметр которого равен диаметру центрального кружка картины дифракции Эйри. Выражение, позволяющее определить глубину резкости оптической системы в соответствии с этим критерием [2], имеет вид:

I b | = ± ( X n /2 A ² ), (1) где А ‒ числовая апертура оптической системы; λ ‒ длина волны используемого излучения; n ‒ показатель преломления среды (в случае воздуха n = 1).

В соответствии с выражением (1) изображение точечного объекта считается достаточно резким до тех пор, пока его диаметр не превысит диаметр первого минимума в картине функции рассеяния точки при отсутствии аберраций, то есть пока центральный максимум не сливается с первым кольцом [2, 3].

Однако очевидно, что далеко не вся энергия, прошедшая через оптическую систему, распределяется исключительно внутри области, ограниченной величинами, рассчитанными на основании выражения (1). Так, в работе [4] приведена другая формула, полученная на основании интерференционной теории формирования изображений:

|b | <<  2 X n / A 2 . (2)

Она не позволяет рассчитать глубину резкости, а лишь ограничивает сверху ее максимальное значение. Нетрудно заметить, что предельный диапазон сдвига относительно фокусного расстояния в этом случае отличается от величины, полученной в соответствии с выражением (1). В то же время, как следует из обеих формул, если считать длину волны неизменной, то на величину глубины резкости оказывает влияние фактически только один параметр – числовая апертура оптической системы.

Это является серьёзной проблемой при разработке оптических систем с максимально возможной глубиной резкости. В частности, при разработке оптических проекционных систем, предназначенных для работы при больших числовых апертурах в коротковолновых областях спектра. К таким системам, например, относятся фотолитографические проекционные объективы. Свойственные им малые глубины резко отображаемого пространства обуславливают необходимость обеспечения высокой точности позиционирования полупроводниковой пластины, на поверхности которой формируется изображение, что приводит к значительному усложнению и удорожанию фотолитографических проекционных установок.

В настоящее время известны различные методы, позволяющие увеличить глубину резкости. В некоторых из них предлагается использование дополнительных фазовых масок [5], модификаций оптических установок [6], особой цифровой обработки изображений на стадии их регистрации [7]. Однако эти методы слабо подходят для применения в фотолитографии – обработка изображений после регистрации в данном случае, очевидно, невозможна, а модификация проекционного оборудования дополнительно усложнит конст- рукцию и без того сложных фотолитографических объективов.

Метод, позволяющий обойти ограничения традиционных оптических систем, предложен в работе [8]. Он основан на замене традиционного проекционного объектива на синтезированную голограмму-проектор, формирующую требуемое изображение на поверхности полупроводниковой пластины. Причем синтез этой голограммы осуществляется в виртуальном пространстве, что позволяет использовать дополнительные корректировки формы представления объекта, недоступные для реализации в действительном физическом пространстве, например, в силу конструктивных ограничений установки для записи голограмм. Синтезированная таким образом голограмма при ее восстановлении формирует не одно, а сразу несколько параллельно расположенных на некотором заданном расстоянии друг от друга одинаковых изображений фотошаблона. Использование метода позволяет существенно увеличить глубину резкости изображения, проецируемого на поверхность полупроводниковой пластины. Синтез необходимой для его реализации голограммы требует применения такой объектной волны, которая фактически представляла бы собой суперпозицию нескольких объектных волн, формируемых одним и тем же заданным фотошаблоном при нескольких расстояниях между объектом и плоскостью синтеза голограммы, различающихся между собой на некоторую заданную величину сдвига Δ, не превышающую глубину резкости голограммы. При этом оптимизация величины сдвига, оказывающей существенное влияние на глубину резкости голограммы, невозможна без знания распределений комплексной амплитуды и интенсивности в трёхмерной фигуре рассеяния, формируемой оптической системой, роль которой в данном случае выполняет голограмма-проектор.

системы. Для простоты анализа ограничимся случаем одномерной голограммы.

Итак, пусть поверхность голограммы совпадает с осью X (рис. 1), где точка O является центром голограммы, а точкой F обозначено положение восстановленного с ее помощью изображения точечного объекта в плоскости наилучшей установки.

В этом случае в точке F интенсивность света в фигуре рассеяния будет максимальной, а величину сдвига фазы для этой точки можно принять равной 0. Определим для начала величины сдвига фазы и интенсивность в точке K , сдвинутой вдоль оптической оси относительно F на величину Δ.

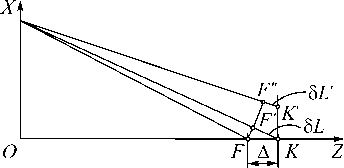
Рис. 1. Восстановление изображения точечного источника при сдвиге относительно плоскости наилучшей установки

Общая интенсивность света в точке K будет складываться как сумма комплексных амплитуд, приходящих от всех точек голограммы, возведённая по модулю в квадрат. Для расчётов выберем некоторую точку X , лежащую на плоскости голограммы. Поскольку мы условились считать суммарную фазу в точке F нулевой, то величина фазы во всех точках, лежащих на окружности с центром в точке X , будет одинакова. Соответственно, набег фазы в точке K относительно F будет зависеть от разности хода между лучами XK и XF' , иначе говоря [10]:

Ф = у-51 = "f-( XK - XF' ) = y-( XK — XF), (3)

где λ – рабочая длина волны; δ l – разность хода между лучами. В случае осевого луча она равна величине сдвига Δ, то есть расстоянию FK . Для других случаев величина разности хода будет определяться следующим образом:

51 = XK - XF == VOX2 + (OF + A)2 - VOX2 + OF2 =         (4)

= V OX ² + OF ² +A ² + 2 ■ OF -A -V OX ² + OF ² .

Это выражение также может быть дополнено для общего случая, когда точка K не лежит на оптической оси. В этом случае добавляется параметр KK' – величина вертикального сдвига, направленного перпендикулярно оптической оси. Тогда разность хода будет считаться, как:

I 5l' = XK' - XF'' = XK' - XF =

= V( OX - KK' ) 2 + ( OF + A ) ² - OOX² + OF².

Раскладывая выражение (4) в ряд Маклорена для квадратного корня [11], получаем:

5 1 = OF

(I 1 + 2X2 + 2 ^A . ^A J

V OF² OF OF²

- V 1 + OX ²/ OF²        ,

1 f OX ² 2 A A ² +1

2 1 OF ² OF OF ²

^^^^^^B

= OF ^

1 f OX ² 2 A A ² Y +   +

8 1 OF ² OF OF ² J

^^^^^^B

.

OX ² OX ⁴

- 1-- T +------7

2 ■ OF ² 8 ■ OF ⁴

После раскрытия скобок и упрощения выражение (6) можно привести к следующему виду:

5 1 = A- OF ^

A3 fi A ) 1 ++

2 OF ³ ( 4 OF J

OX2 ■Af,A )

+

2 OF ³ ( 2 OF J

При незначительных по сравнению с фокусным расстоянием системы величинах сдвига Δ значения сумм в круглых скобках приближаются к 1, что позволяет ещё более упростить выражение:

f A OX²    A³ ) _

5 1 = A — — +        =

( 2 OF ² 2 ■ OF ² J

- f, OX ²       A ² )

= A 1---- ^.

( 2 ■ OF ² 2 ■ OF ² J

Подставив (8) в (3), получим:

_ 2n_Af ₁_ OX ² _ a² )

= X ( 2 ■ OF ² 2 ■ OF ² J

2 n . f, OX ² )

A 1 —           .

X ( 2 ■ OF ² J

Если же мы хотим посчитать изменение длины пути и, соответственно, сдвиг фаз не относительно точки F , а с учётом разности хода для осевого луча, то из (8) нужно вычесть величину сдвига Δ:

5 1" = ( XK - ОК ) - ( XF - OF ) =

= XK - XF -A

fA OX 2 (T ■ OF ²

A 3   )

+

2 ■ OF ² J

^

A ox ² 2 ■ OF ² ,

ф " =

2 n A OX ² ------— .

X 2 OF ²

В случае, если сдвиг фаз φ'' принять равным 2π, то из выражения (11) можно вывести следующее равенство:

I A|

2 X^ OF²

OX ²

2 X       2 X

OX ²/ OF ² ~ Ac ’

где A – числовая апертура. Выражение (12) совпадает с формулой (2) для ограничения глубины резкости.

Как уже было сказано выше, результирующая комплексная амплитуда в точке будет равна сумме дошедших до неё комплексных амплитуд от всех точек голограммы. Поскольку в нашем случае речь идёт о синтезированных голограммах, имеющих дискретную структуру [12, 13], то количество этих точек конечно, а каждая из них фактически представляет собой отдельный точечный источник. Удобнее всего комплексную амплитуду от точечного источника рассматривать в виде вектора, длина которого соответствует амплитуде, а направление – фазе (рис. 2 а ) [14].

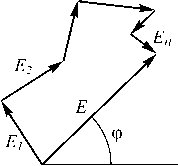
Тогда суммарная комплексная амплитуда в некоторой точке будет представлять собой векторную сумму амплитуд от разных источников (рис. 2 б ).

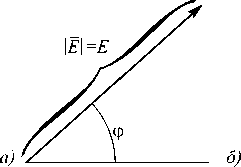
Рис. 2. Представление комплексной амплитуды в виде вектора: единичный вектор (а); суммирование комплексных амплитуд (б)

Далее остаётся найти распределение комплексной амплитуды восстановленной волны в каждой из точек от O до X . Отметим, что значения комплексной амплитуды симметричны относительно начала координат. Сделаем это в обратном ходе лучей, т.е. рассматривая процесс записи голограммы. Поскольку точечный источник распространяет свет во всех направлениях равномерно, исходящее от него излучение можно изобразить в виде сферы, центр которой совпадает по положению с рассматриваемым точечным источником. Тогда естественно предположить, что в единицу времени через поверхность сферы будет проходить одинаковое количество энергии.

Распространяющийся от точечного источника свет достигает плоскости регистрации голограммной структуры. Отношение между комплексными амплитудами в двух разных точках поверхности голограммы в рассматриваемом случае будет равно отношению площадей сфер S h и S l , на которых они расположены (рис. 3).

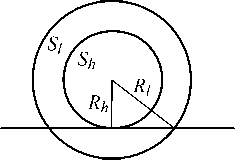
Рис. 3. Распределение комплексной амплитуды по плоскости от точечного источника

Отсюда следует, что в нашем случае, если комплексную амплитуду в точке О принять равной единичной величине E o , то амплитуда в точке X (рис. 1) будет равна:

e. = xSl

s _ 4 n R

S l 4 л- R

4 л- OF² _ OF² _    OF²

4 л- XF² " XF ² "  OX ² + OF²"

Таким образом, при помощи выражений (9) и (13) с использованием векторной суммы можно рассчитать значение комплексной амплитуды в любой точке на перпендикуляре, восстановленном из центра голограммы, а, возведя его в квадрат, получим значение интенсивности в выбранной точке.

Вычислить суммарную комплексную амплитуду в точке K можно через суммы проекций на координатные оси всех составляющих вектора суммарной комплексной амплитуды (рис. 2 б ). Если комплексную амплитуду от одной точки считать как E x , то её проекция на ось абсцисс будет считаться как косинус угла наклона вектора, равного сдвигу фазы, на ось ординат – как синус. В общем обе составляющие будут складываться из всех значений амплитуды и фазы, пришедших от каждой из точек, лежащих на плоскости от O до X :

E cos

I ^2п л I 1 _ > cos —A 1

A x — О      у        у

X X    I ^2П  I

E sin ^_ L ^sin l v^A l ¹ x _ 0     v ^A   v

x ²         OF²

2 - OF ² J J ^- x ² + OF² ’