Распределение концентрации смешивающихся компонентов в плоском диффузионном канале при произвольном перепаде давления на его концах

тов по длине диффузионного канала нелинейное. В настоящее время нет теории, позволяющей описать переход “диффузия-конвекция” при произвольном перепаде давления на концах диффузионного пути. В представленной статье рассматривается распределение концентрации смешивающихся компонентов по длине диффузионного канала.

Как и для бинарных смесей, процесс смешения в трехкомпонентной смеси сопровождается диффузионным бароэффектом [5]. Для вязкого режима величена отношение перепада давления меджу концами диффузионного канала и давле- ния в системе –

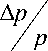
имеет порядок Kn2 и яв- ляется пренебрежимо малой, поэтому бароэффект обуславливает выполнение условия:

to — с и 1 + с 2 и 2 + с 2 и з — 0 ,        (1)

где с_i - концентрация i -го компонента.

Диффузионные скорости компонентов u _i определяются из уравнений Стефана-Максвелла [6]:

сс3 u - r )+ с1с2 u - r )— -V с

D13

сс- ⁽ r ^- u ) +     ^{( и}2 ^- r ^)—-V с 2 . (2)

D12

Используя уравнения (2), определение для r n1 U1 + n 2 й2 + n 3 U13 среднечисловой - to — и n

r среднемассовой - ио

р 1 Ш 1 + р ₂ и₂ + р ₃ й ₃

ско

Р

на настолько, что время поперечного выравни-

² r вания концентрации ^Tr /D. мало по сравне-

нию со временем движения смеси вдоль канала

L

^T L = ---

U 0 z

L ²

^(А p ^- p g z L ) -8 п

ростей, плотность компонента - p i = с m i ( m i -масса i -го компонента), получим систему уравнений, описывающей макроскопическое движение трехкомпонентной газовой смеси:

1     8kT где п = — рЛ. ---

2     п т

D_i – истинный коэффици-

ент диффузии. Из условия T _r << Т _L легко получить следующие ограничения на А p :

Р

u+(иЖ д It

= -V p + п Аи _о +

у + § V div i r o + pg ’

^ 1 + o V с 1 = div ( D ^V с 1

⁺ D j2 ^V с 2 ) ,

с^ + + 3V с. = div ( D^ ', V с + D ,' V с ,)

2               21     1        22     2 , д t

д n д t

- n dive r ,

где g - ускорение силы тяжести, п и § — коэффициенты сдвиговой и объемной вязкости, D_ij – матричные коэффициенты многокомпонентной диффузии, определяемые через коэффициенты взаимной диффузии D_ij следующими соотношениями [6]:

* _ ^D 13 ^{[ с} 1 ^D 23 ^{+ (} с 2 ⁺ с 3 ) D 12 ^]

■D 11

^С 1 ^D 23 ⁺ с 2 ^D 13 ⁺ с 3 D 12

D

*

^С 1 ^D 23 ⁽ D 12   ^D 13 )

^С 1 ^D 23 ⁺ с 2 ^D 13 ⁺ с 3 D 12

^D 23 ^[ с 2 ^D 13 ^{+ ( с} 1 ⁺ с 3 ) D 12 ^]

^С 1 ^D 23 ⁺ с 2 ^D 13 ⁺ с 3 D 12

D

*

с 2 ^D 13 ⁽ D 12   D 23 )

^С 1 D 23 ⁺ с 2 ^D 13 ⁺ с 3 D 12

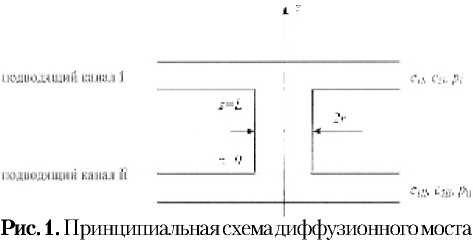
Рассмотрим движение тройной смеси в вертикальном плоском канале с длиной L и полушириной r, ось z направлена вдоль оси канала вверх, рис. 1. Будем считать, что rL <<  1 , разность давлений на концах канала A p ограниче-

Аp - pgzL    Л L2 ^ Аpбар LL p           r2 r2 p r2

или

А p - p g z L r ² r ² p     Л ² L 2

<< 1 , где Л — длина свободно

го пробега молекул, А p _бар - величина диффузионного бароэффекта. Если наложенные ограничения выполняются, то в поперечном сечении успевает сформироваться определенный, почти однородный состав. В соответствии с условиями поставленной задачи силы V p и p g ^r действуют только в направлении оси z , поэтому будем принимать во внимание только проекцию уравнения Навье-Стокса на ось z , которая может быть записана так:

dUz   I   д и

^0"+p| и о -    +и д t      I      дх

5 и, З и ,)

---0^ + и_П7 ---0 z

0z              0z ду         с.z у

дp     д 2 u_z

— + п  0^ д z    ^ д х ²

+ п ^Гд Ц о х 3 д z ( д х

, д ² и о z д У ²

! ^ди о У

д У

д ² и ₀ z

⁺ д z ² _v

+5 ^ 0 ^ )

д z >

+

⁺ pg z .

Отношение инерциального члена к вязкому члену можно оценить так:

9Uz pu о z ^z oz_ д 2U дх

r ² r ² А p - p g _z L

1У L ²    p

но в соответствии с наложенными ограничениями на А р это отношение много меньше единицы, поэтому инерционными членами можно пренебречь. В вязком члене, очевидно, можно пренебречь продольной производной, так как

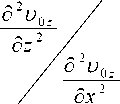
отношение.

r 2                 _r

Ly . Член с div u ₀ дает такое же

Опуская малые члены, вместо (4) имеем:

du dp p—— + — = n dt    dz

22 ---0 z + -— 0z-

( 5 x ²     5 y ² J

+ P g z . (5)

Перейдем к анализу уравнений непрерывности и конвективной диффузии системы (3). В процессе конвективного течения в вертикальном длинном канале вдали от торцов можно принять, что to _x = to y = 0 . Запишем более подробно правую часть уравнений диффузии:

Рассмотрим теперь стационарное смешение при отсутствии свободной конвекции, но учтем, что при этом возможно наличие вынужденной конвекции, реализующейся под действием разности давлений на торцах вертикального канала. Это соответствует условиям наблюдения смешения в установках диффузионного моста, в которых вертикальный канал омывается на его концах смесями газов с поддержанием фиксированных значений как разности концентраций, так и разности давлений. Учитывая стационарность процесса, вместо (5) имеем:

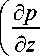
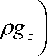
= П ^A y ^u о z .

div ( D 1*1 V c 1 + D*, V c ₂ ) =

Решение уравнения (9) , соответствующее независимости ^d p / z и pg z от поперечной координаты, имеет следующий вид [7]:

d d x

_ * ^d c i

^D 11^ ^{+ D} 12

d x

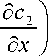
d

+ — d y

d y

+ D

*

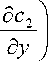
( х ² - R ² ) (d p      )

^и о z = л-----I д P ^gz I 4 n v d z       J

+

_ст(и)D  ^£1. -^(^)Р)  Ёсу.  , и13 D13       ° 23 D 23

д z            д z

d

+ — d z

( D 11

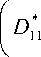
*1 + D dz

*

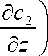
где a^ ) , ^ 2 з — константы диффузионного

так как c ₁ и c ₂ слабо зависят от поперечных координат, то (6) можно переписать в виде:

скольжения для среднемассовой скорости, кото рые отражают тот факт, что скорость и _0z на бо ковой границе канала равна скорости диффузи онного скольжения.

-

-

-

div ( D 1*1 V с 1 + D 12 V с ₂ ) = = D ^A ^ с 1 + D *₁₂ A_± с ₂ +

Интегрируя этого выражения по площади сечения канала, получим:

d

+ — d z

d с

^D 11^ ^{+ D} 12 d z

д с ₂ ) d z J ,

^u о z

-

r

d p

-

8 n Vd z

P g z

-

где A_± с 1 =

d ² с 1 d ² с 1 d x ² d y²

Учитывая условие to x = to y = 0 и (7), перепишем уравнения диффузии для условий нашей задачи с учетом пренебрежения малыми величинами:

^d с 1        ^d с 1    n* A n* A

+ to_ ----= D i i A . с + D i ₉ A । с ₉ +

, z               11 ^ 1        12 ^ 2

d t      оz d ( dс      dс2 3

+ —I D _n—¹ + D _n—²- I

11               12

оz \    оz       оz J

,

^д с 2         ^d с 2       * a ri* A

——- + toz — = D 21 A± с 1 + D 22 A± с 2 + о t      оz d ( _ * dс       dс2 3

+ —I D₂₁ —1- + D„ —²- I

21             22

оz \    оz       оz J

,

- ° 1 U ) D 13

d c 1 d z

- ° 2 U ) D 23

d c ₂ d z

С учетом соотношения между u ₀ и to e виде u ₀ — to = D 1 V c 1 + D ₂ V c ₂ , для среднечисловой скорости можно записать:

^to z

r ² ( d p

8 p V d z

° 13 ^D 13

d c 1 d z

P g z

° 23 ^D 23

d c ₂ , d z

где ° ₁₃ , ° ₂₃ - константы диффузионного скольжения для среднечисловой скорости.

Вместо (8), усредняя по сечению канала и учитывая стационарность процесса, имеем:

^to z

to _z

dn    dto

— = n—- . d t      d z

d c 1 d z

d c ₂ d z

^toz = 0 dz

—I D *

d z V    ¹¹

5 c L + D dz

— ⁽ _D *

6 z V ²¹

dc, —1- + dz

.

*

d c ₂ | d z J ,

D ₂ * ₂

d c ₂ । d z J ,

Так как в соответствии с уравнением непрерывности в (10) to_z не зависит от z , то прямое однократное интегрирование уравнения диффузии по z дает:

* 5 c i     * 5 ^- 2

to.- — D     — D— z 1        11                121 dzd

* 5 c i     * 5 ^- 2

®z- 2 - D 21      D 22^ — Q 2 ,(11)

oz       оz где Q1 и Q2 - некоторые константы, независящие от z и имеющее физический смысл парциальных плотностей объемного потока первого и второго компонентов.

Рассмотрим систему уравнений (11) для случая малых концентраций самого тяжелого компонента. В этом случае выражения для матричных коэффициентов диффузии упрощаются, и мы получаем следующую систему уравнений для парциальных плотностей объемного потока компонентов:

Решение дифференциальных уравнения (12) с граничными условиями, поставленными в соответствии с устройством диффузионного моста, ^- i^{(0) — -} i ii , ^- 2 ^{(0) — -} 2 ii , ^- i^{( L} ) ^{— -} i I , с ₂ ( L ) — с ₂ I ; p ( L ) — p_n ; p (0) — p I , рисунок 1, имеют вид:

с i ⁽ z ^{) —} с i ii exp

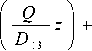
f

⁺ C 1 i ^- с 1 ii exp

k

^C 2 i ^{- C} 2 ii exp |

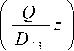
Q^ l

D 23 D 13

C 2(z)—-------7---------- i I Qv     I

1-exp l          z I +

DO k 23 13 J

Sc.

Q. — Q-. — D   -¹1            1         13           ;

о z

I Q t    I

^{+ C} 2 ii p | "тТтГ² I , k ^D 23 D13 J

Q 2 — Q- 2 + - 2

D 13 ( D 12 - D 23 ) 8 - ,

- 1 D ₂₃ + - ₃ D 1 ₂   5 z

^^^^^^^^

D 23 D 12     5 - 2

^- 1 ^D 23 ^{+ -} 3 D 12 ^{9 z .}

1 - exp I ------z I k D13 J

1 - exp f I k D13 J J

f Qv |      g)„

1 - exp|        z I +        ------x k D23 D13 J D23 D12 - VD13

I I Qv     I I Q x| exp |     —z I- exp I ^^z л n D k k 23 13 J k 13 ,

D ^D 23 ^D 12 ^{- V} D 13

I Qv J I Q т expl       L I-expl L—L n n       Л k 23 13 J k 13 ,

+

I Q J C11   C1 ii exp I d L I где v — D12 - (D12 - D 23 )----------f     13|—

1 - exp I - Q- L I k D 13    J

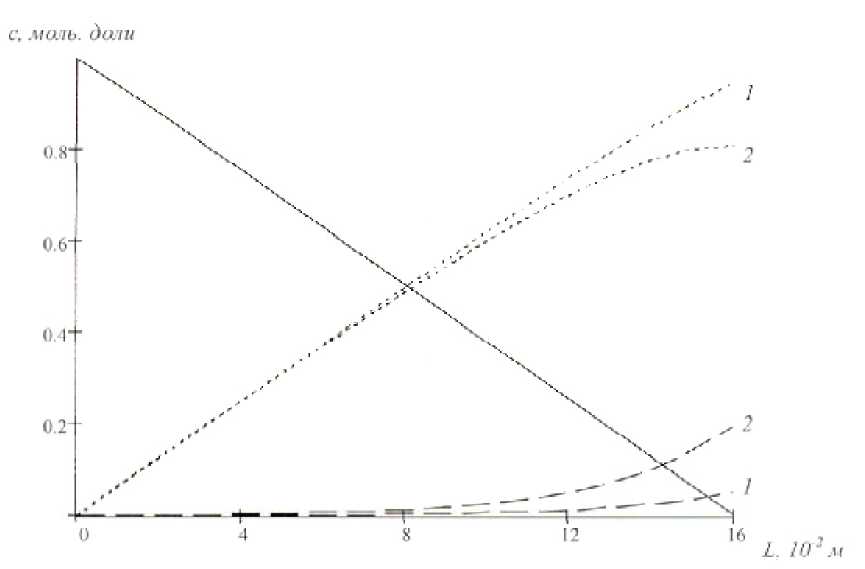
Рис. 2. Распределение концентрации о длине диффузионного канала: сплошная линия – аргон; пунктирная линия – фреон-12; линия из точек – гелий. 1 – система 0,046 Fr₁₂ + 0,954 He – Ar ; 2 – система 0,194 Fr₁₂ + 0,806 He – Ar

и

5 = (D 23

D)

^с 1 II - ^с 1 1

Г Q ^

¹ - exp ^L

V ^D 13 7

тяжелого компонента смеси получено решение для распределения концентрации по длине диффузионного канала, которое нелинейно, по мере уменьшения содержания тяжелого компонента приближается к линейной.

В случае малости потока Q « 0 , для газовой системы Ar – He + Fr₁₂ на рис. 2 представлено распределение концентрации гелия и фреона-12 по длине диффузионного канала L=0,16 м .

Нетрудно заметить, что для системы гелий-+фреон-12 – аргон, в которой выполняется условие D 12 , D 13 >  D ₂₃ , имеет место нелинейное распределение концентраций по длине диффузионного канала. С уменьшением начальной концентрации тяжелого компонента (фреона-12) в бинарной смеси распределение концентрации становится линейным. Мы считаем, что нелинейное распределение концентрации способствует образованию конвективного массопереноса недиффузионной природы.

В заключение сформулируем некоторые выводы. Получена система одномерных (усредненных по сечению диффузионного канала) уравнений локальной неравновесной термодинамики для описания неизобарного смешения тройных газовых смесей в вертикальном канале. В приближении малых концентраций самого