Распределение нагрузки в коническом подшипникекачения

Распределение нагрузки по роликам определяется с учетом совместности деформаций и перемещений колец. Для расчета перемещений колец примем систему координат, приведенную на рис. 1.

Начало координат совместим с вершиной конуса беговой дорожки внутреннего кольца.

В принятой системе характерные точки торца ролика будут иметь координаты:

Х а = d F /2 1д в и y А = d F /2 - для контакта с внутренним кольцом;

Хв = dp /2tgP — Dw sin Y и У В = dF /2 + Dw cos Y — для контакта с наружным кольцом.

Центр тяжести ролика будет иметь координаты:

х о = D о/² tg Y и У о = D о/².

В рабочих условиях при изменении размеров колец вследствие теплового и центробежного расширения, а также деформаций от посадочных натягов координаты характерных точек ролика определятся по формулам:

хАр = dFp /2 tge, У Ар = dFp /2 , хВр = dFp 2 tge - Dwp sin Y,

УВр = dFp /2 + Dwp cos Y, х0р = Dор /2tgY и yор = Dор /2 .

При нагружении подшипника радиальной и осевой нагрузками будет происходить смещение колец. Принимаем, что смещения колец опреде-

ляются как смещения вершины конуса беговой дорожки наружного кольца относительно вершины конуса внутреннего. При изменении размеров колец произойдет относительное смещение вершин конусов внутреннего и наружного колец, как показано на рис. 2.

В принятой системе координат при отсутствии деформации в контактах координаты точки контакта большего торца ролика с наружным кольцом определятся по формулам:

xB = xAp — Dwp sin Y

И У в = ^dFp /^{2 + D}wp cos Y .

Величина смещения вершины конуса наружного кольца относительно конуса внутреннего определится выражением:

^ о = ^х в - Уврд ^а .

С учетомсмещений колец координаты характерных точек ролика в зависимости от его углового положения будут определяться по формулам:

хАр (i )= dFр /2 tge , У Ар (i )= d Рр /2 , хо р (i ) = Dо р/2 tgY и У о р = Dо р/2 .

Координату точки В на наружном кольце определим как точку пересечения двух прямых:

У = ( x - S a ) • tga - S r cos ( ^ + п ) - для образующей конуса наружного кольца и У = У ар ^{( i} ) ^{- ( x - x}Ap ^{( i} ^Z tg Y — проходящей через точку A по нормали к оси ролика.

Здесь S_a и S_r – соответственно осевое и радиальное смещения наружного кольца.

Угловая координата i -го ролика определится от линии действия радиальной нагрузки по

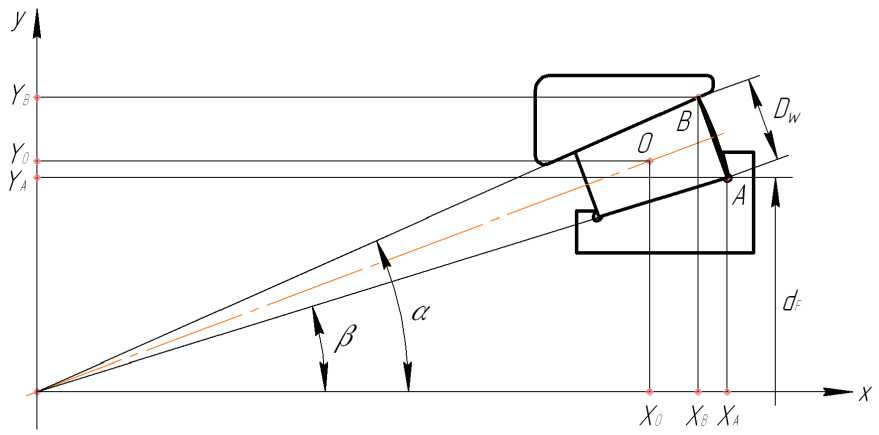
Рис. 1. Начальная система координат подшипника

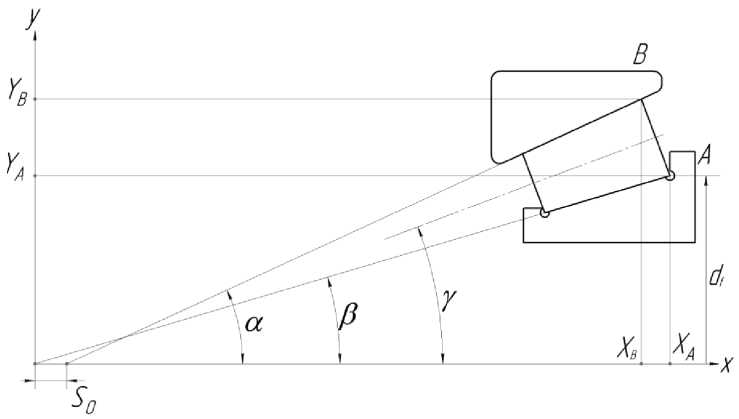
Рис. 2. Начальное смещение колец

формуле ф = 2п ( i - 1 )/ z .

Из решения приведенной системы уравнений найдем координаты точки В :

⁽ x Ap ^{(i )+ (} У Ар (i ^{) + S} a tg ^{a + S} r cos ^^gY ) ( 1 + tga- tgy )

х вр ( i )

и У Вр ^{( i} ) = ⁽ x Bp ^{( i} ) — S a У tg ^{a -} S r .

Координаты характерных точек определяют положение зоны контакта каждого ролика с бего- выми дорожками внутреннего и наружного колец.

Кроме того, расстояние между точками А и В определяет наличие – отсутствие контакта ролика с внутренним кольцом. При этом, если получим ^(хАр (i) - xBp(i))2 + (Увр (i) - УАр (i))2 > Dwp, отсутствует контакт ролика с внутренним кольцом.

При расчете усилий взаимодействия роликов с бортиком внутреннего кольца принимаем, что точка контакт торцов роликов с бортиком находится в средней части по высоте бортика. Тогда получим координаты точки контакта:

^х б ^{( i} ) = х Ар ^{( i} ) ^{- (} d бр ^- d Fp ) tg Y/ ⁴

и У бр ^{( i} H d бр ⁺ d Fp )/⁴ .

Под действием гироскопического момента происходит перекос ролика относительно беговой дорожки кольца. В этом случае расчет распределения нагрузки по линии контакта выполняется по аналогии с методикой работы [3].

При известном значении усилия F в контакте, перекосе ψ ролика и координатах начала x ₁ и конца x ₂ зоны контакта определяется начальное значение деформации в контакте по известной формуле [4]:

5 0 = 8 ■ IO ^-5 F ^0,9 /( ( x 1 - x ₂ )/cos a )^0,8 — для контакта с наружным кольцом;

5 0 = 8 ■ 10 ^-5 F ^0,9/ ( ( x 1 - x ₂ )/cos в ) 0^ — Для контакта с внутренним кольцом.

Линию контакта разбиваем на 20 участков. Длина каждого участка будет равна А х = ( х 1 - х ₂)/ 20 .

Координаты центра каждого участка будут равны:

x j = x 1 - А х ■ ( j - 0,5 )

и yj = (xj - Sa) ■ tga - Sr cos ф - для контакта с наружным кольцом, xj = x2 + Ax ■ (j - 0,5) и yj = xj ■ tge - для контакта с внутренним кольцом.

Здесь: S_a и S_r – осевое и радиальное смещения вершины конуса наружного кольца.

Принимая для 1-го участка величину контактной деформации равной δ ₀ , величины деформаций для каждого участка с учетом перекоса ролика определятся по формуле:

б х = 5 0 - у • ( х 1 - хj )/ cos у — для контакта с наружным кольцом;

б х = 5 о - у • R Х 2 - х j )/ cos у - для контакта с внутренним кольцом.

При δ _х ≤ 0 нагрузка на данном участке принимается q ( j ) = 0.

При положительном значении деформации определение нагрузки для каждого участка определяется методом простой итерации [5].

В качестве начального приближения принимаем q ₀ = F /20 . По формулам работы [6] определяем ширину площадки контакта:

b = 2 ^q ₀ • пR_np ^cos а ( n ^A x ) - для контакта с наружным кольцом;

b = ²^ q 0 • q R. cos в Rx -b x ) – для контакта с внутренним кольцом.

Здесь: п = П к ⁺ R w . где П ^ = ( 1 - e w )/ E w ^- для ролика, п _к = ( 1 - е „ ²)/ Е_в - для внутреннего кольца, п _к = ( 1 - е Н )/ Е н - для наружного кольца.

Приведенный радиус кривизны в контакте определится отношением:

R пр = R w R R RR + R w ) — для контакта с внутренним кольцом;

R пр = R_w R R RR - R w ) — для контакта с наружным кольцом.

Радиусы поверхностей роликов и колец в каждом сечении определятся выражениями:

R_w = D_Wj /2cos а и R = xtga/ cos а — для контакта с наружным кольцом;

Rw = Dw,j (2 cos в и R = х tgP/ cos в — для контакта с внутренним кольцом.

Диаметр ролика в данном сечении определится по формуле:

D w = D wp ^{- 2 ( x}Ap ^{( j} )^- x j ) tg ^ w /^cos у — в контакте с внутренним кольцом;

D wj = D wp ^{- 2 ( х}вр ⁽ j )^{- x} ) ^t g Ф w /^cos У — в контакте с наружным кольцом.

Здесь ϕ _w – угол конуса ролика, определяемый как ф ^ = ( а - в )/ 2 .

После определения ширины площадки контакта находим следующее приближение величины нагрузки:

q ( j ) = ( б _х A x П 2cos a)/Rk _w + к ) - в контакте с наружным кольцом;

q ⁽ j Ы ^б х A x ^{П 2cos} P )R ^kw ^{+ к} ) –в контакте с внутренним кольцом.

При этом: к _ад = q w • ln ( 2 R w/ b ) + 0,407 и к = п_к • ln ( 2 R/b ) + 0,407.

Если не обеспечивается с заданной точностью условие q (j) « q0, принимаем q0 = q(j) и расчет повторяется. При выполнении заданной точ- ности проверяется условие равновесия:

Z q ( j ) = F .

j = 1

При невыполнении условия равновесия вводится поправка в значение величины δ ₀ и расчет повторяется.

После определения нагрузок на каждое сечение вычисляются значения напряжений на каждом участке:

^ Н ⁽ j ) = д/ q ⁽ j ) cos aRn^- q • Rnp • A x ) - в контакте с наружным кольцом;

ст₆ ⁽ j ) = ^q ⁽ j ) cos pRn • q • R np • A x ) - в контакте с внутренним кольцом.

При неравномерном распределении нагрузки по линии контакта на ролик действует опрокидывающий момент:

20 М = Z ( q ( j ^ l ) . j = 1

Здесь l – эксцентриситет нагрузки в данном сечении относительно центра тяжести ролика.

На рис. 3 приведена схема определения эксцентриситета нагрузки для контакта ролика с наружным (а) и внутренним (б) кольцами.

Линия действия нагрузки в данном сечении описывается уравнением:

x + y ■ tg a - ( x j + y j ■ tg a ) = 0 .

По рекомендациям [7] расстояние от точки О ( х о , У о ) до линии действия нагрузки определится по формуле:

¹ н = ^{( x} j ^{- x} 0 ^{+ (} У, ^- У 0 )f g ^a У V ^{1 +} tg ^a .

Для нагрузки в контакте с внутренним кольцом величина эксцентриситета определится по формуле:

l e = ^{( x} j ^{- x} 0 ^{- (} У 0 ^- У j ^g ^p У V ^{1 +} tg ^p .

Координаты центра тяжести находятся из выражений:

x0 =(xAp + xBp У2 - lw0p • cos У и У0 = (Уар + Увр У2 - lw0 p • sin У .

При этом координаты контакта торца ролика с внутренним кольцом x_Ap и y_Ap определяются, как показано ранее. Координаты контакта торца ролика с наружным кольцом определяются для каждого ролика по формулам:

= ^{( x}Ap ^{+ (} У ар ⁺ S a tg ^{a +} S r c^os Ф ) • tgy )

^{вр                 (} 1 + tga • tgy )              ;

У Bp = ^{( x}Bp ^- S a ) • tg ^{a -} S r ^cos Ф .

При отсутствии контакта с внутренним кольцом ролик прижимается к наружному кольцу центробежной силой F_c . Величина центробежной силы определяется, как показано ранее. Координаты торца ролика в этом случае показаны на рис. 4.

Значения координат х_Вр R i ) и У _Вр R i ) точки В торца ролика определяются по приведенным выше формулам.

Схема нагрузок на ролик приведена на рис. 5.

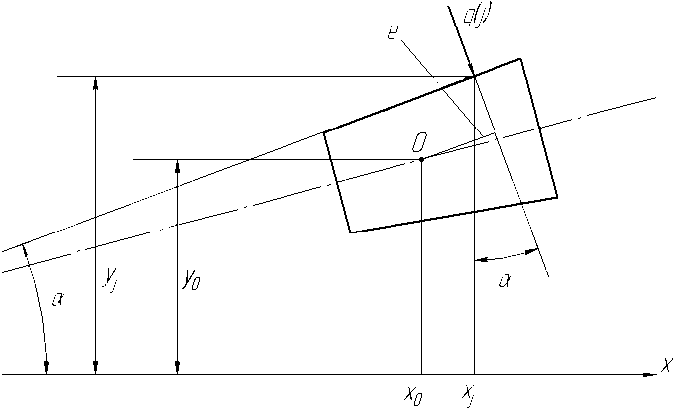
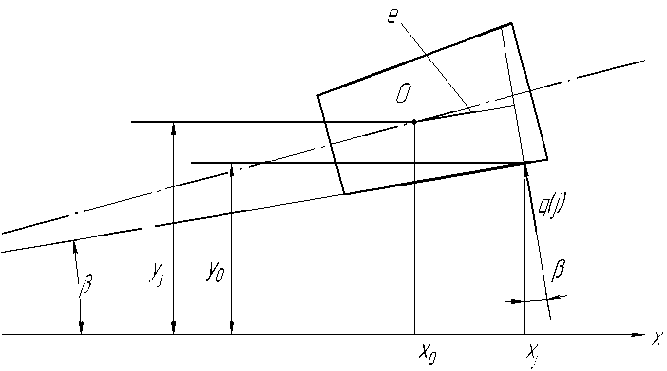
Рис. 3. К определению эксцентриситета действия нагрузки

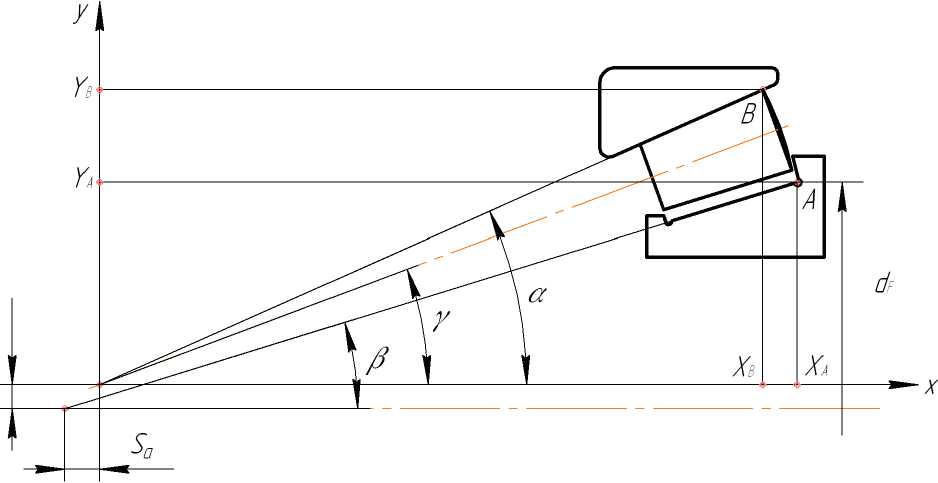
Рис. 4. Координаты торца ролика при отсутствии контакта с внутренним кольцом

Условия силового равновесия показаны на рис. 6. Соотношения сил определяются из выражения:

F6 =   Fh    =       Fc sin a sin (О - в) sin (n - (a + 0 - в)).

Отсюда получим:

F _h = F c sin ( 0 - в )/ sin ( a + 0 - в )

и F₆ = F c sin a /sin ( a + 0 - в ) .

Условия равновесия ролика под действием моментов, приведенных на рис.3, имеет вид:

£ ( q н ( j )Ц. ) - М г - F 6 i ₆ = о .

j = 1

Под действием сил и моментов происходит перекос ролика относительно кольца на угол ψ . Распределение нагрузки q_H ( j ) и эксцентриситет ее относительно центра тяжести ролика определяются, как показано ранее. При этом координаты начала и конца рабочего участка линии контакта ролика с наружным кольцом определяют-

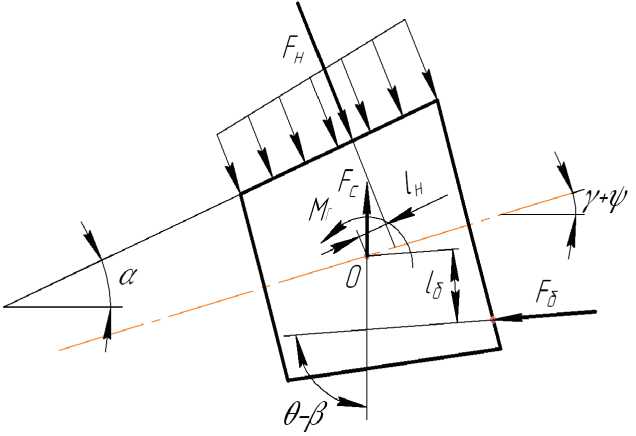
Рис. 5. Нагрузки на ролик при отсутствии контакта с внутренним кольцом

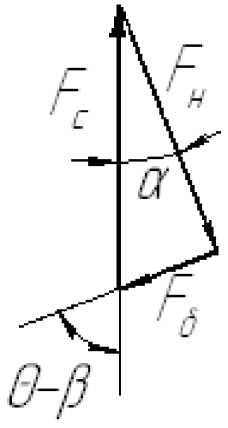
Рис. 6. Схема силового равновесия ролика без контакта с внутренним кольцом

ся по формулам:

X = Х вр ⁽ j ) ^-А " cos Y и х 2 = х Вр ( j ) — ( l w ^-A i ) • ^cos Y .

Здесь Δ и Δ ₁ – величины фасок соответственно у большего и меньшего торцов ролика.

Величина гироскопического момента М_г определяется ранее приведенными зависимостями.

Эксцентриситет l_б усилия F_б , действующего в контакте с бортиком, определяется по аналогии с ранее приведенными зависимостями по формуле:

, ₌ ^{( х}б ^- x 0 ^{+ (} У 0 ^- У б 'tg ⁽ 9 - ^{в )} б"         VI + tg ( е - в )         .

При этом координаты точки приложения усилия F_б определим приближенно:

х б = х Ар ( ^j ) - ( d бр - d Fp ^{)( 4t}g к ⁹ - ^в ))

и У б =^{( d} бр ^{+ d} Fp )/⁴ .

Определение угла перекоса ролика и связанного с ним распределения нагрузки по линии контакта определяется из решения с заданной точностью методом хорд [5] уравнения:

После завершения расчетов проверяется отсутствие контакта ролика с внутренним кольцом по условию:

V⁽ х Ар ^{( i} ) - х Вр ^{( i ) ) 2 +(} У вр ^{( i} ) - У Ар ^{( i ) ) 2} ^ D wp - 5 о .

При невыполнении приведенного условия необходим расчет ролика в нагруженной зоне при наличии контактов с двумя кольцами.

В нагруженной зоне ролик имеет контакты с внутренним и наружным кольцами. Схема кон- такта и координаты характерных точек ролика для этого случая приведены на рис. 7.

Значения координат х_Ар ( i ) , х_Вр ( i ) и у_Ар ( i ) ,

У Вр ^{( i} )

точек А и В торца ролика определяются по приведенным выше формулам.

Схема нагрузок на ролик приведена на рис. 8. Условия силового равновесия показаны на рис. 9.Уравнения равновесия ролика будут иметь вид:

F_H sin а - F_B sin в- F₆ cos ( 9 - в ) = 0 ;

F_H cosa - F_B cos в + F₆ sin ( 9 - в ) = F_c ;

Ф 1 ( г ) - S ( я- ( j ) l н ) - М г - F₆1₆ = 0 .

м н - M в + F₆1 б - M г = 0 .

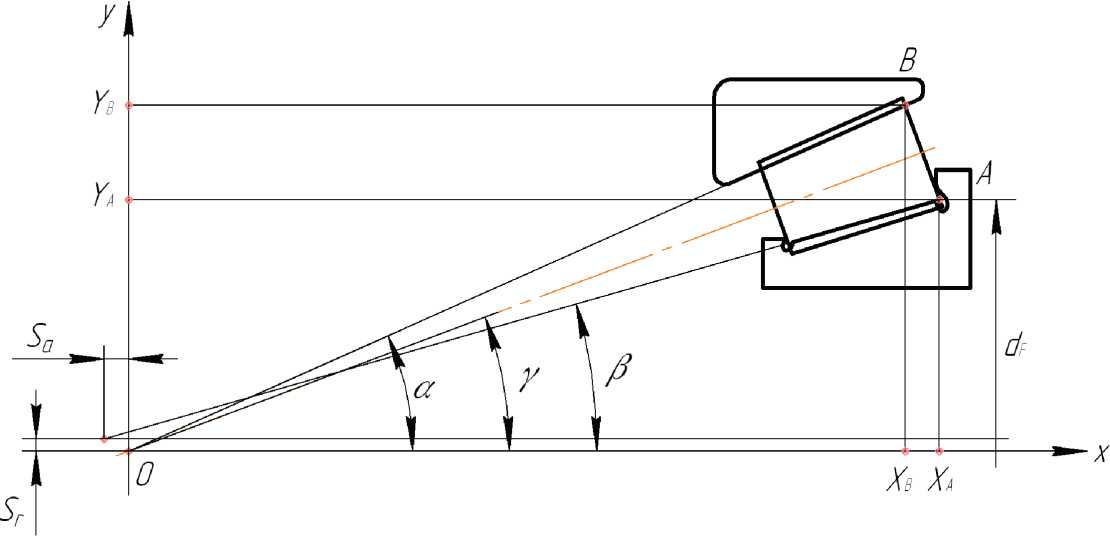
Рис. 7. Координаты торца ролика в нагруженной зоне

Распределение нагрузки по линиям контакта с наружным и внутренним кольцами, а также опрокидывающие моменты М_н и М_в являются функциями угла перекоса ψ ролика относительно колец. Расчеты распределения нагрузки и опрокидывающих моментов выполняются, как показано ранее. При этом координаты начала х ₁ и конца х ₂ линии контакта ролика с беговой дорожкой наружного кольца определяются, как показано в предыдущем разделе. Координата начала х ₁ и конца х ₂ линии контакта ролика с беговой дорожкой внутреннего кольца определяются по формулам:

х 1 = х Ар ⁽ j ) - ^А в • cos Y

И х 2 = х Ар ⁽ j ) — ^{( l}w ^-Д 1 ) • cos Y .

Здесь: А _в = А , если Д >  m , или А _в = m , если Δ < m , где m - длина выточки у основания упорного бортика.

Приведенная система уравнений не имеет аналитического решения. В связи с этим разделяем ее на две части. При предварительно заданном значении угла перекоса ролика у = 0 усилия в контактах определяются методом итерации. Определяется максимальное значение суммарной деформации в контактах по формуле:

⁵ = D wp ^- V⁽ х Ар ⁽ i ) — х Вр ⁽ i ^{) ) 2 + (} У ВР ⁽ i ) — У АР ⁽ i ^{) ) 2} .

Принимается начальное значение усилия F_в в контакте с внутренним кольцом. При i = 1 можно принять F . 0 = 4,6 P 0 ( Zz • cos a ) , где z - число роликов, а P ₀ – приведенная статическая нагрузка на подшипник, определяемая по [3]. При расчете роликов с i >1 можно принять F . о ( i ) = F . о O' " 1 ) .

Вычисляются:

F ( i ) = ⁽ F . о sin ⁶ + F sin W ^{- e} )) н          sin ( 6 - a - в )       ;

F6(i) = (Fh (i)sin a " F.о sin в)/sin (6 - в).

Рассчитываются соответствующие полученным значениям нагрузок распределения нагрузок по линиям контакта, величины опрокидывающих моментов во внутреннем М_в и наружном М_н контактах, а также максимальные значения контактных деформаций δ в и δ н . Если с заданной точностью 5 . + 5 н ~ б ^ , принимается F . ( i ) = F . 0 . В противном случае вводится уточнение F . о = F . о • б , /( б , + б _н ) и расчет повторяется.

Определение угла перекоса ролика и связанного с ним распределения нагрузки по линиям контакта ролика с внутренним и наружным кольцами определяется из решения с заданной точностью методом хорд [5] уравнения:

20 20

ф 2 ( у ) - S (q, ( j ) 1 н ) - S ( q . ( j 1. ) - М г - f « i « = ° . j =1 j =1

После завершения расчетов проверяется отсутствие контакта ролика с внутренним кольцом по условию:

V⁽ х Ар ⁽ i ) - х Вр ^{( i} ) ) 2 ^{+ (} У вр ^{( i} ) ^- У Ар ^{( i} ) ) 2 ^ D wp ^{- б} н .

При выполнении приведенного условия необходим расчет ролика при отсутствии контакта с внутренним кольцом.

Под действием нагрузок происходит смещение наружного кольца относительно внутреннего. Под осевым S_a и радиальным S_r смещениями понимаем отклонения вершины конуса беговой дорожки наружного кольца относительно вершины конуса беговой дорожки внутреннего кольца.

При изменении размеров колец произойдет вследствие теплового и центробежного расширения относительное смещение вершин конусов внутреннего и наружного колец. Величину начального относительного смещения S ₀ опреде-

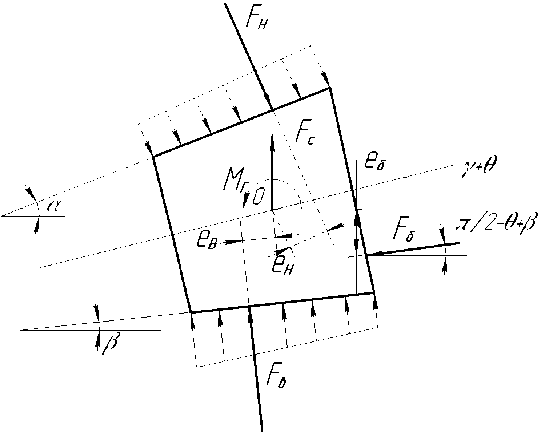
Рис. 8. Нагрузки на ролик при контакте с внутренним и наружным кольцами

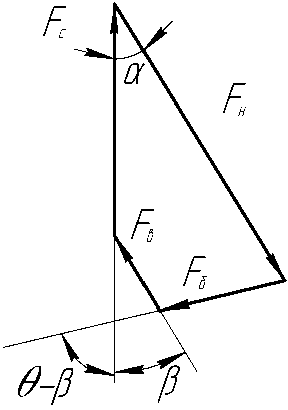
Рис. 9. Схема силового равновесия ролика при контакте с внутренним и наружным кольцами

лим, как показано ранее.

Величины смещений определяются условиями равновесия наружного кольца:

z

Ф а ( S a , S r ) - F a — S ( F . ( < >Ь « ) ;

= 1

z

и Ф r (Sa , Sr ) - Fr -S (Fh (i )cosacos Ф) .

i = 1

Решение приведенной системы уравнений выполняется методом Ньютона [4]. При этом частные производные функций Фа (Sa,Sr) и Ф, (S„, S„) по S„ и S заменяем отношениями ra r a r приращений.

Усилия в контактах роликов с наружным кольцом при заданных величинах смещений S_a и S_r определяются, как показано в предыдущих разделах.

На базе изложенной методики расчета разработана компьютерная программа, с помощью которой проведен пример расчета однорядного конического подшипника 6-7821К1, установленного в опоре главного редуктора.

Условия работы подшипника:

• -    радиальная нагрузка F_r = 18,05 кН;

• -    осевая нагрузка F a = 29,2 кН;

• -    частота вращения внутреннего кольца n = 4000об/мин;

Динамическая грузоподъёмность подшипника [8] С = 303,8 кН, статическая С0 = 434,3 кН. Габаритными размерами подшипника: внутренний диаметр d = 105 мм; наружный диаметр D = 180 мм; монтажная высота т = 49 мм.Ши-рина наружного кольца С = 39 мм, угол конуса беговой дорожки a = 14045', минимальный диаметр беговой дорожки DE = 148,634мм.Ширина внутреннего кольца B = 46 мм, угол конуса беговой дорожки в = 11015', диаметр беговой дорожки у упорного бортика dF = 130,6 мм, диаметр упорного бортика d6 = 142,8 мм, ширина упорного бортика а = 7 мм.

Упорный бортик подшипника выполнен в виде сферы, радиус которой по чертежу R₆ 0 = 320 мм. При указанных выше размерах бортика получим S = 0,558° и 0 = 89°27'.Бортик у наружного диаметра имеет фаску А Т = 0,8 мм и выточку у основания высотой А F = 1,5 мм и длиной m = 2,7 мм.Бортик меньшего размера имеет наружный диаметр d б 1 = 121,5 мм.

Подшипник имеет 20 роликов номинальным диаметром D w = 19,55 мм и длиной l w = 35,5 мм. Больший торец ролика выполнен сферическим с радиусом сферы R w 0 = 320 мм. На торце имеется отверстие диаметром d_om = 10,4 мм и глубиной 1 от = 1,5 мм. Меньший торец ролика имеет диаметр D w 1 = 17,387 мм. У торцов роликов имеются радиусные фаски. Величины фасок А = А 1 = 1 мм.

Результаты расчета приведены на рис. 10.

В связи с увеличением центробежной силы роликов усилия в контактах с внутренним кольцом становится меньше, чем с наружным, как видно по графикам.