Распределение напряжений в области контакта абразивного инструмента и обрабатываемого материала

В различных отраслях промышленности значительный интерес представляют звукопоглощающие, демпфирующие, теплозащитные свойства каучуковых покрытий, способных выдерживать многократные знакопеременные деформации, интенсивные вибрационные нагрузки и резкие колебания температур. В тоже время различные ингредиенты, вводимые в состав резиновой смеси перед вулканизацией, приводят к повышению сопротивляемости материала абразивной обработке в процессе формирования поверхности, следствием чего является недопустимый нагрев инструмента в области контакта. Известно, что температуру в зоне абразивной обработки можно снизить уменьшением усилия прижатия инструмента к обрабатываемой поверхности. В тоже время чрезмерное понижение силового воздействия в области контакта приводит к низкому качеству обработки материала. В этих условиях представляет интерес определения взаимосвязи усилия прижатия абразивного инструмента с контактными напряжениями в зоне абразивной обработки. Взаимодействие отдельного зерна абразивного материала и поверхностного слоя покрытия представлено в виде расчетной схемы на рис. 1.

Трофимов Евгений Олегович, заместитель начальника отдела технического контроля.   E-mail:

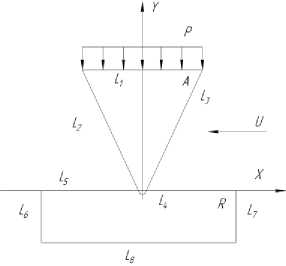
Рис. 1. Расчетная схема взаимодействия зерна абразивного материала и поверхностного слоя

Поверхностный слой покрытия задан прямоугольником, абразивное зерно – треугольником со скругленной вершиной. К верхней кромке зерна приложена прижимающая распределяющая нагрузка p = 1,2 МПа. По оси X заданы горизонтальное перемещение зерна, равное 0,1 мм расстояния. Перемещение основания резинового покрытия по осям Х и Y исключены.

Задача о напряженном состоянии в области контактного взаимодействия решается в плоской постановке в предположении, что оба взаимодействующих тела являются упругими, при этом между упругими телами в процессе контактного взаимодействия при горизонтальном перемещении зерна возникают силы трения, определяемые законом равновесия.

да дт         да дт

— + —xy = 0,  —y ■ — = о дx   ду        ду   дx

Деформация упругих тел может быть выражена через относительные удлинения ε x и

ε y по направлению х, у и через относительный сдвиг γ ху . Величины ε x , ε y , γ ху определяются в свою очередь, через перемещения u и v по направлению осей x и у соответственно:

dud

£ x =    , S y = dx

Y xy

^ 6 u   d v )

~ + — ^5 y   d x )

Дополнительное соотношение между ε x , ε y и γ ху представляет условие совместности:

d4 +dX = 2 52 Y xy dy2   dx2     dxdy(3)

Компоненты деформации связаны с компонентами напряжений следующими соотношениями:

ox = X0 + 2цех oy = X0 + 2цеу

^T xy = ²W xy                         (4)

где θ = ε x + ε y – относительное объемное расширение, а λ и μ – коэффициенты Лямэ, выражающиеся через модуль упругости Е и коэффициент Пуассона v следующим образом:

E v         _ E

( 1 + v )( l - 2 v ) ’     ^{ц 2} ( 1 + v )   ₍₅₎

При постановке контактной задачи напряжениям, деформациям, перемещениям и физическим константам ν, Е присваивается индекс «1» для области А , и индекс «2» для области R. Граничные условия для напряжений на участках взаимодействующих упругих тел, лежащих вне зоны контакта, имеют вид:

^V =- p (x, y )g Li ov = 0  (x, y )g L1, L 2, L4

r ^v = 0 ( x , y ) e L | , L 2 , L 3 , L ₄

CT ² = 0, T 2 V = ⁰   ( ^x, y ) e L 5 , ^L 6 , ^L 7      (6)

где σ v и τ sv – нормальные и касательные н а пряжения на свободных поверхностях, L ₄ и L ₅ – участки соответствующих границ, лежащие вне зоны контакта.

Граничные условия для перемещений были представлены следующим образом:

u 1 = const ( x , y ) e L , L₃

u ² = 0, v ² = 0  ( x , y ) g L_g

где u, v – составляющие вектора перемещений в направлениях x и у соответственно.

При определении граничных условий для напряжений на контактной границе предполагается, что в области контакта происходит скольжение взаимодействующих упругих тел, и соотношение между нормальным и тангенциальным напряжениями подчиняется закону Кулона. Кроме того, нормальное давление, действующее на первое тело вдоль площадки контакта, совпадает с нормальным давлением, которое действует на второе тело. Точно также равны по абсолютной величине и тангенциальные усилия. Обозначив через l линию контакта, представим граничные условия для напряжений на ней следующим образом:

n'v = o2v < 0

I ^T 1 iv |=| ^T 2 iv I ⁽ x , у ) ^g l

I ^T iv | ⁺ P | ^o v | = ⁰

Определение граничных условий для перемещений на контактной поверхности линии l производилось на основе расчетной схемы, представленной на рис. 2.

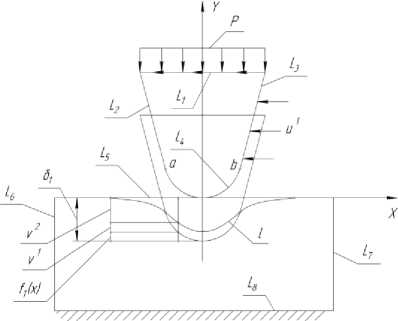
Рис. 2. Схема контактного взаимодействия для определения связи между перемещениями на контактной поверхности

Допустим, что уравнения поверхностей, ограничивающих первое и второе тела до деформации, имеют вид:

f . ( ^x ) =- ( r ² - ^{x 2} ) 1/2 ⁺ r ;   f 2 ( ^x ) = ⁰

Начало координат поместим в точке первоначального касания тел. Под действием прижимного усилия p первое тело (зерно) получит вертикальное перемещение δ1, при этом перемещение второго тела в силу условия закрепления основания равно нулю. Кроме того, произвольная точка предполагаемой поверхности контакта (линия l), расположенная на поверхности первого тела, и вступающая с ней в контакт точка, которая находится на поверхности второго тела, в результате происшедшей упругой деформации получат соответственно перемещения v1 и v2 в направлении у. Так как координаты обеих точек, принадлежащих первому и второму телам, после вступления в контакт становятся одинаковыми, то это позволяет найти следующее условие, связывающее перемещения обоих тел:

V 1 + v 2 = 5 1 — f 1 ( x )

Аналитические методы [2-4] позволяют эффективно решать сравнительно узкий круг контактных задач. При сложной конфигурации взаимодействующих тел и сложных краевых условиях проблема аналитического решения дифференциальных уравнений становится труднопреодолимой. В этом случае широкое применение находят численные методы. В данной работе контактная задача взаимодействия абразивного зерна с резиновым покрытием решалась методом конечных элементов с помощью программновычислительного комплекса ANSYS. В качестве физических констант при решении задачи использовались следующие характеристики: для абразивного инструмента – Е1=35 ГПа, v1=0,3; для резинового покрытия – Е2=50 МПа, v2=0,46. Размер зерна абразивного круга составлял 0,50,63 мм, разрушающее напряжение резинового покрытия было принято равным 4 МПа. На рис. 3 показано распределение первых главных напряжений в поверхностном слое покрытия, контактирующего с абразивным инструментом. Контуром вверху справа показано первоначальное положение абразивного круга. Слева показано его положение после поджатия прижимной силой и перемещения влево. На данном рисунке показано, что существует область, где главные напряжения, соответствующие напряжениям растяжения, достигают значений, превышающих предел прочности материала при растяжении, составляющих 4 МПа, что свидетельствует о начале обработки покрытия.

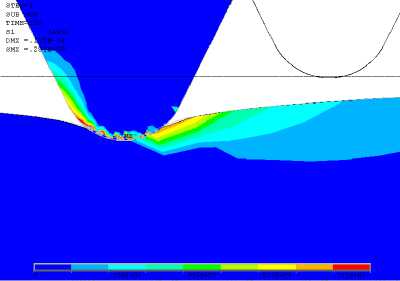
Рис. 3. Распределение первых главных напряжений в зоне контакта при абразивной обработке

Выводы: разработанный метод расчета позволяет определить напряженное состояние в зоне абразивной обработки резинового покрытия в зависимости от усилия прижатия абразивного инструмента. Он может быть использован для разработки практических рекомендаций по оптимизации технологических параметров обработки.