Распределение напряжений в поперечных сечениях контейнеров из стеклопластика и полимербетона, используемых для длительного хранения высокоагрессивных сред

Кутергин Алексей Владимирович, магистрант Фукалов Антон Александрович, аспирант представительных объемов матрицы, наполненной минеральной мукой, и пространственной гексагональной ячейки периодичности полимербетона, содержащей армирующие минеральные частицы в наполненной матрице.

Определение эффективных упругих модулей квазиизотропной матрицы на основе полиэфирной смолы Виналкид 550 (модуль Юнга и коэффициент Пуассона – Е =5,3 ГПа и υ=0,25), наполненной мраморной мукой (модули Юнга в плоскости изотропии и в нормальном ей направлении Е =55,0 ГПа и E = 23,0 ГПа и коэффициенты Пуассона и=0,29 и и = 0,32 ) до концентрации 26%, проводилось на основе численного решения краевых задач в конечно-элементном пакете ANSYS 12.0 для независимых реализаций представительных объемов, характерные размеры которых определялись при помощи метода, предложенного авторами [1-4], а сами пространственные случайные структуры были сгенерированы при помощи алгоритмов [5-8]. Полученные результаты показали, что наполненная матрица статистически изотропна, имеет эффективный модуль Юнга Е =8,276 ГПа и коэффициент Пуассона υ=0,24, которые попадают в ограничения Фойгта-Рейса и находятся вблизи нижней границы оценки Хашина-Штрихмана. Для проверки этих результатов были также спрогнозированы свойства полимербетонов аналитически в рамках полидисперсных моделей механики композитов [9, 10]. Отклонение численных значений эффективного модуля объемного сжатия матрицы, наполненной мраморной мукой, от аналитической оценки не превышает 5%.

Вычислительные эксперименты в пакете ANSYS 12.0 позволили также определить эффективные упругие модули полимербетона (модули Юнга и коэффициенты Пуассона в плоскости изотропии Е=29,20 ГПа, и=0,19 и в нормальном к ней направлении E — 27,30 ГПа и V — 0,21), матрица которого - полиэфирная смола Виналкид 550, наполненная мраморной мукой, а армирующая фаза - сферические трансверсально-изотропные частицы диабаза, образующие пространственную гексагональную структуру с объемной долей минеральных включений 60%.

Контейнеры для хранения высокоагрессивных веществ являются тяжелыми составными цилиндрами, изготовленными из анизотропных материалов. Составные части этих конструкций ограничены цилиндрическими поверхностями радиусов а и b ( a < b ), а поверхность контакта находится на расстоянии c от оси симметрии. Будем считать, что материал обоих цилиндров линейно-упругий однородный, с постоянной плотностью по всему объему, обладает цилиндрической ортотропией. Наиболее распространенными видами нагрузки являются статическое или изменяющееся во времени внешнее и/или внутреннее давление и собственный вес. В простейшем случае, пренебрегая влиянием торцевых нагрузок, контейнер может быть представлен в виде бесконечного составного горизонтального ортотропного цилиндра, жестко закрепленного по внешней поверхности и находящегося в равновесии под действием массовых сил.

В силу бесконечной протяженности цилиндра функции перемещений, деформаций и напряжений не зависят от осевой координаты z , цилиндрической ортогональной системы координат r ,9 и z, вследствие чего уравнения равновесия могут быть записаны в следующем виде:

⁽ k ' 5т⁽ k ' п⁽ k '   п⁽ k '

d°rr + 1 dTre , °rr   °ee _ (k'

+      +            p cos v dr    r de        r                ,(1)

i     (k'    a (k'

1 'г'66 %- e + 2 %e_ = —p( k' sin e r de     drr

.

Здесь p ^{( k} ) - удельный вес материла. Все константы и функции будем обозначать верхними индексами 1 и 2 для внутреннего и вешнего цилиндров соответственно. Определяющие соотношения

_п ^{( k} ' _ j k ' ^k '_F( ^k ' ₊ И ^k Н ^k ' ° rr = K ii ^ь rr ⁺ K 12 ^b ee

„( k ) _ ^( k Ы k ) , ^( k L( k )

° ee = K 12 ^b rr ⁺ K 22 ^b ee

(k >CT< k'    H(kk

( k )    p ( k ) ^p rz ° rr    ^p z e P qQ

° zz   Ez I   H k'  + k Er        Ee

• -^{( k} ' _ Д ^k Ц ^k '

• T re — Gre Y re ,(2)

для тяжелого составного ортотропного осесимметричного тела, находящегося в условиях плоской деформации, содержат коэффициенты

• ( k )

^{( k} )     ^Er          ..( ^{k )}..^{( k} )\

K 11 ^—   ( k )^{( 1 p}e z ^H z e '

,

K k ' —^ ( H r S ' +H ri H k l

• ( k )                              ,

к ( k ) ₌ E e-fi-uC k )_u( k )\

K 22     ^( k ) ^{( 1 H} rz ^H zr '

D ( ^k ' -1 - 2u( ^k 'u( ^k 'u( ^k ' - ц( ^k 'u( ^k ' - u( ^k M ^k ' -   ^k )ц( ^k '

^D = ^{1   2 p} r e ^p e z ^H zr   ^H r e ^p e r   ^p e z ^H z e    ^H zr ^p rz

, определяемые модулями Юнга Er(k), E9(k) и Ez(k) в направлениях r,9 и z, коэффициентами Пуассона (k)       (k)          (k)

^H r e , P_e z и P zr ' , поперечным модулем сдвига G ^{( k} '

Gr e .

Последовательная подстановка геометрических соотношений Коши

( k ^du ^ k^   ( k ) ₌ u ( k ⁾ 1 5 v ^{( k} '

e rr             bee dr          r r de

,,

( k ) _ 1 д u ^{( k} ' d v ^{( k} ' v ^{( k} '

• Y^V ■ e = дд- ⁺

r de     d r     r                (3)

в определяющие (2), а затем полученного результата в уравнения равновесия (1) позволяет записать неоднородную систему дифференциальных уравнений Ламе в частных производных, которые не приводятся ввиду громоздкости. Граничные условия на жестко закрепленной внешней ( r = b ), свободной от нагрузок внутренней ( r = a ) и контактной ( r = c ) поверхностях

u(2'|     = v(2'|     = 0 °(1)|

Ir=b        lr=b          rr r=a т (1)l

^T r ⁶ r = a " 0 ^,

(I (1'1     -M(2)| uu

I r — cr

, a «I/.

rrrr

Ir—cl v (1'|     — v (2'|

I r—c          L т (1'1 -t(2)I

^T r e     ^{— T} r e

I r — c            I.

,

не нарушают симметрию задачи, что позволяет применить метод, основанный на разложении компонент вектора перемещений по окружной и радиальной координате в тригонометрические и обобщенные степенные ряды [11-14]. Разложение по окружной координате в тригонометрические ряды

U  — и 0 + u 1 ^cos e+ £ ”2 и ^{( k} ' cos i e

, v(k' — v(k 'cos e + £” 2vz(k 'sin i e позволяет понизить размерность задачи и перейти к последовательности систем обыкновенных дифференциальных уравнений, однородных при i^1. Вид граничных условий (3) позволяет сделать вывод о том, что все системы при i^1 имеют единственное тривиальное решение: ui(k)=0 и v,(k)=0, а совместное использование метода вариации произвольных постоянных и разложения вектора перемещений по радиальной координате в обобщенные степенные ряды позволяют получить точное аналитическое решение задачи о равновесии

толстостенного тяжелого составного ортотропного цилиндра с жестко закрепленной внешней поверхностью [13]

_M ⁽ k       ^k )_rP k ₊ (k ^k L-P k ₊ (k ^k )l_nr + a^{( k} ) + S^{( k} X2 ²VosO

U1 — \ ai r + a2 r + a3 ^n r + a4 +     ' I cos

, v(k) -UkVkVk + AkWkV-₽k - akk^r-a^k) + 4(kA2'I sin 6 v — । a^ a| r + ^2 a^ r      a^ ^n ' a4  + ^ r ) s^n

Здесь

a^{( k} ) —

pk (kk + 1)+ pk +1

e 2 - p k

-

,

a⁽ k )- a 2 —

-

P k ( k k + 1 ) - P k ² — 1

P k ^{- p}k

-

,

n k ^{+ P k -} q k ( ^{2 + k}k ) ^{+ 1}

A ^k ) —

( « V N ^k ) - 1 ) p^{( k} )

,

0 ^{( k} ) —

to ( ^k ) — 4

—

to ( k )fi( k ) ® 3 G r 6

co^{( k)}G⁽-^k ) ^ю 3 G r 6

,

_B ( k ) _ 0^{( k} ) p ^{( k} )

^{B —}   G rk )

К ^{( k} ) fm^{( k} )ю^{( k} ) w 11   « 1 « 3

+® r 6 ⁾ K )

+ to (k XA k )) + ^2 ^4

,

m k ^- n k

« 3 ^k ) — 3

—

,

® 2 ^k ) ^{— 2} q k ⁺ m k

—

p k to 4 ^k ) — 2 k ^ + p k + 3

,

,

,

n k ²

,

mk —

G ^{( k} ) Gr 6

1 K «•

n k ^—

к ^{( k} )

K ₂₂

,

4 K ^{( k 1}   q ^{k —}

P k ^—

к ^{( k} )

K ₂₂

. g Y ,

^kk ^—

к ^{( k} )

K 21

V G r o¹

•

Постоянные интегрирования a / ^k\ a ^-^k ) , a ₃ ^{( k} ) и a ₄ ^{( k )} , входящие в общее решение (5) неоднородной системы обыкновенных дифференциальных уравнений при i =1 определяются первым членом разложения граничных условий (3) в тригонометрический ряд по окружной координате и не приводятся ввиду громоздкости. Подстановка уравнений (5) последовательно в геометрические (4) и определяющие (2) соотношения позволяет записать выражения для напряжений. Обратим внимание на то, что в частном случае для изотропного тяжелого горизонтального составного цилиндра новое решение совпадает с результатами, приведенным в работе [11], а в случае, когда можно пренебречь вкладом массовых сил - совпадает с решением [15].

Поскольку полимербетон и стеклопластик имеют ярко выраженную анизотропию свойств, то прочностной анализ элементов конструкций, изготовленных из таких материалов, необходимо осуществлять на основе многокритериального подхода [16]. Инвариантными относительно ортогональных преобразований, допустимых над цилиндрически ортотропным однородным телом, являются компоненты тензора напряжений в главных осях, которые позволяют описать различные механизмы разрушения от растяжения или сжатия в окружном,

осевом и радиальном направлении, от сдвигов в поперечных плоскостях.

Будем рассматривать контейнер, представляющий собой жестко закрепленное по внешней поверхности цилиндр с геометрическими параметрами: a =0,3 м, c =0,5 м и b =0,6 м, состоящий из внутренней полимербетонной ( E r ⁽¹⁾ = E ₆ ⁽¹⁾ =29,2 ГПа, E z ⁽¹⁾=27,3 ГПа, G^ ⁽¹⁾ =11,5 ГПа, ц Г П — 0,19 , ц⁽ 1 ) — 0,21 и y⁽¹⁾=25 кН/м ³ ) и внешней стеклопластиковой ( E r ⁽²⁾ =11,8 ГПа, E ₆ ⁽²⁾ =56,8 ГПа, E_z ⁽²⁾ =15,7 ГПа, Gn ⁽²⁾ =9,8 ГПа, ц б ²? — 0,06 , M⁽ _r 2 ) — °,38, p⁽ _z e — 0,21 и у ⁽²⁾ =19 кН/м ³ ) составных частей. На рис. 1 и 2 представлены распределения ненулевых компонент тензора напряжений в поперечных сечениях контейнеров, вызванные массовыми силами и внутренним давлением р =0,4 МПа, вдоль меридиональной и обезразмеренной радиальной p — ( r - P l )/( p ₂ - Р 1 ) координаты.

Вклад массовых сил в распределение напряжений для конструкции контейнера заданной геометрии не превышает 5%. Касательные напряжения, возникающие в поперечных сечениях, определяются исключительно массовыми силами, в результате чего их величина не зависит от заданного равномерного давления (рис. 1). Радиальные напряжения по абсолютной величине убывают от нагруженной давлением внутренней к закрепленной внешней поверхности. Окружные и осевые напряжения имеют скачок на поверхности контакта.

В процессе формования элементов конструкций из стеклопластика существует ряд факторов, которые приводят к возникновению собственных технологических напряжений: различие в геометрии отдельных частей, приводящее к натягу, технологическое натяжение волокон (обязательное условие при формовании волокнистого материала), которое после намотки нескольких слоев стеклопластикового цилиндра проявляется в виде давления по поверхности контакта [17]; усадка связующего при отверждении и др. Определение закона распределения собственных технологических напряжений в поперечных сечениях является самостоятельной задачей, которая выходит за рамки данного исследования. Однако для оценки начальной прочности контейнера с учетом этого фактора будем предполагать, что технологические напряжения известны, имеют единственную, отличную от нуля, радиальную составляющую (контактное давление р_С ) и равномерно распределены только по поверхности сопряжения внутреннего и внешнего цилиндров.

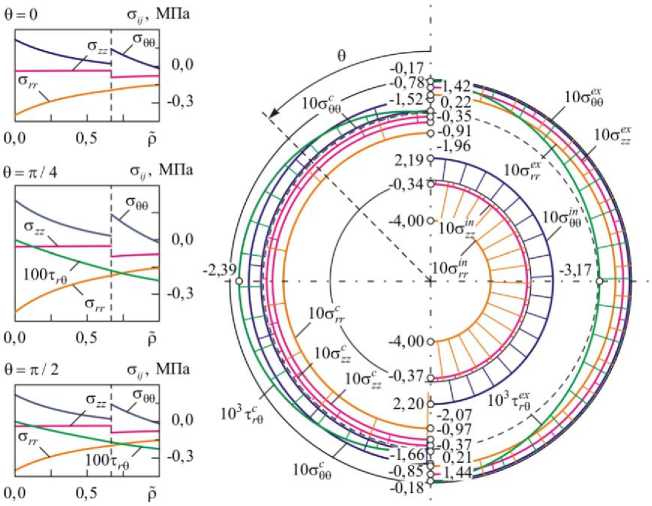
Рис. 1. Распределение напряжений (МПа) на нагруженной давлением р =0,4 МПа внутренней ст ” , закрепленной внешней ст j и контактной ст c поверхности контейнера

Наибольший вклад в распределение напряжений в поперечных сечениях контейнера, вызванных сочетанием нескольких факторов, вносит контактное давление рС =1,96 МПа (рис. 2). Наибольшие по абсолютной величине значения радиальных, окружных и осевых напряжений достигаются на верхнем и нижнем сводах цилиндрического контейнера и, следовательно, эти точки являются наиболее опасными с точки зрения возможности начала разрушения, от растяжения или сжатия в соответствующем направлении. В свою очередь, максимумы касательных напряжений лежат в горизонтальной диаметральной плоскости, что с точки зрения оценки начальной прочности свидетельствует о возможности начала разрушения контейнера по механизму сдвига в диаметральной плоскости.

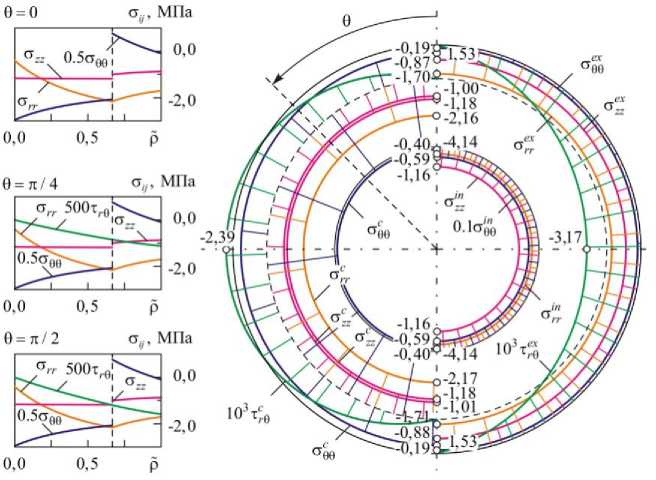
Рис. 2. Распределение напряжений (МПа) на нагруженной давлением р =0,4 МПа внутренней ст n , закрепленной внешней ст ex и контактной ст c поверхности контейнера, с учетом контактного давления

Выводы: несмотря на то, что вклад массовых сил в напряженное состояние контейнера из стеклопластика и полимербетона не превышает

5%, полученное аналитическое решение позволяет учесть еще и неоднородные реакции основания [14], а также любые другие нагрузки, симметричные относительно вертикальной диаметральной плос-  9.

кости, которые можно разложить в тригонометрические ряды.