Распределение плотности температурных коэффициентов для мюонов в атмосфере

При использовании данных мюонных телескопов в анализе вариаций космических лучей следует учитывать вклад атмосферных эффектов, в основном барометрического и температурного. Если барометрический эффект интенсивности мюонов оценивается достаточно просто, поскольку определяется одним параметром — давлением на уровне наблюдения, то с температурным эффектом все не так однозначно. Температурный эффект мюонов определяется несколькими параметрами, характеризующими состояние атмосферы от слоя генерации до уровня регистрации мюонов. Эмпирический метод определения температурного эффекта [Duperier, 1949] предполагает обычно использование двух параметров (например, высоты и температуры слоя генерации мюонов), которые находятся из корреляции с наблюдаемой интенсивностью. Данный метод отличается простотой и свободен от возможных ошибок теоретических расчетов коэффициентов. Однако эмпирический метод не учитывает распределение масс, полностью и однозначно контролируемое температурным разрезом от уровня наблюдения до границы атмосферы. Интегральный метод учета температурного эффекта [Дорман, 1957] предусматри- вает использование полного температурного разреза атмосферы и свободен от указанных недостатков. Для реализации интегрального метода необходимы регулярные данные аэрологического зондирования и распределение плотности температурных коэффициентов для мюонов в атмосфере. Цель данной работы — найти функцию распределения плотности температурных коэффициентов W(h) для мюонного телескопа станции космических лучей «Новосибирск» и подземного комплекса мюонных детекторов в Якутске, расположенных на глубине 0, 7, 20 и 40 м водного эквивалента (в. э.).

РАСЧЕТ РАСПРЕДЕЛЕНИЯ ПЛОТНОСТИ ТЕМПЕРАТУРНЫХ КОЭФФИЦИЕНТОВ

ДЛЯ МЮОНОВ В АТМОСФЕРЕ

Функция W(h), имеющая значение плотности температурного коэффициента (ПТК), впервые была введена в 1956 г. [Дорман, Фейнберг, 1956]. Теоретические расчеты функции W(h) выполнялись для различных условий регистрации мюонов [Дорман, 1957; Кузьмин, 1964; Дорман, Янке, 1971; Дмитриева и др., 2009; Berkova et al., 2008; Волкова, 2013]. Методы расчета W(h) в этих работах различаются незначительно и в основе их лежат представления работы [Дорман, 1957]. Однако результаты этих работ не имеют полного согласия, поскольку расчеты проводились при различных значениях исходных параметров. На основании результатов работ [Дорман, 1957; Дорман, Янке, 1971] направленную интенсивность мюонов представим выражением

Nи (As, ho,9) = h 0    h2     »     V                                  (1)

= J dh 2 J dh i J d ^ J d ^sn F ( ^,^, h i , ^h 2 , ^h o ,9 ) ,

^{0        0       S}MUH       ^s _n +

h 0       ^h 2        »        ^sn ^-

^- J dh 2 J dh i J d ^ J d Е _я F ^(sn^,sn , h i , h 2 , h о^{,9) x}

^{0       0      s}мнн      ^sn ⁺

x — b ⁿ— J dh 5 T ( h ) - ε cosθ h

h 0        h 2         да         s n -

^- J ^dh 2 J dh i J d ^ J d^F ^(sn^,sn , h i , ^h 2 , ^h о^,9) Ь ^ ^{x (3)}

^{0       0}       = мнн      ^sn ⁺

h ₀

x J

δ T ( h ) dh h [s _g cos9 - а _и ( h - h ₂ )],

где

F ( ^sn^,sn , h 0 , h i , h 2^,9 ) =

m n c f - ^{( S}n , h i , ⁹ ) _x

τ ε cosθ ππ

x

⁽ ’

- ^Sn + ) P ⁽ h 2 )

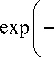
h ₂ - h ₁

l _π cosθ

x exp

I

m n c    h ^{2 dh}

^Tn^sn cos ^{9 J} P ( ^h )_?

m cR      mμcR где Ьп =-----, Ь =-----. Исходя из (3), относи-

τπg     μ    τμg тельное изменение интенсивности мюонов, обусловленное температурным эффектом, можно записать в следующем виде:

^{5 N} ( ^{A s} i h o₁⁹ ) = Г w ( A s, h , 9)5 т ( h ) dh .          (4)

N ( A s, h 0 ,9)    ^{J Tl}      0’

Функция плотности температурного коэффициента

W_T ( A s, h , h 0 ,9) = W T ( A s, h , h 0 ,9) + W T ( A s, h , h 0 ,9) (5)

m и c J___________ dh___________

\ I P ( h Ж cos ^{9 - а}и ( h ^- h 2 ) ],

включает температурный эффект мюонов

W T ( A s, h , h 0 ,9) =

Здесь s + » s_u, π ^μ

sn          aи (hо - h2)+ As s = —. s = —----------- , мин

^π    α ²              αcosθ

^^^^^^B

i h0       h2        CO dh dh   dε

^N μ 00ε мин

μ

; и x

минимальная энергия пионов, мюоны от которых могут регистрироваться данным детектором, As — минимальная энергия мюонов, регистрируемых данным детектором, s^ — полная энергия мюона, h — глубина атмосферы, h ₀ — уровень наблюдения, h ₁ — уровень генерации пионов, h 2 — уровень генерации мюонов, 9 — зенитный угол прихода частиц, m _п и m _и — массы покоя пиона и мюона, т _п и т _и — времена жизни пиона и мюона в покое соответственно, р ( h )= gh / RT ( h ) — удельный вес воздуха на высоте с давлением h , g — ускорение силы тяжести, R — удельная газовая постоянная, T ( h ) — температура воздуха в кельвинах на высоте с давлением h , c — скорость света, а= m _и / m _п , а _и — потеря энергии частицы на ионизацию, l _п — пробег пионов до ядер-

A f h )

ного захвата, f,(Sn,hi,9) = — expl - r 1 л I — sn ^ L cos 9 J дифференциальный спектр пионов, A — постоянная, L — средний пробег поглощения для нуклонной компоненты, у — показатель дифференциального спектра пионов. Изменения интенсивности мюонов при вариации распределения температуры (температурный эффект) находятся в результате варьирования выражения (1) по соответствующей независимой переменной:

sn - x J dsn sn +

b _μ F (ε _π ,ε _μ , h ₁ , h ₂ , h ₀ ,θ)

h [s _и cos 9 - а _и ( h - h ₂ )] ’

обусловленный распадом и ионизационными потерями мюонов в атмосфере (мюонный эффект), и температурный эффект пионов

WT (As, h, h0,9) = h o       sn-

= — J dh i J d S и J ds n       F (S п ,S и , h i ,h 2 , h о ,9) - (7)

N и 0     s_-1H     s n +       T ^{( h} )

1 h        ^h 2        CO        ^sn -

^- —J dh 2 J dh i J d ^ J d S n

N и 0      0     s,„     s n +

b _π F (ε _π ,ε _μ , h ₁ , h , h ₀ ,θ)

h ε cosθ

,

обусловленный распадом и захватом пионов (пион-ный эффект).

5 N /As, h о ,9) =

= J dh 2 J dh i J d s _g J d s n F (s^, h i ,h 2 , h о ,9) -

^{0       0      s}мнн      ^sn ⁺

РЕЗУЛЬТАТЫ РАСЧЕТА

Расчет W ( h ) выполнен для направления прихода частиц с зенитного угла 9=0° и для значения у =2.5 (рис. 1). На рис. 1 приведены для сопоставления результаты, полученные ранее другими авторами (также для 9=0° и у =2.5-2.8), а ниже, в табл. i, — значения исходных параметров, использованные в расчетах.

С целью сопоставления результатов расчетов данной работы с результатами [Дорман, Янке, 1971] нами были выбраны близкие значения исходных параметров (см. табл. 1). Несмотря на это, небольшие расхождения (рис. 1) имеют место. Они возникают по следующим причинам. В [Дорман, Янке, 1971] используется ряд приближений при интегрировании по h 1 и s _мин , а именно: применяется теорема

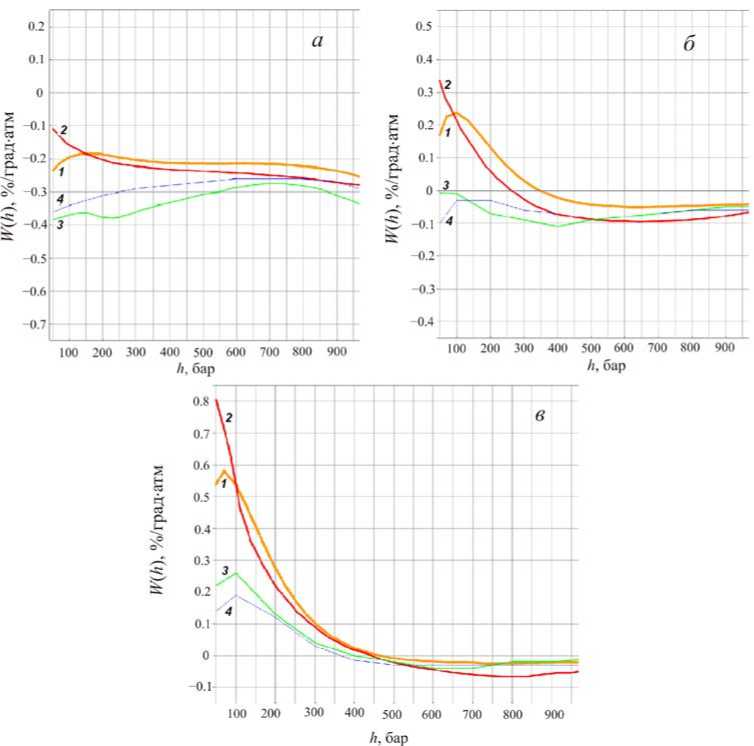
Рис. 1. Распределения плотности температурных коэффициентов интенсивности мюонов в атмосфере, полученные разными авторами (1 — данная работа, 2 — [Дорман, Янке, 1971] , 3 — [Кузьмин, 1964] , 4 — [Дмитриева и др., 2009] ) при различных значениях минимальной энергии регистрируемых мюонов As : а — As =0.24-0.5 ГэВ; б — As =2.2-6.4 ГэВ; в — ∆ε =10.0–16.2 ГэВ

Таблица 1

Значения исходных параметров, используемые в расчетах

Автор Рис. 1, а Рис. 1, б Рис. 1, в ∆ε, ГэВ γ l, г/см2 L, г/см2 ∆ε, ГэВ γ l, г/см2 L, г/см2 ∆ε, ГэВ γ l, г/см2 L, г/см2 1 0.4 2.5 60 120 6.4 2.5 60 120 14.4 2.5 60 120 2 0.4 2.5 60 120 6.4 2.5 60 120 14.4 2.5 60 120 3 0.24 2.8 75 75 4.5 2.8 75 75 16.2 2.8 75 75 4 0.5 2.7 120 110 2.2 2.7 120 110 10.0 2.7 120 110 о среднем для промежуточных интегралов с учетом медленно меняющихся подынтегральных функций, используются оценочные выражения, интегралы вычисляются методом последовательного приближения, в то время как в настоящей работе производится прямой расчет. Имеются различия и в высотных профилях температуры атмосферы для Москвы и Новосибирска. Следует заключить, что результаты, представленные на рис. 1, трудно сопоставимы (за исключением результатов данной работы и работы [Дорман, Янке, 1971]). Расхождение в первую очередь объясняется ощутимыми различиями значений исходных параметров, используемых в расчетах (табл. 1). В данной работе используется модель стандартной атмосферы, потери мюонов считаются постоянными, рассматривается только вклад пионов, поскольку установка в Новосибирске регистрирует мюоны до 200 ГэВ (иные каналы рождения мюонов включаются только после 104 ГэВ [Кочанов, 2008]).

ЗАВИСИМОСТЬ

РАСПРЕДЕЛЕНИЯ W ( h )

ОТ ПРОБЕГОВ ПОГЛОЩЕНИЯ ПРОТОНОВ И ПИОНОВ

В АТМОСФЕРЕ

Рассмотренные выше результаты получены при пробегах поглощения протонов от 75 г/см2 [Кузьмин, 1964] до 120 г/см2 [Дорман, Янке, 1971] и пробегах поглощения пионов от 60 г/см2 [Дорман, Янке, 1971] до 120 г/см2 [Дмитриева и др., 2009]. При этом показатель спектра γ принимался у разных авторов равным 2.5; 2.7; 2.8. В дальнейшем при расчетах, учитывая последние данные [Мурзин, 2007; Карелин и др., 2011], γ примем равным 2.75 [Карелин и др., 2011]. Расчет W(h) для различных значений пробегов поглощения протонов и пионов выполнен для вертикальной интенсивности мюонов на уровне моря (θ=0) при ∆ε=0.6 ГэВ. Полученные таким образом результаты расчетов представлены на рис. 2.

Наблюдается (см. рис. 2) заметная зависимость распределения W ( h ) от величины пробегов поглощения, особенно от пробега поглощения первичных протонов в атмосфере (рис. 2, а ).

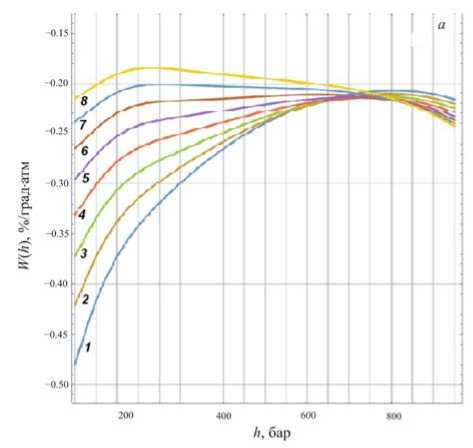
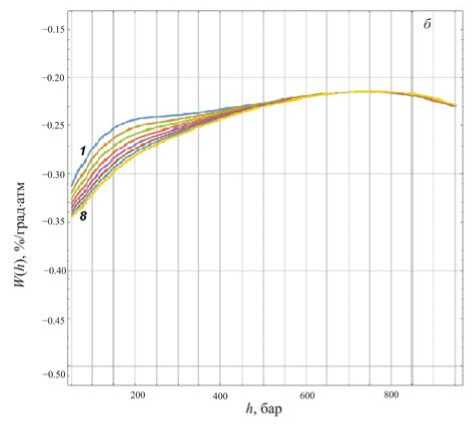
Рис. 2. Распределения W ( h ) при постоянных значениях пробега поглощения пионов l =110 г/см² ( а ) при значениях пробегов поглощения протонов L от 80 до 150 г/см² (кривые 1–8 соответственно); а также пробега поглощения протонов L =110 г/см² ( б ) при значениях пробегов поглощения пионов l от 80 до 150 г/см² (кривые 1–8 соответственно)

РАСПРЕДЕЛЕНИЯ W ( h ) ДЛЯ ИНТЕНСИВНОСТИ МЮОНОВ, РЕГИСТРИРУЕМЫХ

ПОД РАЗЛИЧНЫМИ УГЛАМИ К ЗЕНИТУ

Расчет проводился для различных значений зенитных углов θ телескопа, каждому из которых соответствует эффективный порог ∆ε регистрации мюонов (табл. 2).

Таблица 2

Параметры мюонного телескопа в Новосибирске

θ, °	0	30	40	50	60	67	71
∆ε , ГэВ	0.6	0.69	0.78	0.93	1.2	1.5	1.8

Во всех расчетах принимается стандартная атмосфера, распределение температуры Т ( h ) для которой представлено на рис. 3.

Пробег поглощения протонов в области энергий 5–200 ГэВ, согласно [Мурзин, Сарычева, 1968; Хаякава, 1973; Мурзин, 2007; Сарычева, 2007] , примем равным 110 г/см². Расчет выполнен для различных значений пробегов поглощения пионов l от 70 до 110 г/см². Результаты расчета представлены на рис. 4 для различных зенитных углов регистрации мюонов.

Более значительные изменения в распределении W ( h ) в зависимости от l наблюдаются с ростом зенитного угла θ регистрации мюонов.

РАСПРЕДЕЛЕНИЯ W ( h )

ДЛЯ МЮОНОВ, РЕГИСТРИРУЕМЫХ

ПОД ЗЕМЛЕЙ

Расчет выполнен для зенитных углов регистрации мюонов 0, 30 и 60° на глубине 0, 7, 20 и 40 м в.э. Использовались следующие значения исходных параметров: γ =2.75; L =110 г/см²; l =120 г/см². При этом ∆ε принимает следующие значения: 0.24 ГэВ (уровень моря); 1.6, 1.85, 3.2 ГэВ (7 м в. э.); 4.5, 5.2, 9.0 ГэВ (20 м в.э); 9.5, 10.97, 19.0 ГэВ (40 м в.э.). Результаты представлены на рис. 5.

Результаты расчета плотности температурных коэффициентов для мюонов в атмосфере, регистрируемых установками в Новосибирске и Якутске, в цифровом виде представлены в табл. 3–8 (см. приложение).

ЗАКЛЮЧЕНИЕ

Путем расчетов найдены распределения плотности температурных коэффициентов интенсивности мюонов в атмосфере W ( h ) для различных зенитных углов регистрации на уровне моря и на различных глубинах под землей. Следует отметить наблюдаемую зависимость функции W ( h ) от пробегов поглощения протонов и пионов в атмосфере, особенно от их соотношения ( L ≤ l или L ≥ l ). И если пробег поглощения протонов в верхних слоях атмосферы известен, то о пробеге поглощения пионов этого, к сожалению, сказать нельзя.

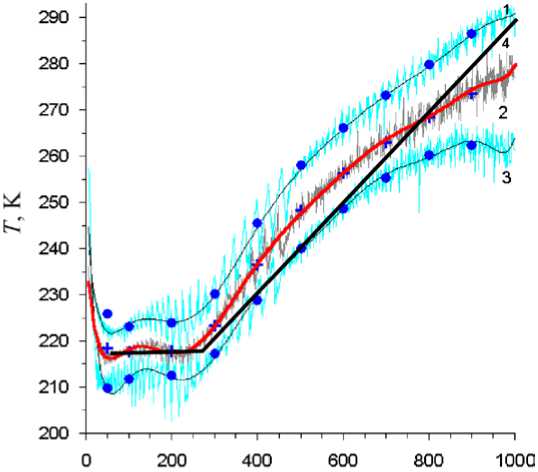
А, мбар

Рис. 3. Высотный ход температуры атмосферы над Новосибирском: 1 — лето, 2 — весна и осень, 3 — зима, 4 — кусочно-линейная функция аппроксимации

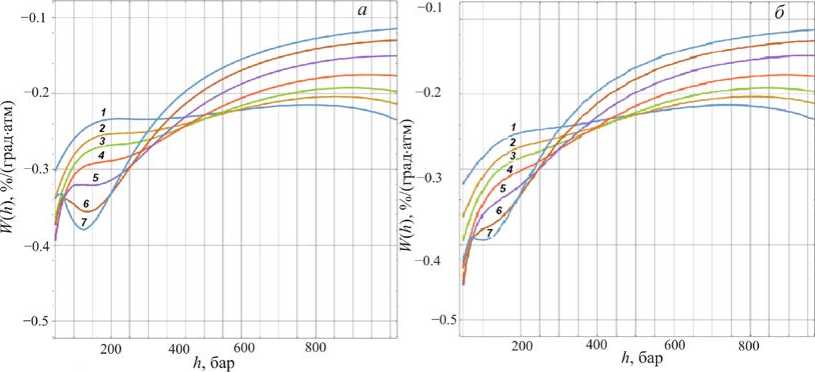
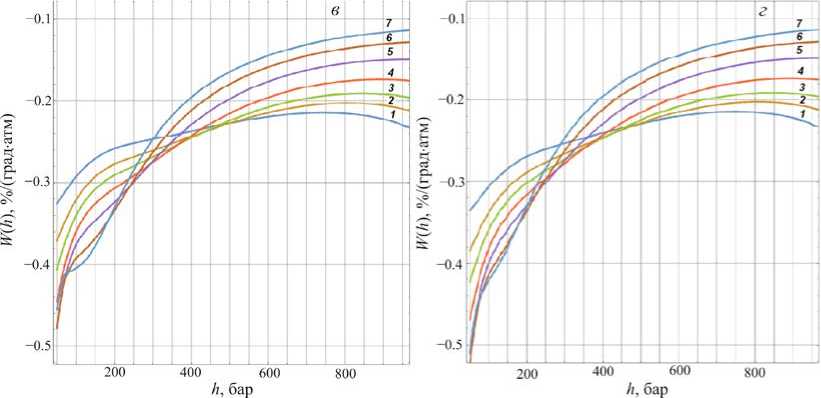
Рис. 4. Распределения W ( h ) для зенитных углов регистрации мюонов от 0 до 71° (кривые 1-7 соответственно) при значениях пробега поглощения пионов 70 ( а ), 90 ( б ), 100 ( в ), 110 г/см² ( г )

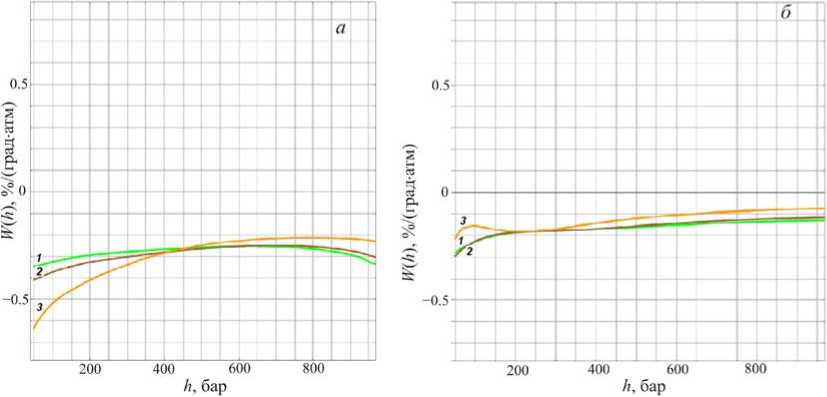
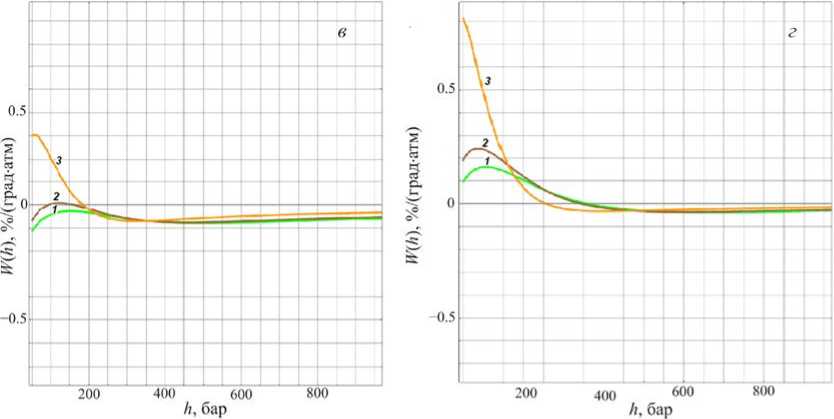
Рис. 5. Распределения W ( h ) для мюонов, регистрируемых на уровне моря ( а ) и под землей на глубине 7 ( б ), 20 ( в ) и 40 м в.э. ( г ) под зенитными углами 0, 30 и 60° (кривые 1–3 соответственно)

Сравнение показывает, что распределения W ( h ), полученные в разных работах, трудно сопоставимы (за исключением результатов данной работы и работы [Дорман, Янке, 1971] ). Расхождение результатов в первую очередь объясняется ощутимыми различиями значений исходных параметров, используемых авторами в расчетах.