Распределение полей давления и деформаций, возникающих при ударе твёрдого тела о деформируемую преграду

случае, естественно, для преграды задаются параметры, характерные для биологического тела.

Нами использовался численный метод расчета упругопластических течений, основанный на решении конечно-разностных уравнений [1]. Этот метод достаточно широко применяется в работах по гидродинамике, а также при исследовании пластичности металлов [2]. При выборе этого метода применительно к нашей задаче мы исходили из предположения, что он может открыть новые возможности для расчета деформаций в биологических структурах, в том числе – с учетом нелинейности их материала.

Кратко суть метода состоит в расчете скоростей и перемещений узлов расчетных сеток, конфигурация которых выбирается исходя из требуемого соотношения точности и сложности моделирования. В нашем случае с необходимостью расчет проводится с использованием подвижных сеток, поскольку имеет место перемещение границ рассматриваемой сплошной среды. Поэтому задача решается в переменных Лагранжа, т.е. рассматривается перемещение подвижных сеток [3].

ВЕСТНИК 2014. ВЫПУСК 4

Отметим, однако, что применение так назы- ваемых лагранжевых сеток ограничено кругом задач с относительно небольшими деформациями среды, следовательно, они не подходят для ситуаций с пробитием мягких тканей. Тем не ме- нее, с их помощью можно получать косвенные данные об уровне возникающих в этом случае нагрузок и тем самым косвенно судить о характере протекания процесса.

Для расчета упругопластических течений необходимо задать уравнение состояния. Уравнение состояния должно описывать упругую, упругопластическую и гидродинамическую стадии движения. Для последних двух режимов движения должны быть сформулированы соответствующие критерии текучести.

ВЕСТНИК 2014. ВЫПУСК 4

Основные уравнения

1. Уравнения движения: d Z    a t.

x-^^ + ^^ _ Р x, дx    дy (1) д T  дУ —- +---yy- _ py, дx дx (2) где Txy – касательное напряжение; полные напря-

– p - плотность, Z , Z xx yy жения;

Z xx = s. - ( P + q ) . Z „ = S„ - ( P + q ) • (3)

где q

–

искусственная вязкость (вводится для расчета гидродинамических ударных волн, позволяя заменить скачок давления в ударной волне его быстрым, но непрерывным изменением), S и P – соответственно девиаторная и гидростатическая составляющие напряжений:

P представляет собой среднее арифметическое трех напряжений сжатия, т.е.:

• -P = 3(а1 + а2 + аз ) • (4)

• 2.    Уравнение неразрывности (выражает в дифференциальной форме закон сохранения массы для любого объёма движущейся жидкости): •

  V _ д 5с д y

  V д x д у ’

  
  

• 3.    Уравнение энергии (выражает закон сохранения энергии в дифференциальной форме):

Здесь и ниже используются принятые обозначения, согласно которым напряжения положительны при растяжении и отрицательны при сжатии, а знак их противоположен давлению. Поэтому перед давлением появляется знак минус.

При описании текучести и пластического течения ограничиваются лишь теми компонентами напряжений, которыми обусловлена деформация сдвига. Поэтому каждое напряжение ст 1 , а ₂, а ₃ раскладывается на гидростатическую составляющую P и девиатор-ную часть S , то есть будем иметь соотношения: а 1 = - P + S 1 ; а ₂ = - P + S ₂; а ₃ = - P + S 3 .

где V – относительный объём.

E _-(P + q ) V + V (SxxE xx + SyyE yy + Tx-Exy ), (6)

где E – внутренняя энергия на единицу началь^ного объема, E xx , £ yy , £ _X y ^- деформации ^s xx , S_yy – компоненты девиатора напряжений. Искусственная вязкость (квадратичная) необходима, чтобы создавать сопротивление между движущимися слоями текучих тел (не твердых):

q _ C o2 p ⁰ ( V / V ) 2 A / V,           (7)

где C ₀ – постоянная, A – площадь ячейки.

Использование квадратичной вязкости по- зволяет локализовать разрыв давления и скорости на ударном фронте на ограниченном числе ячеек, причем это число остается постоянным по мере прохождения волны давления через сетку.

• 4.    Уравнения состояния (служат для связи напряжений и деформаций):

• • Компоненты напряжений:

S. _ 2^Exx - - V / V 1 + ^x,(8)

xx            xxxx

Syy _ 2^l Eyy - - V / VI + Syy ,(9)

Ty _ ЦЕxy + Sxy ,(10)

где ц - модуль сдвига, 5 - поправки на поворот, которые прибавляются к напряжениям.

При смещении элемента среды из начального напряженного состояния, помимо деформации, может произойти его поворот на некоторый угол. Этот поворот не будет влиять на рост напряжений, но первоначальное состояние этого элемента, которое характеризуется переменными (Sxnx , Syny , Txny ), поворачивается на определенный угол. Поскольку уравнения движения записаны для конкретной системы координат, то повернутые напряжения должны быть пересчитаны и приведены к этой системе координат. • Скорости деформаций:

д x c д x д y д y

E xx

*

^E yy

д y д x c

E _--1--.

д x д y

Точка над параметром означает производную по времени для фиксированной частицы.

• 5.    Гидростатическое давление (сила давления жидкости на единицу площади):

• 6.    Условие текучести Мизеса, необходимое для учета предела упругости. Это условие задает границу, отделяющую область пластического состояния материала от области упругого состояния:

  ( 5 12 + 5 22 + 5 32 ) - -( Y ⁰) < 0,

  
  
  
  

  где Y ⁰ жения

  
  

  – предел текучести для простого растя-(напряжение при котором начинает раз-

• виваться пластическая деформация), который может быть как константой (для идеально-пластических сред), так и некоторой функцией (для анизотропных материалов, то есть материалов с упрочнением).

P = a (n -1) + b(n —1)2 + c(n —1)3 + d^E, (14)

n=—

V a, b, c – постоянные, при которых давление P(n) превышает предел упругости.

Для корректного применения конечно-разностной схемы метода необходимо записать выражения в частных производных для заданной точки пространства в данный момент времени. Подробное описание конечно-разностных уравнений в данной работе опускается, и на приведенных ниже рисунках показаны результаты применения рассматриваемого метода к конкретной задаче.

В качестве преграды в нашем случае рассматривается биологическая ткань, моделируемая описанным методом с заданием необходимых физико-механических характеристик, типичных для мягких тканей [5]: плотность ρ = 1000 кг/м³, скорость звука = 1600 м/с, модуль объемного сжатия K = p c 2 = 25.6^10 8 Па, а также предел упругости, модуль Юнга и другие.

Моделируемая область представлена в виде регулярной (равномерной) сетки с квадратными ячейками. Так как задача является осесимметричной, рассматривается только одна (правая) половина моделируемой области.

x

y

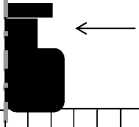
ударник

R

неподвижная граница

Z

свободная поверхность

ВЕСТНИК 2014. ВЫПУСК 4

Рис. 1. Графическая модель задачи (начальная конфигурация регулярной лагранжевой сетки с ударником)

Начальные условия:

Размер расчетной области по оси z – 5 см.

Размер расчетной области по оси R – 20 см.

Масса ударника – 12 г.

Радиус ударника – 7,65 мм.

Предполагается, что ударник недеформи-руемый, а узлы сетки ячеек, расположенных под ударником, двигаются со скоростью ударника вдоль оси z (по вертикали). Горизонтальные скорости этих узлов считаются равными нулю. Ударник имеет форму цилиндра и считается не-деформируемым.

Скорость ударника после взаимодействия с преградой рассчитывается по второму закону Ньютона [6; 7]. Размер области по глубине (4 см)

задается исходя из средней суммарной толщины кожи, подкожной клетчатки, мышц и жировой ткани тела человека в области наиболее уязвимых внутренних органов (печени, легких, селезенки). Начальная скорость ударника составляет 100 м/с, что соответствует штатной скорости пули (энергия пули ≈ 70 Дж).

Результаты расчетов и их обсуждение

Основные расчёты проводились на регулярных (равномерных) сетках. Характеристики, представляющие основной интерес, – это новые координаты узлов расчетной сетки. Их можно получить в виде изображений деформируемой области. Как выяснилось, основные внутренние процессы происходят вблизи оси симметрии, следовательно, всю свободную поверхность, показанную на рис. 1, можно не учитывать. Поэтому в дальнейшем будет показана только часть расчетной области по радиальной координате (оси R).

Приложение для исследования полей давления и деформаций, возникающих в рамках поставленной задачи, представляет собой программу, написанную на языке Object Pascal в среде разработки Delphi 7 [10].

Поскольку программа моделирует динамический процесс, можно исследовать разные ситуации, получая нужные характеристики в любой момент времени. Естественно, максимальное давление будет возникать в первом слое ячеек, контактирующих с ударником, главным образом – в первой ячейке относительно оси симметрии (закрашенная ячейка на рис. 2).

Ниже приведены результаты расчетов, показывающие характер изменения давления в деформируемой области и скорости ударника с течением времени.

ВЕСТНИК 2014. ВЫПУСК 4

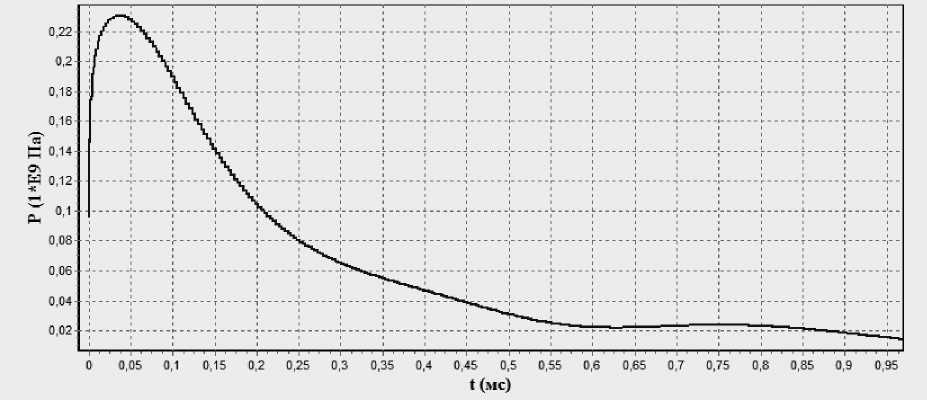
Рис. 3. Изменение давления во времени (в закрашенной ячейке)

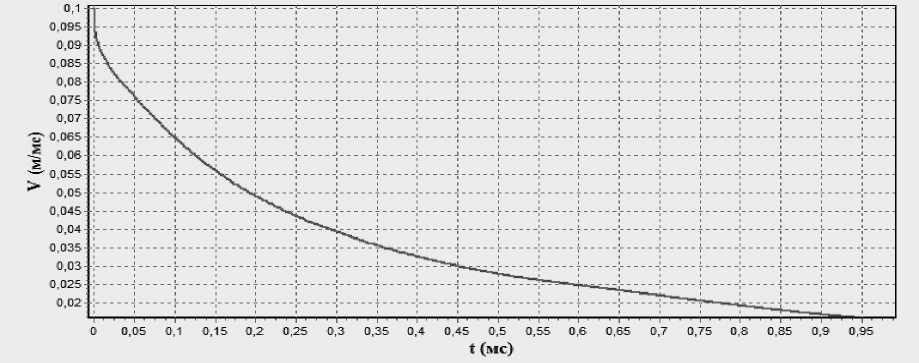
Рис. 4. Зависимость уменьшения скорости ударника от времени в результате торможения при ударе

Существенным достоинством используемого подхода является возможность наблюдения динамики распространения деформации в тканях с заданными характеристиками. При этом оказалось возможным визуализировать как образование гематомы, так и размозжение тканей с образованием так называемой откольной тарелки [8], которая является достаточно объективной характеристикой динамической прочности материала на растяжение в микросекундном диапазоне длительности действия нагрузки [9]. Откольное разрушение материала (возникновение отколь-ной тарелки) является результатом интерференции волны нагрузки (сжатия) и отраженной волны разгрузки (растяжения), распространяющихся навстречу друг другу. При определенном соотношении между толщинами ударника и преграды внутри нее создаются растягивающие напряжения, приводящие к указанному эффекту.

Основным вопросом при разработке и применении травматического оружия является вопрос о возникновении поражений наружных покровов, тканей и внутренних органов. Поражение органов происходит при пробитии наружных покровов.

Как уже отмечалось, наша программа, основанная на лагранжевом подходе к описанию движения, не может полноценно использоваться для расчета процесса проникания из-за очень больших деформаций лагранжевой сетки. Однако, как оказалось, на основе такой программы можно косвенно выявить характер такого процесса при соответствующих уровнях нагрузок, действующих в биологических тканях при ударе.

На рис. 5 (а) выделена область мягкой ткани, в которой максимальное давление при ударе превосходит 107 Па. Считается, что такого давления достаточно для разрушения кровеносных сосудов и образования гематомы (синяка). Естественной мерой интенсивности травматического воздействия может служить максимальный объем гематомы. На рис. 5 (б) показано расчетное изменение объема гематомы во времени до достижения максимального значения.

Кроме подкожной гематомы другим видом повреждения мягких тканей (более тяжелым по последствиям) является их размозжение при ударе. Для оценки возможности такого повреждения, по результатам расчетов, находилась область, в которой растягивающие напряжения, появляющиеся при отражении ударной волны сжатия от внутренней поверхности мягких тканей, превосходили 50∙105 Па. Такая величина заведомо превосходит предел прочности мягких

а)

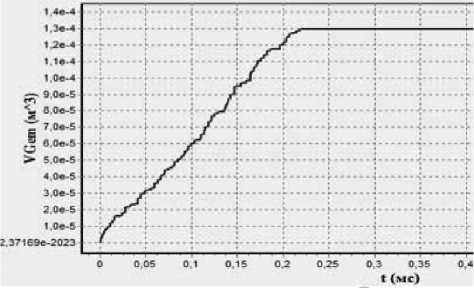
б)

Рис. 5. Вид модели гематомы в момент времени t = 0,22 мс. (а) и изменение ее объема с течением времени (б)

тканей на разрыв. Указанная область растяжения имеет классический вид откольной тарелки (рис. 6).

Область смятия тканей (область гематомы) рис. 5(а) и область разрушения тканей разрывом рис. 6, во-первых, пересекаются, а во-вторых, в совокупности простираются практически на всю толщину мягких тканей (4 см). Это свидетельствует о том, что при заданных расчетных параметрах удара мягкие покровные ткани под-

ВЕСТНИК 2014. ВЫПУСК 4

ВЕСТНИК 2014. ВЫПУСК 4

Таким образом, результаты моделирования подтверждают исходную гипотезу об эффективности применения указанного метода для исследования полей давления и деформаций в биологических тканях. По крайней мере, на качественном уровне они вполне соответствуют практическим данным, отражаемым статистикой применения травматического оружия. Очевидный интерес представляет проведение более детального исследования, в том числе – на количественном уровне с подбором оптимальных параметров расчетной сетки.

Авторы благодарят Л.С. Евтерева за обсуждение задачи и результатов исследования.