Распределение расстояний между точечными геологическими объектами

Теория вероятностей и математическая статистика успешно применяются в различных областях геологической науки: при обработке минералогических, геохимических и петрохимических данных, установлении законов частотного распределения наблюдаемых геологических величин. Вместе с тем традиционные методы выявления закономерностей размещения геологических объектов в большинстве случаев имеют приближенный, качественный характер (из-за визуального анализа положения геологических объектов на различных картах и текстовой информации). Причина этого заключается в почти полном отсутствии математических основ такого анализа. В данной работе анализируются свойства многомерного пространства с евклидовой метрикой. Результаты исследований могут использоваться в таких областях знаний, как геология, география, биология.

Предметом исследований служили для нас расстояния между точками в парах, размещенными случайным образом. При этом под случайным распределением понимается такое, при котором все компоненты координат всех точек независимы друг от друга и распределены по равномерному (прямоугольному) закону. Это распределение есть не что иное, как распределение длин отрезков , случайно расположенных в пространстве. При этом нельзя рассматривать пространство вообще, т. е. не ограниченное никакими пределами: в этом случае основные статистики — математическое ожидание и дисперсия — обратятся в бесконечность. Для получения содержательных сопоставимых результатов нами рассматривалось пространство, ограниченное единичным nD-мерным кубом (гиперкубом), превращающимся при nD = 1 в отрезок, при nD = 2 — в квадрат, при nD = 3 — в обычный куб. Все расстояния нормировались на длину диагонали nD-мерного гиперкуба, т. е. на величину ^JnD, где nD — размерность пространства. Этим достигалась сравнимость распределения длин отрезков и независимость статистик от размерности пространства (как выяснилось, только в первом приближении).

Основой для теоретического анализа распределения длин случайных отрезков служит тот очевидный факт, подтверждаемый экспериментально, что для отрезка ( nD = 1) плотность распределения линейно уменьшается до нуля с увеличением длины исследуемого отрезка x :

g(x) = 1 — x . (1)

Из условия нормировки (интеграл плотности вероятности

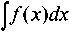
о должен быть равен 1) получаем

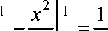
о 2 0 2 ’

1                  1

Jg(x) = J(1 - x^dx = х о         о откуда плотность вероятности f(x) равна

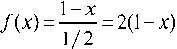
Математическое ожидание M ( x ) и дисперсия D ( x ) расстояний (длин отрезков) в одномерном случае равны 1

М (х) = Jx • / (х)г/х = о

1                                       1

J2(l - x)xdx = — = 0.(3);

о

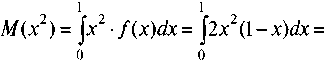
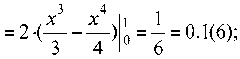
Д(х) = М(х2)-ЛТ2(х) =

6 з'з

18 18

— = 0.055(5);

<т(х) = ^D(x) = 0.236.

Для размерностей пространства nD > 1 случайная величина, т. е. расстояние между точками в паре (или, другими словами, длина случайного отрезка), есть корень квадратный из суммы квадратов разностей одноименных компонент координат:

x = ^(z/1-v1)2 + (z/2-v2)2+...+ 77777^,     (3)

где и и v — компоненты координат 1, 2,.., nD точек в паре и и v .

Если бы компоненты координат были распределены по гауссовскому закону N (0, 1), то из этого сразу вытекало бы, что распределение расстояний в многомерном пространстве подчиняется закону д^? = X (закону х). Но распределение точек в пространстве нельзя осуществить по нормальному закону случайно: необходимо было бы выбрать точку концентрации и меру рассеивания. Единственно возможный вариант — равномерное (прямоугольное) распределение каждой компоненты на отрезке (0, 1) — стороне единичного гиперкуба. Это наводит на мысль о том, что распределение длин случайных отрезков, нормированных

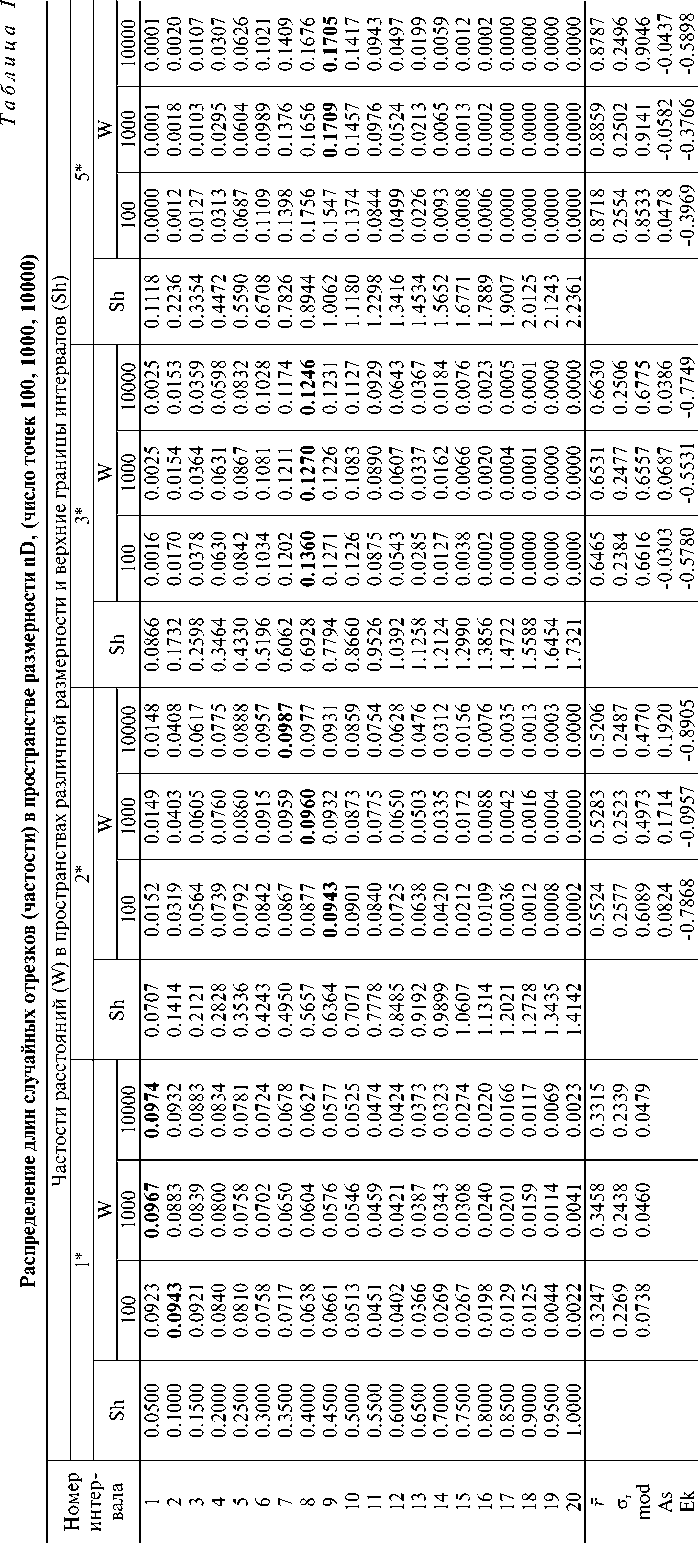
Пр о д о л ж е и и е т а бл и ц ы 1

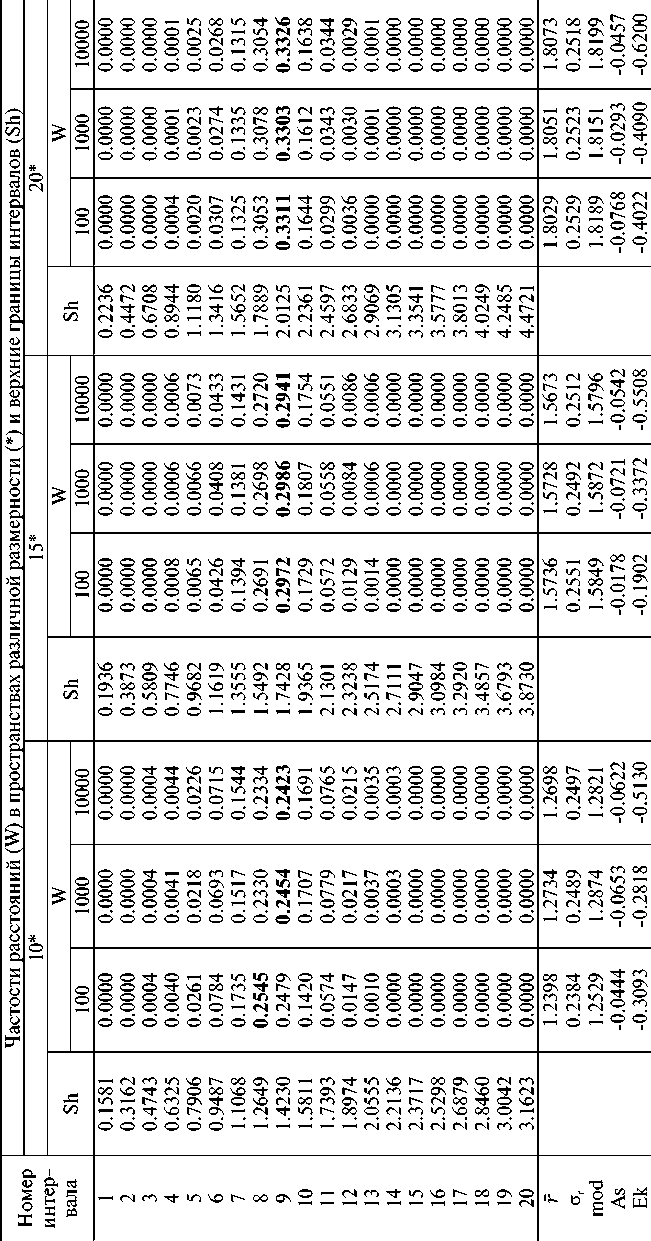
Примечание. Жирным шрифтом выделены максимальные значения.

по стороне или диагонали гиперкуба, следует не подгонять под другие распределения, а считать оригинальным, самостоятельным распределением, генерируемым распределением суммы квадратов случайных величин, равномерно распределенных на отрезке (0, 1), т. е. некоторым аналогом распределения х — основой анализа распределения точек в пространстве.

Моделирование велось по авторской программе, чтобы получить основу для дальнейших исследований, в том числе для сравнения с ним всех модификаций других распределений. Прежде всего было установлено, что число точек не влияет на центральные моменты, т. е. на такие статистики, как математическое ожидание расстояния, его дисперсия, асимметрия и эксцесс, тем самым и на форму распределения . Сначала этот факт кажется парадоксальным: плотность точек увеличивается, а расстояния между ними остаются неизменными. Однако очевидно, что добавление n +1-й точки в гиперкуб образует n новых пар, т. е. новых отрезков, которые в силу случайного распределения n предыдущих точек будут распределены так же, как и предыдущие пары.

Оценки статистик и частостей в гистограммах случайным образом колеблются, и тем сильнее, чем меньше точек, но их средние значения с увеличением числа точек не меняются. При числе точек 100 они стабилизируются, а при 500 становятся практически постоянными. Дальнейшее увеличение числа точек сильно увеличивает время счета, но мало изменяет точность: число расстояний увеличивается как n2.

Моделирование на отрезке ( nD = 1) показало полную сходимость модельного среднего расстояния с теоретическим, т. е. со значением г = 0.3333, M ( r ) = 0.(3), а также сходимость модельного среднего квадратического отклонения с теоретическим значением Sr = 0.24, о _r = 0.236 (табл. 1). Частоты гистограммы строго линейно уменьшаются до нуля с увеличением r до 1. Это создает уверенность в правильности моделирования, так как для размерности пространства 2 и более используется то же самое ядро программы.

Совсем другая картина наблюдается в изменении статистик с увеличением размерности пространства. Поскольку мы нормировали расстояния на длину диагонали гиперкуба, которая увеличивается с увеличением nD , то предполагалось, что математическое ожидание расстояния не будет зависеть от nD . Так в первом приближении и оказалось (табл. 2). Однако все-таки наблюдается незначительное увеличение (на 21%) среднего расстояния и его нельзя квалифицировать как неточность оценки: объем выборки

(число пар расстояний) при 500 модельных точках составляет 124 750. Точная причина этого нам пока неизвестна. Вероятно, что увеличение размерности пространства расширяет его удельный объем так, что возрастает вероятность появления пар точек с большими расстояниями между ними.

В изменении среднего квадратического расстояния наблюдается интереснейшая картина. С одной стороны, увеличение доли больших расстояний должно увеличивать значение о_r . С другой стороны, необходимо помнить, что при увеличении размерности пространства пропорционально увеличивается число случайных слагаемых — компонент координаты. Итоговую случайную величину мы делим при нормировании на фпВ , что в результате приводит к уменьшению среднего квадратического отклонения пропорционально этой величине. Так, при nD = 1 о _r = 0.242, а при nD = 20 она должна быть 0.242/720 = 0.054. Оценка по данным моделирования равна 0.056!

С увеличением размерности пространства сильно меняется форма данного распределения. В случае nD = 1 гистограмма будет линейной, монотонно убывающей слева направо. Начиная с nD = 2 кривая становится колоколообразной одномодальной, сильно асимметричной и плосковершинной по сравнению

Т а б л и ц а 2

Распределение длин случайных отрезков (частости) в пространстве размерности nD, нормированных по диагонали единичного гиперкуба (число точек 500)

Номер интервала	Верхняя граница интервала	Размерность пространства nD
		1	2	3	5	10	15	20
1	0.0500	0.0949	0.0148	0.0026	0.0000	0.0000	0.0000	0.0000
2	0.1000	0.0904	0.0426	0.0155	0.0021	0.0000	0.0000	0.0000
3	0.1500	0.0854	0.0659	0.0369	0.0118	0.0004	0.0000	0.0000
4	0.2000	0.0802	0.0838	0.0632	0.0340	0.0047	0.0006	0.0001
5	0.2500	0.0759	0.0956	0.0867	0.0709	0.0230	0.0074	0.0025
6	0.3000	0.0694	0.1041	0.1066	0.1124	0.0746	0.0431	0.0269
7	0.3500	0.0669	0.1035	0.1213	0.1507	0.1596	0.1415	0.1320
8	0.4000	0.0620	0.1005	0.1297	0.1730	0.2354	0.2721	0.3066
9	0.4500	0.0574	0.0933	0.1235	0.1677	0.2377	0.2906	0.3313
10	0.5000	0.0528	0.0818	0.1105	0.1308	0.1657	0.1767	0.1632
11	0.5500	0.0473	0.0686	0.0903	0.0820	0.0736	0.0571	0.0347
12	0.6000	0.0430	0.0550	0.0586	0.0422	0.0213	0.0099	0.0027
13	0.6500	0.0377	0.0407	0.0322	0.0162	0.0035	0.0009	0.0001
14	0.7000	0.0333	0.0266	0.0148	0.0048	0.0004	0.0000	0.0000
15	0.7500	0.0300	0.0131	0.0058	0.0011	0.0000	0.0000	0.0000
16	0.8000	0.0250	0.0061	0.0015	0.0001	0.0000	0.0000	0.0000
17	0.8500	0.0201	0.0026	0.0003	0.0000	0.0000	0.0000	0.0000
18	0.9000	0.0142	0.0011	0.0000	0.0000	0.0000	0.0000	0.0000
19	0.9500	0.0102	0.0003	0.0000	0.0000	0.0000	0.0000	0.0000
20	1.0000	0.0037	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
Г		0.3433	0.3551	0.3756	0.3833	0.3998	0.4054	0.4040
ч		0.2417	0.1714	0.1415	0.1104	0.0793	0.0655	0.0563
mod		0.0250	0.2750	0.3750	0.3750	0.4250	0.4250	0.4250
med		0.3250	0.3250	0.3750	0.3750	0.4250	0.4250	0.4250
As			0.2644	0.0400	0.0082	-0.0391	-0.0319	-0.0456
Ek			-0.5499	-0.5028	-0.2682	-0.0985	-0.0310	-0.0466
Zz2			3459.0486	1677.6348	474.0244	100.1063	34.6857	57.1557

с гауссовской кривой, однако с увеличением nD от трех и до 20 кривая плотности вероятности будет совершенно симметричной ( As = —0.046) и «нормально» плосковершинной ( Ek = —0.047). Эта картина вполне объясняется центральной предельной теоремой: стремление к нормальности — следствие суммирования все большего числа компонент координат точек при увеличении размерности пространства (см. рис. 1).

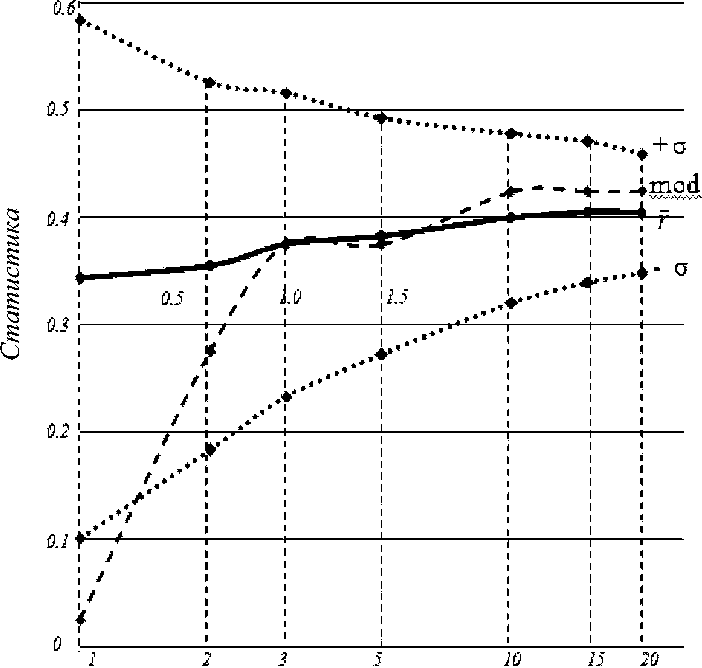
В табл. 3 и на рис. 2 компактно представлена изложенная выше и другая информация, из которой наиболее любопытным является тот факт, что коэффициент вариации (показатель, широко применяемый в геолог ии) , нормированный на величину ^nD , постоянен и независим от nD и составляет около 70 %.

Мы исследовали два совершенно разных объекта. Первым из них была облицовочная плитка керамогранита, содержащая на фоне смеси светлых ингредиентов много мелких черных вкраплений (рис. 3). Расположение этих вкраплений было перенесено на кальку и сняты их координаты. В пределах исследуемого нами квадрата оказалось 575 таких зерен. Результаты обработки по нашему программному комплексу представлены в табл. 4 и рис. 4. Сравнение табл. 4 с табл. 2 свидетельствует об идентичности распределений. Еще нагляднее это видно при сопоставлении гистограмм на рис. 4 и на рис. 1.

Таким образом, мы имеем теперь надежный критерий отнесения распределения точек к случайному. Судя по рис. 3, темноцветные вкрапления имеют некоторую тенденцию к группировке. Однако наш статистический анализ показал, что количество и плотность сгущений не выходит за пределы случайных флуктуаций плотности. Этого и следовало ожидать, так как плитки получают после тщательного перемешивания исходного материала.

Второй пример — распределение 747 горных вершин одного из участков Приполярного Урала (рис. 5). Логика подсказывает, что вершины должны обнаруживать тенденцию к линейной группировке вдоль водораздельных линий хребтов.

Статистический анализ по программам созданного нами комплекса показал, что распределение расстояний между вершинами похоже на типовую кривую случайного распределения для nD = 2. Тенденция к линейной группировке выражается в увеличении частот в левых интервалах (с малыми расстояниями!) гистограммы (табл. 4 и 2). «Перегрузка» левых интервалов «уравновешивается» перегрузкой крайних правых. В итоге распределение характеризует-

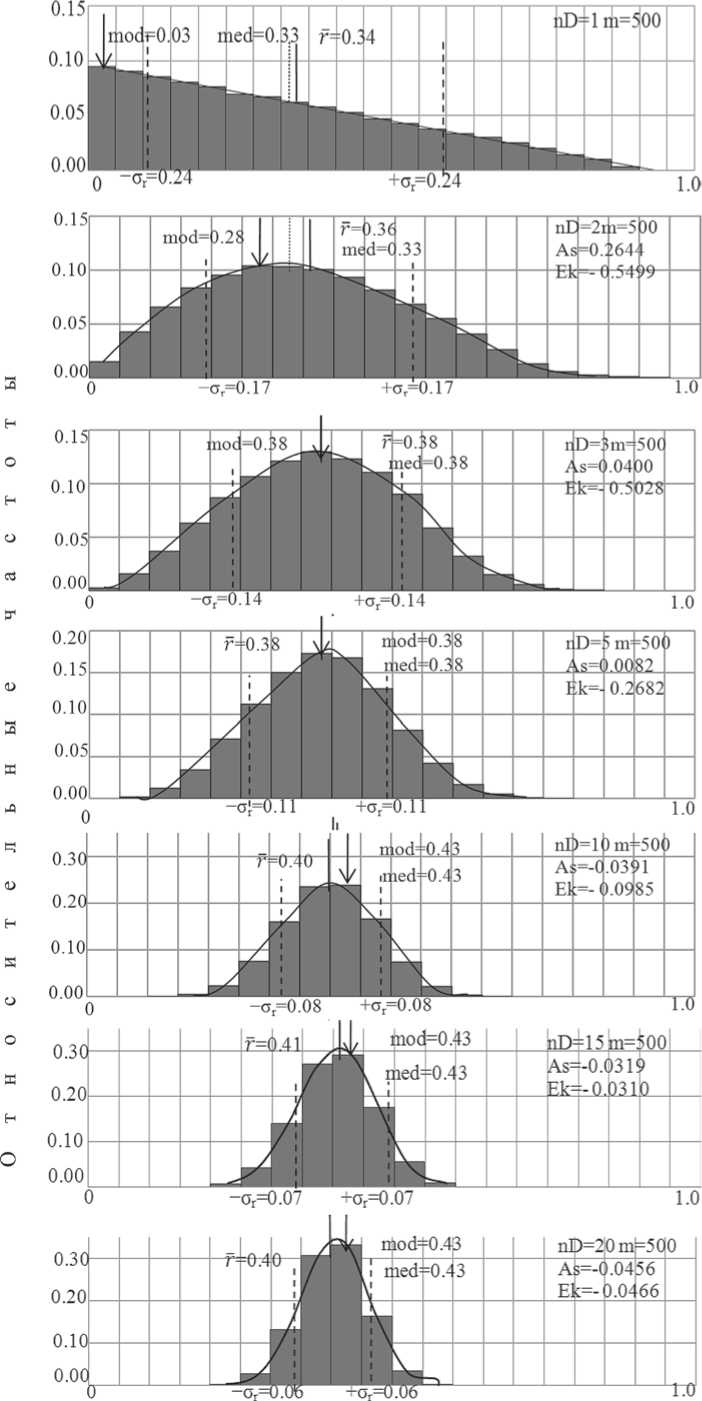
Рис. 1. Гистограммы распределения длин отрезков в пространствах размерности 1, 2, 3, 5, 10, 15, 20, нормированных по диагонали единичного гиперкуба

Т а б л и ц а 3

Статистические показатели распределения расстояний между случайно расположенными точками (длин случайных отрезков) в зависимости от размерности пространства (500 точек)

Показатель	Размерность пространства пВ
	1	2	3	5	10	15	20
Г	0.343	0.355	0.376	0.383	0.400	0.405	0.404
<зг	0.242	0.171	0.141	0.110	0.079	0.066	0.056
As	—	0.264	0.040	0.008	-0.039	-0.032	-0.046
Ек	—	-0.550	-0.503	-0.268	-0.098	-0.031	-0.047
V, %	71	47	37	29	20	17	15
v-JnD,%	71	67	64	65	63	66	67

Т а б л и ц а 4 Распределение расстояний между темноцветными вкраплениями на плитке керамогранита (число точек 575), нормированных по диагонали единичного квадрата

Номер интервала	Верхняя граница интервала	Частость расстояний
		nD2
1	0.0500	0.0149
2	0.1000	0.0411
3	0.1500	0.0601
4	0.2000	0.0748
5	0.2500	0.0837
6	0.3000	0.0896
7	0.3500	0.0960
8	0.4000	0.0950
9	0.4500	0.0925
10	0.5000	0.0885
И	0.5500	0.0796
12	0.6000	0.0679
13	0.6500	0.0522
14	0.7000	0.0334
15	0.7500	0.0169
16	0.8000	0.0087
17	0.8500	0.0036
18	0.9000	0.0012
19	0.9500	0.0002
20	1.0000	0.0000
Г		0.3749
6Г		0.1782
mod		0.3250
med		0.3750
As		0.1346
Ek		-0.7011

^гт^нжриь цг.гжи^

Рис. 2. Изменение средней длины отрезков между 500 точками при случайном их размещении в зависимости от размерности пространства от 1 до 20)

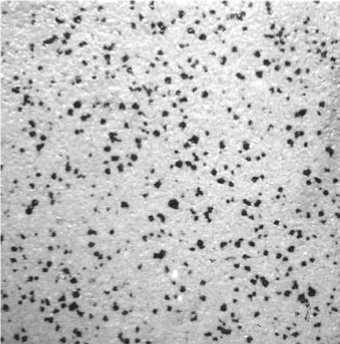
Рис. 3. Участок плитки керамогранита с темноцветными вкраплениями ингредиентов

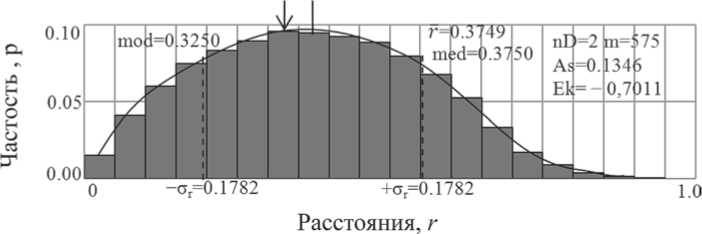
Рис. 4. Распределение расстояний между темноцветными вкраплениями на плитке керамогранита

Т а б л и ц а 5

Распределение расстояний между горными вершинами Приполярного Урала (северной части национального парка «Югыд-Ва», М. 1:200 000) в двумерном пространстве, нормированных по диагонали единичного квадрата (число вершин 747)

Номер интервала Верхняя ãраница интервала Частость расстояний nD2 1 0.0500 0.0168 2 0.1000 0.0446 3 0.1500 0.0652 4 0.2000 0.0783 5 0.2500 0.0858 6 0.3000 0.0918 7 0.3500 0.0948 8 0.4000 0.0944 9 0.4500 0.0901 10 0.5000 0.0831 11 0.5500 0.0749 12 0.6000 0.0630 13 0.6500 0.0502 14 0.7000 0.0335 15 0.7500 0.0178 16 0.8000 0.0094 17 0.8500 0.0042 18 0.9000 0.0017 19 0.9500 0.0004 20 1.0000 0.0000 f 0.3692 σr 0.1812 mod 0.3250 med 0.3750 As 0.1980 Ek –0.6749 г = 29.536 км; ar = 14.496 км; mod = 26.0 км; med = 30.0 км.

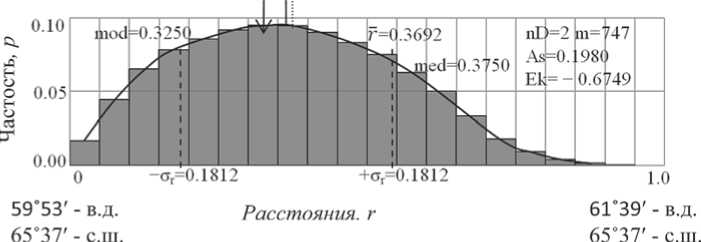
Рис. 5. Участок физической карты Приполярного Урала в пределах, указанных по углам координат. Точки — горные вершины. М-б 1:200 000

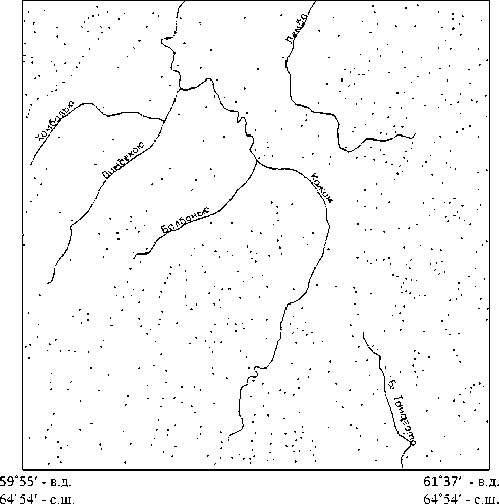
Рис. 6. Распределение расстояний между горными вершинами участка Приполярного Урала

ся большим средним квадратическим отклонением, лучшей симметричностью и большей плосковершинно-стью (рис. 6). Однако эти не очень контрастные отличия не могут служить надежными критериями тенденции к линейной группировке, что заставило нас перейти к анализу так называемых порядковых расстояний.

Благодарю Ю. А. Ткачева за идеи и неоценимую помощь в проведении исследований.