Распределенное имитационное моделирование системы теплоснабжения зданий в среде VisSim

Сегодня для управления большими сложными системами все чаще используются имитационные модели. Такие модели зачастую представляют собой сложные системы нелинейных уравнений с большим количеством неизвестных, для нахождения которых требуется выполнение большого объема вычислений. При этом вычислительных мощностей процессора и оперативной памяти отдельных ЭВМ уже недостаточно для обеспечения процесса расчета. Поэтому для решения таких систем становятся все более актуальными разработка и применение методов распределенных и параллельных вычислений. При этом развиваются преимущественно два направления распределенного имитационного моделирования:

• 1.    Разработка решателей систем нелинейных уравнений, позволяющих распределить сам процесс решения единой сложной системы уравнений между ЭВМ. При развитии этого направления наряду с математическими методами активно применяются методы параллельного программирования.

• 2.    Разработка методов модификации моделей, направленная на изменение структуры и параметров модели таким образом, чтобы ее было возможно рассчитывать параллельно на нескольких ЭВМ или ядрах процессора.

В рамках первого направления актуальными и перспективными задачами являются разработка и совершенствование методов распараллеливания неявных решателей, используемых для решения систем нелинейных и дифференциальных уравнений [1, 2]. Однако такие решатели зачастую разрабатываются для узкоспециализированного ПО, которое предназначено в основном для исследовательских задач и зачастую не обладает удобными инструментами построения имитационных моделей в виде блок-схем и стандартизованными средствами сопряжения со SCADA-системами. Напротив, в наиболее распространенных средах ( VisSim, Matlab Simulink ), являющихся типовыми решениями для имитационного моделирования, все еще отсутствуют инструменты, позволяющие распараллелить процесс решения системы уравнений модели, составленной в виде пользовательской блок-схемы. Ввиду этого, достаточное внимание уделяется и второму направлению.

При модификации моделей наиболее распространенными методами распределения вычислений являются эквивалентирование и разделение на подсистемы. Эти методы получили развитие при моделировании электрических схем и сетей [3]. Однако хотя эквивалентирование и позволяет рассчитать определенные значимые параметры системы, в общем случае оно не отражает реальную структуру системы, и применение его для определенных систем просто невозможно.

Метод разделения на подсистемы не зависит от решателя, используемого той или иной средой моделирования. Поскольку подсистемы моделируются в отдельных процессах, то распарал- леливание самого процесса решения уже не является столь необходимым. Кроме того, этот метод менее зависим от структуры системы по сравнению с эквивалентированием.

Сегодня все более актуаль ным становится макромоделирование слож ных систем энерг о снабжения, и теплоснабжения в частности как одной из подсистем. Рассм отрим возможность применения м етода разделения на подсистемы на примере имитационной м одели теплоснабж ения зданий.

Принцип построения распределенной имитационной модели

Модель теплоснабжения зда ний может быть достаточно большой или отдельные ее блоки могут быть достаточно сложными, но в общем случае в системе есть источники, соединительные элементы (трубопроводы, трубопроводные тройники и т. д.) и потребители. Рассмотрим принцип разбиения модели, построенной , например, в среде имитационного модели рования VisSim согласно методике, описанной в [4, 5] (рис. 1).

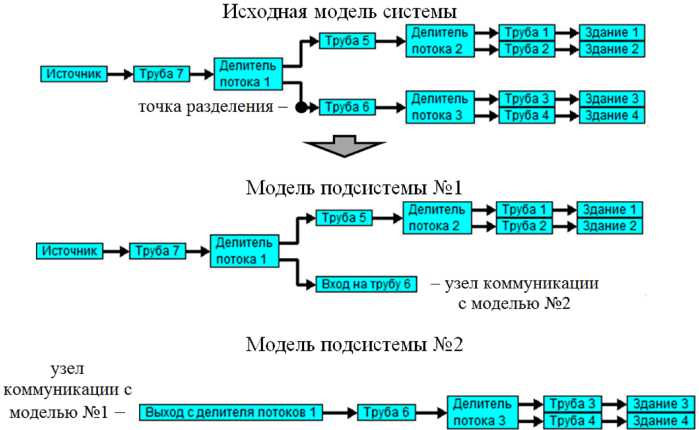
Рис. 1. Структурное разделение исходной модели на подсистемы

Выбираем точку разделения исходной модели на 2 части. При этом каж дая часть станет о т дельной моделью и будет выпол няться в отдельном процессе. В каждой ново й модели соответст вующая недостающая часть заме няется узлом коммуникации. В первой моде ли узел коммуник а ции выполняет функцию потребителя, во второй модели – функцию источника. Рассмотрим эти узлы коммуникации (рис. 2).

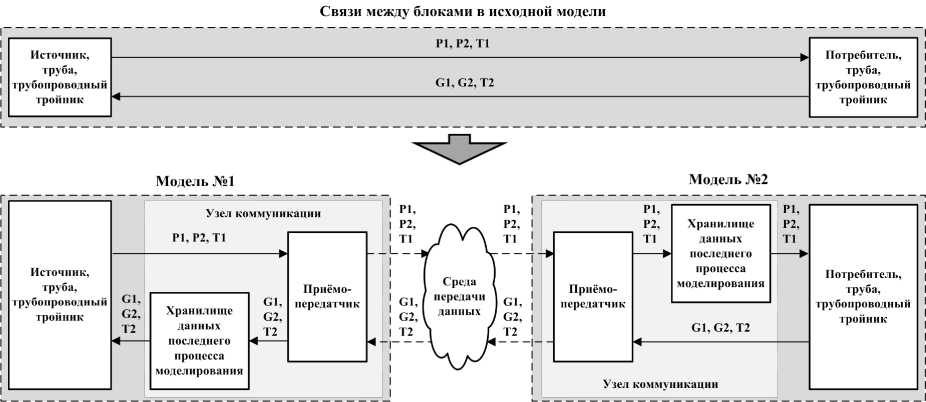
Рис. 2. Функциональное разделение исходной модели на подсистемы

Изначально имеем информационные связи между частями модели из 6 переменных. Это температуры, давления и расходы в подающем и обратном трубопроводах.

Для первой модели узел коммуникации представляет собой потребителя. На узел коммуникации как на потребителя подается теплоноситель с определенной температурой T 1 и известным перепадом давлений P 1 и P 2. Эти данные передаются узлом коммуникации первой модели в узел коммуникации второй модели, например, через ЛВС с использованием стека протокола TCP/IP . Во второй модели узел коммуникации является источником с уже известными характеристиками (принятыми из первой модели P 1, P 2 и T 1), на основании которых во второй модели производится расчет расходов теплоносителя G 1 и G 2 и температуры теплоносителя в возвращающем трубопроводе T 2, что и характеризует вторую модель как потребителя. В свою очередь, рассчитанные параметры передаются узлом коммуникации второй модели в узел коммуникации первой. И на основе информации о второй модели как о потребителе происходит пересчет параметров тепловой сети в первой модели.

Блок хранилища данных применяется для хранения данных, полученных в результате предыдущего процесса моделирования. Поскольку части модели запускаются асинхронно, эти блоки позволяют для первого шага моделирования получать последнее состояние соответствующих подсистем.

Математически система нелинейных уравнений была разделена на 2 части. При этом модифицировались все уравнения, в которых участвовали 6 переменных исходной связи. Остальные уравнения были разделены между частями модели.

При этом таким способом можно разделить модель на несколько частей. Однако в результате того, что модели будут выполняться в разных процессах, их необходимо синхронизировать. Рассмотрим 2 подхода к управлению синхронизацией, которые могут быть применены при использовании метода разделения на подсистемы.

Синхронизация процессов моделирования подсистем

Первый подход заключается в том, что расчет всех частей модели проводится в реальном времени с одинаковой длительностью шага моделирования. В этом случае на каждом шаге происходит передача результатов моделирования между частями, но из-за одинаковой длительности шагов каждой модели общего рассогласования не происходит.

Отметим преимущества данного подхода:

• -    простота реализации (только настройка параметров проекта в среде моделирования);

• -    нет задержек при моделировании частей системы и системы в целом, связанных с ожиданием данных;

• -    время передачи данных не влияет на время расчета модели.

Недостатки этого подхода заключаются в следующем:

• -    при подборе длительности шага моделирования необходимо учитывать структуру модели и количество элементарных вычислительных блоков;

• -    необходимо подбирать временной запас шага моделирования из-за возможного увеличения длительности расчета отдельного шага при переходных процессах;

• -    расчет на каждом шаге моделей с малой реальной длительностью шага растягивается до величины глобального шага.

Второй подход заключается во введении подсистемы синхронизации частей модели, которая должна обеспечивать ожидание результатов моделирования каждого шага всех частей перед обменом данными между ними и вычислением следующего шага.

Преимущества данного подхода – это то, что:

• -    каждая модель рассчитывается в собственном модельном времени;

• -    ввиду этого при наличии синхронизатора нет необходимости расчета и ввода временного запаса;

• -    процесс синхронизации не зависит от длительности расчета шагов частей модели.

Недостатки этого подхода заключаются в том, что:

• -    модель усложняется дополнительными блоками синхронизации;

• -    время расчета модели зависит от времени передачи данных;

• -    части модели с малой длительностью шага моделирования простаивают в ожидании такта синхронизации.

Стоит отметить, что оба подхода являются жизнеспособными и в различных ситуациях обеспечивают требуемые параметры синхронизации расчета.

Результаты моделирования

Описанный подход был исследован на базе модели системы теплоснабжения ФГБОУ ВПО «Южно-Уральский государственный университет» (НИУ) [5]. В ходе экспериментального моделирования на ЭВМ с использованием 2 ядер с частотой 2,3 ГГц процессора AMD A10-4600M при разбиении статической модели, построенной в среде VisSim, на 2 подсистемы с применением подсистемы синхронизации были получены результаты, представленные в таблице и на графике (рис. 3). Модуль синхронизации в модели подсистемы № 1 состоит из 400 элементарных вычислительных блоков. Модуль синхронизации в модели подсистемы № 2 – из 120 блоков. В таблице число блоков в подсистемах указано без учета блоков модулей синхронизации. В ходе каждого эксперимента было произведено 10000 шагов моделирования. Для увеличения количества блоков в экспериментах система дополнялась однотипными группами объектов, состоящих из потребителей, трубопроводов и трубопроводных тройников.

Результаты моделирования

Число функциональных блоков в исходной системе	Время выполнения исходной системы, с	Число блоков в подсистеме № 1	Число блоков в подсистеме № 2	Время выполнения при разделении, с
2500	14,7	1300	1200	83,4
5000	58,7	2600	2400	98,5
7500	207,2	3800	3700	133,4
10000	583,0	5000	5000	143,7
12500	1229,8	6200	6300	314,4

Согласно графику (рис. 3), время расчета исходной модели с увеличением количества блоков возрастает быстрее, чем время расчета модели, разделенной на подсистемы. Это связано не только с тем, что каждая подсистема рассчитывается в отдельном процессе, но и с тем, что в каждой подсистеме меньше и элементарных вычислительных блоков, и решаемых на каждом шаге моделирования уравнений.

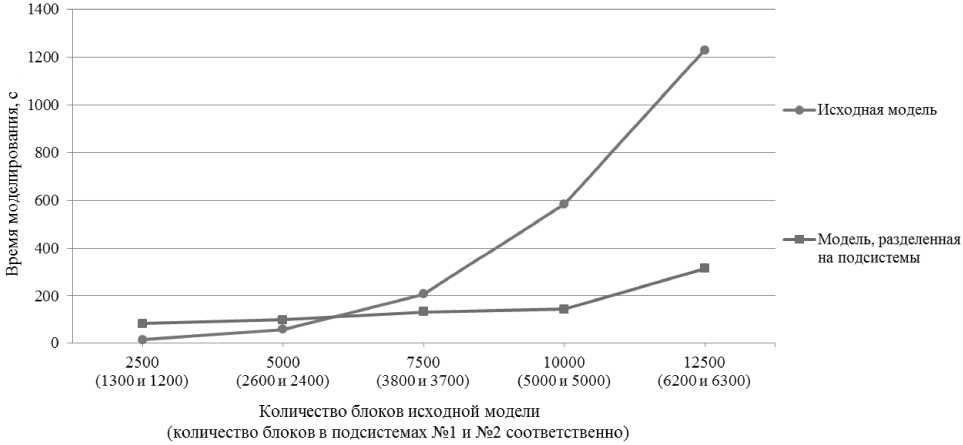
Рис. 3. Результаты моделирования

Заметим, что для исходных систем с количеством блоков 2500 и 5000 разбиение на подсистемы нецелесообразно, поскольку в этих случаях на каждом шаге моделирования время обмена данными между подсистемами больше времени расчета каждой подсистемы.

Заключение

Таким образом, представленный подход к распределению вычислений позволяет повышать скорость численного моделирования больших систем за счет построения взаимосвязанных систем нелинейных уравнений, результаты синхронизированного решения которых эквивалентны решению системы уравнений в исходной модели.

Применение описанного подхода позволяет строить новые модели и модифицировать уже существующие так, чтобы их было возможно интегрировать в системы управления, которые требуют высокую скорость вычислений параметров.

Стоит также отметить то, что сходимость расчета у каждой подсистемы в отдельности лучше, чем у исходной системы, ввиду большего числа уравнений в исходной системе. Однако из-за расхождения результатов вычислений в пределах одного шага сходимость взаимосвязанного расчета моделей нескольких подсистем может оказаться хуже, чем у исходной системы. Поэтому данный вопрос требует дополнительных исследований.