Распределенный контроль в системах с распределенными параметрами

В работах [1-10] рассмотрена задача оптимального контроля для довольно широкого класса химико-технологических аппаратов. Для линейной математической модели управляемого объекта с постоянными коэффициентами на основе метода преобразования Лапласа получены необходимые условия оптимальности весовых функций распределенного контроля. Это обязательное условие позволяет рассчитать оптимальные весовые функции, дающие предельную оценку распределенного контроля за управляемым процессом.

В данной статье рассматривается непрерывный процесс взаимодействия двух противоточно-движущихся сред в тепломассообменном аппарате с пространственно-распределенным воздействием. Для этого объекта рассмотрена задача оптимального распределенного контроля, управляемый процесс которого описывается дифференциальными уравнениями в частных производных с переменными коэффициентами.

Для решения задачи оптимального контроля применяется метод вариационного исчисления. Полученные необходимые условия оптимальности используются при построении численного метода расчета оптимальных весовых функций распределенного контроля.

Исходя из закона сохранения количества тепла или массы, в рамках гипотез, принятых в работе [11], рассмотрим уравнения, описывающие этот процесс:

dU еЦих

1— К ( X, t ) \U^ — e ) , Ie c^ x e )

где 6 i = 6 i (x, t), i = 1, 2 - функции распределения температуры или концентрации; w i = w(x, t), i = 1, 2 - скорости движения соответственно первой и второй сред; f(x, t) - функция внешнего воздействия.

Здесь внешнее воздействие приложено в m-промежуточных точках и представляется как f (х, t ) = £ Zj( x U( t).

j

В качестве функции распределенного внешнего воздействия принято выражение

^{x (} x ) Atx

b c ( x - x J j^e j

x e ^[ 0, x j ] x ^e[ x j , l ^] ,

где x j - координата точки приложения внешнего воздействия.

j

Система уравнений (1) дополняется начальными и граничными условиями:

6(x, 0) = 0, i = 1, 2,(2)

91 (0, t) = 61 bx(t), 62(l, t) = 62bx(t), где 61bx(t), 62bx(t) - заданные функции; l - длина аппарата, в дальнейшем принимается равной 1. Функционал качества имеет вид

т

J = j[61 (/, t)- 91 (l, t)] dt, где T - фиксированное время процесса управления; 91 (l, t) - заданное значение регулируемой величины; 91(l, t) - выходная (регулируемая) величина.

Используется возможность подачи на объект m + 1 управляющих воздействий: при j = 0 за счет изменения граничных условий на входе второй (регулирующей) среды u₀( t )= 9 _{2 bx} ( t ); при j = 1, ..., m -промежуточных внешних воздействиях и j ( t ).

Таким образом, получаем m + 1-контурную систему автоматического регулирования. Функции управляющих воздействий иj(t) j = 0, .., m представляются в виде tl

" , < t 1 = I u ( t ■ ' > j « 1 < x ^т g j < x 1 dxd " . j = °..... ^m.                                          (5)

• ■           °

здесь и j ( t ) - операторы используемых управляющих устройств (в данном случае интегральные)

l с заданными ядрами иj(t,т), определенными в треугольнике 0 < т < t < T, фj(т) = J 91 gjdx -0

воздействия на входе регуляторов, характеризующие состояние объекта управления и выражающиеся через весовые функции распределенного контроля g j (x).

Таким образом, задача оптимизации системы управления заключается в том, чтобы найти ,, такие весовые функции gj(x), при которых выходное значение функции состояния 9 1 (l, t) минимизировало бы функционал качества (4).

Лемма 1. Сопряженная система уравнений и необходимые условия оптимальности имеют вид ц"+ц(x,t .■-д(x,tM „(x,tк -

• - jf Ц.           (ti, t)gj (x Wi +

T'

• <    ц ^{( |} , ^ ⁽ l , , * о ⁽ t , t ** . ⁽ x ) = °;

• дЦ.(x,t) ц (x t)дЦ2(x,t) . (x t)k i ц (x t)k = °-

• [ 9^

• ц(x,T)= °) Ц^((x,Tц=V  ’   .(’ Ц^  ’

Tt

0,1,Ц'                       °(,11- lTt

Lj (91,ц ) = f f ц (^,t)Zj (^)f uj(t'T)9^(x'T)dTdtd^ = °.

0 0°

Метод решения системы уравнений заключается в следующем:

• а)    задаются начальные приближения весовых функций g ⁰ ( x ) ;

• б)    если g j ( x ) известны, то из системы уравнений (1) и граничных условий (2) и (3) находятся ⁹ n = 9 i ⁽ x , t ) и из сопряженной задачи ⁽6^)-(8) определяются ^ц = ^{ц (} x , t ) , i = 1, 2;

• в)    далее полагаем:

g 0 ⁺ 1 = g 0 - T L 0 ( ^ j , Ц ) , T >  0;

gf = g j - tl^ , ц ) , n = 0,1,2,...

• г)    предельные значения весовых функций дают решение задачи.

Для численной реализации задачи (1)–(3), (6)–(10) построена явная консервативная конечно-разностная схема, аппроксимирующая исходную систему уравнений (1) с первым порядком на равномерной сетке.

При этом справедлива

Лемма 2. Левые части конечно-разностных аналогов уравнений (9)-(10) представляют собой градиент аппроксимированного функционала качества (4).

Следовательно, для решения нашей задачи может быть использован градиентный метод. На рис. 1–7 приведены примеры расчета систем контроля по разработанной программе.

На рис. 1 а представлены кривая разгона, оптимальная переходная характеристика в одноконтурной схеме регулирования с весовой функцией оптимального контроля g ₀ (x). Эта функция отражена на рис. 1 б . На рис. 2-7 показаны кривые оптимального управления и соответствующие функции распределенного контроля с подачей управляющих воздействий в точках, распределенных по длине аппарата. Индекс «1» функции g i (x) соответствует координате x j = 0,1; «2» - x 2 = 0,2 и т.д. На рис. 7 управляющие воздействия подаются в пяти точках одновременно.

Результаты расчетов показывают также эффективность выбора дополнительного контура управления с подачей управляющего воздействия в промежуточные точки объекта с распределенными параметрами. С увеличением координаты x i качество распределенного контроля улучшается. Наибольшее улучшение соответствует точке с координатой x i = 0,5.

С увеличением x i этот эффект снижается. Таким образом, качество управления зависит как от распределенного контроля, так и от распределенного управления. Примерами расчетов для промышленных аппаратов доказана необходимость выбора промежуточных точек контроля за управляемым процессом и точек дополнительных управлений с целью повышения эффективности систем управления и проведения технологических процессов в соответствующих режимах объектов с распределенными параметрами.

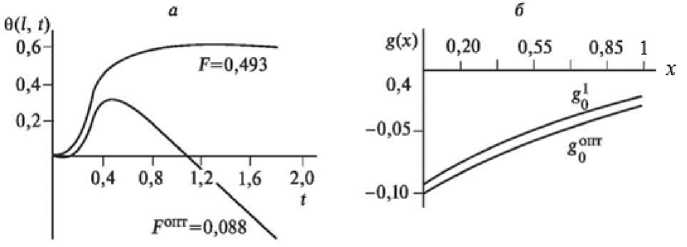
Рис. 1. Изменения температуры в переходном режиме и при оптимальном контроле (a) с весовой функцией g 0 (x) (б)

Fig. 1. Temperature changes in transient mode and at the optimal control (a) with the weight function g ₀ (б)

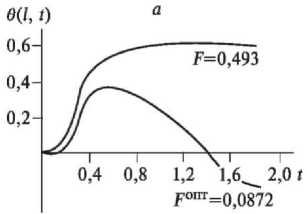
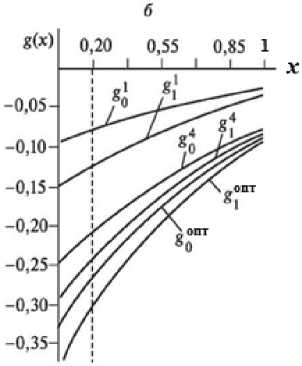
Рис. 2. Изменения температуры в переходном режиме и при оптимальном контроле (а) с весовыми функциями g 0 , g 1 (б)

Fig. 2. Temperature changes in transient mode and at the optimal control (a) with the weight functions g ₀ , g ₁ (б)

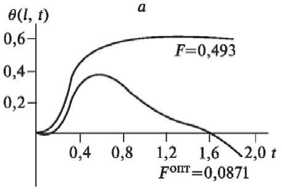
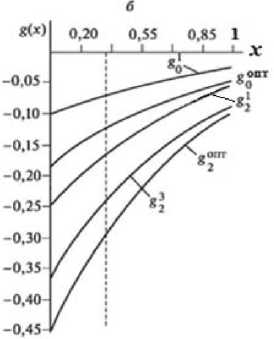
Рис. 3. Изменения температуры в переходном режиме и при оптимальном контроле (а) с весовыми функциями g 0 , g 2 (б)

Pic. 3. Temperature changes in transient mode and at the optimal control (a) with the weight functions g ₀ , g ₂ (б)

На практике распределенный контроль для ректификационных колонн сводится к выбору контрольных тарелок, а распределенное управление – к выбору тарелок питания и тарелок отбора боковых продуктов. При этом постановки соответствующих задач и выбор методов их решения могут быть разнообразными.

Рассмотренная нами задача достаточно легко обобщается на любое конечное число параметров, характеризующих управляемый процесс. Здесь получила дальнейшее развитие идея распределенного контроля и управления для повышения качества проектируемых и действующих систем управления. Идея распределенного контроля и управления естественным образом вытекает из нужд реальных систем. Однако при этом важной является математическая – 225 –

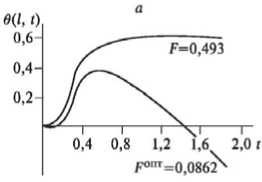
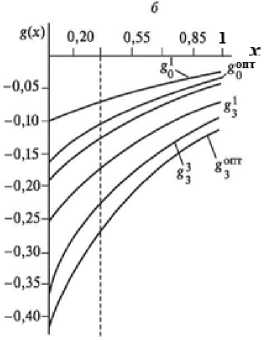
Рис. 4. Изменения температуры в переходном режиме и при оптимальном контроле (а) с весовыми функциями g 0 , g 3 (б)

Pic. 4. Temperature changes in transient mode and at the optimal control (a) with the weight functions g ₀ , g 3 (б)

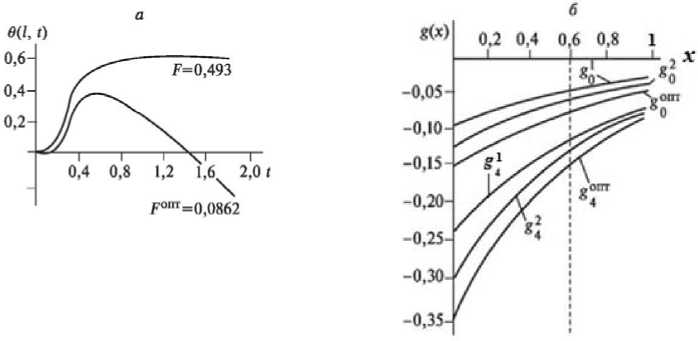
Рис. 5. Изменения температуры в переходном режиме и при оптимальном контроле (а) с весовыми функциями g 0 (x), g 4 (x) (б)

Pic. 5. Temperature changes in transient mode and at the optimal control (a) with the weight functions g ₀ (x), g ₄ (x) (б)

постановка задач с использованием распределенного контроля и управления. Для решения поставленных задач применяются численные методы. Получаемая функция распределенного контроля может быть использована при проектировании систем управления. После того как найдена оптимальная функция распределенного контроля ее можно аппроксимировать конечным числом точек, а сама непрерывная функция представляет собой предельную оценку и может быть также использована при синтезе распределенных систем оптимального управления.

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края, Красноярского краевого фон-

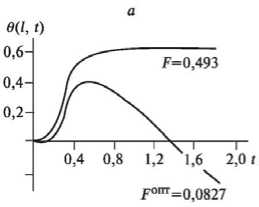
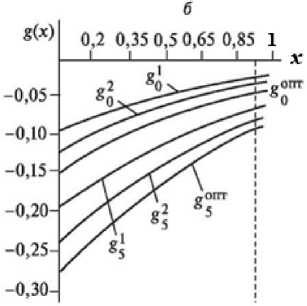
Рис. 6. Изменения температуры в переходном режиме и при оптимальном контроле (a) с весовыми функциями g 0 (x), g 5 (x) (б)

Pic. 6. Temperature changes in transient mode and at the optimal control (a) with the weight functions g ₀ (x), g ₅ (x) (б)

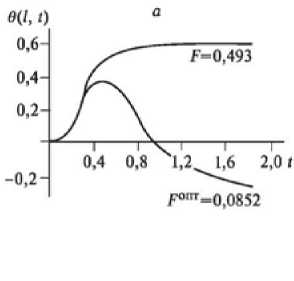
Рис. 7. Изменения температуры в переходном режиме и при оптимальном контроле (a) с весовыми функциями g 0 , g 1 , g 2 , g 3 , g 4 , g 5 (б)

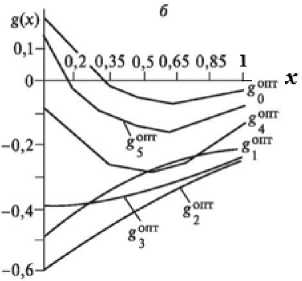
Pic. 7. Temperature changes in transient mode and at the optimal control (a) with the weight functions g ₀ , g ₁ , g₂, g ₃ , g ₄ , g ₅ (б)

да поддержки научной и научно-технической деятельности» в рамках научного проекта No 17-48-240386 р а.