Распределённая система идентификации статических моделей стохастических объектов

Теория управления вышла на уровень, обобщающий основные системные принципы, распространился кибернетический подход о единстве проистекающих процессов в естественных и искусственных системах. По этой причине возникла потребность установления аналогий описания этих систем для целенаправленного управления различными сферами деятельности. Это обусловило необходимость создания обобщённого подхода к моделированию и выделению отдельного направления теории автоматического управления, занимающегося идентификацией.

Показатели выходных величин реальных объектов подвержены искажению – показатель любого измерительного устройства включает не только истинное значение, но и помеху. Этот факт приводит к необходимости разработки устойчивых алгоритмов, учитывающих и устраняющих искажающие воздействия.

Поскольку любая задача моделирования предъявляет высокие требования к производительности вычислительной инфраструктуры, то неизбежно возникает необходимость выбора алгоритмов, оптимальных по быстродействию, а вместе с тем поднимается вопрос увеличения производительности. На сегодняшний день выделяются следующие эффективные методы повышения производительности:

• •    установка на материнскую плату компьютера многоядерного процессора или/и нескольких процессоров;

• •    вынесение части вычислений на видеокарты [4];

• •    построение суперкомпьютеров [2];

• •    объединение нескольких компьютеров в вычислительную сеть [7, 8].

Цель исследований . Разработка концепции распределённой вычислительной системы идентификации статических моделей.

Задачи исследований . Определение архитектуры системы, выделение составных частей (узлов) и их функционала, механизма взаимодействия между узлами и соответствующих программных алгоритмов для каждого из узлов.

Объекты исследований . Статические модели стохастических объектов [3], в том числе и объекты с многомерными входными воздействиями.

Результаты исследований и их обсуждение . Архитектура системы. Каждый узловой элемент предлагается определить как изолированную самостоятельную систему.

Наложим на систему требование к безотказной работе. Под этим следует понимать независимость конечного результата вычислений на стартовом узле, на котором в рассматриваемый момент времени пользователь инициализировал вычисления от любого другого элемента распределённой системы. Это неизбежно накладывает требование функциональной избыточности на каждом узле, что означает возможность проведения всех вычислений либо без участия других элементов сети (по непосредственному запросу пользователя), либо в случае их отказов. Это означает, что программное обеспечение каждого узла должно включать реализацию всех алгоритмов идентификации, которые предлагаются пользователю.

Отметим, что каждый узел относительно включаемых алгоритмов следует представлять как модульную систему. Каждый алгоритм, если он требует некую априорную информацию, конфигурируется администратором текущего узла.

Руководствуясь самодостаточностью каждого узла, можно утверждать, что пользователь абсолютно точно не получит результат вычислений только в случае отказа именно стартового узла. Если же происходит отказ на другом узле сети, то вычисления будут делегированы ближайшему узлу, успешно справившемуся с предыдущими задачами, либо будут произведены непосредственно на стартовом узле. Таким образом, переходим к рассмотрению механизмов взаимодействия между узлами.

Взаимодействие узлов. С точки зрения вычислительной сети топология данной концепции распределённой системы идентична топологии «звезда» [2]. Каждый узел сети предлагается конфигурировать, задавая IP-адреса возможных участников вычислений. Возможный вариант составных частей системы представлен на рисунке.

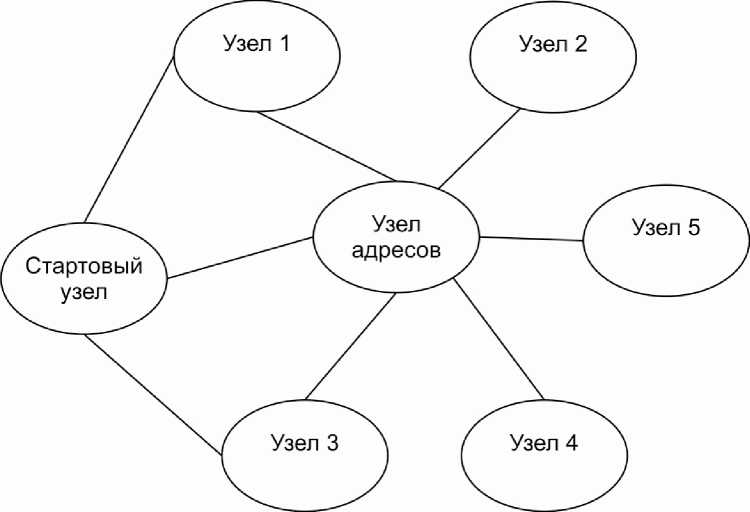
Пример конфигурации сети

По представленной конфигурации определим роли каждого узла и основные особенности сети:

• •    стартовый узел. На этом компьютере пользователь непосредственно запускает вычисления, отсылая узлам 1, 3 и узлу адресов выборку измерений объекта. В случае отказа или таймаута одного из узлов, адресному узлу отправляется сообщение с указанием требуемых алгоритмов. В случае отказа адресного узла, оставшиеся алгоритмы выполняются непосредственно на стартовом узле, о чём пользователь уведомляется;

• •    узлы 1 и 3 участвуют непосредственно в данном процессе вычислений. Получив данные и указания от стартового узла, и затем, выполнив вычисления, результат отсылается обратно стартовому узлу;

• •    узел адресов ожидает исходной выборки объекта и при получении от стартового узла сообщения о необходимости проведения вычислений осуществляет распределение нагрузки между своими ресурсами и

• узлами 2, 4, 5. Важно отметить, что конфигурация стартового узла может содержать как 0 адресных узлов, так и больше одного.

Реализация. Опишем уже существующие программные реализации важных алгоритмов идентификации, которые предлагается включить в изначальную версию системы.

Рассмотрим работу подпрограммы построения непараметрической оценки регрессии. На первом этапе программа получает выборку входных измерений. В случае возникновения ошибки пользователю выводится соответствующее уведомление, и программа завершается.

Далее минимизируется критерий “скользящего экзамена”:

1nn

In =-S (yi — ПпЫ)2 = min , VnM = 2 ШкМУк ,(1)

n i =1

k ^ i где ик (xj - вес k-й точки, вычисляемый по следующей формуле:

®кМ =

m

П к( в

j = 1

X ■ — X, .

ij     kj

^Xj

nm

2П ^к ( в , l = 1   j = 1

X j- X j- ^Xj

)

0 .75( 1 - z ² ), |z| < 1

0 ,                1 < |z| .

Экстремумом функции (1) являются оптимальные значения коэффициентов размытости в • Вычисление функции скользящего экзамена происходит равномерно в нескольких потоках, в том числе и в главном. Для реализации многопоточных вычислений используется стандартная библиотека thread языка C++11.

На последнем этапе измеряется выход полученной оценки при входных воздействиях, аналогичных выборке экспериментальных данных. Полученные значения записываются в лог.

Переходим к рассмотрению алгоритма построения параметрической модели. В общем случае модель имеет следующий вид:

^

Y = а ₀ + ф ( а ,Х) ,                                 (3)

где ф ( а ,Х) - функция, зависящая от входных воздействий X и от параметров модели ^а . Если модель линейна относительно своих параметров, то она преобразуется в следующую формулу:

m

Y = а + 2 ^а j^^(x) ,                            ⁽⁴⁾

i = 1

где ^ (X) - заданная пользователем базисная функция, зависящая от входа X;

а₀,а - параметры модели. Их оценки находятся из решения системы линейных алгебраических уравнений, получаемой из критерия минимума среднего квадратичного отклонения:

M{Y - Y} = о , M ^!

ФОХ)- (Y _р) а

* = 0 ,j = 1 ,m

На первом этапе работы программы происходит синтаксический анализ конфигурационного файла, содержащего базисные функции. В результате синтезируются объекты-функторы, представляющие собой лямбда-выражения языка C++11. Для разработки двухступенчатого парсера использовались программы Lex и Bison – генераторы лексических и синтаксических анализаторов соответственно [9].

Следующим этапом служит составление системы линейных алгебраических уравнений согласно критерию наименьших квадратов и полученной выборки измерений с последующим её решением, в результате чего вычисляются оценки параметров линейной модели.

На последнем шаге программа измеряет выход составленной параметрической модели при тех же входных воздействиях, что и в исходной выборке измерений. Результаты записываются в лог.

Заключение . Предложена концепция распределённой вычислительной системы, в которой узлы эквивалентны относительно функционала требуемого на момент запуска пользовательских вычислений, и концепция взаимодействия между узлами, для каждого из которых обозначены роли и принципы их функционирования. Описаны уже существующие реализации алгоритмов, предлагаемых к включению в изначальную версию программного комплекса. Дальнейшее развитие проекта видится следующим: разработка программных реализаций уже существующих алгоритмов для видеокарт [1] и кластерных систем [5]; разработка и апробирование алгоритма непараметрической идентификации для объекта с многомерным входом; обеспечение сетевого взаимодействия между узлами. Предлагается использовать генератор серверных спецификаций Apache Thrift [6], а также разработку соответствующих приложений для известных мобильных устройств с целью их возможного включения в программный комплекс.