Распространение нестационарных антисимметричных кинематических возмущений от сферической полости в среде Коссера

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2020PNRPU MECHANICS BULLETIN

C развитием современной науки и техники требуется точное знание процессов деформирования материалов с усложненной структурой. Этому требованию отвечают модели упругих моментных сред, к которым, в том числе, относится модель Коссера. Общая теория такой несимметричной теории упругости впервые была разработана братьями Коссера (Э. и Ф. Коссера) [1].

В настоящий момент моментная теория упругости привлекает внимание многих исследователей. В [2] рассмотрена динамическая связанная осесимметричная задача микрополярной теории термоупругости для изотропных слоя, полупространства или пространства. А в работах [3–5] получены решения аналогичных нестационарных осесимметричных задач для однородной изотропной среды псевдокоссера. В статьях [6,7] построены решения двумерных нестационарных задач для упругих моментных полупространств и полуплоскости. В работах [8, 9] исследованы осесимметричные задачи для упругих тел со сферическими границами. В [10, 11] исследованы особенности распространения плоских периодических и уединенных волн. B работе [12] рассматривается задача о распространении поверхностных волн в среде Коссера (случай полупространства), в [13] исследовано распро-странене нестационарных поверхностных возмущений для полуплоскости, заполненной псевдоконтинуумом Коссера. Континуальная модель слоистой среды изучалась Н.В. Зволинским и К.Н. Шхинек в работе [14].

В статье [15] рассматривается начально-краевая задача для тонкой пластинки с позиций общей трехмерной несимметричной теории упругости. В статье [16] исследуется динамическая задача для микрополярных упругих тел при помощи использования метода собственных значений. В [17] рассматривается динамическая связанная осесимметричная задача микрополярной теории упругости для бесконечной в радиальном направлении изотропной среды. В статье [18] получен ряд новых аналитических решений статических и динамических волновых задач линейной упругой среды Коссера. В цикле работ М.А. Кулеша рассматриваются задачи о распространении объемных продольных и поперечных волн [19]. В статье [20] изучаются одномерные динамические уравнения микрополярных упругих тонких балок со свободным вращением, со стесненным вращением и «малой сдвиговой жесткостью». В том числе рассматриваются свободные колебания балок при шарнирном опирании на концах. В статье [21] динамическая задача моментной теории упругости о трещине конечной длины при нормальной нагрузке на берегах методом интегральных преобразований сводится к системе сингулярных интегральных уравнений относительно пе- ремещений и поворотов, которая решается численно. Нелинейные моментные теории упругости рассматриваются в работах [22–26]. В статье [27] рассматриваются поверхностные волны в упругом слоистом полупространстве с периодическим изменением жесткости по глубине.

Целью работы является постановка задач о распространении нестационарных антисимметричных кинематических возмущений от сферической полости в среде Коссера.

1. Постановка задачи

Полагаем, что в начальный момент времени t = 0

возмущения отсутствуют:

∂ u u t =0 = 0, _{∂ t}

=0,Φ

=0, ∂∂Φt

= 0,

Ψ= 0, ^∂Ψ t =0      , _∂ t

= 0,

t =0

Рассмотрим однородное изотропное упругое моментное пространство со сферической полостью радиусом R , занятое средой Коссера [28]. Используем сферическую систему координат r , θϑ где r ≥ 0,0 ≤θ≤π , 0 ≤ϑ< 2 π , с началом в центре полости и оронормиро-ванным базисом e r , e _θ , e _ϑ .

Полагаем, что движение является аналогом рассматриваемой в теории упругости антиплоской деформации – антисимметричным относительно полупрямой θ= 0 , что соответствует следующим полям перемещений u и вращения ω :

u = u ( r , θ , t ) e _ϑ , ω =ω r ( r , θ , t ) e r +ω_θ ( r , θ , t ) e _θ , Ψ =Ψ ( r , θ , t ) e ϑ , Φ=Φ ( r , θ , t ) .

При этом координаты вектора ω связаны со скалярным Φ и векторным Ψ =Ψ ( r , θ , t ) e _ϑ потенциалами следующим образом:

∂Φ 1∂ 1∂Φ 1∂(rΨ)ωr = + (Ψsinθ), ωθ = - . (1) ∂r rsin θ ∂θ r∂θ r∂r

а на границе полости заданы кинематические возмущения

ur=1=U0(θ,τ),ωrr=1=Ωr0(θ,τ),ωθr=1=Ωθ0(θ,τ). (4)

Решение начально-краевой задачи (1)–(4) разыскивается в классе ограниченных функций.

Выражения для компонент тензоров напряжений и моментных напряжений в силу громоздкости здесь не приводятся, и далее ограничимся нахождением только кинематических параметров среды.

Отметим, что частный случай граничных условий (4) соответствует жестко сцепленному с полостью единичного радиуса абсолютно твердому шару, поворачивающемуся вокруг оси θ= 0 по закону Ω ( τ ) . Действительно, при этом вектор поворота Ω и правые части последних двух равенств в (4) имеют вид:

Ω =Ω ( cos θ e r - sin θ e _θ ) , Ω _{r 0} =Ω cos θ , Ω_{θ 0} ( θ , τ ) =-Ω sin θ .

Такое движение среды описывается тремя уравнениями [28]:

Вектор перемещения поверхности шара U и правая часть первого равенства в (4) определяются так:

U =Ω sin θ e _ϑ , U ₀ =Ω sin θ .

Далее везде будем использовать безразмерные величины (при одинаковом начертании они обозначены штрихами, которые в последующем изложении опущены):

где

^{∂ 2 u} 2 = c 2 ² α D ( u ) - ^{2 α} D ( Ψ ) , ∂ t ρ

c42ΔΦ-4αΦ,∂Ψ2=c32D(Ψ)+2α(u-2Ψ), J∂tJ

′

r , τ= c ¹ t , u ′= u , U ′= U ⁰ , Φ′= ^Φ ,

RRR ⁰ R L

Ψ        c ² c ² c ²

Ψ′ = , γ 02 = 1 2 , γ 12 = 1 2 , γ 22 = 12 ,

L        c ₄ c ₂ c ₃

λ+2μ      α     ρL2

c1=,α′=,υ=,η1+α =γ12+α, ρ          ρc12        J

D ( u ) =Δ u - ^u ,Δϕ=¹ r ²sin²θ         r ²

c =^μ c = ^γ+ε c = ^{β+ 2 γ} c ²= c ²+ ^α c 2 =_ρ, c 3 = _J , c 4 = _J , c 2 α = c 2 +_ρ

Здесь t – время; μρ и J - упругая постоянная Ламе, плотность и мера инерции среды при вращении (плотность момента инерции); α , β , γ , ε - физические параметры континуума Коссера, характеризующие наличие моментных эффектов; c ₂, c ₃ , c ₄ и c _{2 α} – скорости распространения волн; Δ – оператор Лапласа для скалярной функции.

где λ – упругая постоянная Ламе; c ₁ – скорость распространения волн растяжения-сжатия.

В этих величинах кинематические соотношения (1) и граничные условия (4) сохраняют свой вид, а уравнения (2) и начальные условия (3) записываются следующим образом (точками здесь и далее обозначены производные по безразмерному времени τ ):

Ф = Y-2 АФ- 4аиФ,

0                                      (5)

м=п+аD(u)-2aD(Т), T = y-2D(Т) + 2аи(u-2Т).

u\ п= г^1 „ =^Ф1 „=ф| =Т =т| = 0. (6) τ= 0 τ= 0 τ= 0 _τ= 0        τ= 0        _τ= 0

2. Представление решения в виде рядов

L rnlr=1

= ^{to L} 0 n ( ^s )( n >  0 ) , u nL I ,= ^UL ( ^s ) , r =1

Потенциалы, перемещения и координаты вектора вращения представляем в виде рядов по полиномам

Лежандра P n ( x ) и Гегенбауэра С - ( x ) [30]:

^to Ln|r =1

= ^to L 0 n ( ^s ) ( n >  ¹.

где

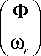
м

=z n=0

to rn

P n ( cos 6 ) ,

^to Ln

дФ L д r

T L n (n +1) —- (n > 0).

' u ^

T

, to J

м sin 6Z n=1

f _T 1

n

I to n J

to

L _Ф L 1 ^{д( r T} L )

C - ( cos e ) .

’ e n

r

r д r

Подставляя их в (1), получаем

дФ ,    , T , torn = ^-n(n +1) — (n > 0). д r            r

toe n

Ф- 1 ^ I r T n l ( n >  1 ) r r д r

Общее решение уравнения (11) имеет вид [31–33]

Ф L = ]Z C ( 0 ’ ( s ) Z n ( ^ 0 r ) . X 0 = Y 0 V s ² + 4au ( ReX 0 > 0 ) .

'=1           1                                 1                        (15)

Z (_z ) =     к    (z ). z (z ) = I    (z ).

1 n \ /             n+12 \ /. 2n\)            n+1/2 \ / zz

При этом уравнения (5) и условия (4), (6) переходят в следующие равенства:

^Ф n = Y 02 A n ^Ф n ^- 4 аиФ n ( n >  0 ) .

Un =CAnUn - 2aAnTn.(8)

T n = Y - ² A n T n + 2 au ( U n - 2 T n )( n >  1 ) .

toД=1 to r 0 n (T) ( n > 0) . un\r=1 = U 0 n (T) .(9)

to n l r =1 ^to e n ( ^T ) ( ⁿ >  ¹ ) .

^Ф n L= 0 ^Ф . L = ⁰ ( n >  0 ) . U n L. =

= U■ 1=0 =T n L=0 T n l,,0 = 0 (n > 1) -(

Здесь с . 0 ’ - постоянные интегрирования; I v ( z ) и K v ( z ) - модифицированные функции Бесселя первого и второго рода порядка v .

Для построения общего решения системы из второго и третьего уравнений (12) используем достаточно просто доказываемое утверждение .

Пусть матрица системы обыкновенных дифференциальных уравнений

Здесь использованы разложения в ряды правых частей условий (4):

м

^U 0 ( ^e , ^T ) = ^- sin ^e Z u 0 n ( ^T ) C ³ - ² ( cos ⁶ ) .

n =1

м

^Q r 0 ( ⁶ , ^T ) Z ^to r 0 n ( ^T ) ^P n ( cos ⁶ ) .

n =0

м

^ e ( ⁶ , ^T ) = ^- sin ⁶ Z ^to 60 n ( ^T ) О ( cos ⁶ ) .

n =1

Соотношения (7)–(10) при каждом n вместе с требованием ограниченности образуют независимые начально-краевые задачи.

m

L ( У ) = Ay . L ( У ) = Z b m - k ( ^x ) У ⁽ k ’ ( ^x ) .

k =0                              (16)

У = ( У 1 ( ^x ) . У 2 ( ^x ) ..... у . ( ^x ) ) T . A = ( a ij ) _{n x n} ( ^x . a j е К ) .

где a_ij не зависит от x , имеет простой спектр с собственными значениями Z k и собственными векторами Y _k ( k = 1,2..... n ) . Тогда ее общее решение имеет вид

y = Tz . т = ( Y 1 ..... y . ) .

Tm z = ( z1 ( x) . z 2 ( x ) ..... zn ( x )) . zk = Z CklFkl ( x ).

I =1

3. Изображения общего решения

Для решения этих задач применяем к ним преобразование Лапласа по времени ( S – параметр; индекс « L » обозначает трансформанту). В результате получаем краевые задачи относительно изображений:

где { F ki ( ^x ) } ( I = ¹.²..... m ) - фудаментальные системы решений уравнений L ( z_k ) =Z _kz_k . а C_kl - произвольные постоянные.

В свете этого утверждения систему уравнений записываем в матричном виде

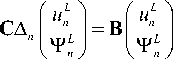
s ² Ф L = y - ² A n Ф L - 4 аиФ L ( n >  0 ) .        (11)

B =

5 ² U L n ' A U - 2 aA n T L .

s ² T L = 2 au u L + ( y - ² A _n - 4 au ) T L ( n >  1 ) .

f s ²           0 1

- 2 au ( s ² + 4 au )

( T!+

C — ⁿ 1a

. I 0

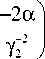
и приводим ее к канонической форме (16):

I w I I w I u_nu_n n | W L I      | W L I ,

V n / V n /

A = C ^{- 1} B = -' 2-

'-2 s 2

4 a ² u )

, +

- 2 aun 1

11a

2 a ( s ² + 4 au )

<( s2 + 4au) ?

Здесь использованы обозначения

X in ( z ) = Z' n ( z ) = ¹ Г n^Z ln ( z ) ⁺ ( ^{- 1} ) ¹ z ^Z l, n +1 ( z ) ! ,

₁ ^z                               (19)

Y in ⁽ z ) =      Z in ⁽ z ) , ^Y + 2, n ⁽ z ) = Y in ⁽ z ^)- X in ⁽ z ) .

z

Далее строим характеристическое уравнение матрицы A относительно собственных значений X ². Как оказывается, оно сопадает с аналогичным уравнением для осесимметричной задачи [30], и его корни определяются так:

₂ B 0 + a B 1 ± ^D₀ - 2 a D 1 + a ² D ₂

^1,2 =           2^! 7OY 21           ,

B o = ( Y 2 + Y 2 ) s 2 , B i = Y 2 ( Y 2 s ² + 4 u ) , D o = ( Y 2 -y 2 ) 2 s 4 , D = Y 2 ( Y 2 -Y 2 ) s ² ( Y 2 s ² + 4 u ) ,

D 2 =Y 2 [y 2 ( Y 2 s ² + 4 u ) 2 - 16 uY 4 s ² ] .

Соответствующие X 2 собственные векторы есть решения систем линейных алгебраических уравнений

( A -X k E ) Y k = 0 , Y k = ( y ik , y 2 k ) T .

Их выбираем так, чтобы имела место линейная независимость и при a = 0:

У 11 =y 2 ( s ² + 4 au ) -X 2 , y 21 = 2 aY 2 u ,

У 12 =- 2 aY 2 y 2 ( s ² + 4 au ) ,             (17)

У 22 = Y 2 ( s ² - 4 a ² Y 2 u ) - X 2 ( 1 + aY 2 ) .

Следовательно, в соответствии с (16) общее решение системы уравнений (12) имеет вид

I u ^L        2 ( y A _{z x}

I A L = ER * 1 C- ’ ( s ) Z- ( ^X k r ) -

V W - J k , I =1V y 2 k )

Далее, подставляя (15) в (14), с учетом свойств функций Бесселя получаем следующие результаты:

to Ln =X0 E C- 0)( s) Xin (X0 r) + l=1

+n (n+1) E y 2 kCnk)(s )X kYin (X kr), k, i=1

to Ln =-X 0 E C - 0 ) ( s ) Y n ( X 0 r ) +            (18)

i =1

+ E У2kXkC-k)(s)Yi+2,n (Xkr), k, i=1

u ^L = E У 1 k C n^k ) ( ^s ) Z in ( ^X k ^r ) .

• k , i =1

• 4.    Изображения решения задачи

Поскольку функция Бесселя In+1/2 (z) неограничена в окрестности бесконечно удаленной точки [30], то в силу (15) и (19) таковыми же являются и функции Z2n (z), X2n (z), Y2n (z). Следовательно, в (18) необхо- димо положить C-^2)(s) = 0 (j = 0,1,2). Подставляя теперь с учетом этого равенства (18) в (13), получаем алгебраические уравнения относительно постоянных интегрирования:

^sC 00 ) ( ^s ) X 10 ( ^s ) = w Lo ( ^s ) .

A n C n = B n (n > 1), n ( n + 1) У21X1 Yn (X1) n (n +1) У22X2Yn (X2 )1 (20)

A n = -X 0 Y n ( X 0 )

V ⁰

У 21 ^X 1 ^Y 3 n (^X 1 )

У 11 ^Z 1 n (^X 1 ) C n 0 ’ ( s ) I

to ,

У 22 ^X 2 ^Y 3 n (^X 2 )

y 12 ^Z 1 n ^(X 2 )      _?

( X 0 ) I

,

= C n 1 ’ ( s ) , B n = to L 0 n ( X o ) .

C - ( s )

u - ( X 0 )

Подставляя их решения в (14), получаем изображения искомых функций:

^to Ln ( r , ^s ) = G to Lrrn ( r , ^s ) ^{to L} 0 n ( ^s ) ⁺

+ Gtoren ( r, s )to00 n ( s ) + Gtorun ( r, s ) u0 n ( s ) , toen(r,s) = Gtoern(r,s)tor 0 n(s)+

+ Gtoeen(r,s )toe0n(s) + Gtoeun(r,s)u0n(s), uL ( r, s ) = GLtorn ( r, s )toL0n ( s ) +

⁺ G u toe n ^{( r} , ^s ) ^to e0 n ^{( s} ) ⁺ G u to un ^{( r} , ^s ) ^u 0 n ^{( s} ) .

Здесь G to Lrrn ( ^r , ^s ) ,^, G uL to un ( ^r , ^s ) ^- изображения ^поверхностных функций влияния, которые определяются так:

DnGtoLrrn =X0 X1 n (X0 r ) An 11 + n ( n + 1) E У2 k X kY1 n (X kr ) An 1, k +1, k =1

DnGtoren = X0 X1 n (X0 r ) An 21 + n ( n + 1) E У2 k X kY1 n (X kr ) An 2, k+1, k =1

_L 2

n to run        0 1 n \ 0 / n 31       \        ) / iУ 2 k k 1 n \ k / n 3, k+1, k =1

DnGtoe rn = -X0 Y1 n (X0 r ) An 11 + E У 2 k X kY3 n (X kr ) An 1, k+1, k =1

DnGtoeen = -X0 Y1 n (X0 r ) An 21 + E У2 k X kY3 n (X kr ) An 2, k+1, k =1

^Dn^G «0 un = ^-* 0 Y n ⁽* 0 r ) ^An 31 ⁺ Z y 2 k * k Y 3 n ⁽* k r ) A n 3, k + 1 ,          ⁽²¹⁾

k = 1

DPIrn = Z У1kAn 1,k+1Z1 n (*kr), k=1

DnGu «0 n = Z y1 kAn 2, k+1Z1 n (* kr ) , k=1

Dn (s) GLun (r, s) = Z y1 kAn3,k+1Z1 n (*kr) , k=1

D n ( s ) = |A n | = * 0 [ X 1 n ( * 0 ) A n 11 ( s ) - Y n ( * 0 ) A n 21 ( s ) ] .

В этих равенствах и далее A_nij ( s ) - алгебраическое дополнение расположенного в i-й строке и j -м столбце элемента матрицы A _n .

• 5.    Линейное приближение решения

Получить аналитически оригиналы функций влияния при n >  1 не представляется возможным. Поэтому используем разложения в степенные ряды по малому параметру а , ограничиваясь только линейными слагаемыми. При этом приближенные равенства заменяем точными.

Соответствующие равенства для * _{0 1 2} и координат (17) собственных векторов имеют вид:

. Г 2аи) .* =70, s +----- I, *1 =Y1as, k s )

. Г . 2 au)             г,------

• * 2 Y ; s ⁺ I , У , Y \' ^-a Y .

k s )

У н = (^ -7 2 ) s ² + a ( 7 4 s ² + 4 VT 2 ) , У 21 = 2 а^и , у 22 = ( Y 2 -7 2 ) s ² -а^ ( Y ² s ² + 4 u ) , У 12 2 ал ' Y 2 s ².

где

H1 ^L ( r , s ) =	- n ( n + 1 )Y 2 к « Fl\(r , s ) ( k = 0 2) Y 1 r n + 2 s 2 P n ( Y 0 s , Y 2 s ) R n 0 ( Y 1 s )         , ,
Hin ( r , s ) =	y 2 k « F «0 un ( r , s ) -------( , = 0 12) Y 1 r n + s P n ( Y 0 s , Y 2 s ) R n 0 ( Y 1 s )
Hl nL ( r , s ) =	'Y.'Y.^ F (1 k ) Y 1 n « и « rn --------( k = 12) _ r" +P„ ( Y 0 s , Y 2 s ) R n 0 ( Y 1 s )
Hl n ( r , s ) =	Y 1 Y 2 k « F L0 n       ( k = 1 2 ) k = 2 Wk r" +1 P n ( Y 0 s , Y 2 s ) R n 0 ( Y 1 s )            , « Y 2 -Y 2

F2 ( ^r , ^s ) = [ R n 0 ( Y 1 ^s ) R n 3 ( Y 2 ^s ) ^-- R n 3 ( Y 1 s ) R n 0 ( Y 2 s ) ] R n 1 ( Y 0 rs ) , F un ( ^r , ^s ) = ^P n ( Y 0 ^s , Y 1 s ) R n 0 ( Y 2 ^rs ) , ^1 ( r , s ) = n ( n ^{+ 1} ) ^R n 0 ( Y 0 rs ) ^{X X} [ ^R n 3 ( Y 1 s ) R n 0 ( Y 2 s ) ^- R n 0 ( Y 1 s ) R n 3 ( Y 2 s ) ] , F* n ( ^r , ^s ) = R n 3 ( Y 1 ^rs ) ^P n ( Y 0 ^s , Y 2 ^s ) , F2n ( ^r , ^s ) = ^- R n 3 ( Y 2 rs ) ^P n ( Y 0 s , Y 1 s ) , F u L rn ( r , s ) = ^R n 0 ( Y 2 s ) ^R n 0 ( Y 1 rs ) R n 0 ( Y 0 s ) , F u^n ( r , s ) = ^{- R} n 0 ( Y 1 s ) R n 0 ( Y 2 rs ) ^R n 0 ( Y 0 s ) , ^{F 1}1 ( r , s ) = R n 0 ( Y 2 s ) R n 0 ( Y 1 rs ) R n 1 ( Y 0 s ) , Il ( r , s ) = ^{- R} n 0 ( Y 1 s ) R n 0 ( Y 2 rs ) ^R n 1 ( Y 0 s ) .

G Ln ( r , s ) = G Z ⁰ ) ^L ( r , s ) ^+a G z n ) ^L ( r , s ) ,

G Z n*^L ( r , s ) = Z H Z n^k ) L ( r , s ) e ^-Y k ^{( r - 1 ) s}           (24)

k =0,2

(Z = torr, tor0, «0r, «00; l = 0,1).

Отсюда с учетом (20) следует, что имеют место следующие асимптотические соотношения:

У 12 , у 21 , A n 12 , A n 22 , A n 31 , A n 33 = ^O ( « ) , ^a ^ ⁰ ■

где

_r (0 k ) L ^{Z n}

(r,s ) = -

F Z ( 0 ^k ) ( r , s ) r ^{n + 2} P n ( Y 0 s , 7 2 s )

Их использование с учетом связи модифицированных функций Бесселя полуцелого индекса с элементарными функциями [30] позволяет с принятой точностью привести равенства (21) к следующему виду:

GL un ( r , s ) = H »un ( r , s ) e ^{-Y 1 a(} r ^{- 1 )}

H1 ) L ( r , s )

^{2 u} FF nk ) ( ^r , ^s ) r ^{n + 2} s ² P n ² (Y 0 s , Y 2 s ) ,

F ^ Z n k ) ( ^r , ^s ) = F Z ⁽ n k ) ( ^r , ^s ) ^P n ( Y 0 ^s , Y 2 ^s ) ^{+ + F} Z n°k ) ( r , s ) ^P n ^<1)( 7 0 s , Y 2 s ) .

H L un ^{( r} , ^s ) =

R n 0 ( Y 1« ^rs ) r n ^{+ 1} R n 0 ( Y 1a s ) .

Gi n ( r , s ) = a Z H 11 ( r , s ) e ^-Y k ⁽ r"^1V k =0,2

GL0un (r, s ) = aZ H0,  (r, s) e-Yk(r-1)s k=0

GL„ ( r , s ) = a Z H (2 ( r , s ) e k ^{( r - 1 ) s} k =1

GL ₆ n ( r , s ) = a Z Hl ( r , s ) e ~^Y k ^{( r - 1 ) s} k =1

F 1 ^{00 (} r , s ) = ^{- R} n 1 ( Y 0 sr ) ^R n 3 ( Y 2 s ) , F 1 ^{02 (} r , s ) = n ( n ^{+ 1} ) ^R n 0 ( Y 2 sr ) ^R n 0 ( Y 0 s ) , F 1 1 ⁽ r , s ) = - n ( n ^{+ 1} ) ^R n 1 ( Y 0 sr ) ^R n 0 ( Y 2 s ) , F 1 r to ⁽ r , ^s ) = n ( n ^{+ 1} ) ^R n 0 ( Y 2 ^sr ) ^R n 1 ( Y 0 s ) , F 10™ ⁽ r , s ) = ^R n 0 ( Y 0 sr ) ^R n 3 ( Y 2 s ) , F 10™ ⁽ r , s ) = - ^R n 0 ( Y 0 s ) ^R n 3 ( Y 2 sr ) , F l*. n, ⁽ r , s ) = n ( n ^{+ 1} ) ^R n 0 ( Y 2 s ) ^R n 0 ( Y 0 sr ) , F 100 n ⁽ r , s ) = - ^R n 1 ( Y 0 s ) ^R n 3 ( Y 2 sr ) ,

F to^ ⁽ r ^, s ) = R n 1 ( Y o sr ) ^R n 6 ( Y 2 s ) ⁺ R n 2 ( Y o sr ) ^R n 3 ( 7 ; s ) ^,

F^ ⁽r^, s ) = - n ( n ⁺ 1 ) [ ^R n 0 ( Y 2 sr ) ^R n 5 ( Y o s ) ^{+ R} n 0 ( Y o s ) ^R n 5 ( Y 2 sr ) ] ^{, F1} 6 n ⁽ r^, s ) = n ( n ⁺ 1 ) [ ^R n 0 ( Y 2 s ) R n 2 ( Y o sr ) ^{+ R} n 1 ( Y o sr ) ^R n 5 ( Y 2 s ) ] ^{, F1} 6 n ⁽ r^, s ) = - n ( n ⁺ 1 ) [ ^R n o ( Y 2 rs ) ^R n 2 ( Y o s ) ^{+ R} n 1 ( Y o s ) ^R n 5 ( Y 2 rs )^{] ,} F^ ⁽ r ^, s ) = - ^R n o ( Y o rs ) ^R n 6 ( Y 2 s )^- R n 3 ( Y 2 s ) R n 5 ( Y o rs ) ^,

F ^ ⁽ r ^, s ) = R n 3 ( Y 2 rs ) R n 5 ( Y o s ) ^{+ R} n o ( Y o s ) ^R n 6 ( Y 2 rs ) ^,

F^ n ⁽ r ^, s ) = - n ( n ⁺ 1 ) [ R n o ( Y 2 s ) ^R n 5 ( Y o rs ) ^{+ R} n o ( Y o rs ) ^R n 5 ( Y 2 s ) ] ^, F^ n ⁽ r ^, s ) = ^R n 1 ( Y o s ) ^R n 6 ( Y 2 rs ) ^{+ R} n 2 ( Y o s ) ^R n 3 ( Y 2 sr ) .

Здесь использованы следующие многочлены [33]:

R (_z\ ₌ V; _z n - k _{A =} ⁽ n ^{+ k ) !}

^{n o (} ) ^ ^nk , ^nk 2 ^k ( n - k ) ! k !^,

R n 1 ( ^Z ) = R n +1,o ( ^Z ) ^- n^R n o ( ^Z ) ^,

R n 2 ( z ) = R n 4 ( z ) + R n 1 ( z ) , R n 3 ( z ) = R n 1 ( Z ) — R n o ( Z ) ,

Rn 4 ( Z ) = Rn 1 ( Z ) + Rn o ( Z ) ,

R n 5 ( Z ) = R n 1 ( Z ) + R n o ( Z ) , R n 6 ( Z ) = R n 4 ( Z ) — R n o ( Z ) ,

^P n ( x ^, У ) = ^R n 1 ( x ) ^R n 3 ( У ) — n ⁽ n ⁺ 1) ^R n o ( x ) ^R n o ( У ) ^,

Pn(1)( x, У ) = Rn 2 ( x ) Rn 3 ( У ) +

^{+ R} n 1 ( x ) ^R n 6 ( У ) ^- n ⁽ n ⁺ 1) [ ^R n 5 ( x ) ^R n o ( У ) ^{+ R} n o ( x ) ^R n 5 ( У ) ] .

• 6.    Оригиналы решения

Из (22)–(24) следует, что коэффициенты перед экспонентами в изображениях функций влияния являются рациональными функциями параметра s . Анализ степеней числителей и знаменателей показывает, что среди этих функций только три неправильные дроби H L _{m un} , Н щ ГL и H (^L . Выделение у них целых частей приводит к таким результатам:

H Lun ( r , s ) = r ^{- 1} + H L _m unr ( r , s ) ,

H ( rrnL ( r , s ) = r ^{- 1} + H (^L ( r , s ) ,           (25)

H ^{(o2) L}(r s TY^{(o2) L} U 5'I

H m66 n ⁽ r , s ) r ⁺ H m66 nr ⁽ r , s ) ,

Здесь функции с дополнительным индесом « r » – правильные дроби. Их оригиналы так же, как и оригиналы остальных коэффициентов перед экспонентами, достаточно просто находятся с помощью вычетов. При этом обращение преобразования Лапласа для функций в (25) приводит к следующим равенствам [29, 34]:

Hu«un (r, T) = r-15(t) + Humunr (r, T) ,

H^(r,t) = r-15(t) + HWr (r,t) ,H2n (r,t) = r-15(t) + H^^2nr (r,t), где 5(t) - дельта-функция Дирака.

Окончательно оригиналы функций влияния в (23)– (25) в соответствии со свойствами преобразования Лапласа имеют следующий вид ( H ( т ) - единичная функция Хевисайда):

Gumun ( r, Т) = r-18 [Т-Y1a ( r - 1)] + Gumunr (r,т),

G u ™ unr ( ^r , ^t ) = H u ™ unr [ ^r , ^T- Y 1a ( ^{r -} 1 ) ] ^H [ ^t- Y 1 « ( ^{r -} 1 ) ] .

Gzn (r,t) = a ^ HZnk) [r,t-Yk (r- 1)]H[t-Yk (r- 1)] k =o,2

(z = toru, to 0u, u tor, u to 6) ,

Gzn (r, t) = Gzn* (r, т) + аGen’ (r, t) (Z = torr, tor6, to6r, to66), где

Gtol ( r, T) = r-15 [т-Yo ( r - 1)] + Gtorrnr ( r, T) ,

Gto^n ( r, T) = r-1 8 [T- Y2 ( r - 1) ] + Gtoeenr ( r, T) ,

Gtolr (r,t) = Htor™r [r,т- Yo (r- 1)]H [r,t- Yo (r - 1)] + + H^rn [r, T-Y2 ( r - 1)] H [r, T-Y2 ( r - 1)] ,

Getonr (r, t) = Hto^n [r, t- Yo (r - 1)] H [r, t- Yo (r - 1)] + + Htoeenr [r, т- Y2 ( r - 1)] H [r, т- Y2 ( r - 1)] .

Вычисление оригиналов правильных дробей проводится методами компьютерной математики в среде Maple 18.

Для регулярной части одной из функций влияния без громоздких выкладок может быть получен явный вид:

G to rr o r ( ^{r , T} ) = ^H to rr o r ^{[ r , T-} Y o ( ^{r - 1} ) ^{] H [t-} Y o ( ^r - 1 ) ] ^,

Htorror (r, t) = -(r -1) r-2 [Y-1 + 2аи(т + Yor)] e-Tho.

• 7.    Примеры

В качестве примера рассмотрим среду в виде композита из алюминиевой дроби в эпоксидной матрице со следующими физическими характеристиками [2, 32]:

ц = 1,89 Г П a ; c 1 = 2,28 Ю³ м/с ; c ₂ = o,929-Ю³ м/с; c 3 = 2,48-Ю³ м/с; J = o,429-Ю ^{- 3} кг/м ; a = 7,45 МПа .

Скорость c ₄ находим с помощью формулы, указанной в [35, 36]:

c ₄ = c ₃ ^ 1 + аДр с ₂ ² ) = 2,485 - 1o³ м/с.

Принимая характерный линейный размер, получаем необходимые безразмерные параметры:

Y o = o,918; Y 1 = 2,45; Y 2 = o,919;

a' = o,654 - 1o^-3; u = 5,1o - 1o⁶.

На рис. 1, 2 представлены результаты расчетов для регулярных составляющих функций влияния G _{to rr} 1 _r и G toe61 r . Два фронта волн - т = Y o ( r - 1 ) и т = Y 2 ( r - 1 ) -здесь сливаются в один разрыв первого рода в силу того, что для используемой среды имеет место приближенное равенство Y _o "Y 2 .

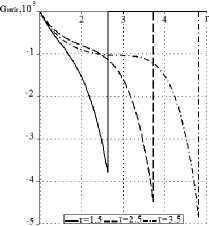
Рис. 1. Распределение регулярных составляющих функций влияния G ω rr 1 r и G ωθθ1 r по радиусу в различные моменты времени

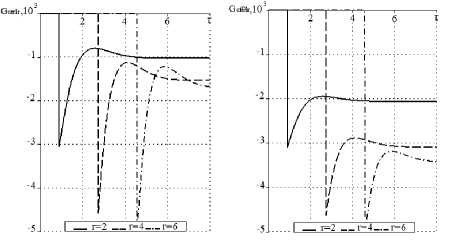
Рис. 2. Зависимость регулярной составляющей функции влияния G ω rr 1 r и G ωθθ1 r от времени при различных значениях радиуса

Fig. 1. Distribution of the regular components of the influence functions G ω rr 1 r and G ωθθ1 r along the radius at different points in time

Заключение

В линейном приближении по малому параметру аналитически построены поверхностные функции влияния для перемещения и углов поворота в задаче о распространении нестационарных антисимметричных кинематических возмущений от сферической полости в упругом моментном пространстве. Показано, что имеются три волновых фронта, соответствующие модифицированной с учетом свободного вращения волне сдвига и двум волнам вращения. Предложенный алгоритм решения может быть использован как для построения остальных функций влияния, так и для задач с силовыми возмущениями.