Распространение оптических вихрей в резонаторе ввода-вывода на основе вертикального массива кольцевых резонаторов

В последнее время наблюдается рост внимания к вопросам, связанным с теоретическими и прикладными аспектами распространения оптических вихрей (ОВ) [1] – частного случая так называемых структурированных световых пучков [2]. К настоящему времени достоверно установлена важность использования ОВ при создании разнообразных оптических сенсоров [3], оптических ловушек и других средств сортировки и манипулирования микрочастицами [4–6]. ОВ находят применение в микроскопии [7, 8], астрофизике [9– 11] и в ряде других областей современной физики. Наиболее перспективным приложением ОВ представляется использование их для передачи информации в оптических линиях связи [1, 12].

Подобная устойчивая тенденция в информационной оптике связана с тем, что ОВ образуют в гильбертовом пространстве базис взаимно ортогональных состояний, на которых может осуществляться независимое кодирование информации. При отсутствии перекрёстной связи между такими каналами теоретически возможна передача по ним на одной частоте любого объёма информации. Особый интерес представляет возможность передачи ОВ по оптическим волокнам, что существенно расширяет перспективы использования ОВ в информационной оптике [13].

Рост применения передаваемых по оптическим волокнам ОВ [14] делает актуальным разработку и создание на базе многомодовых волокон средств управления характеристиками ОВ. Среди таких эле- ментов волоконно-вихревой фотоники особое место занимают оптоволоконные резонаторы. За время, прошедшее с момента первой демонстрации волоконно-кольцевого резонатора [15], было показано, что такие системы могут использоваться в качестве элементов оптических сенсоров [16, 17], при создании спектральных фильтров [18], для разделения волн и оптического мультиплексирования в резонаторах ввода-вывода [19].

Недавно была продемонстрирована способность петлевых [20, 21] и кольцевых [22] резонаторов осуществлять сверхэффективное параметрическое управление топологическим зарядом (ТЗ) ОВ. Было доказано, что в основе этого эффекта лежит многофотонная интерференция, возникающая при многократном туннелировании ОВ на участке связи. В наиболее явном виде эта идея выражена в микрокатушечных волоконных резонаторах (МКР), где ОВ могут туннелировать в соседние витки по всей длине волокна [23–25].

МКР на базе одномодового волокна, впервые исследованные Сумецким [26], являются представителями более широкого класса резонаторных массивов, включающего также такие типы массивов, как CROW [27] и SCISSOR [28]. Основным отличием МКР от последних двух типов массивов резонаторов является их непланарная трёхмерная (3D) сборка, что делает эту схему компактнее. Впоследствии в работе [29] была предложена альтернативная схема резонатора, которая является буквальным трёхмерным аналогом массивов плоских кольцевых резонаторов – вертикальный массив кольцевых резонаторов (ВМР). Такие структуры могут быть изготовлены с использованием технологий трёхмерной фотонной схемотехники [30] или других методов, как механических, так и интерферометрических [29]. В работе [29] были исследованы трансмиссионные характеристики ВМР, включённого в схему резонатора ввода-вывода.

В этой связи изучение прохождения структурированного света через резонатор ввода-вывода с элементом ВМР на базе многомодовых волокон представляется естественным продолжением предыдущих работ.

Целью нашей работы является исследование распространения ОВ в такой оптической системе. На основе реалистической теоретической модели, использующей скалярное приближение, показана сводимость этой задачи к задаче о независимом прохождении через такую систему чётных и нечётных мод Лагерра–Гаусса (ЛГ).

Мы установили, что эволюция каждой из таких ЛГ-мод может быть описана эволюцией поля в некотором эффективном одномодовом волокне. Мы изучили характеристики пропускания ОВ и показали, что соответствующие кривые пропускания имеют характерную щелевидную структуру, наличие которой мы объясняем проявлением зонной структуры бесконечной стопки связанных кольцевых резонаторов. Кроме того, мы оцениваем пригодность ВМР в качестве элементов линий задержки для волоконнооптической связи, использующих в качестве носителей информации состояния с собственным орбитальным угловым моментом (ОУМ). Показана принципиальная возможность использования ВМР для таких целей. В частности, мы подчеркиваем преимущества использования таких систем в качестве линий задержки для связи, использующей в качестве носителей сигналов не ОВ, а нечётные и чётные моды ЛГ.

1. Модель

Есть несколько схем включения ВМР в оптические цепи, отличающихся взаимным расположением ВМР и прилегающих волокон. Рассмотрим сначала включение ВМР по схеме фильтра ввода-вывода, при которой стопка из N–2 связанных кольцевых резонаторов с периметром l 1 + l 2 спарена на участке длины l 1 с волокном-шиной и дополнительным волокном, расположенным по одну сторону (см. рис. 1 а ). Используя подход, изложенный в [26, 31], мы вводим на сегментах резонаторов и соединительных волокон длины l 1 медленные амплитуды P i ( s 1 ), Q i ( s 1 ), которые определяют композицию оптического поля на этих отрезках: [ P i | о , /) + Q i\ o , -l) J exp( i P , S 1 ). При этом мы полагаем, что характерный пространственный масштаб изменений амплитуды, «медленность» множителей P i ( s 1 ), Q i ( s 1 ), много больше аналогичной величины для множителя exp( z p , s 1 ), равной 1/ в . Здесь 0 <  s 1 <  l 1 -координата, отсчитываемая от начала каждого сегмента, в - скалярная постоянная распространения. Кет-вектор

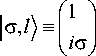
exp( il ф ) F _t ( r ) ^ col ( 1, i о ) exp( il ф ) F _t ( r ),

l = ± I ( I = 1,2,3...), о = ± 1 - определяет тип круговой поляризации, и F ℓ – радиальная функция моды идеального волокна. Как обычно, мы подразумеваем полярные координаты (r, ф ), введённые в поперечном сечении [31]. Поле | о , l ) имеет в центре r = 0 фазовую сингулярность с ТЗ l и представляет собой ОВ. Аналогично, на N-1 связанных участках длины l 2 введём д о полн и тельный набор медленных амплитуд P ( s ₂), Q ( s ₂) , где i = 2.. N , и координата 0 < s 2 < 1 2 отсчитывается от начала такого участка. Тогда можно записать систему уравнений для введённых медленных амплитуд:

. dA —4

- 1 —¹ = k A -

ds 1

dA 2

ds ₁

/х

= KI

,

—

. dBi —5

-1 - = KB3

ds ₂

—* dB 3

ˆ

-1---= K ds2

,

dA N +1 _ a —

1 Л   = KAN ds

— dBN

- ds2

—

= K B n - 1

——                               ——          —       — где Am = COl(Pm (S1), Qm (S1)) , Bm = COl(Pm (S2), Qm (S2)), и

K =

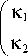
K 2

K 1

составлена из констант связи K 1 и к ₂, описывающих

туннелирование ОВ в соседнее волокно без или с инверсией его ТЗ соответственно. Подробности

получения выражений для констант связи можно

найти в [31].

а)

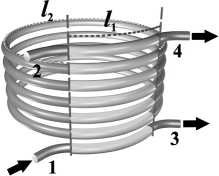
Рис. 1. Схема одностороннего (а) и разностороннего (б) включения фильтра ввода-вывода на основе ВМР. Входной и выходной отрезки оптоволокон входят в соединительные отрезки длины l 1 . Сегменты колец, не спаренные с входящими волокнами, имеют длину l 2 . Вертикальными пунктирными линиями отмечены границы, где происходит

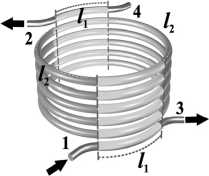
изменение числа связанных волокон

Над этими системами уравнений можно сделать диагонализирующее матрицу K преобразование:

А Л — ^—         ^т — ^т ^—

K —^ C K C , { A m , B m } — ^ { CA m , CB m

= { col( n m , V m ),COl( n m , V m ) } ,

где

1 f 1 1 ) 72 1 1 - 1 /

( A m , B m ) — это или ( п m , П m ), или ( v m , v m ), тогда как k - это или к ₊, или K _— соответственно. В таких обозначениях граничные условия выглядят так:

Это приводит (1) к четырём расцепленным системам уравнений относительно неизвестных

П m = [ P m ( 5 1 ) + Q m ( 5 1 ) ] /72, v m = [ P m ( 5 1 ) - Q m ( 5 1 ) ] / 72, П m = [ P m ( 5 1 ) + Q m ( 5 1 ) ] /72, v m — ^[ P m ( 5 1 ) - Q m ( 5 1 ) ] /72.

Этот математический факт имеет ясную физическую интерпретацию. Действительно, очевидное соотношение:

B m ( 0 ) = e ^el 1 A m ( 1 1 ) , A m ( 0 ) = e »' l 2 B m ( 1 2 ) , A ( 0 ) = 1, i >  2.

Вводя вектор-столбец a ( 51 ) = col[ A ( 51),... An+1 ( 51)], можно записать формальное решение (5), (6) в следующем виде:

a ( 1 1 ) = [ 1 - e iM 1      M 2 ] " ' e iM 1 l - a ,^ .                   (7)

P m |O ,') + Q m |O, - ') — П m "12 (| o , ^ + | G , —^ ) +

+v m ^72 (I °’ ^ — 1°, -^ )=                         (3)

= п m|ev ) + v m\od\

Здесь матрица M 1 имеет ранг N +1, а её элементы определяются как

^M pq = ^K ( ⁸ p + 1, q +8 p , q ₊ 1 )

где 8 jj - символ Кронекера. Помимо этого,

(и аналогичное соотношение для амплитуд с чёрточками) доказывает, что новые амплитуды описывают поля ВМР как разложение по чётным | ev ) и нечётным | od ) комбинациям ОВ. Тот факт, что система (1) расцепляется в новых амплитудах, означает, что и поля, запущенные в ВМР из волокна-шины, будут распространяться в нем независимо друг от друга. Таким образом, в скалярном приближении можно свести задачу о распространении мод высшего порядка через ВМР к двум независимым задачам, связанным с распространением фундаментальных мод. При этом роль этих фундаментальных мод должны играть чётные | ev ) и нечётные | od ) ЛГ-моды, а константы связи для этих мод должны быть приняты за к ± = к 1 ± к ₂ соответственно. Для получения уравнений для медленных амплитуд ( п _m , П _m ), ( v _m , v _m ) необходимо сделать в (1) последовательные формальные замены:

( A m , B m ) ^ ( п m , П m ) K ^ K + K 2 ;

- -          -                                (4)

( A m , B m ) ^ ( v m , v m ); K > K' -K 2 .

В дальнейшем мы будем обращаться к этим воображаемым ситуациям с эффективными одномодовыми волокнами, опуская в системе (1) векторы над ( A m , B_m ) и шляпки над K , так что в её аналоге

„ f0

M 2 — ...

... 0 ^

pi^{M 2 1 2} e ...

... 0 ,

где элементы матрицы M 2 ранга N –1 так же описываются формулой (8).

Для разносторонней схемы подключения (см. рис. 1 б ) уравнения для медленных амплитуд в системе на базе эффективного одномодового волокна имеют вид:

dA ₁

ds 1

dA ₂

— K A ₂

■ dA 2     „

- г —2 — kA3' d51

ds 1

( A 1 + A 3 )

dAN

-,----— kAj ds1

- ,dB — K B з ds 2

. ^dA 3       / ,      , \

-i—= k( a2 + A4) ds1

-

. ^dAN + 1      -1

-,—-- — K AN d⁵ 1

dB 2

-,---- ds2

— K B ₃ 3

-i dB- — K(b2 + b4) -i dB^ — K(b2 + b4)

4 d5 2                   , <  d5 2

dB N

¹ J ^—KB N - 1 ds 2

_idB N ds 2

^{— k B}N - 1

■ dA 1       л - , ---— к А 2 d5 1	. dB 2 _ - , ----— k B 3 ds 2
. dA2        / . . \ - , — — k ( A 1 + A 3 ) 4      d5 1                      ,	. dB 3      / x - i —:— — K ( B 2 + B 4 ) ds 2 .	(5)
.. - idA N + 1 — K A N d5 1	- idB N — k B n - 1 d5 2

Неизвестные амплитуды A i , B i относятся к первым двум сегментам с длинами l 1 и l 2 соответственно (если смотреть сверху и обходить стопку резонаторов по периметру против часовой стрелки, начиная от порта 1), а амплитуды A , , B , - ко вторым сегментам с длинами l 1 и l 2 соответственно. Отметим, что число неизвестных амплитуд A i , А , '- N , а B i , B , - N - 1. Граничные условия имеют вид:

A ( 0 ) = B i ( 1 2 ) e i^{e 1} 2 , A ( l i ) ^{1 1} = B ( 0 ) ,

A'(0) = Bi( 12)eie 12, Ai'(li)eie 11 = Bi(0), где 2 < i < N. Используя аналогичную технику решения, как и в предыдущем случае, можно получить формальное решение этой системы:

A ( 1 1 ) = [ 1 - e ^{2 i} ₽ ( ^{1 i + 1 2} ) M ₂ M c e iM i ^ M ₂ M - ]^{- 1} , e ^{iM 1 l 1} A in ,                                                          (10)

A' ( 1 1 ) = e i^{e 1 1 + 1 2} ) e^{i M} 1 ^kM ₂ M . A ( 1 1 ) .

Здесь

( 0

M . =

, M 2 =

e iM 2 l 2

Заметим, что матрицы M c и M 2 имеют ранги N ; 1 ^ˆ – единичная матрица ранга N –1. В M c первая строка и последний столбец содержат только один ненулевой элемент:

[ M . 1 1 , = 1.

• 2 . Характеристики пропускания

0.4995 0,5 0,5005 0,501

Очевидно, кривые пропускания через изучаемую систему определяются значениями медленных амплитуд P 1 ( 1 1 ), Q 1 ( 1 1 ) и P ,+ 1 ( 1 1 ), Q n+ 1 ( 1 1 ), связанными с n m , v m посредством P m = ( n m + v m ) /72 , Q_m = ( n _m - v _m ) / V2 . Точные значения неизвестных л _m , v _m можно найти из систем (5) для ВМР-фильтров ввода-вывода на базе эффективных одномодовых волокон с константами связи к ± .

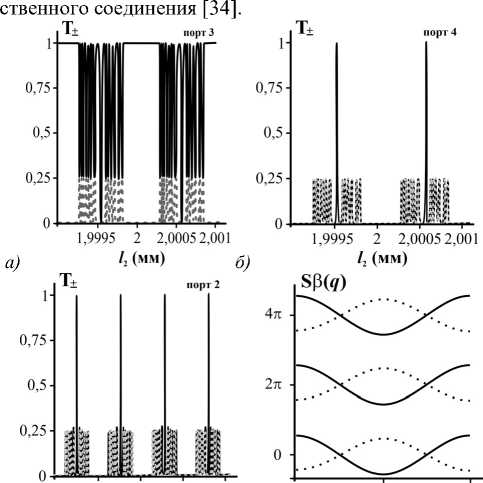
На рис. 2 показаны кривые пропускания для фильтра с элементом ВМР с восемью кольцевыми резонаторами; падающее поле – ОВ с ТЗ +5. Как видно (рис. 2а,б), данные кривые имеют выраженные зоны пропускания, разделённые «запрещёнными» участками. Можно отметить, что кривые пропускания ОВ имеют форму гребёнок. При наличии в этих портах средств разделения ОВ по знаку ТЗ в них можно организовать вихревые частотные гребёнки. Заметим, что этот способ генерации таких гребёнок оказывается предпочтительнее в сравнении с аналогичными схемами с использованием систем с нарушенной РТ-симметрией [32]. Стоит отметить, что при второй схеме подключения (рис. 2в) гребёнка на выходе из порта 2 плотнее аналогичной гребёнки, получаемой при первой схеме подключения. Это объясняется тем, что при такой схеме длина кольцевого сегмента (l2) в нашей модели увеличивается в два раза по сравнению с первой схемой (см. первую формулу (10)). Необходимо также отметить, что при врезке резонатора в линию связи нужно обращать отдельное внимание на качество соединения внешнего волокна с каким-либо из портов, так как нарушение соосности волокон мо- жет привести к появлению паразитных полей со значительными амплитудами [33]. Тем не менее, существуют современные методы контроля сварки двух добиться каче- оптических волокон, позволяющих

в)

г)

/2 (мм)

л         2л q (рад)

о

Рис. 2. (а – в) Зависимость мощности передаваемых ОВ от длины участка спаривания 1 2 при возбуждении ОВ |1,5 ) . Сплошные кривые - мощность ОВ 11,5 ) ; точечные кривые -мощность ОВ |1, - 5 ) . (г) Спектр постоянных распространения нормальных мод бесконечной стопки связанных кольцевых резонаторов; безразмерные параметры связи K + = – 0,88, K – = 0,72. Сплошная кривая относится к случаю с константой связи к + , а точечная - к случаю с константой связи к - . Параметры: 1 1 = 1 мм, волноводный параметр А = 9,5 - 10 ^-3, n .o = 1,5, радиус сердцевины r o = 10 X a , длина волны Л о =1550 нм

Для объяснения причин возникновения такой специфической структуры кривых пропускания следует обратиться к выражениям для спектров нормальных мод бесконечной стопки связанных кольцевых резонаторов. Как показано в [29], спектр постоянных распространения в ( q ) нормальных мод такой системы равен

S Р ( q ) = 2 п n - 2 k S cos q ,

где S – длина окружности кольца, n – целое число, нумерующее спектральную ветвь, q – безразмерный квазиимпульс q-й нормальной моды. Для нашего случая существуют два значения констант связи - к±, которые определяют спектральные кривые для упомянутых выше ВМР на базе эффективных одномодовых волокон. Также мы полагаем S = l1 + l2. Графики таких спектральных кривых приведены на рис. 2г. Как видно, спектр имеет ярко выраженную зонную структуру. При малых значениях безразмерных констант связи к± S ^ K± запрещённые зоны спектра ярко выражены. Можно показать, что с увеличением значений K± ширина щели в спектре уменьшается. Это приводит к сокращению «запрещённых» зон в кривых пропускания, а при достаточно больших K± – к их полному исчезновению и формированию в системе стохастической кривой пропускания.

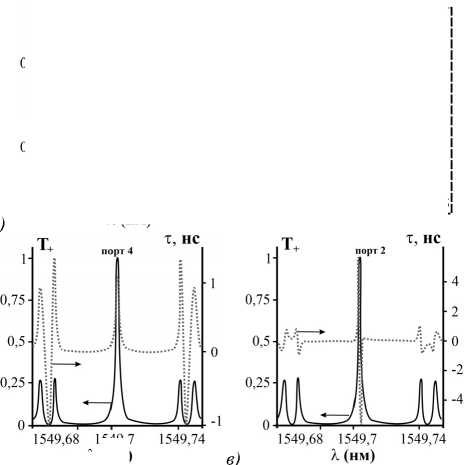
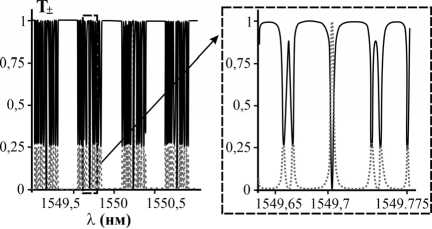
Вполне естественно, что картина пропускания, представленная на рис. 2 а, б, в , воспроизводится и в спектральном диапазоне. На рис. 3 а представлены соответствующие частотные гребёнки для первой схемы подключения (рис. 1 а ). Группы пиков пропускания с разносом 66,5 ГГц разделены запрещёнными зонами шириной 25 ГГц. Ширина отдельных узких пиков – порядка 0,2 ГГц. Тонкая структура таких пиков показана на вставке к рис. 3 а .

Как и другие волоконно-резонаторные структуры [31], ВМР способны замедлять световые импульсы и могут служить элементом линии задержки. Время групповой задержки (ВГЗ) t d определяется как: t d =– d Φ / d ω [32], где Φ – фаза передаваемого поля, ω – круговая частота. В нашем случае, когда

б)

1549,7

Л (нм)

Рис. 3. (а) Мощность ОВ |1,5 〉 на выходе из портов 3 (сплошная линия) и 4 (точечная линия) в зависимости от длины волны при возбуждении ВМР ОВ. На вставке указана тонкая структура. Мощность и ВГЗ для ОВ |1,5 〉 в зависимости от длины волны на выходе из портов 4 (б, 1ая схема подключения) и 2 (в, 2-я схема подключения).

Падающее поле – ОВ |1,5 〉 . Сплошная линия – мощность ОВ |1,5 〉 (левая вертикальная ось), точечная линия – ВГЗ (правая вертикальная ось). Параметры системы: l 1 = 1 мм, l 2 = 2 мм (а, б) и l 2 = 0,5 мм (в), остальные как на рис. 2

выходящее поле представляет собой взвешенную сумму парциальных ОВ |1, ± ℓ〉, ВГЗ следует рассчитывать отдельно для таких составляющих. Таким образом, для получения значений ВГЗ для ОВ |1, ± ℓ〉 необходимо определить фазы Φ± таких ОВ. Разумеется, эта чисто математическая процедура подразумевает возможность выделения из суперпозиции ОВ полей с разными ТЗ, что может быть достигнуто рядом существующих экспериментальных методик. На рис. 3б, в показаны кривые пропускания и ВГЗ для положительно заряженных ОВ на выходе из портов 4 и 2 соответственно. Заметим, что для выходящего порта 3 ВГЗ на горизонтальных участках кривых пропускания для ОВ близко к нулю, а там, где его значение принимает значения порядка нескольких наносекунд, мощность ОВ стремится к нулю (см. вставку к рис. 3а), поэтому мы не приводим соответствующие графики. Стоит также отметить, что максимум ВГЗ для системы со вторым типом подключения (рис. 3в) наблюдается примерно при 80 % пропускании ОВ. Тем не менее, данный недостаток компенсируется тем, что вблизи пика прохождения исходного ОВ для выходящего порта 2 ОВ с противоположным знаком ТЗ имеет крайне малую интенсивность.

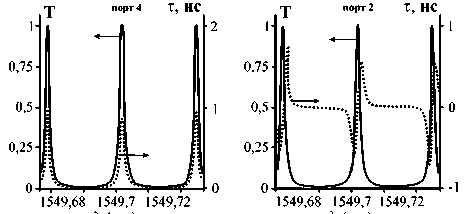
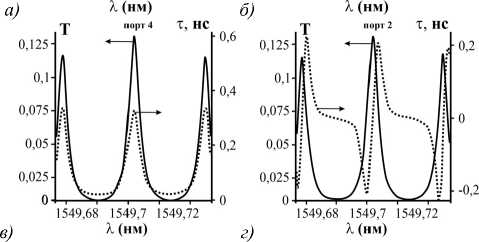
Рис. 4. Мощности чётных мод ЛГ на выходе из портов 4 (а, в, модель на рис. 1а) и 2 (б, г, модель на рис. 1б). (а, б) γ = 2,3 ⋅ 10 –3 м -1 , (в, г) γ =10 м -1 . На вход подаётся чётная мода ЛГ. Параметры: l 1 = 1 мм, l 2 = 2 мм, остальные как для рис. 2

В рамках скалярной модели чётные и нечётные моды ЛГ являются собственными модами рассматриваемого нами резонатора и могут быть использованы при мультиплексировании/демультиплексировании [35]. На первый взгляд кажется, что при подаче мод ЛГ на вход резонатора (порт 1) они должны проходить через него с приобретением только дополнительной фазы (как в ВМР на одномодовых волокнах). В этом случае отпадает необходимость оптимизации параметров резонатора таким образом, чтобы необходимое значение ВГЗ достигалось при мощностях ОВ, близких к мощности исходного ОВ. Тем не менее, такое поведение будет иметь место только для ВМР, нагруженного одним волокном. В изучаемых в рамках данной работы моделях ВМР с двумя волокнами может появляться дополнительный эффект, а именно перекачка энергии входящего поля между выходя- щими портами. На рис. 4 приведены графики для зависимости мощности выходящей из резонатора чётной моды ЛГ и ВГЗ для неё от длины волны падающего излучения. Заметим, что кривая для ВГЗ на проходящем порте 3 для любой схемы подключения ведёт себя аналогично кривой для ВГЗ в случае возбуждения системы ОВ. При ничтожно малых мощностях мод оно достигает значений порядка наносекунд, на остальных участках почти равно нулю. Заметим, что в резонаторе возбуждается только чётная мода ЛГ, и на любом из выходов резонатора отсутствует нечётная ЛГ-мода. Графики на рис. 4а, б построены для случая, когда в системе присутствует затухание, отвечающее затуханию реальных прямых многомодовых волокон. Заметим, что для его учёта необходимо произвести замену βl→βl+iγ. В изучаемой нами системе, помимо традиционных потерь, присутствуют существенные радиационные потери, обусловленные изгибом волокна. При радиусе изгиба волокна порядка нескольких миллиметров изгибным потерям отвечает значение коэффициента затухания γu ~ 10 м –1 [36]. Из рис. 4в, г видно, что при таких значениях γ система может выполнять свои функции.

Заключение

В заключение мы исследовали передачу мод ЛГ и ОВ по волокну, нагруженному вертикальным массивом кольцевых резонаторов. Мы показали, что кривые пропускания для ОВ имеют характерную щелевидную структуру, которую мы объяснили как проявление зонной структуры бесконечной стопки связанных кольцевых резонаторов. Мы показали, что можно использовать ВМР в качестве элементов линий задержки для оптоволоконной связи на высших модах ЛГ и ОВ.

Данная работа выполнена при поддержке Российского научного фонда, Проект № 23-22-00425.