Распространение терагерцовых импульсов в капиллярных волноводах с металлизированной границей

В настоящее время активно проводятся работы по проектированию и оптимизации волноводов для передачи электромагнитного излучения терагерцового (ТГц) диапазона частот. Такие волноводы востребованы в астрономии, при дистанционном зондировании объектов (в частности, тканей при их медицинской диагностике), для ТГц-спектроскопии во временной области газовых компонентов в воздухе и т.д. [1, 2].

Мощное ТГц-излучение могут генерировать лазеры на свободных электронах [3]. Однако их применение ограничено высокой стоимостью, габаритами и сложностью в эксплуатации. Сейчас более распространены импульсные источники ТГц-излучения, принцип действия которых основан на нелинейном преобразовании оптических лазерных импульсов в ТГц-диапазон с помощью фотоантенн [1, 2]. Получаемые таким образом ТГц-импульсы в большинстве случаев имеют ширину полосы частот, сравнимую с несущей частотой. В результате ТГц-волноводы должны обеспечивать передачу широкополосных сигналов. Создание ТГц-волноводов осложнено и тем, что все известные материалы сильно поглощают ТГц-излучение. Исключение составляет сухой воздух. Поэтому наиболее перспективны волноводы, передающие ТГц-излучение по полой сердцевине [1]. Среди них эффективны диэлектрические капилляры кругового сечения с металлизированными границами [1, 2, 4–7]. Известны два типа таких волноводов: волноводы типа 1, у которых металлическое покрытие микронной толщины, превышающей толщину скин-слоя, нанесено на внутреннюю поверхность диэлектрического капилляра [4, 5, 7], и волноводы типа 2, которые отличаются от волноводов типа 1 наличием дополнительного диэлектрического слоя с диэлектрической проницаемостью εL = ε′L + iε′L′ и толщиной d, который находится между металлическим покрытием и полой сердцевиной [4, 6]. Данный слой служит для минимизации затухания основной моды волновода на частоте f за счет изоляции её поля от металлического покрытия. Приближенно такая минимизация достигается при условиях [8]

k 0 d = ( ε′ L - 1) ^{- 0,5}{ s tan ^{- 1}[( ε′ L ( ε′ L - 1) ^{- 0,5})^0,5] + l π }, (1)

где s = ± 1, l =0, 1,… при s = 1, l = 1, 2,… при s =–1, k 0 = 2 π fc ^–1 – волновое число излучения в вакууме, с – скорость света.

В работах [4–6] основное внимание уделено расчёту затухания мод волноводов в случае монохроматического излучения. Пропускание через волноводы широкополосных ТГц-импульсов исследовалось только экспериментально с использованием сравнительно коротких отрезков волноводов, длина которых не превышала 45 см [6, 7]. Слабо исследованы и вопросы ТГц-спектроскопии во временной области примесных компонентов в воздухе, заполняющем полую сердцевину волноводов. Качественные соображения, приведенные в [9], позволяют лишь предположить, что основным ограничивающим фактором при такой спектроскопии может быть многомодовый режим работы капиллярных волноводов с металлизированной границей, который неизбежен при передаче широкополосных импульсов.

В настоящей статье разработана техника расчёта распространения широкополосных ТГц-импульсов в протяжённых волноводах, в которой поле импульса представляется в виде суперпозиции импульсов полей отдельных волноводных мод, найденных интегрированием монохроматических компонент. Выполнен сопоставительный анализ капиллярных волноводов обоих указанных выше типов с позиций максимизации коэффициента передачи энергии импульса через волновод и восстановления спектра поглощения примесного компонента в воздухе, заполняющем полую сердцевину волновода, методом ТГц-спек-троскопии. В качестве примесного компонента рассмотрен водяной пар.

• 1.    Расчётные соотношения

Пусть на входной торец волновода, находящийся в плоскости z = 0, поступает линейно поляризованный вдоль оси 0 у ТГц-импульс, создаваемый фотоантенной. Воспользуемся моделью этого импульса [10]

E_y = A exp( - r ² w ^{- 2}) P ( t ),

где E y - компонента напряженности электрического поля, A - амплитудный множитель, r = ^ x ² + у ² , w -радиус Гауссова пучка,

P ( t ) = - 1,229 U ( - 2, -Z V2)exp( - 0,5 Z ²), (3)

U (...) - функция параболического цилиндра [11], Z = tT^-1, t - время, T - масштабный фактор, который может регулироваться длительностью и условиями фокусировки оптического лазерного импульса [10, 12]. Фурье-образ функции (3) имеет вид

P ( f ) = - 0,6143( Vn ) ^{- 1} Т exp( - 0,25 Q ²) x

∞j             j xZl Пl    |Z[Aj"Sk’ -i(j + 0,Wj2)Sj’], j=0 t l=1   4 J k=0

где Q = 2 n f T и имеют место рекуррентные соотношения

A ( p ) = AjP ) (4 j - 7 + p )[2 j (2 j - 1 + p )] ^{- 1},

A0) = -rf4J24 (Vn)-1, A(2) = -Гf4J24 (vn)-1, sj) = - Sk-j (j - k + 1)Q2 [2 k (2 k -1 + p )]-1,

О(0) _ 0(2)

S0 j = S0 j = 1 , где Г(.) - гамма-функция. Максимум |P(f )|, равный 0,2215Т, достигается на частоте f=0,2769Т1. В дальнейших расчётах выбрано значение Т= 0,2769 пс, при котором данная частота равна 1 ТГц. Графики функций (3) и (4) представлены на рис. 1 кривыми 1.

В свободном полупространстве z >  0 с диэлектрической проницаемостью £ поле импульса (2) описывается интегралом [13]

Ey ( x , у , z , t ) = 8 п ² zA Re J d fP exp( i2 n ft ) x

^ ^                               2 .   /2

1    + zk0 £r R    | x + у /- 1

x -----exp----- zk₀ £ r R dx d у ,

Rj               w2       "

-∞ -∞

где R = V( x - x )² + ( x - x )² + z ² . После перехода к цилиндрическим координатам (5) приобретает вид

Ey (r, z, t) = 4nzA exp(-r2 w-2) x xRe JdfPexp(i2nft)Jp(1 + ik0 V£R')R'3 x x10 (2rpw2) exp(-p2w2 - ik0 V£R')dp, где R' = 7p2 + z2 , 10 (...) - модифицированная функция Бесселя.

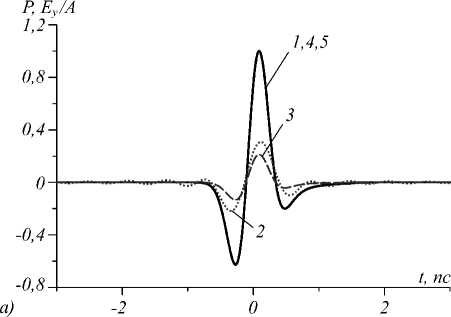
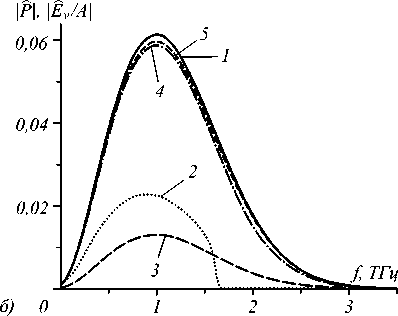
Рис. 1. Временная (а) и частотная (б) формы импульса на входе в волноводы и иллюстрация влияния числа учитываемых волноводных мод на точность расчётов.

Кривые 1 – модель (2), (3) и разложения (7), (8) для волноводов типов 1 и 2 при m ≥ 8; 3 (m = 1), 4 (m = 6) – волновод типа 1; 2 (m = 2), 5 (m = 6) – волновод типа 2 Рассматривая (6) в дальней зоне ( r ² + z ² ^«0 и учитывая связь между компонентами электромагнитного поля E и H , вытекающую из уравнений Максвелла, можно рассчитать полную энергию импульса (2) W ) , излучаемую в полупространство z >  0. Полагая £ = 1, находим:

^   2п^

W ₀ = J d t J d ^ J r ( E x H ) _z d r =

-^   0

8 n ⁵ w⁴

P 0 c³

∞

A ² J d ff ² x

• 2    1

x| / ’j J (1 + u ²)exp[0,5( k ₀ w )²( u ² - 1)]d u , 0

где ф - угол цилиндрической системы координат, у. 0 -магнитная проницаемость вакуума.

Электромагнитное поле импульса в волноводе, ориентированном вдоль оси 0 z , представим в виде суммы импульсов полей волноводных мод:

E ( r , ф , z , t )

H ( r , ф , z , t )

= A^^ | Ev (r, Ф, z, t) | Vt1 t Hv (r, Ф, z, t) J , где v - номер моды, m - число учитываемых мод,

E v ( r , ф , z , t )

H v ( r , ф , z , t )

∞

4 n Re J C v ( f )

f e v ^{( r} , ф , ^f ) 1 _x t h v ^{( r} , ф , ^f ) J^X

x exp { i [2 n ft - k 0 e v ( f ) z ] }d f ,

C v – амплитуда, β v – безразмерная постоянная распространения, e v и h v – векторы электрического и магнитного поля моды, z ≥ 0.

Энергия мод рассматриваемых волноводов практически полностью сосредоточена в диэлектрических средах. Поэтому выполняются соотношения ортогональности [14]

2π ∞ j dфj drr (e^X hV ) z = 8^ J dфj drr (ev X hV ) z ,(10)

где δµv – дельта-символ Кронекера, а звездочка означает комплексное сопряжение. Как следует из (2), (8) – (10), ∞ j drr exp(-r2 w2) j dфhVx

Cν =-Pˆ(f)0 2π ∞         0       .(11)

j d ^ j d rr ( e _vx h V ) _z 00

Согласно (11), амплитуды C v отличны от нуля только для тех мод волновода, у которых компонента поля h vx является четной функцией x и y . Такие моды являются аналогами HE 1 m мод круглого диэлектрического волновода. В разложении (8), (9) фигурируют только поля указанных мод, причем нумерация мод осуществляется в порядке убывания значений Re β v .

Строгий расчет модовых характеристик рассматриваемых в настоящей статье однослойных и двухслойных волноводов с цилиндрической симметрией может быть выполнен методом, изложенным в [15].

При исследовании ТГц-импульсов в протяженных волноводах может выполняться неравенство k 0 z >> 1. В этом случае численное интегрирование в (9) затруднено быстрыми осцилляциями подынтегральных функций. Избежать этой проблемы позволяет квадратурная формула

E _ν ( r , ϕ , z , τ )

H _ν ( r , ϕ , z , τ )

sin( π∆ f α ) _×            ν j

α

8 n Re £ C v ( j

e V ⁽ r , Ф , j ^x

( h v ⁽ r, Ф ^, fj) )

exp ^ ^{2 n} ifj ^{T- ( e (} fj) — 1)-_c,

где α_{ν j} = τ+ zc ^{- 1} - z υ^- _g ¹ _ν , t = t – zc ^–1, вещественная часть параметра υ _{g ν} = c ( β_ν + fd β_ν / df ) ^- _f ¹ _{= fj} имеет смысл групповой скорости моды. Выражение (12) получено в результате разбиения эффективного промежутка интегрирования в (8) на элементарные интервалы протяженности ∆ f с центрами на частотах f = f j и аналитического интегрирования на этих интервалах быстро осциллирующей экспоненты. Применение (12) оправдано, если ∆ f удовлетворяет условию

∆ f ² zc ^{- 1}(d β ν /d f + 0,5 f d² β ν /d f ²) f = f_j << 1.

Практический интерес представляет коэффициент передачи волноводом энергии ТГц-импульса. Определим этот коэффициент как отношение η = WW ₀ ^{- 1} , где W – энергия импульса, проходящая через поперечное сечение волновода с координатой z . В соответствии с (8) – (11)

∞   2π    ∞

W = j dt j dф j r(Ex H)z dr = £ WV ,(13)

-∞   0    -∞ где

∞

W v = 8 n 2 A ² j d f\C v| ² exp(2 k ₀ z Im e V ) X 0

2π ∞ x j dфj r Re(evX h)z dr - энергия импульса v-й моды.

Рассмотрим особенности волноводной ТГц-спектроскопии воздуха. Стандартный вариант метода ТГц-спектроскопии воздуха имеет дело с импульсами, распространяющимися в однородном пространстве [16]. Здесь с помощью регулируемой линии задержки измеряются импульсы E_y ⁰ ( τ ) и Ey (τ), прошедшие расстояние z между источником и приемником ТГц-поля через чистый сухой воздух и воздух с исследуемой примесью соответственно. Спектр коэффициента поглощения примеси k ( f ) определяется по формуле [16]

k ( f ) =- ( k 0 z ) ^{- 1}ln E ˆ y ( f )[ E ˆ y ⁽⁰⁾( f )] ^{- 1} ,

где E ˆ _y ( f ) и E ˆ _y ⁽⁰⁾ ( f ) – фурье-образы функций E y ( τ ) и E_y ⁽⁰⁾ ( τ ) соответственно. Одним из ограничивающих факторов при такой спектроскопии является значительная дифракционная расходимость широкополосного ТГц-излучения [16]. Аналогичный подход в случае использования волновода с полой сердцевиной позволяет устранить эффект дифракционной расходимости и за счет этого существенно повысить отношение сигнал/шум [7]. Вместе с тем волноводная ТГц-спектроскопия также имеет ограничения.

Пусть Ey(τ) и Ey0 (τ) представляют собой импульсы компоненты напряжённости электрического поля на выходе волновода в центре его полой сердцевины (техника измерения таких импульсов в локальных областях сечения волноводов описана в [9]). Предположим также, что выполняется естественное условие |∆n| << 1, где ∆n = Re∆n–ik( f ) – приращение показателя преломления сердцевины волновода n, вызванное наличием примеси в сухом воздухе. В этом случае заметное изменение фурье-образа поля (8) будет связано только с экспоненциальными множителями в (9), содержащими большой параметр k0z. В главном приближении л Ey(f) Eˆy(0)(f)

m

£ ^C V e V y exP ν = 1

m

£ C V e V y exp [ ^- ik 0 ^ev ^z ]

- ik ₀

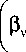
₊ ∂β ν _{∆ n} ∂ n

z

где функции частоты Cv( f ), evy(0, 0, f ), βv( f ), ∂βv( f )/∂n вычисляются при ∆n =0. Заметим, что в соответствии с теорией возмущений [14] мнимая часть производной ∂βv(f)/∂n пренебрежимо мала по сравнению с её вещественной частью (для исследованных ниже вол- новодов модули этих величин отличаются на 4 – 6 порядков). Поэтому производные ∂βv /∂n в (15) могут быть заменены на ∂Reβv /∂n.

В общем случае найти функцию k( f ) из уравнения (15) достаточно сложно. Ситуация упрощается, если на данной частоте при некотором номере µ exp(Im βµk0z) >> exp(Im βνk0z) (ν ≠ µ) .

Тогда волновод может рассматриваться как одномодовый, и в соответствии с (15)

k ( f ) =

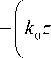
д Re в_ц 7 д n J

ln

Ey ( f )

E ˆ _y (0) ( f )

Выражение (16) сохраняет силу и в случае многомодового волновода, если зависимостью производных ∂β v ( f )/ ∂ n от номера моды можно пренебречь. Для рассматриваемых волноводов такая ситуация возникает, когда существенный вклад в суммы, входящие в (15), дают только моды, находящиеся в условиях, удаленных от критических, и ∂β v ( f )/ ∂ n ≈ 1 (см. параграф 2).

2. Импульс в волноводах

Расчёты выполнены для волноводов типов 1 и 2 с серебряным покрытием и внутренним радиусом B = 1,5 мм. Экспериментальные образцы таких волноводов демонстрируют приемлемые гибкость и затухание ТГц-сигналов [4, 5, 7]. Для задания диэлектрической проницаемости покрытия ε m использована дисперсионная модель Друде [17]:

ε =1- Ω2p -i   Ω2pΩt m      F2+Ωt2   F(F2+Ωt2) ,

где Ω p = 73381, Ω t = 147,376, F = 100 f /3, f берется в ТГц. Материалом диэлектрического слоя, отделяющего металлическое покрытие от полой сердцевины волновода, служит полипропилен с диэлектрической проницаемостью ε L = 2,229– i 3,88 ⋅ 10^–3 [18]. Толщина слоя d = 41,2 мкм. Она найдена из (1) при f = 1 ТГц, s = 1, l =0.

Поперечные сечения волноводов и нормированные интенсивности

S ν = S ν S ν ^- m ¹ ax , S ν = 0,5Re( e ν × h ^* ν ) z

их мод, которые имеют минимальное по сравнению с другими модами затухание, приведены на рис. 2.

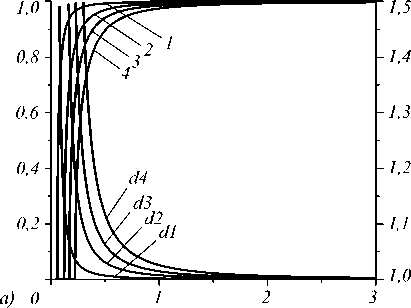
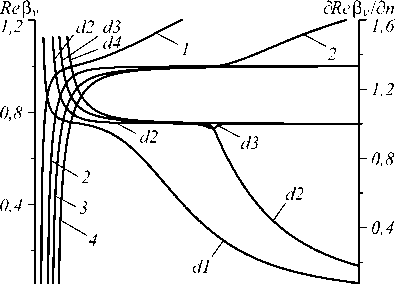
Дисперсионные свойства мод с указанной выше чётностью компонент h vx представлены на рис. 3. Они соответствуют показателю преломления n = 1 и диапазону f , в котором P ˆ( f ) заметно отличается от нуля (рис. 1 б ).

На рис. 3 функции Re β v ( f ) являются монотонно возрастающими. При уменьшении частоты графики этих функций вырождаются в вертикальные прямые линии, соответствующие критическим частотам. Данные частоты для мод волноводов типов 1 и 2 практически совпадают как между собой, так и с известными частотами отсечки круглого металлического волновода с идеально проводящими стенками [19].

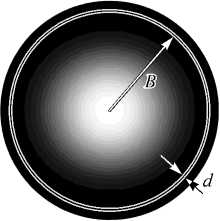
Рис. 2. Поперечные сечения волноводов типа 1 (а), (б), типа 2 (в) и распределения интенсивности их мод с номерами v = 1 (а),v = 3 (б),v = 2 (в) на частоте f = 1 ТГц

По мере приближения частоты к критическим значениям наблюдается резкий рост производных ∂ Re β v ( f )/ ∂ n и затухания мод. С ростом f для мод волновода типа 1 Re β v → 1, ∂ Re β v ( f )/ ∂ n → 1, |Im β v ( f )| → 0, что объясняется улучшением локализации полей этих мод в полой сердцевине волновода. Для каждой из мод волновода типа 2 при достаточно больших частотах выполняется неравенство Re β v > 1. В этом случае поле моды локализовано в основном в диэлектрическом слое и слабо взаимодействует с сердцевиной волновода. С этим связаны неравенства ∂ Re β v ( f )/ ∂ n <  1 при Re β v ( f ) <  1 (рис. 3 б ) и немонотонный характер зависимостей 1′–4′ на рис. 3 в . Для мод волновода типа 2 с номером v > 1 существует протяжённый интервал частоты, на котором Re β v ( f ) ≈ 1, ∂ Re β v ( f )/ ∂ n ≈ 1 (рис. 3 б ). В частности, эти равенства имеют место в окрестностях минимумов функций |Im β v ( f )|, соответствующих v =2 и v =3 (рис. 3 в ). Здесь поля мод с указанными номерами подобны полю основной моды HE 11 круглого диэлектрического волновода (рис. 2 в ). Затухание этих мод существенно ниже затухания остальных мод, что позволяет рассматривать волновод типа 2 в указанных областях частот как квазиод-номодовый. Заметим, что минимумы затухания мод 1 и 2 наблюдаются на частотах, заметно превышающих корни приближённого уравнения (1) (рис. 3 в ).

Re^v                               dRe^v/dn

б)0    12   3

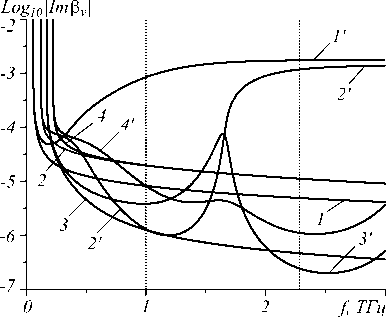
Рис. 3. Дисперсионные характеристики волновода типа 1 (а), типа 2 (б) и волноводов обоих типов (в, 1 – 4 – волновод типа 1; 1^'– 4^' – волновод типа 2). Кривые d1– d4 – зависимости ∂ Re β v ( f )/ ∂ n . В обозначениях кривых v, v′, dv v = 1,…, 4 – номер моды. Вертикальные штриховые линии – решения уравнения (1) при l = 0 и l = 1

Рис. 4 иллюстрирует энергетические характеристики волноводов, рассчитанные при m ≥ 8, n = 1.

Существование оптимальных значений w , соответствующих максимумам η на рис. 4, объясняется двумя конкурирующими процессами: уменьшением модулей амплитуд мод (11) при уменьшении w и уменьшением доли энергии импульса (2), попадающей в полую сердцевину волновода при увеличении w . Оптимальные значения w , соответствующие им значения η , а также относительные энергии импульсов мод, дающих основной вклад в суммарную энергию импульса (13), приведены в табл. 1 и 2.

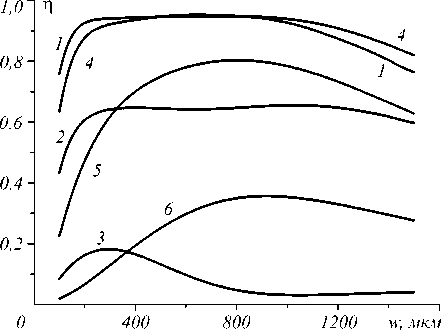
Рис. 4. Коэффициент передачи энергии импульса (2) волноводами типа 1 (кривые 1, 2, 3) и типа 2 (4, 5, 6) в зависимости от радиуса возбуждающего Гауссова пучка при m = 0,1 м (1, 4), 1 м (2, 5), 10 м (3, 6)

Табл. 1. Оптимальные условия возбуждения волновода типа 1

z , м	w opt , мкм	η max	W 1 / W	W 3 / W
0,1	793	0,948	0,729	0,041
1	1024	0,655	0,898	0,004
10	296	0,182	0,029	0,581

Табл. 2. Оптимальные условия возбуждения волновода типа 2

z , м	w opt , мкм	η max	W 2 / W	W 3 / W
0,1	646	0,952	0,750	0,125
1	800	0,803	0,889	0,079
10	919	0,357	0,940	0,059

Согласно рис.4, коэффициент η убывает при увеличении z , что объясняется затуханием мод. Как следует из рис. 4 и табл. 1, 2, оптимальные условия возбуждения волноводов зависят от z . Это, а также то, что максимальные значения W v / W заметно отличаются от 1, объясняется тем, что в волноводах распространяются импульсы нескольких мод, испытывающих различное затухание. В частности, в волноводе типа 1 при z =0,1 м и z = 1 м основной вклад в энергию суммарного импульса дает мода 1, поле которой лучше согласуется с радиально-симметричным полем Гауссова пучка, чем поле моды 3 (рис. 2 а, б ). В то же время при увеличении z до 10 м в волноводе типа 1 превалирует импульс моды 3, которая испытывает гораздо меньшее затухание в полосе частот входного импульса по сравнению с модой 1 (рис. 1 б, 3 в ). В волноводе типа 2 основной вклад в суммарную энергию импульса при всех рассмотренных z дает мода 2, которая испытывает минимальное затухание в полосе частот входного импульса (рис. 1 б , 3 в ) и имеет распределение поля, подобное Гауссову (рис. 2 в ).

В целом, согласно рис. 4 и табл. 1 и 2, волновод типа 2 обеспечивает более высокий коэффициент передачи энергии импульса по сравнению с волноводом типа 1.

Кривые 1–5 на рис. 1, рассчитанные при z =+0 и значениях w = 1024 мкм для волновода типа 1, и w = 800 мкм для волновода типа 2, выбранных в соответствии с табл. 1, 2, иллюстрируют внутреннюю сходимость принятой расчётной схемы. Здесь, в соответствии с (8), (9):

mm

EyA - 1 = £ E v y (0,0,0, t ), EyA - 1 = У C v ( f ) e _v y (0,0, f ).

ν= 1                                   ν= 1

Как следует из рис. 1, практически точное пред-

ставление поля импульса в волноводе в виде суммы полей импульсов мод и фурье-образа поля импульса в виде суммы фурье-образов полей импульсов мод достигается при выборе m ≥ 8.

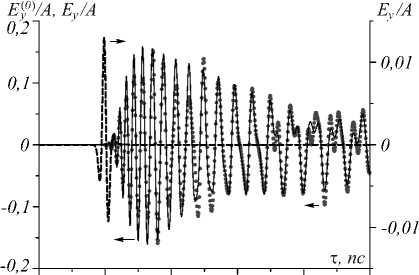
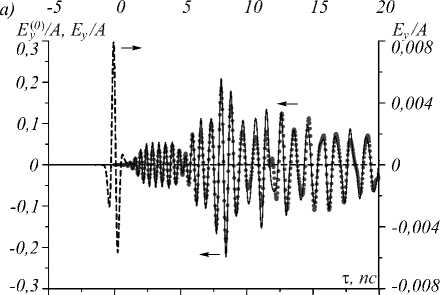
На рис. 5 приведены импульсы компоненты поля E y в волноводах типов 1 и 2 и в свободном пространстве при r =0, z = 1 м. Вычисления выполнены на основании квадратурной формулы (12) при выборе эффективного диапазона интегрирования в (9) 4 ТГц ≥ f ≥ 0 ТГц (рис. 1 б ). Результаты, устойчивые относительно задания частотного шага ∆ f , получены при ∆ f ≤ 0,01 ТГц. Поля импульсов в свободном пространстве рассчитаны по формуле (6).

импульса в свободном пространстве на рис. 5 а по сравнению с рис. 5 б .

На рис. 5 б можно отметить разделение импульса на два. Левый импульс с более высокочастотным заполнением сформирован гармониками с частотами, находящимися в окрестности правого минимума зависимости 3′, а правый соответствует окрестности минимума зависимости 2′ на рис. 3 в .

3. Волноводная ТГц-спектроскопия

Дискретными точками на рис. 5 представлены импульсы, соответствующие заполнению сердцевины волновода влажным воздухом. Для задания ∆ n использована модель Друде –Лоренца

A n = £ aj[bj(f f - f 2 ) + ifb^^x ,                (17)

j = 1

где f берется в ТГц, а параметры a j , b j , f j определены путем интерполяции экспериментальных данных для спектра k ( f ) = –Im ∆ n ( f ), измеренного в лабораторных условиях в диапазоне частот 0,24 ТГц – 2,6 ТГц в [20]. Значения a j , b j , f j , существенные для диапазона 1,5 ТГц ≥ f ≥ 0,5 ТГц приведены в табл. 3.

б)

Рис. 5. Импульсы при w = 1024 мкм (а, волновод типа 1) и w = 800 мкм (б, волновод типа 2).Сплошные кривые

соответствуют сухому воздуху (n = 1), дискретные точки – влажному воздуху. Штриховые кривые – импульсы в свободном пространстве с n = 1

Заметим, что форма импульса на выходе волновода типа 1 (рис. 5 а ) качественно согласуется с экспериментальными данными, приведенными в [7].

Согласно рис. 5, несмотря на дисперсионное расплывание импульсов в волноводах, амплитуда их колебаний значительно превосходит амплитуду колебаний импульсов в свободном пространстве, где дисперсионное уширение отсутствует. Этот результат является следствием дифракционной расходимости импульсов в свободном пространстве. Данная расходимость уменьшается с ростом радиуса пучка, что объясняет более значительную амплитуду колебаний

Табл. 3. Константы модели (17)

j	a j ⋅ 109, ТГц3	b j ⋅ 103, ТГц	f j , ТГц
2	3,33	9,98	0,557
3	2,42	9,98	0,752
4	1,91	9,98	0,988
5	8,42	9,98	1,096
6	3,07	9,98	1,112
7	7,19	8,14	1,162
8	3,12	9,38	1,206
9	3,16	9,98	1,228
10	4,97	7,62	1,411

Для моделирования метода волноводной ТГц-спектроскопии использовано выражение (14), где

^Ey ^{( f} )

Е0ЧП

V y ^{v J} ' 7

τ f

=I

τ _i

( E,(°,O,z, T ) ) _v E "’(0,0, z ', T ),

exp( - i 2 π f τ )d τ ,

импульсы E y (0, 0, z , τ ) и E_y ⁽⁰⁾ (0,0, z , τ ) соответствуют показателям преломления сердцевин волноводов n = 1+ ∆ n и n = 1. Расчёт этих импульсов при z = 1 м, τ i = –5 пс, τ f = 200 пс выполнен по схеме, описанной в предыдущем параграфе. Для имитации измерительных погрешностей к значениям E y и E_y ⁽⁰⁾ , рассчитанным при шаге τ , равном 0,03 пс, добавлялись смещения, полученные нормальным генератором случайных чисел с дисперсией, соответствующей отношению сигнал/шум = 1000. Численное интегрирование в (18) выполнено методом трапеций.

Результаты восстановления функции k ( f ) в диапазоне 1,5 ТГц ≥ f 0,5 ТГц приведены на рис. 6.

Рассмотрение рис. 6 позволяет заключить, что метод волноводной ТГц-спектроскопии в целом пригоден для восстановления спектра поглощения примесного компонента.

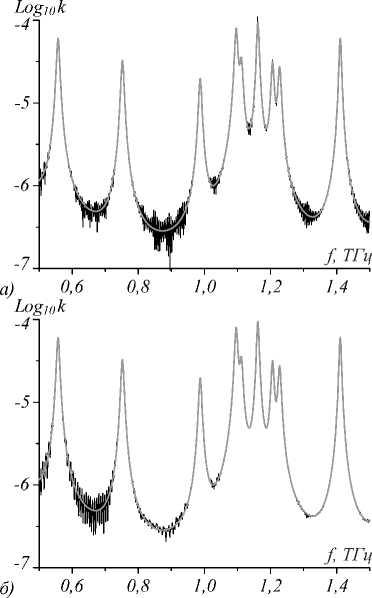
Рис. 6. Восстановление спектра коэффициента поглощения водяного пара методом ТГц-спектроскопии при использовании волноводов типа 1 (а) и типа 2 (б). Серая кривая – точная функция k ( f ), черные колеблющиеся кривые – её восстановление на основании (14)

Колебания восстановленных функций объясняются неполным совпадением производных ∂β v / ∂ n при различных v в (16) и отклонением этих производных от 1. Согласно рис. 3 а, б данные расхождения сильнее выражены для мод волновода 1, с чем связана более низкая точность восстановления k ( f ) на рис. 6 а по сравнению с рис. 6 б . Для количественной иллюстрации этого факта мы рассчитали среднеквадратичное расхождение σ ( k ) между точной и восстановленной функциями k ( f ). Рис. 6 а соответствует σ ( k ) = 1,14 ⋅ 10^–6, а рис. 6 б – σ ( k ) = 3,99 ⋅ 10^–7.

Заметим, что увеличение точности восстановления k ( f ) с ростом частоты для волновода типа 2 связано с отмечавшимся выше квазиодномодовым режимом его работы при f >0,8 ТГц (рис. 3 в ).

Заключение

Разработана техника расчёта широкополосных ТГц-импульсов в протяжённых волноводах, в которой поле импульса представляется в виде суперпозиции импульсов полей отдельных волноводных мод, найденных интегрированием монохроматических компонент. Исследованы капиллярные волноводы с металлизацией внешней границы, обладающие цилиндрической симметрией. Рассмотрены два типа волноводов: полые волноводы и волноводы, полая сердцевина которых отделена от металла диэлектрическим слоем. Для волноводов с диаметром сечения 3 мм, серебряным покрытием и полипропиленовым диэлектрическим слоем определены оптимальные радиусы Гауссова пучка, задающего пространственное распределение возбуждающего волноводы импульса, при которых коэффициенты передачи энергии импульса достигают максимумов, и на примере восстановления спектра поглощения водяного пара оценены возможности терагерцовой спектроскопии воздуха, находящегося в полых сердцевинах волноводов. Волновод с диэлектрическим слоем оказался более эффективным для рассмотренных применений ввиду квазиодномодового режима его работы.

Авторы благодарны М.М. Назарову за полезные обсуждения.

Работа выполнена при поддержке Белорусского республиканского фонда фундаментальных исследований (грант Ф16Р-138).