Распространение упругих волн через периодическую систему трещин в низкочастотном режиме

Введение. Исследование проникновения упругих волн через периодические решетки является важной проблемой в области ультразвуковой количественной оценки материалов, распространении звука и для электромагнитных волноводов с диафрагмами. Различные численные методы были применены в двумерных задачах с периодическими отверстиями произвольной формы [1–3]. Результаты компьютерного моделирования продемонстрировали высокую точность. При этом развиваются и аналитические теории. На практике некоторые приближенные результаты можно установить в аналитической форме в предположении режима низких частот при слабом взаимодействии волн. Таким образом, аналитические методы, обеспечивающие явные формулы для соответствующих параметров рассеяния, задают только определенный низкочастотный предел. В работах [4–7] получены явные аналитические формулы:

• —    для параметров отражения и прохождения в режиме одной моды акустической волны, проникающей сквозь двояко-, троякопериодические массивы отверстий и объемных препятствий произвольной формы;

• —    для плоских задач распространения волн через периодический массив трещин в упругих твердых телах [8].

Случаи высокочастотной дифракции на трещине анализировались в [9–11].

В данной работе изучаются три массива, каждый из которых представляет собой периодическую систему трещин в двумерной постановке. Как показано в [12], качественные свойства такой геометрии аналогичны соответствующей плоской задаче для двух массивов. Предполагается, что при нормальном падении волны имеет место режим распространения одной моды, т. е. ak ₂<  π , где k ₂ — волновое число поперечной волны e ^{ik 1 x} , 2 a — период данной системы. А также расстояние d является таким, что выполняется условие d / a >> 1.

Целью настоящей работы является обобщение результатов, полученных ранее в [12, 13], и вывод новых аналитических выражений коэффициентов для системы трех параллельных экранов (с учетом свойств ядра гиперсингулярного интегрального уравнения). Соответствующие вычисления основываются на решении плоской задачи распространения волны в упругом теле с периодическим массивом трещин.

Постановка задачи. Вывод интегральных уравнений. Рассмотрим структуру, состоящую из трех бесконечных массивов коллинеарных трещин, вертикально расположенных в x =0; d ;2 d . Каждая из трещин, длина которой 2 b , расположена с периодичностью 2 a по оси y . При изучении падения плоской продольной волны e ^{ik 1 x} на данную систему вдоль положительного направления оси x , в силу симметрии вопрос сводится к рассмотрению волновода ширины 2 a (рис. 1).

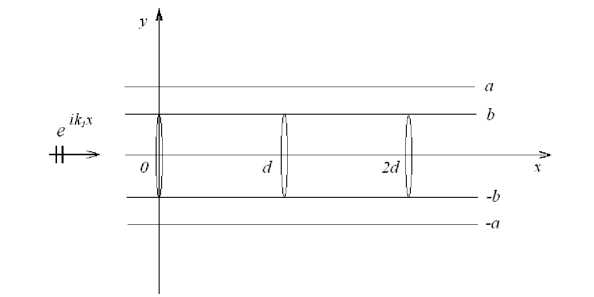
Рис. 1. Фрагмент периодического массива трещин

Fig. 1. Segment of periodic array of cracks

Тогда потенциалы, удовлетворяющие уравнению Гельмгольца, есть функции: ikx      - ikx   ” . q_x      П ny фleft = e 1 + Re 1 + ЕAne n coslI n=1

Vet = ЕBneV sin f^nyI, x < 0; n=1

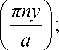
^{ф s} = e kx + F 0s ^cos [ k 1 ( x _ x s -1 )] + H 0s c° ^s [ ^k 1 ( x - x s )] + Е ^{ F^ch [ q n ( ^x - x s -1 )] + H n ^ch [ q n ( ^x - x s ^)]}cos n =1

Vs = ЕЕ {GSch[rn (X - Xs-1)] + Pnch[rn (x - xs )]}sin fnny|, (s-1)d < x < sd; s = 1,2; n=1

п пу

a

ф right = Te- Ik ^{1 [} x ^{- 2} d ^] + Е C n e ^- qn ^[ x ^{- 2} d ^] cos n =1

Vright = Е Dne"rn[x-2d] sinfпnУI x > 2d.(1)

n=1

Заглавные буквы здесь являются неизвестными константами, а 1/21/2

qn = [(Пn / a)- k2 J , rn = [(Пn / a)- k2 J -

Гармонический временной множитель берется в виде e ^- i ™ t , k 1, к ₂ являются продольным и поперечным волновыми числами, а R , T — коэффициенты отражения и прохождения соответственно. Далее возьмем компоненты тензора напряжений ст _xx ; ст _x y и вектора перемещений u_x , u y в терминах потенциалов, используя стандартные формулы Грина — Ламе. В рассматриваемой задаче плоская продольная волна с потенциалами ф₀ = e i¹ x , v ₀ = 0 приходит из -да и порождает отраженное поле. Предполагая непрерывность поля перемещений вне трещин, введем следующий вектор неизвестных функций g x ( у ), g y ( у ), | у |< b :

u ^{( left} ) - u ⁽¹⁾ = g 1 ( у ), x = 0; u ⁽¹⁾ - u ⁽²⁾ = g ² ( у ), x = d ; u ⁽²⁾ - u ^{( rlght ) =} g ³ ( у ), x = 2 d .                 (3)

Используя (1)—(3), найдем все необходимых постоянные, входящие в потенциалы (1), через gx (у), gy (у). Для этого сначала проинтегрируем уравнения (3) по отрезку | у |< a , чтобы получить систему для 6 коэффициентов, не входящих под знак суммы в выражениях для потенциалов:

1 ^ь

^- i^k 1 ^{R -} H 0 ^k 1 ^{sin( к} 1 ^d ) = — J g x ⁽ у)^dy ;

2 a - ь

1                        2                        ¹ b 2

^- F 0 ^к 1 ^{sin( к} 1 ^d ) ^- H 0 ^к 1 ^{sin( к} 1 ^d ) = ^- J g x ⁽ у W ^;

2 a - ь

- F 0² к 1 sin( к 1 d ) + ik 1 e ik ¹² d - ikT = ;1 b g x ( у)dy .                                    (4)

2 a - ь

Свойство ортогональности тригонометрических функций с учетом предположений метода q_nd >> 1, n = 1,2,3... приведет (3) к соотношениям, связывающим остальные 12 коэффициентов:

^[ A n + H n sh ⁽ q n d ^)] q n + ^[ B n ^- P ^{1 ch (} r n d ) D n 3^)] ^ n = 2¹ J g x ⁽ у ^)cos Р^{п пу} | ^dy ;

a 2 a - ьV

^{[ -} A n + H n ch ⁽ q n d ^)]— ^{- [} B n + P n ^{sh ( r} n d ^{)] r} n =;¹ J g у ⁽ у ^{)sin f ппу} | ^dy ;

a                        2 a - ьV

^[ F n + H ^2] q n ^{sh (} q n d )+ ^[ G n ^- P ,^{2] n}n^ch ^{( r} n d ) = v- J g 2 ⁽ у ^{)cos f ппу} | ^dy ;

a 2 a - ьV

^{[ -} F n + H n ^{2 ] n}n^{ch (} q n d ) ^{- [} G n + P ,^{2] r} n ^{sh ( r} n d       J g y ⁽ у ^{)sin f ппу} I ^dy ;

a                               2 a - V a )

[ F n² sh ( q n d ) + C n ] q n -

^[ Gch ⁽ r n d ) ^- D n ^]— J J g X ⁽ y ^)cos 2 a - b

a

;

^{[ -} F 2 ch ⁽ q n d ) + C n ^]—^- a

1 b

^[ G n sh ⁽ rd ) + D n ] r n =    J g y ⁽ y ) ^sin

2 a - b

Условия непрерывности напряжений на границе имеют место в виде

( left ) ₌ (1).    ( left ) ₌ (1)         ₀ . (1) ₌ (2). (1) ₌ (2) _d . (2) ₌ ( right ). (2) ₌ ( right )

^и xx     ^и xx ; ^и xy ^и xy , ^{x o} ; ^и xx   ^и xx ; ^и xy   ^и xy , ^x d ; ^и xx ^и xx ; ^и xy ^и xy , ^{x   2} d ^.

После применения для (6) аналогичной процедуры интегрирования по отрезку и принимая во внимание свойство ортогональности тригонометрической функции, получим остальные 9 соотношений, которые вместе с (4) и (5) образуют алгебраическую систему с 18 неизвестными постоянными задачи. Часть решения системы, соответствующая x = 0, определяет постоянные Р П , A n , B n , H n¹ , F _o ⁽¹⁾ , H 01) , R , выражения которых, используемые ниже, принимают вид:

ik d e 1 b

F o =----------- J g x (n) d n -

4 ak 1 sin( k 1 d ) _ _b

b

g ² (n) d n 4 ak 1 sin( k 1 d ) - b

^^^^^в

ik d e ^{1 b} --------------J g 3 (n) d n; 4 ak 1 sin( k 1 d ) - b

H0 =

^^^^^^в

h n

b

g ¹ (n) d n + 4 ak 1 sin( k 1 d ) - b

ik,d                                  ik 2 d e 1 b                       e 1 b л

-------------J g ²(n) d n +------------- I g 3 (n) d n;

4 ak 1 sin( k 1 d ) - b            4 ak 1 sin( k 1 d ) - b

1 b .

R = ^-       J g x ⁽ n ^{) d} n

4 ak 1 i _ b

^^^^^^в

ik'd ,                     ik 2d , e 1 b e 1 b -77-. J gx(n)dn-—— J gx(n)dn; 4 ak1 i _b             4 ak1 i _ b

^^^^^^в

2 .   2

r j + a n

² ash ⁽ q n d )     q_nk ₂ ²

b          f nnn) , 2 a„ b          f nnn)

J g x (n)cosl      I d n+ n J g y (n)sinl      I d n];

- b          I a J k 2 - b          I a J

2     2

1 r_n / + a „ A =— [- -j. n n ² a q n k 22

b       fnnnVJ gx (n)cosl      I dn-

- b

a

2 a„ b          fnnn)

-y J gy(n)sinl      Idn];

k ₂ ² - b          I a J

' 2

R = 1 Г2 an b

^B n ^{[ J}

2 a k 2 - b

^^^^^^в

Y o

2 , 2 c 1 r n ^k 1

b 1        fnnn)

J g y (n)sinl       I d n];

1 a )

- b

J _ 1 2 ash ( q_nd )

2an b 1/ л fnnnV 77 J gx (n)cosl I dn k22 - b          I a J

^^^^^^в

Y o

2 i 2 c 1 r n ^k 1

b 1 fnn n)

J g y (n)sinl       I d n].

- b I a J

Формулы для остальных постоянных для краткости опускаем.

Теперь полученные постоянные используются для удовлетворения условий равенства нулю компонент тензора напряжений на трещине. Здесь следует принять во внимание, что в задаче остаются только нетривиальные функции раскрытия g xs ( y ); | y |< b ; s = 1,2,3 , учитываемые в соотношениях

• ( left ) _{= n}(1) -0   _{r =} 0 • _п(1) = П⁽²⁾ - 0     x-d • r>⁽²⁾ = (ri right ) - 0

xx ^a xx = ⁰ ,   ^{x 0} ; ^a xx ^a xx = ⁰ ,    ^x = d ; ^a xx ^a xx    = ⁰ ,

x = 2 d .

Опуская промежуточные преобразования, окончательно получаем следующую систему трех интегральных уравнений относительно функций g x ( y ); | y |< b ; s = 1,2,3 :

1 b

— J K ⁽ y ^- t ) g X ⁽ t dt ⁺ 2 a - b

ik d                   ik 2 d e 1 b e 1 b

-туг J g 2 ⁽ t ) dt ⁺тут J g 3⁽ t ) dt = 1;

4 ak 1 1 _ b            4 ak 1 г _ b

ik d e 1

b

4 ak 1 i - _b

- 1              1 b 2

J g X ⁽ td ^-— J K ⁽ y ^- t ) g 2⁽ t ) ^{dt +} ,            2 a _ b

ik d e b ikd

J g x ( t ) ^dt = e ¹ ; 4 ak 1 1 _ _b

ik 2 d e ¹ b

J g 2⁽ t ) ^{dt +} 4 ak 1 i - _b

ik d e ¹

b

1 ^b

. . . J g x ⁽ tdt ^-— f K ⁽ y ^- t ) g 3⁽ td = ^e

4 ak 1 1 - b          2 a - b

ik 2 d

где K ⁽ y ^)_ i ^{/2 k} 1 + £ ⁽ R n I q n k 2^{2 )cos( n}ny I ^a X R n = ^[2 a n ^{- k} 2^{]2 - 4} r n q n a ^2, a n = ⁿⁿ / a .

n =1

Свойства интегрального уравнения. Начнем с рассмотрения вспомогательного интегрального уравнения:

• 1    b                                                  да                                 R„. .

  
  

— J h (n) K ( У -n) d П = 1; K ( У ) = Z L n COS( a n y ); L n = -y—, I У l< ^b .

• ^{2    a} - ь                                  n =1

Заметим, что L n —2(1 - c 2 / c ² ) a n , n ^ да. Тогда выражение ядра преобразуется к виду:

I       c  1 да                           да               I       c    1                                                   I       c1

K ⁽ У ) = ^{- 2} | 1-- 2 | Z ^a n ^cos( a n y ) + Z L n + ² | ¹--2 I a n ^cos( a n y ),     K ⁽ y ) = ^-2M-- 2 I I ⁽ y ) + K r ⁽ y ).

k   c1 Jn=              n=        k   c1 J                              k   c1

Здесь вторая сумма ядра есть некоторая регулярная функция. Первая имеет как регулярную, так и сингулярную части: I(у) = [Ir (у) + Is (у)], для выделения которых рассмотрим выражение да

-I ( У )= Z n cos( — у ).

п         n =1         a

Используя обобщенное представление да       /Пn             да _Е„      ,пn .               1

Z n cos(— у) = lim s e n cos(— y) =----------, n=1       a      E^+0 n=1           a         4sin2(nу /2 a)

для суммы (11), имеем преобразование a a

(---——, у ^ 0), после чего ядро вспомогательного п ² у

интегрального уравнения (10) представляется в виде: K(у) = -2(1 -c2/c2)[Ir(у) + Is(у)] + Kr(у), где сингулярная и a aπ регулярная части есть соответственно Is (у) =---, Ir (у) =---------------.

п у п у   4 a sin ² ( пу /2 a )

Легко видеть, что особенность ядра для малых аргументов содержит гиперсингулярность по одной переменной, возникающую в теории трещин, хорошо известную в задачах теории упругости в неограниченных средах [14]. Для устойчивости численного метода при выполнении расчетных экспериментов здесь применяется дискретная квадратурная формула для гиперсингулярных одномерных ядер, известная как «метод дискретных вихрей» [15]. Используя новое представление ядра основного интегрального уравнения (10), перепишем его следующим образом:

2 a [1 - c | ] c 2 ^Ф r ⁽ у ^-n)⁺—----;r

^{П (} У ^- n)

1 b

J h ⁽ n) ^{2 a} - b

d n = 1, Ф r ( у ) = -2[1 - -f] I r ( у ) + K r ( у ).                     (12)

c 1²

Дискретизация интегрального соотношения (12) приводит к формуле

1 N П к

— Z J h ⁽ п) ^{2 a к} =1П к - 1

2 a [1 - c | ] c ²

^Ф r ⁽ У / ^- П )⁺ —------у

^{П (} У / ^- n)

1 N       П к dn= Z h (nк) J h (n)

^{2 a к} =1       П к - 1

2 a [1 - c | ]

c ²

^Ф r ⁽ У / ^- n к )£ 1 ⁺ —----- -у d ⁽ П ^- У / )

п( У / -П) ²

Г                Л         Л 1 N = v Z h (Пк) 2a к =1 2 a[1 - -2]     2 a [1 - -2] - , х                     c1                        c1 Ф r(у/  Пк )£1 +        „ '              ч П(У/ -Пк)    П(У/ -Пк -1) [                                                   ] где пк = -b + к£j, y/ = -b + (/ -0,5)£j , I = 1,...,N , £1 = 2b/ N .

В итоге имеем алгебраическую систему уравнений:

N

— Z h (П к ) 2 a к =1

2 a [1 - c | ]

^Ф r ^{( у} / ^-П к ^{) £} 1 ⁺

⁽ У / ^- П к )

^{( у} / ^{- П} к -1 )

= 1.

Аналитические выражения волновых характеристик. Используя вспомогательное уравнение, входящее в (10), для решения которого вводится постоянная

b

H =J h ( t ) dt ,                                                 (13)

-b в терминах функции h(у) из (9) и (10) получаем:

k 22 g 1 (П) = h (П)[(1/ 4 aik 1 ) J i + ( e ik ¹ d / 4 aik 1 ) J ₂ + ( e ik ¹2 d / 4 ak ) J ₃ — 1];

k 2 2 g 1 (П) = h (П)[(1/ 4 aik 1 ) J ₂ + ( e ik ¹ d / 4 aik 1 )[ J 1 + J ₃] — e ik ¹ d ];

k 2 2 g 1 (П) = h (П)[(1/ 4 aik 1 ) J ₃ + ( e ik ¹ d /4 aik 1 ) J ₂ + ( e ik ¹2 d /4 aik 1 ) J 1 — e ik ¹2 d ],

где обозначено

b

J j =f g j (t)dt , j = 1,2,3.

- b

После интегрирования уравнения (14) по множеству | y |< b с учетом (13) получаем систему линейных алгебраических уравнений относительно J j , j = 1,2,3 :

( k ₂ ^{- 2} -H / 4 aik₁ ) J 1 - ( He ik ¹ d / 4 aik₁ ) J ₂ - ( e ik ¹2 d H / 4 aik₁ ) J ₃ = - H ;

-( He ik ¹ d / 4 aik 1 ) J 1 + ( k ₂ ² - H / 4 aik 1 ) J ₂ - ( e ik ¹ d H / 4 aik 1 ) J ₃ = - He ik ^{1 d} ;

-( He ik ¹2 d / 4 aik 1 ) J 1 - ( e ik ¹ d H / 4 aik 1 ) J ₂ + ( k ₂ ² - H / 4 aik 1 ) J ₃ = - He ik ¹2^d

После того как найдено решение системы (16), т. е. найдены величины J j , j = 1,2,3 и параметр H , находим все необходимые волновые характеристики. В частности, коэффициенты отражения и преломления будут выражены в виде:

ik d e1b

—— f g i ⁽ t ) ^{dt -} 4 aik 1 - ь

ik 2d e1b

-r-r f g1 ⁽ t ) dt ;

4 aik ^ _ ь

1 ^b 1

R = ^-7—Г f g i ⁽ t ) ^{dt -}

4 aik1 - ь ik 2d 1b

T = -f g 1 ( t )d 4 aik y _ ь

ik d e ^{1 b} TT f g i ⁽ t ) ^dt 4 aik ^ _ ь

1 ^bik 2 d

—— f g 1 ( t )dt + e *

4 aik ^ _ ь

Отметим, что данная теория позволяет найти коэффициенты (17) в явном виде, а единственным вопросом, который решается здесь численно, является построение решения основного вспомогательного гиперсингулярного интегрального уравнения (13). Исходя из этого, предлагаемый метод может быть назван «полуаналитическим».

Обсуждение и результаты. На рис. 2–5 продемонстрированы некоторые примеры зависимости физических параметров от частотного параметра ak / п , ( k = к 2 ) и длины трещины в упругой среде с отношением упругих скоростей c 1 / c ₂ = 1,87 . Модуль коэффициента прохождения | T | с ростом частоты после нескольких осцилляций всегда уменьшается, независимо от геометрии решетки. Осциллирующий режим и одновременно определенные потери прохождения очевидны при увеличении длины трещины b / a (рис. 2).

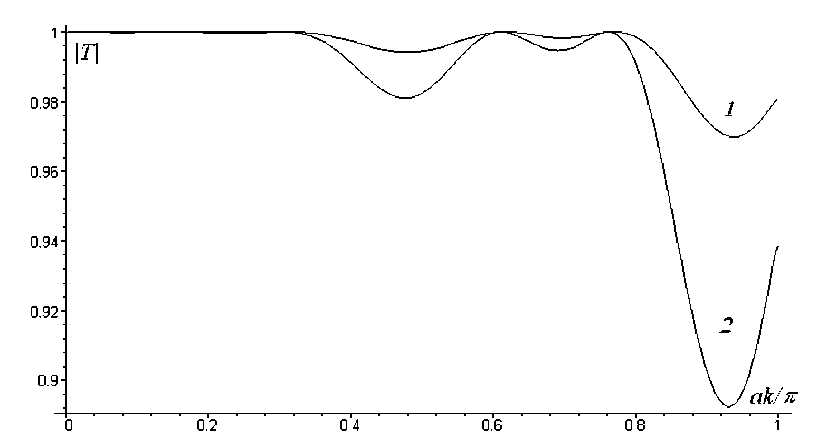
Рис. 2. Зависимость коэффициента прохождения от частоты: a = 1; d = 4; кривая 1 — b / a = 0,15; кривая 2 — b / a = 0,2

Fig. 2. Dependence of transmission coefficient on frequency: a = 1; d = 4; curve 1 — b / a = 0,15; curve 2 — b / a = 0,2

При фиксированных ak ₂ / π и d модуль коэффициента отражения | R | при изменении параметра b / a может иметь различный характер поведения (рис. 3).

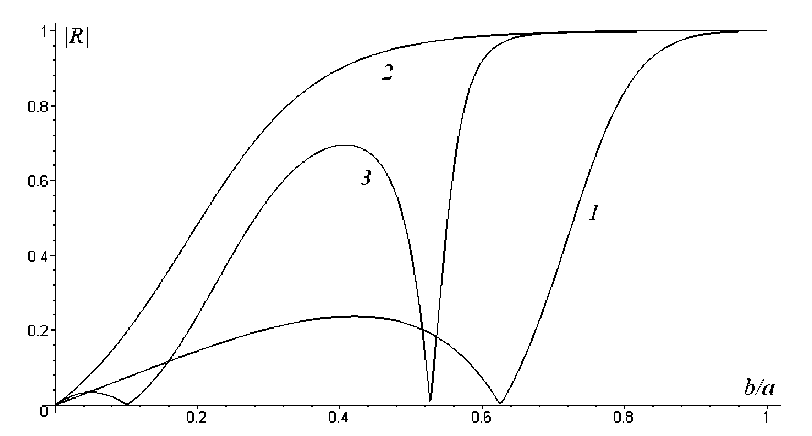
Рис. 3. Зависимость коэффициента отражения от длины трещины:

a =1; d =4; кривая 1 — ak ₂ = 0, 222; кривая 2 — ak ₂ = 0, 357 ; кривая 3 — ak ₂ / π = 0, 595

Fig. 3. Dependence of reflection coefficient on crack’s length:

a =1; d =4; curve 1 — ak ₂ = 0, 222; curve 2 — ak ₂ = 0, 357 ; curve 3 — ak ₂ / π = 0, 595

Для одних частот это монотонно возрастающая функция на всем диапазоне изменения величины трещины (кривая 2). В других случаях при некотором размере трещины достигается локальный минимум (кривая 1) или даже несколько локальных минимумов (как на кривой 3). При некоторых размерах трещины может происходить полное запирание канала, когда | T |= 1. Если d и ak ₂ / π зафиксированы, то максимальное отражение наступает для наибольшей трещины в материале. И наоборот, слабое отражение происходит для небольших трещин, что вполне естественно с физической точки зрения.

Также отметим, что для заданных b / a и ak ₂ / π величина | T ( d )| может достигать минимума. При этом имеются такие значения d , для которых достигается полное прохождение (рис. 4).

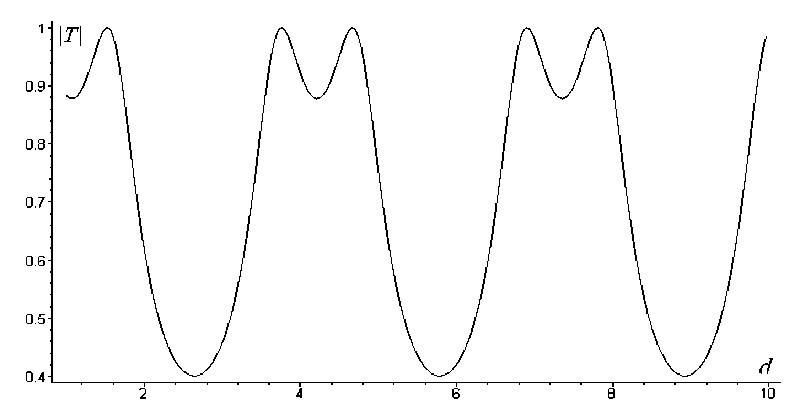
Рис. 4. Зависимость коэффициента прохождения от расстояния d ; b / a = 0,45; ak ₂ = 1,87

Fig. 4. Dependence of transmission coefficient on distance d ; b / a = 0,45; ak ₂ = 1,87

На рис. 5 показано, что свойство акустических фильтров достигается не только для относительно длинных трещин, что вполне естественно, но также и при средней их длине.

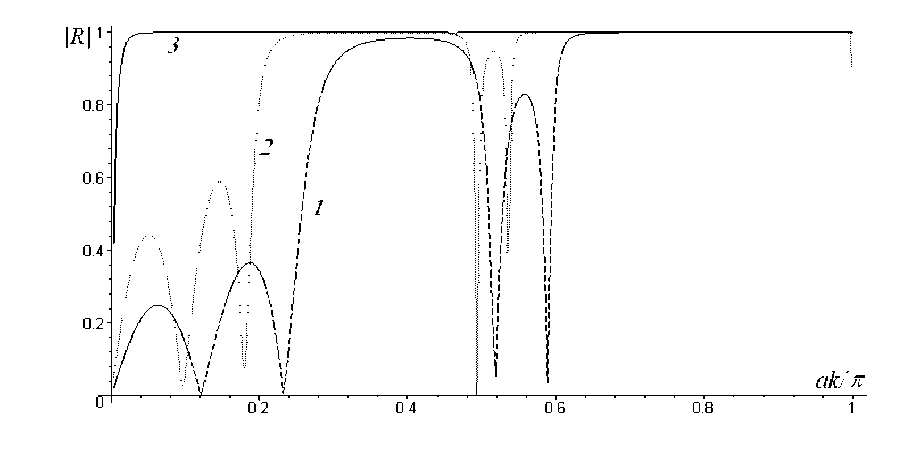
Рис. 5. Зависимость коэффициента отражения от частоты: a = 1; d = 4; Кривая 1 — b / a = 0,7; кривая 2 — b / a = 0,9; кривая 3 — b / a = 1 Fig. 5. Dependence of reflection coefficient on frequency: a = 1; d = 4; curve 1— b / a = 0,7; curve 2 — b / a = 0,9; curve 3 — b / a = 1

Кривая 3 для максимально длинной трещины подтверждает правильность настоящего расчета при анализе предельного случая, когда значение функции отражения становится постоянным почти на всем одномодовом частотном интервале, что вполне естественно. В самом деле, для любой геометрии в случае крайне низких частот коэффициент отражения начинает расти от нулевого значения. С другой стороны, для любой фиксированной частоты, | R |^ 1, когда b / a ^ 1. Поэтому для больших трещин возрастание | R | от нуля до единицы должно происходить в начале одномодоваго интервала по частоте. Однако интересно также, что уже для среднего размера трещины (кривая 1, b / a = 0,7;) имеется пара относительно длительных частотных интервалов, где коэффициент отражения приближается к единице, при этом существуют такие частоты, при которых запирание волны резко меняется на почти полное ее пропускание. Вообще же свойство фильтра на верхних частотах данного одномодового интервала имеет место для всех представленных значений длины b / a .

Выводы. Специфика внутренней структуры в рассмотренной задаче позволяет достичь свойств акустических фильтров за счет выбора частоты, расстояния между периодическими массивами трещин, а также длины имеющейся здесь периодической неоднородности. Метод, развитый в настоящей работе, может эффективно применяться в исследовании и более сложных трехмерных волновых задач, когда вертикальный массив, содержащий двухпериодическую систему трещин, последовательно повторяется периодически конечное число раз вдоль направления распространения волны. Троякопериодическая система будет предметом следующей работы, в которой предполагается рассмотреть некоторые новые специфические свойства волн в упругих средах, не наблюдавшиеся при исследовании аналогичных задач в скалярной постановке.

Автор выражает благодарность заведующему кафедрой теоретической и компьютерной гидроаэродинамики Института математики, механики и компьютерных наук ЮФУ профессору М. А. Сумбатяну за внимание к работе и ценные замечания при подготовке публикации.