Распространение упругих волн в трехмерном слое в зависимости от моделей пластины

1. Введение. В работах [1-3] для акустического и изотропного слоев изложен метод решения задачи для определения асимптотических полей в случае действия на поверхности трехмерного слоя осциллирующей нагрузки, расположенной в произвольной области. Главные члены асимптотики были получены в случае действия нагрузки в прямоугольнике и по линии [4, 5]. В данной работе исследуются три известные модели для поперечных колебаний пластины [6], лежащей без отрыва и трения на трехмерном изотропном слое.

На поверхности пластины осциллирует нагрузка, заданная в произвольной области. Изучается влияние на асимптотическое распространение волн в слое различных моделей пластины: с учетом сдвига (пластина ПС), с учетом момента инерции (пластина ПИ) и с учетом этих двух факторов (пластина ПСИ).

2. Постановка задачи. Уточненное уравнение поперечных колебаний пластины ПСИ, учитывающее влияние инерции вращения и деформации поперечного сдвига имеет вид [6]:

+ — V 2 V ² S t p h

—

_D_+1   v 2+ k2 p h h ) dt2     k2 p h dt4

Г V =

f 1. I d ²       D     2 ,2 L / A / ЛА

--—з —у—,—7----- V Г ( p ( x,y,t )— q ( x,y,t ) ) p h  k ² p h ² d t ²   k ² pp h ²²

Из уравнения (1) вытекают как частные случаи уравнение колебаний пластины ПС

< DV ² V ²

p D d ² k ² p dt²

V² + p h ^-r >

² dt ²

V =

P , 2    ,^{V 2} r ( p ( x , y,t )^— q ( x , y , t ) )

■h

—

и уравнение для пластины ПИ

< DV ²V ²

— pI ^V ² + ph

²   dt^{2          2}   dt²

Г v =

p ( x, y, t ) — q ( x, y, t ) .

Уравнения колебаний слоя имеют вид:

(^ + p1) (divu ),k +p1 Auk = p1 uk, k = 1,2,3, где Х1, pi, pi, Н, Xi, р2, р2, h, V2 - постоянные, соответственно характеризующие слой и пластину, А - оператор Лапласа в трехмерной области, А2 - квадрат оператора Лапласа в двумерной области ху, D = ( ^2h3)/(6 (1 -v2)), v2V2 = d, + d , + 2 f . , I = — .

^x '                       d x ⁴    d y ⁴     d x ² d y²      12

Граничные условия и условия сопряжения пластины и слоя имеют вид

Р ( ~ ,у , t ) =

' f (x , y V ^Q , ( x , y ) e 5 , . 0, ( x ,y ) ^ 5,

q ( x,y , t ) = < 7 -33 ( x,y , H , t ) , v ( x , y , t ) = u 3 ( x , y , H , t ) , a _k 3 ( x,y , H , t ) = 0, k = 1,2

7 3 ( x , y ,0, t ) = 0, k = 1,2 , u 3 ( x ,y ,0, t ) = 0 ,          (3)

где S - некоторая ограниченная область с кусочно-гладкой границей.

Далее рассматривается установившийся режим колебаний, т.е. решение системы ищем в виде

('(_,-_,-_      ~rk~        /о/                 ~/~ x,y,z,t) = U(x,y,z)e    , ~3(x,y,t) = V(x,y)e  , аи = <~kte

~

и вводятся безразмерные величины

~

~

xyz

x = —, y = —, z = —, U

H H H -

U

H ’

~

~

V = V,Q = 2H

H

^c 1

,

5 = —

5 H ’

D =--#h-г

6 H ЪР1 - v 2 )

c 2   2 _ ^ 1 ^{+ 2} M 1

, c         , ^c 1

^c 1

P 1

,

c 2

₌ ^ 1 „ ₌ ^ 2. _n =P^_ Ц      , ^P      .

P 1       ^ 1       P 1

При решении задачи будем применять принцип предельного поглощения, который фактически приводит к замене Q на Q _£ = Q - is, 0 <  е << 1, и искать решение в классе функций, убывающих на бесконечности, т.е. u ( x , y , z , t ) ^ 0 , если r = ^x ² + y² ^ да.

Применяя к системе дифференциальных уравнений и условиям (2), (3) преобразование Фурье по координатам x и y , и решая полученную систему уравнений с соответствующими граничными условиями, найдем:

да да

U 1 т е = 7^! I i “ Q m ( “ ' Г ) A ( ^ ^ е , Z ) = -" ' V "'"d a d y , 4 ^

-да -да

1 ^{да да}

U 2 т . = ^J f I iYQ . ( a , Г ) A (^f, ° е , z ) e -"^e -' ^rd ^{a d} / ,

-да -да

1 да да

U...... = 72? II P ' d Q m ( a , Y ) С(‘ ••ⁿ . , z ) e - ^a x ^e -" d a ^ Y ,

-да -да где A (^, Q, z) = -Exs—ec—вz + 2ДДsh^chez , 6(£, Q, z) = Evshe she z - 2^2 sh^ sh^ z

Окончательное решение рассматриваемой краевой задачи получим с помощью предельного перехода [7]: lim U = U.

e ^0 — ^s

Выражения для контактных напряжений, преобразованных по Фурье, Q ( a, у ) для трех рассматриваемых моделей, выраженные через заданную нагрузку, также преобразованную по Фурье, имеют вид:

Qm (а, у) = A(£,Q)Km (£,Q)F(a, y)/Aт (£, Q), m=6,7,8,где €2 = а2 + у2,

I Q ²

,         .           ,         . I 1

A₆ (Q Q) = A( £, Q) —   _{7  7 7}

6V   ’   V   \p£ k1^1?

—

D2 k ' p

+

+вshe she (E\ — 2^2)

A₇( £, Q ) = A ( £ , Q ) 1

—

Dс2 4

P^

—

I pQ4 k2 p<;c2

D

—

,

D2

k u.

+ в sh e sh e ( E i — ²^2 ) D^ ⁴ +

pQ ( D£2

с ²

k ² Ц

—

A8 (£, Q) = A (£, Q) + вshp shp (Ex — 2^2) I D£4 — pQ- (112 + ^) ,               c

A(£, Q) = E2chpshe — 4eppshpchp,

K 6 ⁽^, ^Q) = p^ - k^;^ ’ ^K 7 ⁽', ^{Q )} = ^{1 —} k 2 4^ ’ K 8 ⁽", ^{Q )} = ¹

• 3.    Численное исследование дисперсионных уравнений. В работе [8] на основе численного анализа показано, что более существенное влияние на распространение потока энергии в слое, укрепленном пластиной без учета сдвига и инерции, оказывает увеличение плотности пластины по сравнению со слоем, чем изменение отношения их жесткостей. В данной работе численные исследования уравнений (4)-(6) показали, что дисперсионные кривые для слоя, укрепленного пластиной, тем сильнее отличаются от дисперсионных кривых для одного изотропного слоя, чем более плотным является материал пластины по сравнению с материалом слоя, и чем больше толщина пластины. При исследовании трех различных моделей пластин выявлено, что все модели пластин дают

  одинаковый результат до Q=Q o для первой дисперсионной кривой, свыше Q o дисперсионные кривые расходятся, что видно из рисунка. В качестве материала слоя выбран плавленый кварц, а материал пластины - вольфрам: р=2,609, р=3,858, ^=0,1. В этом случае Q o -0,8. Если перейти к размерным переменным, получим, например, что при толщине слоя Н=100м частота колебаний Q о ~О,О42 Гц, а если Н=10м, то Q 0 -0,0042 Гц. На рисунке приведены графики дисперсионных кривых для изотропного слоя (сплошные линии), для изотропного слоя, подкрепленного пластиной ПИ (мелкий пунктир) и пластиной ПСИ (крупный пунктир), коэффициент k = 5^66 = 0.913 .

• 4 .    Заключение. В работе рассмотрены три модели пластин, лежащих без трения и отрыва на упругом трехмерном слое, и выяснено влияние различных моделей на асимптотическое распространение волн в слое при действии нагрузки в произвольной области S .

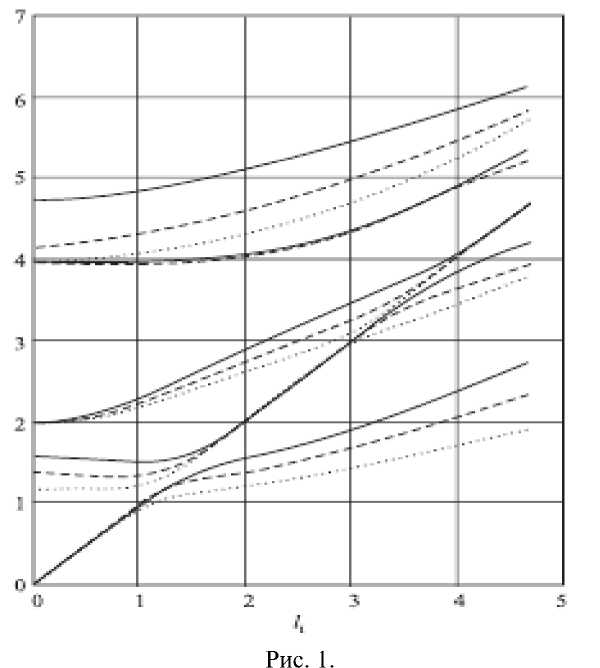
Дисперсионные кривые, когда рассматриваем модель пластины ПС, при таких же значениях параметров примерно совпадают с дисперсионными кривыми для пластины ПИ.

Конкретные расчеты, проведенные для различных областей показали, что все модели пластин дают одинаковые первые дисперсионные кривые до Ω=Ω 0 , свыше Ω 0 дисперсионные кривые расходятся.

Сравнение результатов, полученных для слоя и слоя с различными моделями пластин, показало, что наиболее близкой к одному слою является модель для слоя с пластиной ПСИ, следовательно при расчетах нужно использовать модель слоя с пластиной ПСИ.