Распространение волн в трехкомпонентных слоистых фононных кристаллах

Исследование распространения волн в различных средах началось еще в 17-м веке и продолжается и по сей день. Анализ этих явлений является важным инструментом для решения прикладных задач, связанных с неоднородными одномерными периодическими структурами. Среди сред, в которых акустические волны могут распространяться, можно выделить такие часто встречающиеся структуры, как пузырьки газа в жидкости, пенные материалы, смеси с периодически изменяющимися компонентами, разнообразные композиты, зернистые и пористые структуры, и другие подобные. То же самое относится и к электромагнитным волнам.

Структура «кварц-вода-воздух», исследуемая в данной работе, может служить примером пористого нефтяного или заводненного пласта. В рамках прикладных задач имеет важное значение определение полос пропускания и полос запирания, а также акустическое зондирование, позволяющее находить значения линейных концентраций на основе заданных фазовых скоростей. Кроме того, исследование свойств замедления в неоднородных од- номерно-периодических структурах имеет важное практическое применение.

Данная работа берет свое начало в статьях С.В. Сухинина в области исследования акустики неоднородных сред. В данной работе [1,4] были использованы как основополагающие источники. В [2, 3] содержатся результаты первоначальных исследований, а также приведена библиография. В нашем исследовании, изложенном в работе [4], был проведен анализ характеристик волноводов и резонансных свойств гетерогенных проницаемых одномерно-периодических структур, состоящих из двух различных материалов, с использованием одномерного приближения. В результате исследования были выявлены полосы пропускания и полосы запирания, а также получено дисперсионное соотношение, описывающее характер волноводных моделей. Для моно- и полидисперс-ных сред были найдены четкие выражения для низких волноводных частот и соответствующих фазовых скоростей волноводных моделей. Существует несколько исследований, показывающих, что гетерогенные многокомпонентные композиты могут иметь многообещающие виброизолирующие и звукопоглощающие свойства (см., например, [5]). Основываясь на результатах работ [6, 7], виброизоляция и эффективность защиты звука иллюстрируется путем изучения распространения волны в пористой среде заполненный жидкостью и газом.

Исследования, проведенные в данной работе, можно сказать, что обобщают результаты вышеуказанных работ. Особенность изучения трёхкомпонентной среды -увеличение вычислительной трудности, т.к. с ростом количества границ между средами фундаментальной ячейки увеличивается и количество уравнений, и количество свободных параметров. Как цель текущей работы рассматривается исследовать свойства трёхкомпонентной структуры неоднородностей и решить обратную задачу нахождения концентрация компонентов по измеренным значениям фазовых скоростей. Результаты исследования могут быть использованы для получения новых композиционных материалов, звукоизоляционных фильтров, улучшению демпфирующих устройств и материалов.

Модель и свойства симметрии

В распространении волн в одномерных периодических структурах существует важное свойство: волной считается фазовое распространение колебаний в фундаментальных ячейках. Однако из-за большого числа неоднородностей возникают значительные трудности, которые делают невозможным использование прямых методов для изучения распространения волн в таких неоднородных периодических структурах. Поэтому анализ структуры частотного спектра в задаче, описывающей колебания в одномерно-периодических структурах, приобретает важное значение и становится ключевым аспектом исследований.

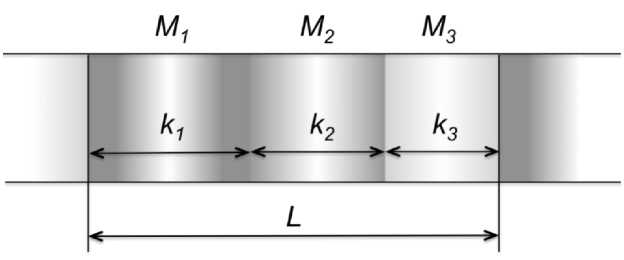
Рис. 1. Монодисперсная цепочка неоднородностей

Пусть одномерная периодическая среда (гетерогенная), представленная на рисунке 1, составлена их трёх сред - М1 = { c1,p1}, М2 = { c2,P2} и Мз={ Сз,рз}, где pi-плотность среды, ci – скорость звука при покое. Допустим, что цепочка неоднородностей, состоящей из компонентов М1и М2, заполняет компонент М3 (матрица композита), а линейная концентрация связанных слоев компонентов равна к1, к2 и к3 соответственно, причем считаем, что к1 + к2 + к3 = 1. Индексы i = 1, 2, 3 соответствуют средам М1, М2, М3 соответственно. В дальнейшем предполагаем, что плотности сред удовлетворяют соотношению Pi > р2 > р3. Эта цепочка является пространственно-периодической, в которой наименьший пространственный пери- од равен L. Будет рассматриваться безраз-л мерную переменную по пространству х = x/L, в дальнейших рассуждениях крышку опустим для простоты описания. Используя такие обозначения получаем, что наименьший пространственный период равен 1. Среда, имеющая такую длину, называется фундаментальной ячейкой. Также введем вспомогательные параметры Tij = Pi/Pj, которые будут показателем отношения плотностей для соседних слоев, и Kij = Ci/Cj как отношений скоростей звука в соседних слоях. Стоит отметить, что цепочка, которая состоит из трёх различных сред, имеет свойство пространственной периодичности. Дальнейшие вы- числения проводятся в безразмерных переменных.

Стационарные акустические колебания давления с круговой частотой го в средах

М 1 , M 2 , М з , описываются следующими уравнениями (Гельмгольца):

Р^ + ^2Р(1) = 0^2 + ^2К22Р(2) = 0,р£> + П2К2зр(2> = 0,              (1)

где р⁽¹⁾, р⁽²⁾ и р⁽³⁾ акустические давления в соответствующих компонентах цепочки, го = 2ir f - угловая частота, Q = — - волноводная частота, являющаяся безразмерной ча-

С 1

стотой колебаний. Для каждой из сред имеется общий вид решения, которое может быть выражено следующим образом:

р(1) = d1ein% + b1e ‘п%,р(2) = n2einK12% + b2e inK12% p(3) = a3einKi3% + b3e--YKix

Условия на границе контакта компонентов являются непрерывность давления и скорости (нормальной компоненты) - два типа граничных условий:

р(1) = р(2), р(2) = р(3), р(з) = р(1),

(1) ^ 21 р %

(2) ^ 32 р %

(3) Чзр ^

= р ! ^2> .

= /'Л

= р“-

Указанные выше уравнения (1), (2) и (3), обозначаемые как задача Т, предоставляют полное описание распространения акустических волн в неоднородных одномерно-периодических структурах.

Свойства симметрии. В силу инвариантности волнового уравнения относительно локальных плоских симметрий, симметрия задачи Т идентифицируется симметрией последовательности неоднородностей. По определению, все одномерно-периодические структуры допускают группу {Т}, следовательно пространство допускаемых решений раскладывается на инвариантные подпространства [2]. Так как гетерогенная цепочка неоднородностей имеет свойство пространственной пе- риодичности, её можно отнести к фононным кристаллам (по определению). А как известно, инварианты относительно группы {Т} по пространственной переменной все кристаллографические группы. Соответственно, по свойству коммутативности {Т} получаем, что её любое представление унитарно и одномерно в пространстве допускаемых решений, поэтому можем его разложить на инвариантные одномерные подпространства. Мощность множества инвариантных полученных подпространств бесконечна. Рассматривая свойства симметрии среды, решение задачи удовлетворяет теореме Флоке (условия сдвига фазы колебаний):

р(х + 1) = р(х)е1^,

где i - мнимая единица, ^ - сдвиг фазы колебаний в стоящих рядом частях группы трансляций, —я < f < я. В дальнейших рассуждениях задача Т совместно с (4) называется задача Т (f).

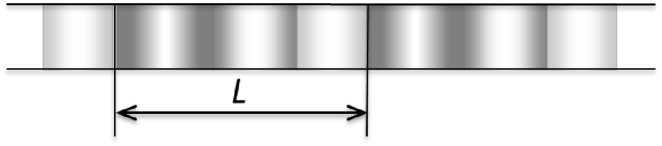
Рис. 2. Фундаментальная ячейка в цепочке неоднородностей.

Исследуя задачу Т (f) в одной фундаментальной ячейке цепочки трансляций, к примеру, на промежутке 0 < % < 1 и продолжая решение с единичного интервала на всю прямую, получится решение.

Для каждого из слоёв М1, М2, М3, по предположению, линейные концентрации равны к1,к2,к3 соответственно. Чаще всего встречающимися и являющимися наиболее общим случаем - свойство монодисперсности цепочки неоднородностей. В текущей задаче монодисперсность выражается в условии к1 = к2 = к3 = 1

Учитывая общий вид решений (2), получаем, что в фундаментальной ячейке граничные условия будут выражены следующими соотношениями:

a1ei!nk1 + b1e ittk! =

_a2e^ ^kiK^2 + _Й2е^-^^к К 12

a2ein(k1+k2)K12 + b2e—in(k1+k2)K12 = a3ein(k1+k2)K13 + b e~in(k1+k2)K13 T21(a1eink1 — b1e-ink1) = K12(a2eink1K12 + b2e-inkK12)

T32K12(a2ein(k1+k2)K12 + b2e-in(k1+k2)K12)

= K13(a3ein(k1+k2)K13 + b3e-in(k1+k2)K13)

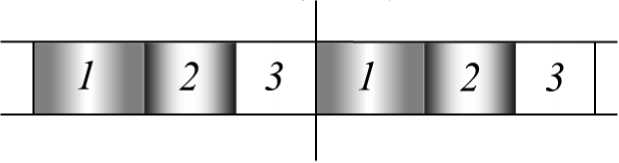
Рис. 3. Граница двух фундаментальных ячеек

Изменения вида кинематических и динамических условий на границе двух фундаментальных ячеек происходят из-за учета условий сдвига фазы колебаний.

a3einK13 + b3e inK13 = a1ei^ + b1e i^ T13^13(a3einK13 — b3e-inK13) = a1ei^ — b1e-i^

В общем виде можно переписать свойств для соседних двух ячеек так:

p(3)(1) = p(1)(0)e^, 43?£3)(1) = p£1)(0)eR

Дисперсионное соотношение. Объединяя в систему уравнения задачи Т (f) и уравнения (4) для сред М 1 , М₂ , М₃ получаем задачу ТМ (f), которую можно записать в виде эквивалентной ей СЛУ Л(Ю)У = 0, где У = (a₁,b₁,a₂,b₂,a₃,b₃) - вектор неизвестных констант в (2). Матрица Л(П) этой системы имеет вид:

/	e ink1	e -ink 1	_einK 12 k 1	_einK 21 k 1	0	0	\
г	о ink- , 21e	—r 21 e-ink1	—K12einK12k1	K2ie-inK12k1	0	0
	0	0	e i4K 1 2(k 1 +k2)	e -i4K 1 2(k 1 +k2)	_e i4K 13 (k 1 +k2)	_e -i4K 13 (k 1 +k2)
	0	0	T32Ki2einK 1 2(k 1 + k2)	_r32K12e-inK 1 2(k 1 + k2)	_K13e i4K 13 (k 1 +k2)	K13e-inK 13 (k 1 + k2)
	-e^	-e^	0	0	einK 13	e -inK 13
\	_e^	ei ?	0	0	T 13 K 13 einK13	_T 13 K 13 einK13	/

Как известно, существует нетривиальное решение системы линейных алгебраических уравнений (СЛАУ), когда определитель матрицы A(Ω) обращается в нуль. Из этого следует, что значения волнового числа, связанные с задачей TM, становятся нулями аналитической функции detA(Ω). Следовательно, волновые значения П*(^) в задаче TM на вещественной оси дискретны и непрерывно зависят от параметра ξ в пределах множества |f| < тт, а также от Ч, и Ktj.

При фиксированных значениях параметров T_t j , K_t j и k_t , уравнение detA(Q) = 0 представляет собой дисперсионное соотношение для всех волноводных мод, обозначаемых как Qⁿ = Qⁿ(f), п = 1,2, .... Эти моды представляют собой связные компоненты множества всех волноводных значений задачи ТМ на плоскости (f, П).

2K₁₂K₁₃(cos(f) — cos (k 1 n)cos (k₂nK₁₂cos (k₃nK₁₃)) + ⁽ К 22 Т 32 + K 23 T 23 ) cos ⁽ k i ^) зт^Пк^) sin^n^) + ⁽ K 23^T13 + Ч1Х12 sin(k i ^) cos(k 2 nK 12 ) sin ⁽ k 3 ^K i3 ) + (k ² ₂t₁₂ + t₂₁)k₁₃ sin(k 1 Q) sin(k₂^K₁₂) cos(k₃nK₁₃) = 0

Здесь использовалось равенство k₃ = 1 — k 1 — k₂ для лучшего понимания выражения. Видно, что k 1 и k₂ достаточно, чтобы описать зависимость волноводной частоты от концентраций сред.

Приближение длинных волн. Исключительным интересом обладает исследование распространения низкочастотных (длинноволновых) волн вдоль одномернопериодической последовательности неоднородностей. В данном контексте наблюдается явление, при котором период структуры и размеры неоднородностей значительно меньше длины волны. Как было указано ранее, волноводные значения задачи TM представляют собой корни уравнения detA(Q) = 0. При П ^ 0 волноводное значение соответствует П1, являющемуся волноводному значению задачи ТМ, ассоциированному с самой низкой частотой волновых колебаний в монодис-персной последовательности сред. Далее мы представим определение для такой моды колебаний.

Опр. Мода колебаний, которая соответствует самой низкой волноводной частоте, будет называться ползущей.

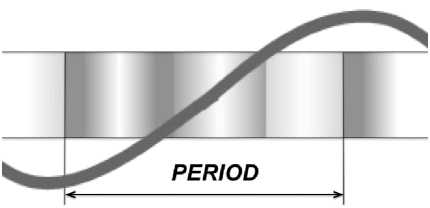
Рис. 4. Длинная (низкочастотная) волна.

Допуская разложение определителя матрицы, или дисперсионного соотношения, в задаче приближения ползущей моды, в ряд Тейлора в точке при П = 0, и принебрегая слагаемыми порядка три (П3) и выше, получаем разложение для низкочастотных волн:

2[cosf — 1] + [k1(k1 + k2T21 + k3T31) + k2K22(k1T12 + k2 + k3T32) + k3K23(k1T13 + k2T23 + k3)]n2 = 0, которое позволяет позволяет найти приближенное выражение для низких волновых частот ползущей моды несложным образом:

лчя

= J                              2(1-cosf)

J k i⁽ k i + k 2 i 2i + к з Т з1) + k 2 K 22⁽ k i T i2 + k 2 + к з Т з ₂ ⁾ + к з К 2з⁽ к 1 Т 1з + k 2 T 23 + к з )

Далее, для вычислений потребовались численные значений плотностей и скоростей звука сред структуры «кварц-вода-воздух».

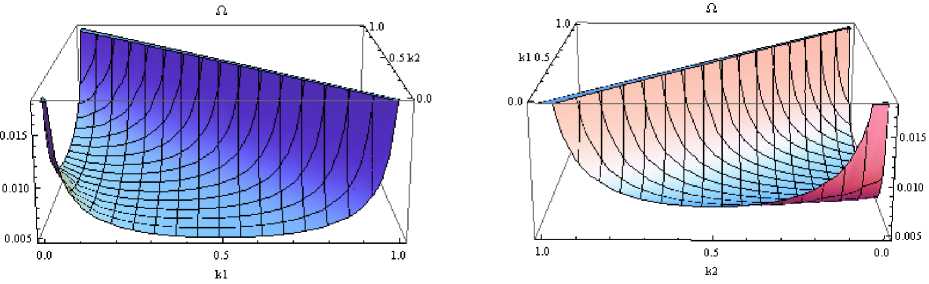
Рис. 5. Зависимость волноводной частоты ползущей моды от концентраций к₁ и к₂ с учетом заданного параметра ^ = и и равенства к₃ = 1 — к₁ — к₂.

Таблица 1. Скорость звука и плотноть среды

Название среды	Скорость звука в среде, м/с	Плотность среды, г/см3
1. Кварц	6000	2.6
2. Вода	1500	1.0
3. Воздух	330	1.2 10-3

Так же можно более наглядно представить полученные результаты – рассмотреть ширину полос пропускания в разрезе, как функцию одной переменной.

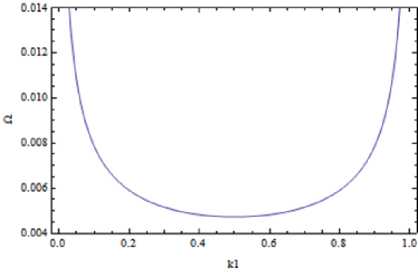
Рис. 6. Ширина полосы пропускания, «кврац-воздух» к₂ = 0 (слева), «вода-воздух» к₁ = 0 (справа).

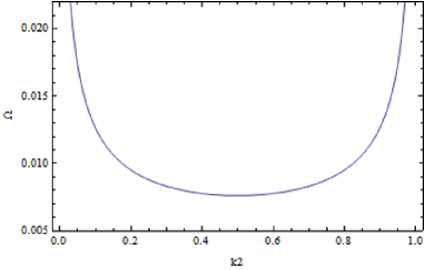
Важно отметить, что волноводная частота ползущей моды, приближенно равная нулю (Ω≈0), существенно зависит от линейных концентраций. На Рисунке 6 видно, что в обоих случаях существует локальный минимум в точках к₁ = 0,5 для

«кварц-воздух» и к₂ = 0,5 для «вода-воздух» , при этом полоса пропускания ползущей моды расширяется к крайним точкам 0 и 1.

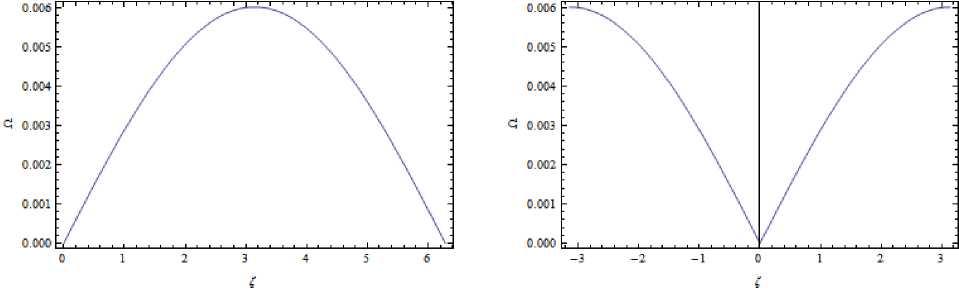
Рис. 7. Зависимость волноводной частоты для первой волноводной моды от волнового вектора f (слева) и то же самое в промежутке —л < f < л (справа)

По характеру зависимости волноводной частоты от параметра сдвига фазы видно, что среда является сильно диспергирующей.

Заключение

На основании проведенного исследования можно выделить следующие ключевые выводы. В общем случае, было изучено распространение акустических волн в неоднородных одномерно-периодических структурах, и было выведено дисперсион- ное соотношение для всех волноводных моделей.

Было получено явное выражение для низких волноводных частот в пределе длинных волн. Также были определены полосы пропускания и полосы запирания для выбранной цепочки неоднородностей, включая «кварц-вода-воздух».

Результаты данной работы имеют по- тенциал для применения в последующих исследованиях в области распространения волн в слоистых фононных кристаллах.