Распространение возмущений в пограничном слое в условиях слабого гиперзвукового взаимодействия

В условиях слабого гиперзвукового взаимодействия могут проявляться эффекты распространения возмущений вверх по потоку. Эти эффекты влияют на. характеристики обтекания тел, в частности на. силы и моменты. Ранее такого рода, режимы не рассматривались.

Рассматривается пластины потоком под нулевым углом атаки, в предположении о том, что число Маха, набегающего потока, велико и что реализуется режим слабого гиперзвукового взаимодействия.

М ^ т ^ 1, г де т - безразмерная толщина пограничного слоя.

Для декартовых координат, отсчитываемых в направлении набегающего потока, и по нормали к поверхности, времени, компонентов вектора, скорости, плотности, давления, полной энтальпии, динамического коэффициента, вязкости приняты следующие обозначения: l_x, 1 у, l t /и^, и ^ и, и ^ и, и _х w, p o p, р ^^^ р, н ^ д, ДоД Параметр l - некоторая характерная длина, (например длина, образующей поверхности в продольном направлении); т = (pu^l/до)^-1/², где индексом << то >>, отличены размерные величины в набегающем

потоке; цо - величина динамического коэффициента вязкости, определенного при температуре торможения. Предполагается, что газ является термодинамически совершенным и характеризуется постоянной величиной отношения удельных теплоемкостей у. Хотя в гиперзвуковых потоках эффекты реального газа существенны, в данной работе они не рассматриваются, поскольку их учет в принципе не меняет соотношений, полученных ниже. Число Рейнольдса велико, но не превышает критической величины, при которой происходит .ламинарно-турбулентный переход. Известно, что для сверхзвуковых и гиперзвуковых течений число Рейнольдса перехода достаточно велико. Предполагается также, что динамическая вязкость линейно зависит от температуры, так что рц = const. Система уравнений пограничного слоя имеет вид дри дри дх ду

ди

ди

Р^иЛ" ⁺ Р^иЛ" дх ду pu^L + ри^ + 2 6 [N ₍₁ — 1₎и|^и] дх ду ду Pr дх

д ди дуЦ ду д ц ди ду Pr ду

с граничными условиями:

и ^ 1; g ^ 1, при у ^ то, и = v = 0; g = Tw/ТЕ, при у = 0, и = 1; v = 0; g = 1, при х = 0.

Для интегрирования указанной системы перейдем к переменным Дородницына-Лиза.

^(х,у) ^ е(х) =

<^х,у") =

(е,^)[2]

Ж

/ р w ц w u _ю dх

ДУ-/о ^

д f и = дһр система уравнении в новых переменных принимает вид

(Nf‘‘)‘ + f f‘‘ (Ng)' + fg' + 2[N(1 - -1)f'f‘‘]‘ Pr                 Pr

N

2e(f 'f‘ -ff‘‘), ■

2e(f'g -fg'), рц    , д      д

’^ = Л"’^ = л-, Р w Ц w ду    де

с граничными условиями

е = 0; f у = 0;f Tw gw = -^’У

^Т 0

ц

= y,g = 1

= ^f' = ⁰’ g = g w

^ ^то; ^f' = 1,g = 1

= сТ ^ш ,N = ( f - 1 ^T w

3. Распространение возмущений в пограничных слоях при слабом взаимодействии

Ранее анализ процессов распространения возмущений проводился для сверхзвуковых течений в условиях сильного взаимодействия или для течений в каналах. Хотя оригинальная работа, была, выполнена, для течений в каналах (интеграл Пирсона), оставался вопрос

о применимости интеграла для других течений или для других режимов взаимодействия, например, для режима слабого гиперзвукового взаимодействия. Мы оставляем предположение о большой сверхзвуковой скорости внешнего потока, что необходимо для получения фиксированной толщины пограничного слоя из-за разрывного распределения плотности вблизи внешней границы пограничного слоя. Мы ограничимся здесь рассмотрением двумерного случая, полагая, что распространение на трехмерный случай можно осуществить так же, как и в выполненных ранее для режима сильного взаимодействия работах.

В условиях быстрого перехода в пограничном слое можно пренебречь рядом членов. Тогда система уравнений, необходимая для описания перехода, имеет вид

/4' -ff‘‘ =    (7 1)   (g -f‘2),(1)

2^р de f‘д - fg  =  о,(2)

о  =  - / (g - j‘2)dg.(3)

P. /0

Вид константы в выражении для толщины вытеснения не имеет значения, поскольку дальнейший анализ связан с нахождением производной толщины вытеснения по давлению и с приравниванием этой производной нулю. Это соответствует нахождению состояния, в котором среднее по профилю число Маха равно единице.

do dp

-

-

∞

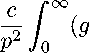
(|g - ^ ^=о. op op

Найдем производные, входящие в вышенаписанную формулу. Для этого уравнение (1) можно переписать в виде

f ‘2 9 (f ) = - (~    H dP Эр f ‘       27P de	(g - f ‘2).	(5)
Тогда
f = -(f ‘+«)Д-7 27P de	f 4 (g -f ‘2) , J о (f‘ + «)2d’-	(6)
Переходя к дифференцированию по давлению можно получить
»4 = - ( ‘ + a)!7-1 UP                27P ,	f 4 (g -f ‘2) , 1 о (f‘ + a)2 dn'	(7)
Используя уравнение (2) можно получить
dg = -g (7 -1) Г dP             27P ,/о	(g - f ‘2) , (f ‘ + a)2 dd‘	(8)

Преобразуем выражение (7)

(dj‘)  ₌   __f„ (7 -1) f (д - f ‘²) , __(f,. .7—1 (g - f ‘²)

dp ^J 27P ,/o (f‘ + a? ^{4 (J + a)} 27P (f‘ + a)²'

Теперь можно вычислить интегралы, входящие в выражение (4):

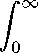
Sg

6Pd^

Д-1 g Г ²7P    ./о

д - f ‘² (f ‘ + a)²

d^ +

(7 - 1) 27P

∞

g(g - f ‘²) (f ‘ + a)²

d^

[ “ f ^f'

^f ЛГ^ = J о     dp

-

(7 - 1) Г 27Р Jo

∞

(g - f'²L (f' + а) ^dr

-

(7 - 1)

27Р

∞

/ (g - f" ² W

(И)

После ряда преобразований выражения (11) получаем f “ , ,df'

о

-

(7 - 1)(f' + а)² Г

27Р

(g - f'²L (f + а)^{2 dr}

-

(7 - 1) 27Р

∞

/  (g - f^dr.

Объединяя выражения (10) и (11) можно получить

-

2f T dr op

(7 - 1) Г 27Р Jo

g(g - f ²) (f + а)²

dr + (7-^ P(g - f'2)dr

7Р 0o

Подставляя (13) в (4), окончательно получим dcr dp

_c (7 - 1) Г 27Р 0o

(g - П2

(f' + а)2 dr

-

c 1 г

7 ./о

Для одномерной газовой динамики обращение в ноль такой производной означает достижение равенства скорости звука и скорости потока. В нашем случае мы имеем дело с двумерными течениями газа. В то же время полученные соотношения относятся к осред-ненным по поперечной координате величинам. Поэтому полученное соотношение можно трактовать как достижение равенства средней скорости звука средней скорости потока. Средняя скорость звука и есть в данном случае скорость распространения возмущений вверх по потоку. Таким образом, соотношение, определяющее скорость распространения возмущений, имеет вид

∞

(g - f²)² (f + а)²

d} - / (g - f^d} 0

В работах [3, 4] рассматривается распространение возмущений в пограничных слоях в сильной теории взаимодействия и получается выражение для нахождения а — скорости распространения возмущений. Можно показать, что и в случае слабого вязко-невязкого взаимодействия справедливо соотношение, определяющее скорость распространения возмущений в пространственных течениях.

(7 -1) p (g - n² - w²)²

2    Jo (псовӨ + гизгпӨ - а)²

∞

-

n2 - w2)dr

0,

где u, w , - профили продольной и поперечной скорости, - профиль полной энтальпии, Ө - направление распространения возмущений.

4.    Результаты расчетов

Система уравнений

(Nf )^w + f f‘‘

(7/)' + fg’ + 2[N(1 - b)f'f '']'

0,

проинтегрирована численно, и для полученных профилей компонентов скорости и энтальпии n, g, используя приведенный выше интеграл, можно найти и величины скорости распространения возмущений в пограничном слое.

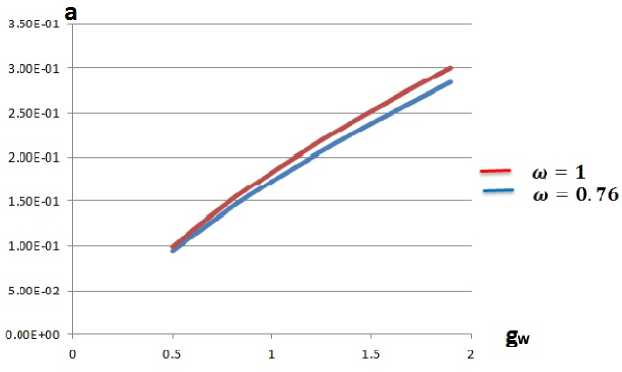
Рис. 1. Зависимость скорости распространения возмущений вверх по потоку от температурного

фактора при ш = 0.76 и ш = 1

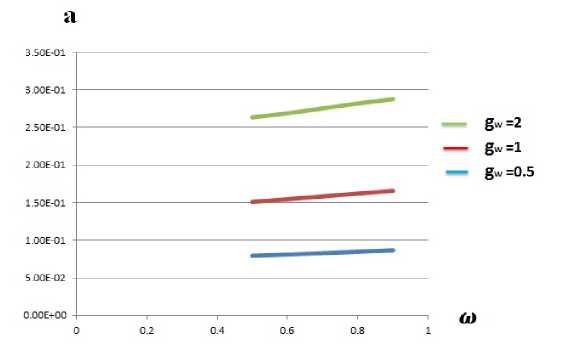
Рис. 2. Зависимость скорости распространения возмущений вверх по потоку от показателя степени для разных величины температурного фактора.

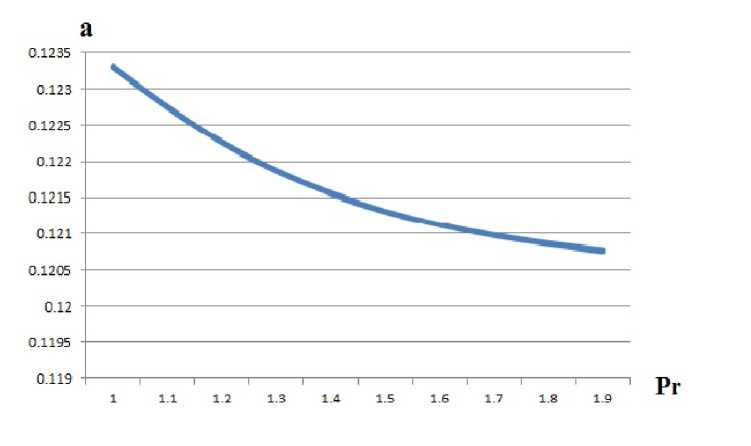
Рис. 3. Зависимость скорости распространения возмущений вверх по потоку от числа. Прандтля

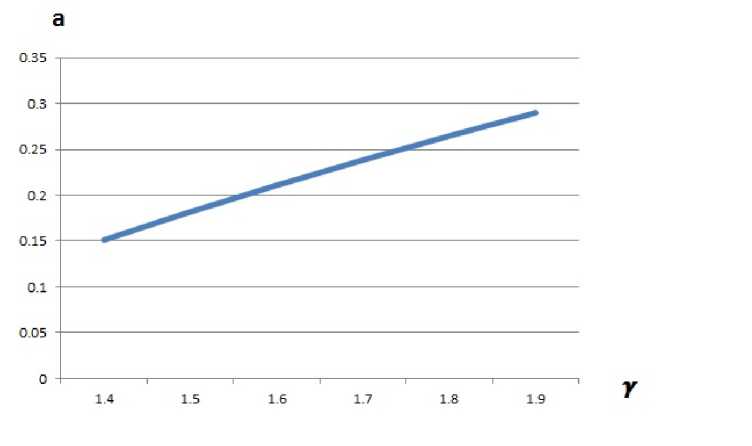
Рис. 4. Зависимость скорости распространения возмущений вверх по потоку от показателя теплоёмкости

Результаты получены для величины угла распространения Ө = т, т.е. вверх по потоку. Были получены данные для ряда значений температурного фактора gw при ш = 0.76 и ш = 1. Получена зависимость скорости распространения возмущения от показателя ш для разных значений температурного фактора gw (gw = 0.5; gw = 1; gw = 2).

На рис. 1 и рис. 2 приведены зависимости скорости распространения возмущений вверх по потоку от величины температурного фактора и показателя. Можно отметить, что с ростом температурного фактора и показателя степени величина скорости распространения возмущений растет. Этот эффект объясняется ростом температуры в пристеночной области и относительным увеличением области дозвукового течения в пограничном слое. Отметим, что при относительном уменьшении области дозвукового течения скорость распространения возмущений стремится к нулю, если стремится к нулю температурный фактор.

Влияние числа Прандтля на скорость распространения возмущений представлено на рис. 3. Показано, что с увеличением числа Прандтля скорость распространения возмущений уменьшается. Также исследовано влияние показателя адиабаты у на скорость распространения возмущений в пограничных слоях при слабом взаимодействии. Отметим, что величина скорости распространения возмущений расчет с ростом отношения удельных теплоёмкостей у.

5.    Заключение

Исследованы эффекты распространения возмущений в пограничных слоях в условиях слабого вязко-невязкого взаимодействия. Показано, что полученные ранее соотношения для определения скорости распространения возмущений для режима сильного гиперзвукового взаимодействия справедливы и для описания режима слабого гиперзвукового взаимодействия. Определены зависимости скорости распространения возмущений при различных величинах параметров характеритик пограничного слоя. Полученные данные могут быть использованы при определении характеристик аэродинамических органов управления, вы-сокоскростных летательных аппратов.