Распространение возмущений в сверхзвуковых пограничных слоях

Распространение возмущений в пограничных слоях связано с процессами конвекции и диффузии [1]. Анализ системы уравнений трёхмерного пограничного слоя [1] показал, что характеристиками этой системы уравнений являются линии, нормальные к обтекаемой поверхности. Вид этих характеристик и условия, выполняющиеся на них, соответствуют распространению возмущений с бесконечной скоростью по нормали к поверхности. Эти эффекты связаны с процессами диффузии, которые в вырожденной, по отношению к исходным уравнениям Навье–Стокса, системе уравнений пограничного слоя проявляются в одном направлении и определяются старшими производными в краевой задаче. Для описания процессов распространения возмущений, связанных с конвекцией, необходимо анализировать характеристики системы уравнений пограничного слоя без старших производных (субхарактеристики). Полная система характеристик и субхарактеристик позволяет на качественном уровне сформулировать условия корректности краевой задачи и определить зоны зависимости и влияния. Уравнения двумерного нестационарного пограничного слоя также допускают анализ системы характеристик и субхарактеристик [2]. Исследование характеристик и субхарактеристик в нестационарных пограничных слоях, содержащих возвратные токи, привело к выводу о возможности, с течением времени, возникновения разрывных решений [3].

Вместе с тем из-за условий прилипания на поверхности и наличия области дозвукового течения существует возможность распространения возмущений, обусловленная волновыми процессами. Результаты экспериментальных исследований эффектов распространения возмущений вверх по потоку в сверхзвуковых пограничных слоях изложены, например, в [4]. Математическая модель, описывающая распространение возмущений, предполагает, что распределение давления определяет- ся в результате взаимодействия течения в пограничном слое с внешним потоком. В то же время классическая теория пограничного слоя не позволяет описывать подобные процессы, так как предполагается, что распределение давления заранее известно. Эффекты сильного локального вязконевязкого взаимодействия существенны не только при распространении возмущений вверх по потоку. Учёт этих эффектов позволил описать локальные отрывные течения [5--6], а также течения в областях с большими локальными градиентами [7-- 9].

Анализ процессов распространения возмущений в трёхмерных пограничных слоях для режима сильного взаимодействия позволил определить соответствующие субхарактеристические поверхности [10], отделяющие области докритического (дозвукового в среднем) течения и закритическо-го (сверхзвукового в среднем) течения в гиперзвуковом пограничном слое вблизи треугольного крыла. Определение до- и закритических течений сформулировано [11] для течений, в которых возмущения распространяются вверх по потоку на расстояния, значительно превосходящие толщину пограничного слоя или на расстояния, сравнимые с толщиной пограничного слоя, соответственно.

Ниже исследованы нестационарные течения в ламинарном пограничном слое для условий сильного взаимодействия. Источником нестационарных возмущений, приводящим к проявлению процессов вязко-невязкого взаимодействия, может быть меняющееся во времени донное давление, падение на пограничный слой ударной волны переменной интенсивности и др. Как показано при исследовании гиперзвуковых течений [12], для стационарного режима сильного взаимодействия характерным является распространение возмущений вверх по потоку вдоль всей поверхности вплоть до передней кромки. Естественно предположить, что аналогичные эффекты будут проявляться и в нестационарных течениях, изменяя как локальные, так и интегральные величины поверхностного трения, теплового потока и давления.

Моделирование такого рода процессов имеет поэтому значение для решения задач практической аэродинамики.

II.    Постановка задачи

Рассматривается обтекание плоской поверхности (пластины или клина), расположенной под нулевым углом атаки к набегающему гиперзвуковому потоку вязкого теплопроводного газа. Предполагается, что реализуется режим сильного взаимодействия [13], для которого характерны следующие соотношения:

M то ^ го,    M то Т ^ го,         (1)

где M _∞ — число Маха набегающего потока, τ — безразмерная толщина ламинарного пограничного слоя ( т = O (Re o ¹ / 2 )). Для декартовых координат, отсчитываемых вдоль поверхности пластины и по нормали к поверхности, времени, компонентов вектора скорости, плотности, давления, полной энтальпии, динамического коэффициента вязкости, введены следующие обозначения: lx , ly , lz , lt/и то , U to U , U to V , U to W , Р то Р , P to U 2 _TOP , u TO H/ 2, μ 0 μ соответственно. Параметр l представляет собой характерную длину пластины или расстояние от передней кромки до донного среза клина. Индекс бесконечность относится к размерным параметрам невязкого потока над пограничным слоем, нулевым индексом отмечена размерная величина динамического коэффициента вязкости, вычисленного при температуре торможения. Препо-лагается, что число Рейнольдса Re ₀ = р_тои_то1/р 0 велико, но не превосходит критического значения, при котором возможен переход ламинарного режима течения в турбулентный. Известно, что с ростом числа Маха число Рейнольдса перехода значительно возрастает [14].

В соответствии с теорией сильного гиперзвукового взаимодействия область возмущённого течения вблизи обтекаемой поверхности разделяется на две подобласти: 1 — невязкое течение, 2 — пограничный слой.

Области 1 соответствуют следующие асимптотические представления функций течения и координат:

x = x 1 ,     y = ту 1 ,     t = 1 1 ,        (2)

u ( x,y,t,T ) = 1 + ...,v ( x,y,t,T ) = v 1 ( x 1 ,y 1 ,t 1 ) + ...,

P ( x,y,t,T ) = т ² p 1 ( x 1 ,y 1 ,t 1 ) + ...,

Р ^{( x,}y^,t,T ) = р 1 ⁽ x 1 ,y 1 ,t 1 ) ⁺ ...

Подстановка разложений (2) в систему уравнений Навье–Стокса и предельный переход (1) приводят к системе уравнений вида др 1 + др 1 + др 1 v 1 = 0

∂t1 ∂x1     ∂y1      , dv 1 + dv 1 + dv 1 + 1 dp 1 =0

∂t 1     ∂x 1     ¹ ∂y 1     ρ 1 ∂y 1      ^,

A ( p - ) + v , JL ( p - ) = o

∂x 1 ρ ₁        ∂y 1 ρ ₁

со следующими граничными условиями на ударной волне:

y 1 = g 1 ^{( x} 1 ,t 1 ) ,

Р 1 =

⁽ Y ⁺ 1)

( Y - 1) ’

( Y + 1) v 12 ^{p 1} = —2— ,

v 1 =

• 2 ₍ dg 1 + dg 1 .

( y + 1) dx 1

и на внешней границе пограничного слоя 2     d^ 1

y, = 5 1( x 1,(,) ,v 1 = ^C gx; +)

Для дальнейшего анализа необходимо получить связь между толщиной пограничного слоя δ 1 или вертикальной скоростью v 1 ( x 1 ,5 1 ,t 1 ) и возмущением давления p 1 ( x 1 ,t 1 ). Ниже использовано приближённое соотношение

P1 = (Y + 1) v 2 / 2, которое представляет собой обобщение формулы касательного клина на нестационарный случай.

Для области 2 характерны следующие асимптотические разложения и представления координат:

x = x 1 ,     y = Ty 1 ,     t = 1 1 ,        (3)

u ( x,y,t,T ) = u 2 ( x 1 ,y 1 ,t 1 ) + ...,v ( x,y,t,T ) =

= TV 2 ( x 1 ,y 1 ,t 1 ) + ...,

P ^{( x,}y^,t,T ) = ^{T 2} P 2 ^{( x} 1 ,t 1 ) ⁺ ...,Р ^{( x,}y^,t,T ) =

= T ² Р 2 ( x 1 ,y 1 ,t 1 ) + ...,

H ( x,y,t,T ) = H 2 ( x 1 ,y 1 ,t 1 ) + ...

Подстановка разложений (3) в систему уравнений Навье–Стокса и предельный переход (1) дают систему уравнений нестационарного пограничного слоя. Замена переменных

X = x 1 , T = 1 1 ,

_ 2 yC 0 !- 1 / 2 - 1 / 4 " f          _ dF

^Y = [( _Y - 1)]     ^x 1       ^{Rdy 1 ,u 2} = dY,

P 2 = x ^{- 1} / ² P , р 2 = x ^{- 1} / ² R , C 0 = P x =0 , G = H 2 , A = G — U ² приводит соответствующую краевую задачу к виду

X dU XUI^9U dF dU d Ф dU F dU

X dT ⁺ ( U dX - dXdY - dZ dY ) - 4 dY ⁺

^{+ в (Л}4^Г A =⁽ C o ) dY 2 ,       ⁽⁴⁾

_v dG  _VG_T9G dF dG d Ф dG   F dG

^X dT ⁺ ( U dX - dX dY - dZ dY ) - 4 dY =

₌ v ( Y — 1) _A dP₍CC 2 G

YC dT ⁺⁽ C 0 ) dY ² ,

∞

в = - 1 + ^XdX,  Д-^]2j A2dY,

(y +1),ЗД     dA  9A 2

P 2      + X(dX + T)] ’

U = F = Ф = 0,   G = g„,   Y = 0;

U = G =1, W = 0, Y = те,

P [ X,Z = в (X) ,T ] = у (X,T), где предполагается, что динамический коэффициент вязкости линейно зависит от температуры, а последнее краевое условие соответствует заданной зависимости донного перепада давлений от времени.

III.    Анализ субхарактеристик

Определим вначале характеристические (субхарактеристические) поверхности fi( X,T ), связанные с функцией P ( X,T ), которая не известна заранее и определяется в процессе решения.

После замены переменных

X,Y,T ^ fi,Y,T краевая задача

(4) принимает вид

∂U b ⁽ San

∂F ∂U ∂P

dfi dY + Adfi) B

Для вычисления производных по переменной fi, входящих в подынтегральные выражения, можно использовать задачу (4), откуда следует, что

Y         Y

∂F S ∂P A        B

dfi = - P dfi + J S2 dY + S J S2 dY,

dG _ 1 dF dG D 2CAaT dP

Ifi = Sdfi dY + S + S dfi.

После ряда преобразований, используя соотношения (5)-- (6), можно получить выражение

∂P

bNdfi = PM, где

M =

∞∞∞

| BdY - S ² | SB ; dY - | SdY - ( 2^- 1 C о ) c,

∞∞ A2

N = ] S2 dY - (7-1) J AdY

Условие, определяющее субхарактеристическую поверхность, имеет вид

∞∞

(2:-r1 J (G-UFdY -1 (G - U2)dY = 0, (7)

Здесь

∂G b(San

∂F ∂G      ∂P

dfi dY 2 CAadfi) = D. (5)

где параметр a определяет среднюю скорость звука или скорость перемещения субхарактеристической поверхности.

С тт          9 fi/9 Qa

S = U + a,a = dT(dX)

1 b =X^ , b XdX,

a = (dfi/dX)(dfi/dT)“1 = -dX/dT.

∂2U  F ∂U

= [ dY2 + 4 dY +

(Y - 1) A

4 y

∂U

X dTJ’

C=

∂2G  F ∂G

= [ dY2 + 4 dY

(Y - 1)

2yP , dp

+ 2 XCAdT

∂G

XdT].

Условие взаимодействия, связывающее распределение давления и толщины вытеснения пограничного слоя, может быть преобразовано следующим образом:

b(1 + a>

= с,

с = (2P)1 /2(y - 1)“1 /2

зД - XdA.  (6)

Производная в левой части

равенства (6) может

быть выражена в соответствии с приведённым выше выражением для толщины вытеснения:

d A _ dfi = [

(Y - 1) C 0 ]1 / 2 x

2 yP 2

∞

x [ I* (Ц - 2UdU)dY -d fi       d fi

1 dP Pdfi

∞

| AdY].

Выражение (7) представляет собой обобщение интеграла Пирсона [15]:

L = J (G -2U2) dY - J (G - U2)dY, (8) 00

знак которого зависит от средней величины числа Маха в пограничном слое. В среднем сверхзвуковому течению соответствует отрицательное значение интеграла, в среднем дозвуковому течению соответствует положительное значение интеграла.

Соотношение (7) имеет простой физический смысл. В гиперзвуковом пограничном слое существует средняя по профилю скорость потока. Тогда если средняя скорость звука меньше средней скорости потока, то течение в пограничном слое докритическое и возмущения распространяются вверх по потоку. Соответственно течение будет закритическим в случае, когда средняя скорость больше скорости звука.

Формула (7) может быть получена из (8) более простым способом. Перейдём от неподвижной системы координат X,T к подвижной X 1 ,T , перемещающейся вверх по потоку с постоянной скоростью:

X 1 = X + aT.

В подвижной системе координат скорость в пограничном слое становится равной U 1 = U + a , а разность G 1 — U 2 = G — U ² не меняется, поскольку пропорциональна температуре газа. Подставляя выражения для функций U 1 и G 1 в формулу (8), получаем формулу (7) с точностью до замены U 1 ,G 1 на U,G .

Значению a >  0( a <  0) соответствует звуковая волна, распространяющаяся вверх (вниз) по потоку. При этом первый интеграл в (7) сходится при a <  0, так как |a >  1 1 .

Следует отметить, что полученное выше выражение (7) выведено на основании анализа распространения малых возмущений, описывающихся задачей (4), в предположении, что профили скорости и энтальпии не меняются в первом приближении при распространении волны возмущения. В этом случае в качестве таких профилей использованы решения стационарной задачи для пограничного слоя в условиях сильного взаимодействия.

IV.    Примеры решений

В качестве примера приведём зависимости скоростей распространения волн вверх по потоку от отношения удельных теплоёмкостей и от числа Прандтля, полученные для случая решения автомодельной системы уравнений.

Для нахождения автомодельных решений использована преобразованная система уравнений (4), в которой профили скорости и полной энтальпии не менялись. Поскольку изменение продольной координаты линейным образом входит в формулу для определения скорости распространения возмущений, то вид этой формулы также не меняется.

Профили скорости и полной энтальпии получены в результате решения следующей краевой задачи:

U" + FU' + (Y—1) (G — U2) = 0, γ

—G" + FG' + 2(1 — —)(U 'U")' = 0,   (9)

Pr                Pr

п = 0, U = F = 0, G = Gw,

П ^ го, U = 1, G = 1.

Представленная система уравнений выведена для случая линейной зависимости динамического коэффициента вязкости от температуры.

Полученные в результате численного решения задачи (9) профили скорости и полной энтальпии использованы для определения скорости распространения возмущений вверх по потоку.

На рис. 1 представлены зависимости скорости распространения возмущений вверх по потоку a от отношения удельных теплоёмкостей γ . Приведены три кривые, соответствующие различным значениям числа Прандтля. Нижняя кривая соответствует числу Прандтля Pr = 0,01, средняя кривая единичному числу Прандтля Pr = 1,0 и, наконец, верхняя кривая соответствует числу Прандтля Pr = 100,0. Можно отметить слабую зависимость процессов распространения возмущений от числа Прандтля. Собственно влияние этого числа сказывается на средних характеристиках профилей скорости и энтальпии.

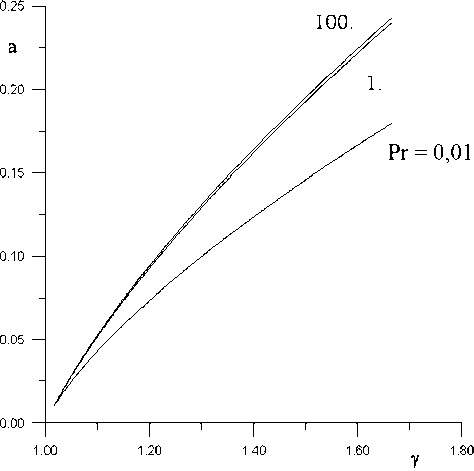
Рис. 1

Предполагалось, что отношение удельных теплоёмкостей меняется от единицы (предельный случай многоатомного газа) до 5 / 3 (одноатомный газ). Можно видеть, что скорость распространения возмущений вверх по потоку a растёт с увеличением отношения удельных теплоёмкостей γ .

Исследуем особенности поведения решения при стремлении отношения удельных теплоёмкостей к единице. Численное решение показывает, что скорость распространения возмущений вверх по потоку также стремится к нулю.

Проанализируем поведение интегралов

ОО                   ОО

(Y—1I(GU—U22 dn—f(G—u 2)*-=0, 00

входящих в формулу для определения скорости распространения возмущений.

При y ^ 1 система уравнений, определяющая профили скорости и энтальпии, приводится для случая линейной зависимости динамического коэффициента вязкости от температуры к уравнению Блазиуса (первое из уравнений системы (9)), решение которого обозначим как u 0 и g 0 . При малых значениях поперечной координаты имеем

uо«bn + O(п2) ,gо ~ gw + о (п).

Первый из интегралов представим в виде

∞

ti-! 7 (go - udn —

2 J (uo + a )2

(7 — 1)rfr(9o — u0)2        gW    i , ,

2 fJ        —       d+

1 ∞

7    gW    d f(9o— u0)2}

+ J (bn + a)2 n + J (u0 + a)2 '

Поскольку скорость распространения возмущений стремится к нулю, можно привести интеграл к виду

(7 — 1)

(go J[   (uo)2

u 2 ) ²

g

w

(bn)2

]dn+

+gw (1 ba

∞

b >+!6! u o)2

u 2 ) ²

}•

Введём далее обозначения

Io —

(7 — 1)

{[[ g.

J [   (uo)2

u 2 ) ²

g _w ²

(bn)2

]dn - gw}■

11 —

(7 — 1)

∞

[ ( g o_________

J      (uo)2    ’

u 2 ) ²

∞

I2 —

|(9o — uo)dn^

о

В результате получим

T , T T _   (7— 1) gW

I°+ I1 — I2 =    2b^

.

Следовательно, при стремлении отношения удельных теплоёмкостей к единице скорость распространения возмущений вверх по потоку пропорциональна 7 — 1:

a—

(7 - 1) gW

2 b (12 — 11 — 10) •

Работа выполнена при частичной поддержке РФФИ (грант № 07-01-00609 а).