Рассеяние когерентного света по поверхности с конечной проводимостью

Дифракционные оптические элементы, используемые в задачах лазерной технологии, например, фокусаторы [1], имеют зонированную рельефную хорошо отражающую поверхность. Причем глубина рельефа меньше половины длины волны, а линейные размеры зон убывают от центра к периферии. В центре размер зон порядка сотен длин волн, а на краях оптического элемента - единицы длин волн. Поэтому дифракция лазерного света на такой рельефной поверхности может быть адекватно описана в рамках теории дифракции Кирхгофа.

Однако при расчете дифракционных оптических элементов, как правило, не учитываются многие особенности дифракции света на рельефной поверхности. Хотя очевидно, что энергетическая эффективность — доля отраженной энергии, идущей на формирование требуемого изображения, должна зависеть от состояния поляризации падающегно излучения и от материала поверхности.

В данной работе рассмотрена задача дифракции когерентного света на рельефной поверхности (одномерный случай) с конечной проводимостью в рамках теории Кирхгофа и в приближении дальней зоны. Разработан алгоритм решения такой задача с использованием алгоритма быстрого преобразования Фурье. Последнее обстоятельство позволяет сократить время, затрачиваемое на проведение компьютерного эксперимента. Получены зависимости отраженной энергии от показателя преломления и коэффициента поглощения материала и от состояния поляризации падающего излучения.

1. Дифракция света на рельефной поверхно сти

Комплексная амплитуда электрического вектора световой волны рассеяной на поверхности с конечной проводимостью и одномерным рельефом может быть описана следующим образом [2,3]:

^('р)

ikE₀ exp{27?₀} 4 л Ro

где a = (l-r_F)sin0,+(l+r_F)sin®₂, 6 = (l+r_F)cos©₂+(l-r_F)cosO,, 5, = ^(sin®,-sin®₂), 5_Z =-£(cos®₂ + cos®,), ®₂-угол отражения, r_P -радиус вектор в точку наблюдения Р, к- волновое число, ^(х),^'(х)- уравнение поверхности и ее производная, Гр -коэффициент отражения Френеля, который в зависимости от вида поляризации определяется следующим образом [4]:

cos0, - Ул2 - sin2 0,      _    _ л2 cos0, - Ул2 - sin2 0, rFTE =         / ,     ,   ’ Г™ ~                  . 2

COS0, +Ул2-5Ш20,           л2cosG,+V” -sin 6]

коэффициенты отражения в случае ТЕ— и ТМ—поляризации, соответственно;

9_t = в, - arctg^\x^ -локальный угол

падения, @i - угол падения, и —показатель отражения материала

поверхности.

В случае

проводящего материала обычно

рассматривается

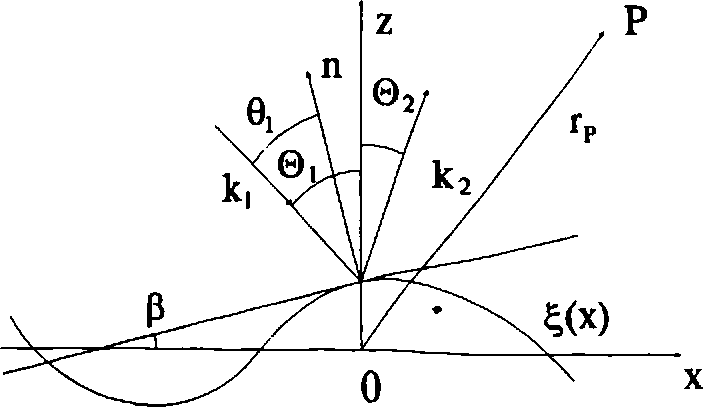
Рис. 1.Рассеяние света на рельефной поверхности.

показатель п = п + ik , где преломления, коэффициент случае проводимости преломления коэффициент

п

комплексный отражения, — показатель к —

поглощения. В бесконечной показатель п-хю, поглощения

к -> 0, следовательно комплексный показатель отражения и -> оо . Подставляя его в формулы (2) получим, что

коэффициенты

отражения

Френеля в этом случае равны:

^rFTE~~ 1 ИЛИ ^rFTM~^ Ео амплитуда падающей плоской волны; /^ =|^|—расстояние от начала координат до точки наблюдения, [—L;L]— участок освещенной поверхности (рис.1.).

Введем р(6₂) = ~" где Е₂ —электрическое поле в некоторой точке зоны

Фраунгофера и Е^ поле, отраженное в зеркальном направлении (0i=0₂) гладкой поверхностью того же размера, с тем же углом падения и на том же расстоянии Ro-Вместо (1) получим выражение для углового распределения комплексной амплитуды рассеянного света

Отсюда

pcea-—1—

4 L cos©

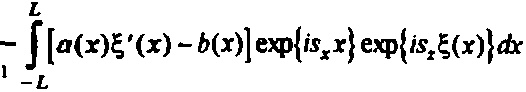
P(0=)=:^^ki(02)+F2(02)sine2 -f3^                   (4)

^(©2)* fw(x)[1*'F("J)]U'(-x)sin®i + “»01)еч,{ч(02)£(_х)}е’ф{_“«(02)х}‘гх          (5)

^(©i) = J Ч^^{1 +} ^-^'(-^ехррхДе, )£(-x)}exp{-z5,(e₂)x} dx

Fik®^ - JM^1 + гг(-х)]ехр{'$г(е2)^(-х)}ехр[4$х(е2)х}dx где nix)= rec/ —

Для того чтобы интегралы в формуле (5), (6) и (7) можно было вычислять с помощью преобразования Фурье, необходимо преобразовать прообраз так, чтобы он не зависел от выходного параметра 02. Наиболее просто это делается для поверхности с периодическим рельефом. Пусть ^(х) периодическая функция с периодом Т, тогда можно записать следующий ряд Фурье

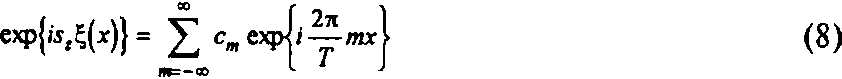
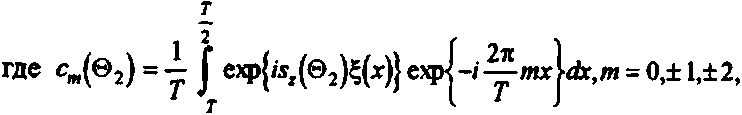
Подставляя формулу (8) в формулу (4), получим выражение для углового распределения амплитуды в виде :

р(02) = 17   Е^^ + А^г^^-А^             (9)

где функции ^,^₂,^з получаются из функций F_X,F₂,F₃ определенных уравнениями (5)-(7), заменой функции exp(/s_z(0₂)£(-x)} на ехр|-йя-^-х}. Для синусоидального рельефа при ^(х) = А₀8й^~^> в уравнение (10) коэффициенты с_т примут вид с_т = J_m(s_z(0₂)*o) ^гД^е Jm(x) ^— функция Бесселя ш—го порядка 1—го рода.

2, Численные результаты.

В случае бесконечной проводимости коэффициенты отражения Френеля равны ±1 и следовательно вид дифракционной картины почти не зависит от типа поляризации. Для

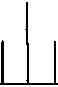
изучения зависимости вида дифракционной картины от вида рельефа были проведены расчеты для поверхности вида:

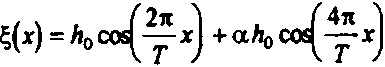
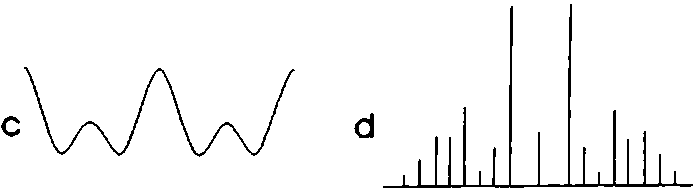
Рис.2. Зависимость дифракционной картины от рельефа поверхности.

при следующих значениях параметра: а=0 (рис.2.а,Ь), а=1 (рис.2.с,д), а=2 (рис.2.е,0- На графиках рис.2.а,с,е показан вид рельефа поверхности, на графиках pHC.2.b,d,f показан вид дифракционной картины по оси абсцисс отложен угол рассеяния - 02, по оси ординат угловое распределение интенсивности рассеянного света - |р(®2)| • Расчет был произведен по формуле (9) и для следующих значений: количество отсчетов

Дискретизации поверхности N=256, период решетки Т—100 мкм, высота рельефа ho 0.325

мкм, длина волны падающего света Х=О.бЗ мкм, участок освещенной поверхности 2L=0.5 мм.Из сравнения графиков видно, что с ростом а происходит расширение диапазона углов рассеяния и перераспределение энергии между дифракционными порядками.

Для выяснения областей изменения параметров в которых алгоритм (формула (9)) дает наилучшие результаты получены зависимости изменения отраженной энергии от высоты

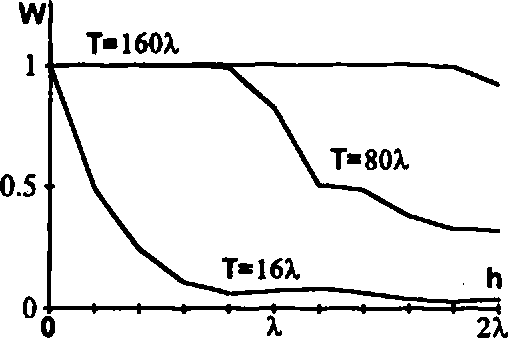
Рис.З. Зависимость энергетической эффективности от высоты рельефа.

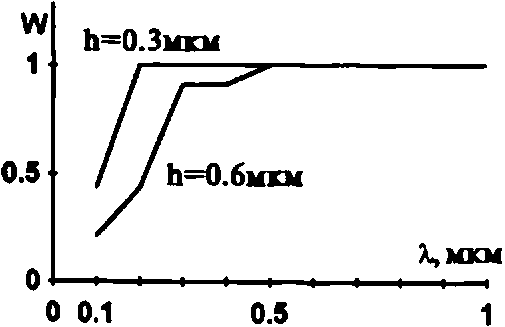
Рис .4. Зависимость энергетической эффективности от длины волны.

рельефа при разных периодах решетки с синусоидальным рельефом поверхности, для нормально падающего света (Рис.З.). Энергия падающего света во всех эксперементах постоянна. Отраженная энергия рассчитывалась как сумма интенсивностей по всем углам из диапазона для которого производился расчет. Из графиков приведенных на рис.З. видно, что чем меньше период тем быстрее убывает величина отраженной энергии с ростом высоты рельефа. Эго можно объяснить следующим образом: при практической реализации алгоритма бесконечная сумма (9) заменяется конечной. А так как с ростом периода решетки и высоты рельефа возрастает вклад отброшенных слагаемых (дифракционных порядков), то рассчитанная энергия уменьшается с ростом высоты рельефа. Из рис.З видно что при числе отсчетов N=256 алгоритм алгоритм дает правильные результаты (W=l) при условии Т>100Х, ho<1.5X. На рис.4. показан график зависимости энергетической эффективности от длины волны падающего нормально света, для решеток из материала с бесконечной проводимостью, с периодом Т=100 мкм и различной высотой рельефа. Количество отсчетов дискретизации поверхности N=256. Как видно из графиков (рис.4.) алгоритм расчета дает правильные результаты (W=l), если длина волны падающего света больше максимальной высоты рельефа поверхности.

Для оценки точности вида дифракционной картины и нахождения минимального числа отсчетов N, которые необходимо выбрать на поверхности для получения хорошего результата был произведен расчет углового распределения амплитуды по формуле (4) методом Симпсона [5]:

М-1

М-1

^02)* ш w=l            m=l

где

, , (£Ит)^£> -к^^Ое^^^г)^,-^)} ехр{-/^(@2)дг/„^

•/W~                 4Zcose,

L

+ mh,x₀ = -L,m = 1,2.. M, h = —

2M — число точек разбиения [—L;L).

Расчеты были произведены для решетки с синусоидальным рельефом со следующими параметрами: период решетки Т=160Х, высота рельефа ho=X/2, угол падения ©!=я/6, 2L=0.5.

Из сравнения результатов, полученных при расчете с помощью алгоритма БПФ по формуле (9) и методом Симпсона по формуле (10) можно сделать вывод, что уже при числе точек разбиения №256 оба метода дают практически одинаковые результаты при выбранных параметрах.

В случае конечной проводимости, коэффициент отражения Френеля, а следовательно и вид дифракционной картины зависят от направления поляризации и вида материала из которого изготовлена отражающая поверхность. Численные эксперементы проведенные для решеток имеющих одинаковые параметры (Т =100 мкм, ho =0.15 мкм), но изготовленные из разных материалов показали, что при изменении материала или состояния поляризации меняется энергетическая эффективность (отношение энергии отраженного света к энергии падающего света). Характер ее изменения показан в следующей таблице:

Материал	Показатель преломления	Коэффициент поглощения	Энергетическая эффективность
			ТЕ-тип	ТМ—тип
серебро Х=0.5893 мкм	0.2	17.2	0.988	0.986
аллюминий Х=0.5893 мкм	1.44	3.6	0.772	0.599
стекло	1.5	0	0.024	0.02
идеальный проводник	ОО	0	0.99978	0.99978

На графиках приведенных на рис. 5. показана зависимость энергетической

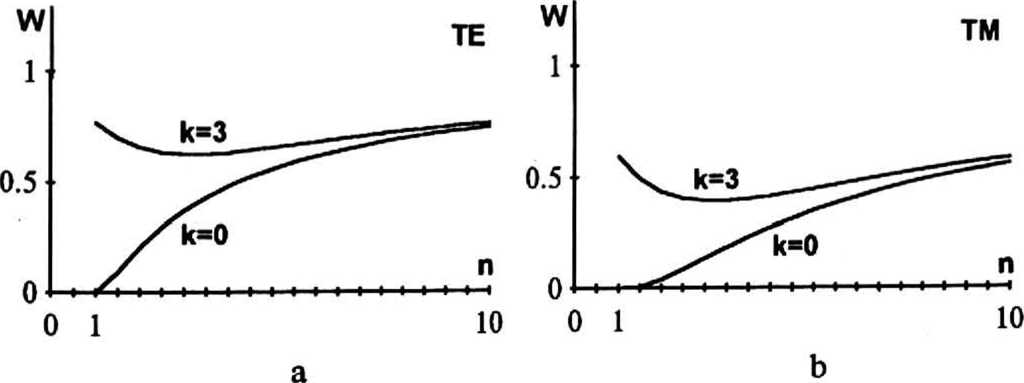
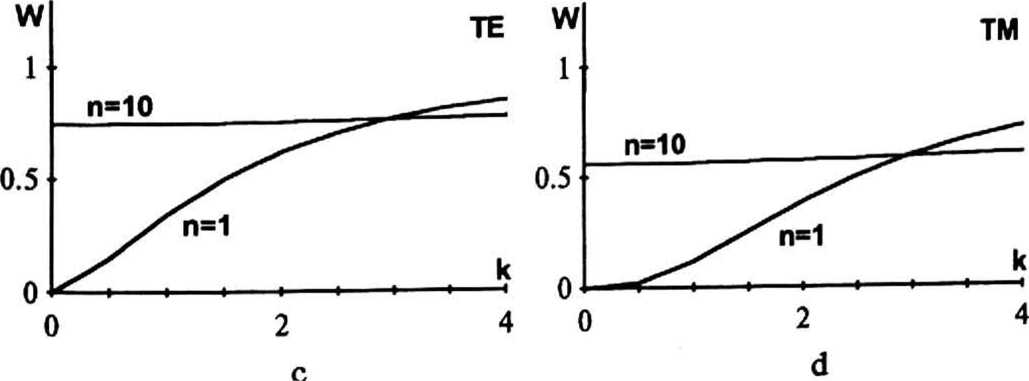
Рис.5. Зависимость энергетической эффективности от показателя преломления, коэффициента поглащения и вида поляризации.

эффективности W от показателя преломления п и коэффициента поглащения к, для горизонтальной (а, с) и вертикальной (b, d) поляризации.

Расчет производился для синусоидальной решетки высота рельефа которой Ь=0.15мкм, а период Т=100 мкм. Решетка освещается лазерным светом с длиной волны Х=0.63мкм, угол падения @1=45. На рис.5.а,Ь показаны графики зависимости энергетической эффективности от показателя преломления для различных значений коэффициента поглащения: к=0 и к=3 для поляризации ТЕ-типа (рис.5.а) и для поляризации ТМ—типа (рис.5.Ь).На pnc.5.c,d показаны графики зависимости энергетической эффективности от коэффициента поглащения для различных значений показателя преломления: п=1 и п=10 для поляризации ТЕ—типа (рис.5.с) и для поляризации ТМ—типа (pnc.S.d). Из графиков (рис.5.а,Ь) видно, что в случае прозрачного непоглащающего (п>1, к=0) материала решетки, энергетическая эффективность монотонно растет, в случае поглощающего материала (к=3) отраженная энергия слабо изменяется с ростом показателя преломления.

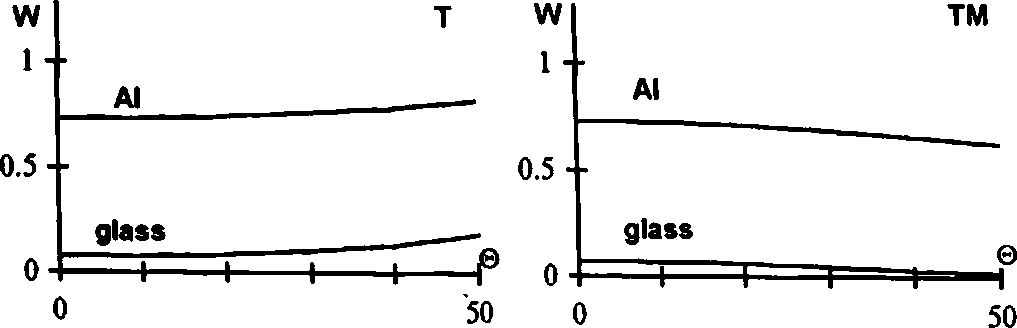
а                                       b

Рис .6. Зависимость энергетической эффективности от угла падения света в случае поляризации ТЕ и ТМ типа для решеток из разного материала.

На рис.б.а.Ь показаны графики зависимости энергетической эффективности для решеток имеющей рельеф с периодом Т= 100 мкм, высоту h=0.15 мкм и изготовленных из аллюминия и стекла, для света с длиной волны Х=0.63 мкм, в случаях горизонтальной (ТЕ) поляризациии (Рис.б.а) вертикальной (ТМ) поляризации (Рис.б.Ь). Из графиков видно, что при малых углах падения значения энергетической эффективности в случае разного типа поляризации отличаются слабо. При @i>20 градусов энергетическая эффективность начинает возрастать в случае поляризации ТЕ-типа и убывает случае поляризации ТМ-типа. Угол падения изменяется до 50 градусов.