Рассеяние света на диэлектрическом цилиндре, включающем двумерную решетку металлических наностержней

Металлические частицы с размерами от 5 нм до нескольких сотен нанометров, распределенные периодично или случайно на диэлектрической подложке, или слои таких частиц имеют интересные оптические свойства и изучались долгое время [1]. В последнее время расширились возможности по изготовлению таких систем с периодичным распределением одинаковых сфер. В зависимости от размера и распределения сфер они могут быть очень хорошими поглотителями света [2, 3] или фотонными кристаллами действующие как непоглощающие зеркала в определенном частотном диапазоне электромагнитного спектра [4].

Такие структуры являются композитными средами, включающими два и более различных материалов с характерными размерами включений, много меньшими длины волны падающего света. Для анализа подобных структур применяют теорию эффективных сред (ТЭС) в виде соотношений Мак-свелла-Гарнета [5], когда один из компонентов может рассматриваться как основной, в который встроены включения другого материала. Они предполагают точное вычисление поля в однородном основном материале, произведенного одиночным сферическим или эллиптическим включением, и модификация его с учетом взаимодействия между включениями. Теория Максвелла-Гарнета пригодна для низких концентраций (менее 30 %) относительно маленьких наночастиц (до нескольких десятков нанометров).

В работе [6] предложен метод расчета эффективной диэлектрической проницаемости композитной среды на основе детального учета запаздывания радиационного взаимодействия между составляющими среду сферическими частицами, расстояние между которыми сопоставимо с длиной волны излучения. Представленный метод позволяет рассчитывать оптические свойства композитных сред, в которых расстояние между частицами сопоставимо с длиной волны внешнего излучения. Исследования сферических серебряных включений в диэлектрическую среду показали влияние радиуса сфер и расстояний между ними на отклонение результатов теории

Максвела-Гарнета от решения, учитывающего зависимость оптических свойств металлических наношаров от их размеров. В частности, для среды с наношарами радиусом 10 нм и концентрацией 10 % отличие в результатах численного расчета показателя преломления композитного материала несущественно. Однако уже при радиусе 20 нм разница достигает нескольких десятков процентов.

В работе [7] было исследовано прохождение ТМ и ТЕ поляризованных волн в двумерных массивах серебряных наностержней различного диаметра в желатиновой среде. Авторы провели сравнение метода рекурсивных функций Грина с теорией Мак-свелла-Гарнета на примере изучения характеристик пропускания периодических и непериодических массивов наностержней. Было показано сильное влияние взаимодействия между наностержнями, вкладов мультиполей и формирования фотонных запрещенных зон на оптические спектры, что не может быть учтено в рамках классической ТЭС. Авторы отметили частичную адекватность теории Максвела-Гарнета для ТМ поляризованного света и ее непригодность для случая ТЕ поляризации.

В [8, 9] была предложена нелокальная модель однородной среды для периодичных массивов стержней с отрицательной диэлектрической постоянной на основе определения поляризуемости одиночного стержня и применения методов интегральных уравнений. Исследование модели было проведено для низких концентраций стрежней (менее 0,8 %) и малого радиуса стержней (до 12 нм для видимого диапазона). Сравнение результатов моделирования задачи отражения на конечной пластине со стержнями, ориентированными параллельно поверхности пластины, полученных с использованием нелокальной модели и электромагнитного подхода, показало адекватность подхода для ТЕ и ТМ поляризаций.

В настоящей статье проводится моделирование микроструктур, включающих массивы наностержней, объединенным методом «конечных элементов Галеркина – граничных элементов» (МКЭГ-ГЭ) [10], основанным на точной электромагнитной теории. Полученные результаты сравниваются с моделированием данных структур с усредненной диэлек- трической проницаемостью, рассчитанной в нелокальной модели однородной среды для периодичных массивов стержней с отрицательной диэлектрической постоянной. Прототипы подобных массивов были недавно изготовлены экспериментально [11, 12]. Эти массивы представляют собой упорядоченные длинные стержни из диэлектрического или металлического материала диаметром нескольких десятков нанометров.

Модель эффективной диэлектрической проницаемости

В работе [9] рассматривается матрица из диэлектрического материала с двумерной решеткой наностержней с отрицательной диэлектрической постоянной. Радиус стержней R , они расположены в квадратной сетке, расстояние между стержнями (постоянная сетки) a . Диэлектрическая постоянная стержней em . Диэлектрическая постоянная материала eh . В данной работе рассматривается распространение монохроматических полей с временной зависимостью вида e ^{+ jat} .Структура бесконечна по оси z , поэтому решение уравнений Максвелла разделяется на ТЕ (вектор электрического поля параллелен z ) и ТМ (вектор магнитного поля параллелен z ) случаи.

В [9] было показано, что для длин волн много больших радиуса стержней поле в композитной периодической структуре может быть описано с использованием нелокальной диэлектрической прони- цаемости:

eTM

2eh

Sm l fh _- 1 ^{f S}m ^{- S}h

^STE ( ® , ^kz )   ^Sh ⁺

___________Sh___________

Sh в - kz

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^™  ^^^^^^»  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^™

(^Sm — ^Sh ) ^{f    в}Р

где e_TM , e_TE - диэлектрические проницаемости для ТМ и ТЕ поляризаций, f = nR ²/ a ² - концентрация стержней, kz - z -компонента волнового вектора, в = rn^ehy - волновое число в диэлектрической структуре, в_р - плазменное волновое число для идеально проводящих стержней приводится в [8]:

2 п

^{( в}Р^{а )2} "

ln | — | + 0,5275 ( 2 nR )

Заметим, что в [8, 9] ур. (1) для еТМ приводится только для стационарного предела ( k = 0 и в = 0), тогда как ур. (2) для еТЕ выводится для динамического случая. Воспользовавшись вычислениями авторов в [8], запишем выражение для еТМ для динамического случая:

^eTM ⁽®^{) e}h ⁺

Sh

• ^{1   S}m ^{+ S}h   ^{в 2} .

^^^^^^^^^^^^^^^^^_ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^.  ^^^^^^В  ^^^^^^^^^^^^^^^^_

• 2    f е - е  вг

mh  p

Из ур. (2) и (4) следует, что среда обладает пространственной дисперсией. Так, диэлектрическая проницаемость зависит не только от частоты падающего света в , но и от компонента волнового вектора, параллельного стержням. Предложенная модель также действует для диэлектриков с положительной вещественной частью диэлектрической проницаемости.

Массивы наностержней в диэлектрическом цилиндре

Для проверки предложенной модели эффективной диэлектрической проницаемости мы рассмотрим рассеяние плоской волны с длиной волны 0,5 мкм на диэлектрическом цилиндре с серебряными стержнями. Как показано на рис. 1, стержни находятся в цилиндре круглого сечения с диэлектрической проницаемостью e_h = 2,25. Радиус цилиндра во всех экспериментах был принят равным 0,5 мкм. Материал стержней - серебро ( e_m = - 9,49 + 1,483i). Для простоты мы ограничимся случаем падения волны с kz = 0.

,.»’               ,<<00 О О ООХ

/О о о о о о о о оХ /ооооооооооХ /ооооооооооооХ / о о о о о о о о о о о о \

S/          р о о о о о о о о о о о о а booooooooooood 1000000000000/ \pooooooooooo/ к""'          \ оооооооооо /

----------► ХЭ о о о о о о о о у о о о о

Рис. 1. Массивы наностержней в диэлектрическом цилиндре, бесконечно простирающемся по оси z

Далее, для демонстрации точности теоретических результатов, проведена серия численных экспериментов моделирования дифракции света на структуре с представленной геометрией с вариацией значений концентрации стержней f от 0 до 1 и вариацией значений радиуса стержней от 5 нм до 30 нм. Содержание стержней 100 % соответствует полностью металлическому цилиндру, содержание 0 % -полностью диэлектрическому. Выбор значений радиуса стержней был продиктован значительным отличием поляризационных характеристик маленьких и больших наночастиц [13]. Если наночастица достаточно мала (R << Х0, где Х0 - длина волны падающего света), то, в соответствии с теорией Ми, вклад в спектр поглощения дают только дипольные плазмонные колебания. Тогда как, для больших частиц вклад в спектр дают также и резонансы высокого порядка. Когда наноразмерная частица освещается светом, электрическая компонента электромагнитного поля возбуждает коллективные колебания электронной плазмы внутри частиц - плазмоны. Если частицы расположены в цепочки эти плазмонные колебания принимают резонансный характер, что облегчает прохождение волн резонансных частот. Такие цепочки исследовались в литературе [9, 14] как потенци- альные кандидаты для субволнового волноводного распространения света.

Эффективная диэлектрическая проницаемость рассчитывалась по формулам (2) и (4). Объединенным методом МКЭГ-ГЭ проводилось моделирование дифракции плоской волны на цилиндре с вычисленной эффективной диэлектрической проницаемостью. С другой стороны, этим же методом также моделировалась дифракция на структуре с детальной геометрией стержней. Для оценки дифракционного рассеяния использована диаграмма направленности рассеяния, зависящая от угловой координаты ф и определенная в бесконечно удаленных точках ( l ^ да) как с ( ф ) = lim 2nl | usc | 2 /1 u™ |², где usc и и™ - рассеянное и падающее поля. В частности, рассеяние определялось в прямом ( ф = 0°), в обратном ( ф = 180°) и в поперечном направлениях ( ф = 90°).

ТЕ поляризация

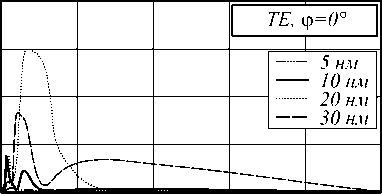
Рассмотрим прохождение ТЕ поляризованного света через структуру с геометрией, представленной на рис. 1. На рис. 2 представлены зависимости от концентрации f отношения значений рассеяния TE волн с к значениям рассеяния с₀ диэлектрического цилиндра для расчетных углов ф для стержней радиусом 5, 10, 20, 30 нм.

ст/стп

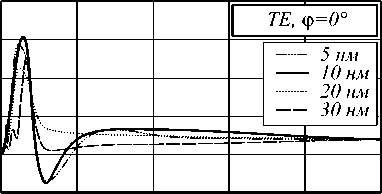
чие распределений для стержней различных радиусов. В диапазоне концентрации от 6 % до 20 % с увеличением радиуса стержней наблюдается увеличение рассеяния вперед в несколько раз. Рассеяние в поперечном направлении для стержней радиусом 5, 10 и 20 нм и концентрацией от 6 % до 12 % существенно снижается, для стержней радиусом 30 нм в данном диапазоне концентрации наблюдается обратная зависимость. Рассеяние в обратном направлении для стержней радиусом 5 и 10 нм имеет минимумы на концентрациях 3 и 11 %. Минимумы смещаются на концентрации 3 и 7 % соответственно для радиуса стержней 20 нм и 3 и 6 % для радиуса 30 нм.

На рис. 3 представлены зависимости от концентрации f отношения отклонений А с значений рассеяния TE волн с от значений ceff , рассчитанных на основе эффективной диэлектрической проницаемости, к значениям рассеяния с0 диэлектрического цилиндра для расчетных углов ф . По представленным зависимостям можно отметить рост значений отклонений с ростом радиуса стержней на всем диапазоне концентраций. Неравномерность роста можно объяснить резонансными эффектами, связанными с взаимодействием плазмонов в стержнях и зависящих от расстояния между ними.

Аст/Ь,,

1,5

0,5

1,0

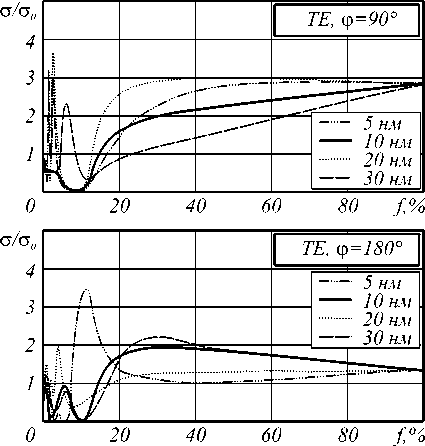
Рис. 2. Зависимость рассеяния ТЕ волны на структуре точной геометрии от концентрации стержней f

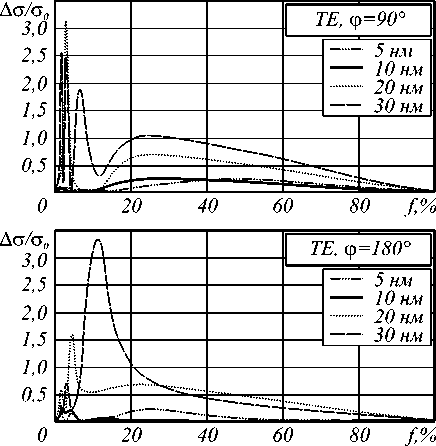
Рис. 3. Зависимость от концентрации стержней f отклонений рассеяния ТЕ волны на структуре точной геометрии от отклонений рассеяния на структуре с эффективной диэлектрической проницаемостью

Рассматривая зависимости рассеяния в прямом направлении можно отметить незначительное отли-

На рис. 4 представлены зависимости от концентрации f относительных отклонений А с значений рассеяния TE волн с от значений cef , рассчитанных на основе эффективной диэлектрической проницаемости.

представлены зависимости от концентрации f отношения значений рассеяния ТМ волн с к значениям рассеяния с₀ диэлектрического цилиндра для расчетных углов ф .

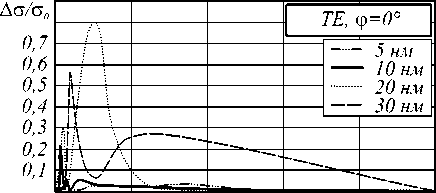
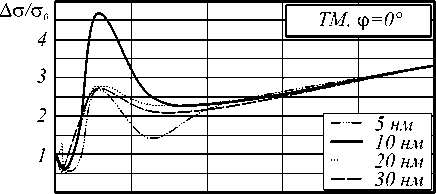
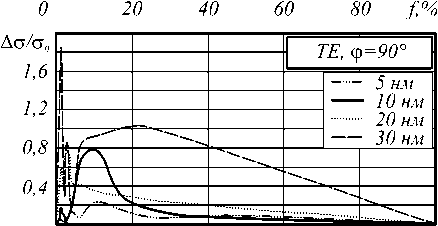
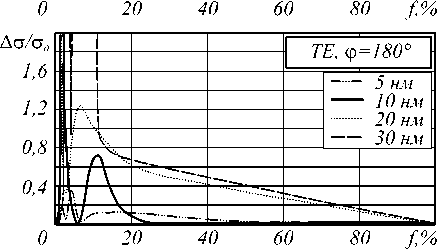
Рис. 4. Зависимость от концентрации стержней f относительных отклонений рассеяния ТЕ волны на структуре точной геометрии от отклонений рассеяния на структуре с эффективной диэлектрической проницаемостью

Среднее по концентрации относительное отклонение представлено в таблице:

Радиус стержней	Направление рассеяния
	ф = 0 °	ф = 90 °	Ф = 180 °
5 нм	1 %	8 %	5 %
10 нм	2 %	16 %	13 %
20 нм	11 %	19 %	41 %
30 нм	15 %	60 %	579 %

Таким образом, из сводной таблицы следует, что для случая прохождения ТЕ волны через массив металлических стержней в диэлектрической структуре рассматриваемая нелокальная модель однородной среды адекватно описывает среду со стержнями радиусом R < Х 0 /50.

ТМ поляризация

Рассмотрим прохождение ТМ поляризованного света через рассматриваемую структуру. На рис. 5

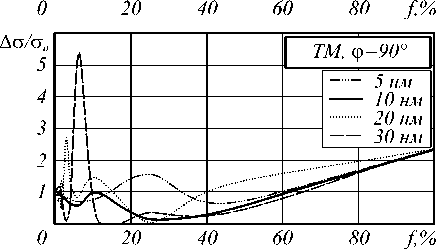
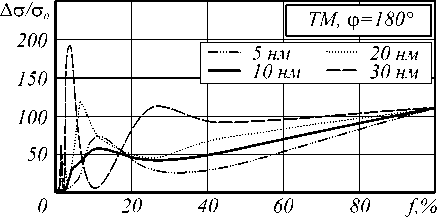
Рис. 5. Зависимость рассеяния ТМ волны на структуре точной геометрии от концентрации стержней f

Зависимости рассеяния в прямом направлении слабо отличаются для радиусов 5, 20 и 30 нм. Рассеяние в поперечном направлении для радиуса стержней 5 нм не имеет резонансных экстремумов. Для R > 20 нм появляются ярко выраженные минимумы на порядок меньшие рассеяния диэлектрической структуры. Рассеяние назад для металлической структуры на два порядка больше рассеяния назад диэлектрической структуры. При увеличении радиуса стержней до 30 нм в зависимости рассеяния назад от концентрации появляются минимумы одного порядка с рассеянием на диэлектрической структуре.

На рис. 6 представлены зависимости от концентрации f отношения отклонений Ag значений рассеяния ТМ волн g от значений c_eff, рассчитанных на основе эффективной диэлектрической проницаемости, к значениям рассеяния с0 диэлектрического цилиндра для расчетных углов ф. По представленным зависимостям не отмечается явная зависимость значений отклонений от радиуса стержней.

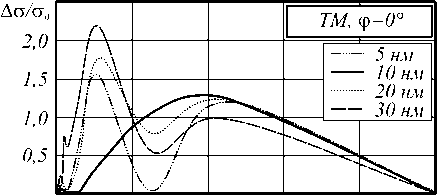
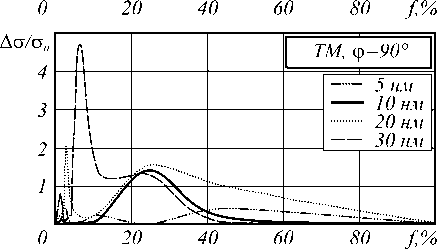
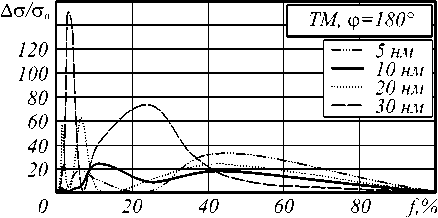
Рис. 6. Зависимость от концентрации стержней f отклонений рассеяния ТМ волны на структуре точной геометрии от отклонений рассеяния на структуре с эффективной диэлектрической проницаемостью

На рис. 7 представлены зависимости от концентрации f относительных отклонений А с значений рассеяния ТМ волн с от значений of, рассчитанных на основе эффективной диэлектрической проницаемости.

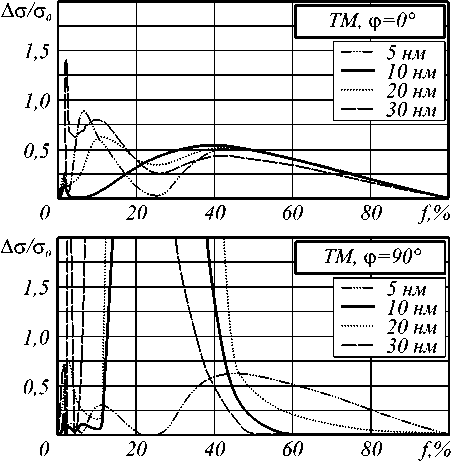
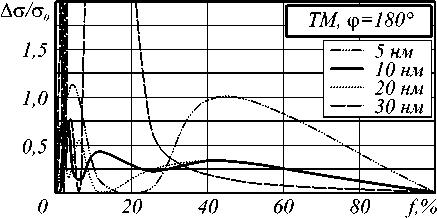
Рис. 7. Зависимость от концентрации стержней f относительных отклонений рассеяния ТМ волны на структуре точной геометрии от отклонений рассеяния на структуре с эффективной диэлектрической проницаемостью

Среднее по концентрации относительное отклонение представлено в таблице:

Радиус стержней	Направление рассеяния
	ф = 0 °	ф = 90 °	ф = 180 °
5 нм	29 %	27 %	50 %
10 нм	28 %	162 %	23 %
20 нм	33 %	483 %	21 %
30 нм	34 %	169 %	106 %

Среднее относительное отклонение рассеяния для случая прохождения ТМ волны заметно больше среднего относительного отклонения в случае прохождения ТЕ волны. Можно отметить, что для концентраций f < 1 % среднее отклонение не превышает 10 %, если радиус стержней меньше 20 нм.

Таким образом, рассматриваемая нелокальная модель однородной среды не может адекватно описать резонансные процессы высокого порядка, происходящие в стержнях большого радиуса. Также стоит отметить, что учет взаимодействия между наностержнями, осуществленный в модели, не полностью описывает реальные процессы. В случае малых концентраций стержней и, соответственно, большого расстояния между ними расчеты показывают низкое отклонение. С уменьшением расстояния между стержнями, погрешность увеличивается.

Заключение

В работе рассмотрена задача распространения ТМ и ТЕ поляризованного света в двумерных массивах серебряных наностержней различного радиуса и концентрации в диэлектрической структуре. Сравнение точных численных результатов с расчетами на основе нелокальной модели однородной среды для периодичных массивов стержней с отрицательной диэлектрической постоянной было проведено объединенным методом МКЭГ-ГЭ. На основе сравнения были установлены границы применимости нелокальной модели.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-SA-06), и грантов РФФИ №№05-08-50298, 07-07-97600 и 08-07 99007.