Расширение корональных выбросов массы в поле зрения SOHO / LASCO: некоторые закономерности

Видимый угловой размер (будем обозначать его 2 a ) коронального выброса массы (КВМ) является его геометрической мерой и одновременно отражает важные физические свойства КВМ, такие как масса и кинетическая энергия. Вблизи поверхности Солнца значительная часть КВМ движется с возрастающим угловым размером. Так, по данным наземных коронографов «Mark-3» и «Mark-4» ( R <  2.45(2.9) R о ), доля таких КВМ составляет около одной трети [1]. Здесь R – расстояние в картинной плоскости от центра солнечного диска, R ʘ – радиус Солнца, число в скобках относится к «Mark-4».

В ряде исследований сделан вывод, что угловой размер движущихся КВМ может изменяться и на расстояниях R > (2.5 ^ 3) R о [2-4] (нерадиальное расширение по терминологии [2]). Согласно [2], угловые размеры многих КВМ, зарегистрированных в поле зрения коронографа «SOLWIND», в первые два часа их наблюдения увеличиваются в два раза и более. По данным [2], угловые размеры большинства рассмотренных приэкваториальных КВМ, наблюдавшихся в поле зрения LASCO C3 ( R = (3.7 ^ 32) R о ), возрастают по мере движения КВМ. При этом максимальное увеличение угловых размеров КВМ по сравнению с радиальным расширением составило ~5-6.5 ° в области одной «ноги» КВМ, т. е. оказалось относительно небольшим. Существование КВМ (данные LASCO), угловые размеры которых увеличиваются со временем, было отмечено в [4]. С другой стороны, нередко исследователи полагают, что изменения угловых размеров КВМ в поле зрения LASCO пренебрежимо малы. Таким образом, ясных представлений о вариациях угловых размеров КВМ со временем при R >(2.5 ^ 3) R о в данный момент нет.

В настоящей работе по данным инструментов LASCO C2 и C3 исследованы закономерности расши- рения КВМ, связанных с эруптивными протуберанцами и/или постэруптивными аркадами на лимбе.

Данные и метод анализа

Для определения характеристик КВМ использовались данные SOHO/LASCO двух типов: некалиброванные разностные изображения короны из базы данных и калиброванные изображения короны с уровнем обработки изображений L1, в которых минимизировано влияние различных искажений изображений.

В большинстве случаев наблюдаются относительно небольшие изменения угловых размеров КВМ 2a со временем (расстоянием). Поэтому необходимо обеспечить как можно большую точность определения значений 2a. Хотя определение угловых размеров КВМ выполнялось многими исследователями и практически превратилось в рутинную операцию, нахождение этих размеров с точностью < 3° (иногда достаточно 5°) является весьма непростой задачей. Существуют следующие причины, которые ограничивают точность нахождения 2a: 1) маленький градиент яркости в области границы КВМ; 2) вариации яркости фоновой плазмы или предшествующего выброса корональной массы вблизи границы КВМ; 3) незначительное превышение яркости КВМ вблизи его границы над яркостью окружающего фона. Чтобы обеспечить определение размеров КВМ с указанной точностью, значения 2a находились с помощью двух дополняющих друг друга методов. В первом случае угловой размер КВМ определялся как угол между двумя лучами, проведенными из центра солнечного диска в картинной плоскости к граничным особенностям КВМ. Для выделения этих особенностей использовались последовательности во времени разностных изображений короны. Такие изображения получаются в результате вычитания из изображения короны, зарегистрированного в фиксиро- ванный момент времени, ее изображения в предшествующий момент. Во втором случае угловой размер КВМ находился с помощью сканов по широте яркости изображений короны с уровнем обработки L1.

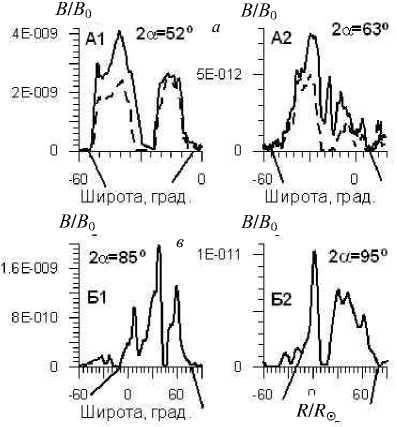
На рис. 1 приведены примеры определения величины 2 а первым методом как для случаев, когда границу КВМ практически без труда можно выделить достаточно точно (рис. 1, а , б ), так и для проблемных с точки зрения нахождения границы КВМ ( в , г ). В первом случае точность нахождения 2 а может быть до 3-5 ° . Во втором случае точность нахождения угловых размеров КВМ может превышать 5 ° .

Рис . 1. Примеры определения угловых размеров КВМ на фоне различных факторов , затрудняющих нахождение границ КВМ : а, б – КВМ с относительно резкими грани цами или с особенностями на границе , позволяющими относительно точно определять угловые размеры КВМ с точностью до ~3 ° ; в - КВМ с маленьким градиентом ярко сти в области границы ; г – вариации яркости предшест вующего выброса корональной массы вблизи границы КВМ затрудняют ее однозначное выделение .

б

г

Рис . 2. Примеры нахождения угловых размеров КВМ с помощью разностных сканов яркости калиброванных изо бражений с уровнем обработки L1. Отрезками показаны гра ницы КВМ : а – 02.06.1998 (10:29–07:02), W- лимб , R = 3 R ʘ ; б – 02.06.1998 (13:44–08:47), W- лимб , R = 14 R ʘ ; в – 07.01.2001 (5:29–3:53), W- лимб , R =3 R ʘ ; г – 07.01.2001 (9:17–5:17), W- лимб , R =10 R ʘ . В скобках рядом с датами указаны мо менты времени , для которых производилось вычитание одного изображения короны из другого . Для сравнения приведены сканы яркости на двух радиусах ( сплошная и штриховая линии ), один из которых указан в скобках (а, б).

На рис. 2 показаны примеры нахождения угловых размеров КВМ с помощью сканирования по широте яркости разностных изображений короны. Заметим, что в этом случае производилось еще и усреднение яркости по широте, чтобы уменьшить шумовую составляющую сигнала. Из рис. 2 следует, что в приведенных примерах границы КВМ отчетливо выделяются как места, где яркость после сильного спада в теле КВМ д остигает нулевого или минимального значения.

В данной работе для анализа была отобрана группа из 48 лимбовых КВМ, которые были зарегистрированы коронографами LASCO в 1997–2002 гг. и связаны с лимбовыми эруптивными протуберанцами и/или постэруптивными аркадами [5, 6]. Критерии отбора событий даны в [5]. Выбор КВМ такого типа обусловлен тем, что, предположительно, для них влияние проекционных эффектов, искажающих видимые размеры КВМ, минимально.

Результаты

На рис. 3 показаны примеры характерных изменений угловых размеров КВМ в зависимости от положения их фронта ( R _F). Первое нахождение величины 2 а производилось в первый момент, когда можно было определить истинный угловой размер КВМ. Визуальный анализ всех рассмотренных зависимостей 2 a ( R F ) показывает, что, начиная с некоторого значения R F , которое будем обозначать R _am , угловой размер КВМ достигает своего максимального значения 2 a m . Далее этот размер перестает меняться, либо меняется очень слабо в пределах погрешности ~3 ° , либо начинает уменьшаться.

Установлено, что имеется положительная корреляция между Ram и 2am, причем связь между этими параметрами становится более сильной для относительно медленных КВМ (рис. 4). Связь между Ram и скоростью фронта КВМ VF (здесь не приводится) оказывается слабой и возрастает для КВМ с относительно небольшими угловыми размерами 2am. В качестве VF принималась скорость из каталога , которая получается при линейной аппроксимации RF(t).

Увеличение углового размера КВМ 2 a при движении КВМ может быть обусловлено разными причинами. Чаще всего это связано с более быстрым, чем в случае 2 a = const, увеличением поперечных линейных размеров КВМ. В некоторых случаях нерадиальное расширение КВМ связано с уширением основания КВМ на границе искусственной луны. В третьем случае речь идет о КВМ, для которых увеличение угловых размеров обусловлено одновременным действием этих двух механизмов. Особым оказался КВМ, зарегистрированный 13.07.1999 г. Со временем этот КВМ искривляется, отклоняясь от радиального направления, что и приводит к кажущемуся сильному увеличению угловых размеров. Для этого КВМ мы использовали его реальные угловые размеры.

Сравним некоторые свойства КВМ с радиальным и нерадиальным расширением. Во вторую группу мы отобрали лишь те КВМ, увеличение угловых размеров которых связано с дополнительным расширением за счет увеличения поперечных линейных размеров. Результаты сравнения характеристик КВМ

В . Г . Файнштейн

2а, град

$7.04

град.

Н2ЙО2г.

Рис . 3. Примеры характерных изменений угловых раз меров КВМ в зависимости от положения их фронта ( R _F). Цифры рядом с кривыми – даты КВМ .

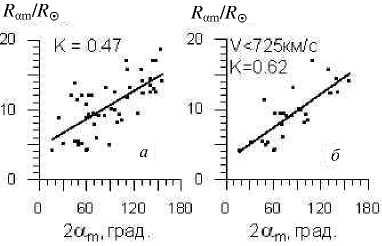
Рис . 4. Зависимость R _{a m} от максимального углового раз мера КВМ 2 a m ( а ); зависимость R _{a m} (2 a m, ) для КВМ со ско ростями V _F< 725 км / с ( медианное значение скорости ) (б). K – коэффициент корреляции .

двух типов можно выразить следующими числами: средний угловой размер радиально расширяющихся КВМ равен 64.9 ° (29.1 ° ), нерадиально расширяющихся - 92.4 ° (36.8 ° ). Соответствующие значения средней скорости: 468(240.9) и 781(254) км/с. Числа в скобках – среднеквадратичные отклонения.

Оказалось также, что КВМ второго типа являются более яркими и более плотными на больших расстояниях (рис. 5). Показаны радиальные сканы калиброванной яркости двух КВМ вдоль радиусов вблизи осей КВМ. Отрезками показаны максимальные значения яркости во внешних оболочках (фронтах) КВМ.

Заметим, что яркость внешней части КВМ с неизменными угловыми размерами практически не превышает уровень шума, когда фронт КВМ находится вблизи внешней границы поля зрения коронографа LASCO C3 ( R = (25 ^ 30) R _о ). В то же время яркость внешней оболочки нерадиально расширяющихся КВМ может превышать шум примерно в 3–10 раз. Из примеров на рис. 5 следует, что яркость K-короны во фронте нерадиально расширяющегося КВМ ( а , б ) примерно в 6 раз больше по сравнению с радиально расширяющимся КВМ ( в , г ). Учитывая, что угловой размер КВМ первого типа в среднем примерно в 1.5 раза (см. выше) больше размеров КВМ второго типа, мы приходим к выводу, что концентрация электронов и, в целом, плотность плазмы в таких КВМ в несколько раз больше, чем в КВМ с радиальным расширением. Это дает основание предположить, что физической причиной нерадиального расширения КВМ является повышенное давление плазмы внутри внешней оболочки КВМ по сравнению с фоновой плазмой.

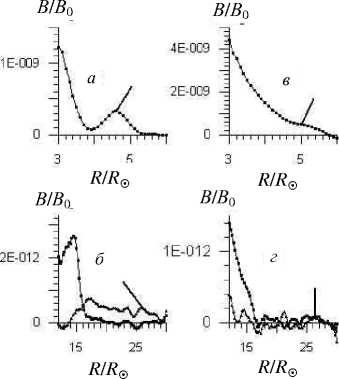
Рис . 5. Радиальные сканы калиброванной яркости для КВМ с нерадиальным (а, б) и радиальным расширением (в, г); а – С 2, 07.01.01, 05:29–03:53; б – С 3, 07.01.01, 09:17– 05:17, кружки , 13:41–05:17, треугольники ; в – С 2, 25.11.97, 20:23–19:30; г – С 3, 25.11.97, 06:42–00:18, кружки , 08:42– 00:18, треугольники . Рядом с датами регистрации КВМ указаны моменты времени , для которых производилось вычитание одного изображения короны из другого .

В заключение сделаем одно замечание. В данном исследовании видимый угловой размер КВМ определялся как величина угла с вершиной в центре солнечного диска, а под расширением КВМ понималось увеличение этого угла. Такое определение углового размера КВМ является общепринятым (см. [1–4] и ссылки там). В то же время вершину угла, определяющего размер КВМ, можно, в принципе, поместить в любое другое место. Существуют исследования, в которых эту вершину помещают, например, на поверхность Солнца на оси КВМ (в условное место возникновения КВМ). Легко убедиться, что это приводит к изменению характера зависимости 2 a ( R F ) по сравнению со случаем, когда вершина угла помещается в центре солнечного диска. Например, угловые размеры КВМ, которые рассматривались в данной работе как радиальные, будут уменьшаться с ростом R _F. В то же время, как нетрудно показать, и в этом случае рассмотренные КВМ могут быть разбиты на два класса. Но критерии отнесения КВМ к тому или иному классу изменятся. При этом к одному новому классу будут отнесены все те КВМ, которые входили в группу радиальных КВМ, к другому классу – входившие в группу нерадиальных КВМ из данного исследования. Более детально этот вопрос будет рассмотрен в полной версии работы.

SOHO является продуктом международной кооперации ESA и NASA. Работа выполнена при поддержке правительственного гранта финансовой поддержки ведущих научных школ РФ № НШ 4741.2006.2 и Программы фундаментальных исследований Президиума РАН № 16.