Расстояние бездифракционного распространения ограниченного пучка Эйри

Как известно, пучки Эйри [1, 2] обладают бесконечной энергией, и поэтому при распространении по параболе сохраняют свою интенсивность, то есть распространяются бездифракционно. Но на практике приходится либо ограничивать пучок Эйри в начальной плоскости конечной апертурой [3], либо аподизировать его экспоненциальной [2] или гауссовой функцией [4]. При этом пучок Эйри на начальном участке своей траектории сохраняет свои замечательные свойства (безди-фракционность, распространение по параболе и самовосстановление при искажении) до определённого расстояния, а затем начинает расходиться, и амплитуда в главном максимуме начинает убывать до нуля. В работе [3] было показано, что пучок Эйри, ограниченный по апертуре, значительно меньше подвержен дифракции, чем пучок Эйри, усечённый функцией Гаусса либо экспоненциально. Целью данной работы является получение формулы для определения максимального расстояния по оптической оси (начиная от начальной плоскости), на котором ограниченный по апертуре пучок Эйри сохраняет свойство инвариантности.

координату x = –Δ x , при другом значении z из уравнения (2) будет иметь координату x = 0. То есть если мы будем считать Δ x = R модулем координаты края диафрагмы (далее эту величину будем называть радиусом диафрагмы), ограничивающей на отрицательной части оси пучок Эйри

E ( x , z = 0) =

Ai ( x/x ₀ ) , x > - R , 0, x <- R ,

то из (2) найдём выражение для расстояния z 1 , за которое точка с координатами ( x = –R, z =0) (край диафрагмы) сместится в точку с координатами ( x = 0, z = z 1 ) (оптическая ось):

z 1 = 2 kx 0/2

R .

При выводе (4) мы неявно предполагали, что луч, вышедший из начальной точки с координатами ( x =– R, z = 0), пересечётся с параболической траекторией главного максимума пучка Эйри в точке с координатами ( x = R, z ). Далее мы докажем эту гипотезу и

1. Получение расстояния инвариантности

из уравнения траектории

Пучок Эйри описывается комплексной амплитудой [1, 2]:

Г    £2)

E (5, £) = Ai I 5 - — I exp

i

Г £\ 5 £ )

I 12 2 J

где s = x/x 0 – безразмерная поперечная координата вдоль оси x , x 0 - масштаб функции Эйри Ai( x ), £ = z /( kx 02 ) -безразмерная продольная координата вдоль оптической оси z , k = 2π/λ – волновое число света с длиной волны λ. Пучок (1) распространяется по параболической траек-

покажем, что это расстояние z 1 и есть расстояние инвариантности пучка Эйри. На рис. 1 показано распределение интенсивности в плоскости Oxz для разных значений радиуса диафрагмы. Из рис. 1 видно, что траектория главного максимума образует каустику, причём луч, выходящий из крайней точки диафрагмы ( x = - R , z = 0), распространяется под углом в к оптической оси и является касательным к каустике (рис.

1 б) . Найдём угол в , предполагая, что R > 0.

Очевидно, траектория главного максимума, описываемая формулой (2), и прямая, соответствующая лучу, вышедшему из крайней точки диафрагмы под углом в , должны пересекаться ровно в одной точке. Поэтому дискриминант квадратного уравнения

тории, которая описывается уравнением:

Ax =

4 k ² x ₀ ³

где Δ x – поперечное смещение точки пучка Эйри, которая была в начале координат ( x = z = 0). Из (2) следует, что точка пучка Эйри, которая при z = 0 имела

2 z

4 k ² x ₀ ³

= - R + z tg в

должен быть равен нулю:

D = tg² в- 4

1 4 k ² x ₀ ³

R = 0,

т.е. tg в = RR-J ( kx 32 ) .

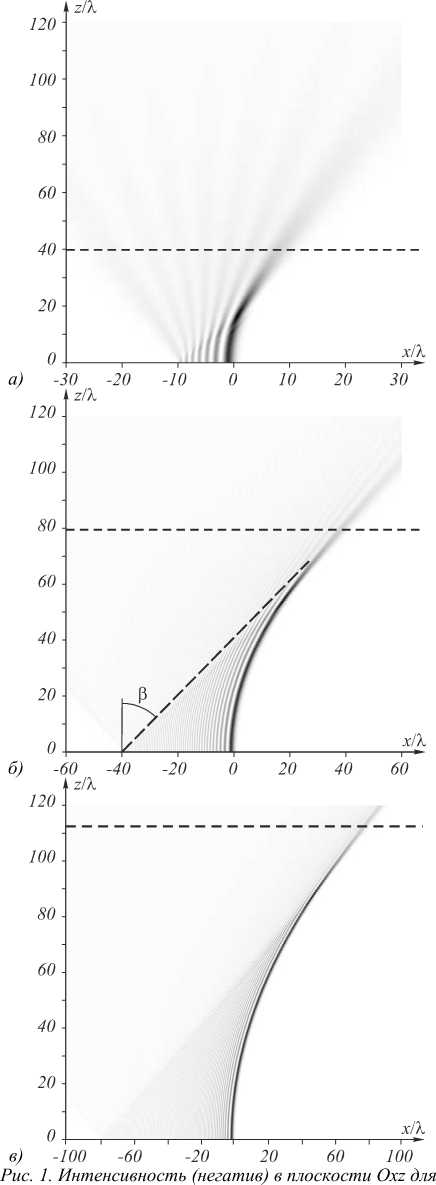
радиусов диафрагм R = 10 Л (а), R = 40 Л (б) и R = 80 Л (в).

Горизонтальной прерывистой линией показана длина инвариантности пучка Эйри, вычисленная по формуле (4)

является пучок Бесселя, который на практике также сохраняет свою инвариантность на некотором расстоянии, зависящем от радиуса круглой диафрагмы R . Сравним выражение (4) с аналогичным выражением [5] для ограниченного пучка Бесселя J 0 ( kr sin θ):

z max

R tg 6,

где r – радиальная координата, θ – угол наклона конической волны, формирующей пучок Бесселя , J ₀( x ) – функция Бесселя нулевого порядка. Из (5) видно, что длина инвариантности для ограниченного пучка Бесселя пропорциональна радиусу апертуры R , а аналогичная длина инвариантности пучка Эйри (4) пропорциональна корню квадратному из R . То есть при прочих равных условиях пучок Бесселя будет оставаться бездифракцион-ным на большем участке траектории, чем пучок Эйри.

2. Получение расстояния инвариантности из асимптотики фазы пучка Эйри

Функция Эйри из (1) при больших (по модулю) отрицательных значениях аргумента s << –1 имеет асимптотику (выражение 10.4.60 в [6]), из которой следует, что

s

Ai(-s) ~---^х

2 /

х

I ² 3/2 exp i s ^3/2

I 3

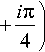
2 3/2 exp - / s

I 3

/ п

-

Поле с комплексной амплитудой (6) представляет собой суперпозицию двух полей с противоположными по знаку фазами. Фаза второго поля равна

Ф ( s ) = - 3 s ^3/2.

Асимптотика (7) была использована в [7] для формирования пучка Эйри с помощью жидкокристаллического модулятора света. Используем выражение (7), чтобы получить формулу для расчёта расстояния инвариантности ограниченного пучка Эйри. Световой луч, приходящий с начальной плоскости из точки с координатами ( x = sx ₀, z = 0) в точку траектории пучка Эйри с координатами (Δ x, z ), определяется производной фазы (7)

1 dx

--ф(s) =3-2 k dxkx

Производная фазы (8) равна тангенсу угла накло-

на ф луча к оси z :

1d у—ф( s)

k dx

= tg ф .

Само расстояние при этом равно корню данного квадратного уравнения:

z max

tg в

2/ ( 4 к² х О )

= 2 кх ₀ ^3/2 JR ,

т.е. получилось расстояние, совпадающее с (4).

Бездифракционный пучок Эйри является двумерным. В трёхмерном случае бездифракционным пучком

С другой стороны, тангенс (9) равен отношению суммы расстояния от начала координат до точки начала луча x = sx ₀ и смещению Δ x (2) к расстоянию z до точки наблюдения на траектории пучка Эйри:

tg ф=

х + Ах

z

Приравнивая правые части (8) и (10), получим:

z = 2 кх ₀ ^3/2

x .

Пусть расстояние x равно модулю координаты конца диафрагмы, ограничивающей в начальной плоскости пучок Эйри x = R , тогда получим формулу для расстояния инвариантности ограниченного пучка Эйри:

z ₂ = 2 kx ₀ ^3/2 R . (12)

Первое слагаемое в (6) соответствует полю, лучи которого направлены в противоположную сторону (симметрично относительно оптической оси). Эти лучи пересекаются только в области отрицательных значений z , т.е. образуют мнимую каустику, поэтому вклад от данного поля не влияет на расстояние инвариантности ограниченного пучка Эйри.

Сравнивая (4) и (12), заключаем, что оба выражения, полученные разными способами, для длины инвариантности ограниченного с одной стороны пучка Эйри равны z 1 = z 2 . В [8] исследован вопрос соответствия лучей, выходящих из начальной плоскости пучка Эйри, точкам параболической траектории главного максимума. Но выражения типа (4), (12) в [8] не были получены.

• 3.    Результаты моделирования

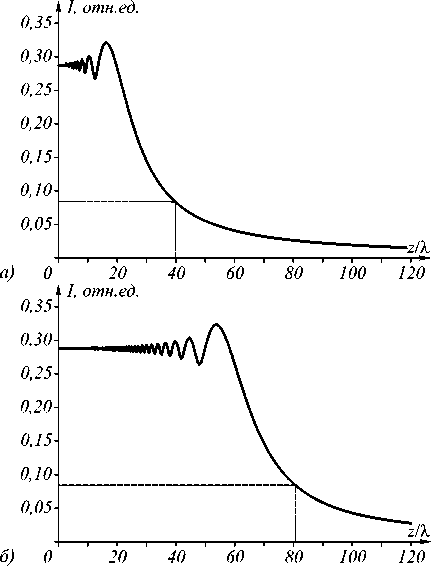
На рис. 2 показаны зависимости максимальной интенсивности ограниченного пучка Эйри (3) от пройденного расстояния z для различных значений радиуса диафрагмы R : 10 λ (а), 40 λ (б), 80 λ (в).

Определим длину ограниченного пучка Эйри как расстояние, на котором максимальная интенсивность спадает до некоторого уровня. Чтобы определить этот уровень, рассмотрим по аналогии ограниченный пучок Бесселя с комплексной амплитудой в начальной плоскости J ₀( r / r ₀)circ( r / R ) ( r – радиальная полярная координата, circ( x ) – функция круга, равная единице при x ≤ 1 и равная нулю при x > 1).

При λ = 532 нм, R = 10 λ и r ₀ = λ длина пучка Бесселя согласно формуле (5) равна z max = R [( kr 0 )² – 1]^1/2 ≈ 33 мкм=62 λ . Численное моделирование показало, что на этом расстоянии осевая интенсивность Бесселева пучка составляет 16% от начальной интенсивности (рис. 3). Из рис. 3 видно, что на расстоянии z max зависимость осевой интенсивности от расстояния z не имеет никаких характерных особенностей. Так, например, она не является точкой максимума или минимума, а также не является точкой полуспада интенсивности от начального уровня. По аналогии определим условно длину пучка Эйри так, чтобы для какого-либо определённого радиуса диафрагмы эта длина совпала с расчётным значением, вычисленным по формуле (4).

Выберем этот радиус диафрагмы равным R = 10 λ . Длина такого ограниченного пучка Эйри согласно (4) равна z _max ≈ 39,7 λ . Интенсивность пучка на этом расстоянии, рассчитанная BPM-методом, составляет 29,3% от начального уровня. Далее для всех других радиусов диафрагм определим длину пучка как расстояние, на котором интенсивность спадает до 29,3% (рис. 2). На рис. 4 показана зависимость расстояния инвариантности ограниченного пучка Эйри от радиуса диафрагмы, вычисленная по формуле (4) и BPM-методом.

Моделирование показало, что при малом радиусе диафрагмы теоретическое и расчётное расстояния инвариантности существенно отличаются, однако при R ≥ 10λ ошибка составляет менее 5%.

I, отн.ед.

0,35-

0,30-

0,25-

**vvvvVVV\/^

0,20-

0,15-

0,10- fl,05- z/X

в)    0

20    40    60    80    100   120

Рис. 2. Зависимости максимальной интенсивности ограниченного пучка Эйри (3) от пройденного расстояния z для различных значений радиуса диафрагмы R: 10 λ (а), 40 λ (б), 80 λ (в)

Заключение

В работе получено явное выражение, определяющее расстояние инвариантности ограниченного пучка Эйри, т.е. расстояние, на котором пучок Эйри, ограниченный в начальной плоскости со стороны медленного убывания амплитуды, распространяется по параболической траектории без изменения амплитуды (почти без дифракции). Это расстояние получено двумя способами – из уравнения траектории и из распределения фазы пучка Эйри. В отличие от аналогичного расстояния для бездифракционного пучка Бесселя, пропорционального радиусу ограничивающей пучок круглой диафрагмы, расстояние инвариантности для пучка Эйри пропорционально корню квадратному от координаты края (по абсолютной величине) ограничивающей диафрагмы. Для пучка Бесселя это расстояние не зависит от длины волны света, в то время как для пучка Эйри оно обратно пропорционально длине волны. При прочих равных условиях расстояние инвариантности для пучка Эйри меньше, чем для пучка Бесселя.

Uh

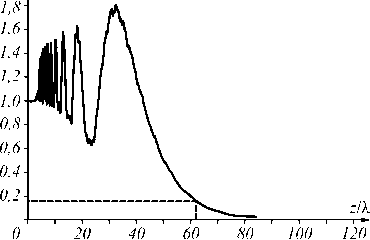
Рис. 3. Зависимость максимальной (осевой) интенсивности ограниченного пучка Бесселя от пройденного расстояния z (R = 10 λ ). Пунктирной линией обозначены расстояние

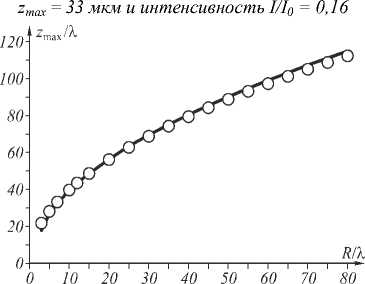
Рис. 4. Зависимость расстояния инвариантности ограниченного пучка Эйри от радиуса диафрагмы, вычисленная по формуле (4) (сплошная кривая) и BPM-методом (кривая, заданная точками)

Работа выполнена при поддержке грантов Президента РФ поддержки ведущих научных школ (НШ-3970.2014.9) и молодого доктора наук (МД-1929.2013.2), а также грантов РФФИ 13-07-97008 и 14-07-31092.