Равновесие водяного газа с углеродом

Автор: Кузнецов Юрий Серафимович, Качурина Ольга Ивановна

Журнал: Вестник Южно-Уральского государственного университета. Серия: Металлургия @vestnik-susu-metallurgy

Рубрика: Физическая химия и физика металлургических систем

Статья в выпуске: 4 т.15, 2015 года.

Бесплатный доступ

Рассчитанные возможные параметры равновесия водяного газа с углеродом представлены поверхностью пространственной диаграммы в координатах x CO- x H2 - T, которую можно дополнить графиком проекций изотермических сечений поверхности на плоскость составов x CO- x H2. Рассмотрены различные способы получения газовой атмосферы, кислородный потенциал которой позволяет восстанавливать оксиды металлов. Наиболее технологически простым способом получения восстановительной по отношению к оксиду металла газовой смеси является нагревание водяного пара в контакте с углеродом. В этом случае состав получающегося водяного газа определяется только температурой нагрева. Максимальная концентрация водорода достигает x H2 ≈ 0,5 при нагревании H 2O - C до ~ 900 К, а при нагревании до температур выше 1100 К получается смесь газов-восстановителей с равными концентрациями x CO = x H2 = 0,5. При нагревании в контакте с углеродом смесей H 2O - CO 2 получается водяной газ, в котором уменьшается концентрация H 2 и увеличивается концентрация CO. Газовую атмосферу (Н 2 - Н 2О - СО - СО 2) любого состава можно получить нагреванием в контакте с углеродом смесей (Н 2 - СО). Образование CO 2 происходит в результате реакции диссоциации CO, а паров воды - в результате реакции Н 2 + СО 2 = Н 2О + СО. Предложена методика количественной оценки газификации углерода парами воды Н 2О и диоксидом СО2. Расчетами показано, что в зависимости от состава исходной газовой смеси и температуры реакции газификации C + CO 2 = 2CO и C + H 2O = CO + H 2 могут протекать в прямом и обратном направлениях.

Еще

Водяной газ, углерод, параметры равновесия, условия получения, кислородный потенциал

Короткий адрес: https://sciup.org/147156974

IDR: 147156974 | DOI: 10.14529/met150404

Текст научной статьи Равновесие водяного газа с углеродом

Водяной газ (Н 2 – Н 2 О–СО–СО 2 ) является основой газовых атмосфер в металлургических технологиях. Особенности равновесия реакции водяного газа в приближении линейной зависимости стандартного изменения энергии Гиббса реакции от температуры обсуждались в работе [1]. Параметры водяного газа изменяются, если он находится в равновесии с углеродом. В этом случае задача по оценке параметров равновесного состояния решается расчетом равновесий любых двух независимых реакций из трех возможных в системе ( A r G T , Дж):

H2 +CO2 =H2O+CO,

ArGT (1) = 36 580 - 33,465 T;(1)

C+CO2 = 2CO,

ArGT (2) = 172140 -177,7 T;(2)

C+H2O=CО+H2,

ArGT (3) = 135 560 -144,235 T.(3)

Появление второй фазы при неизменном числе компонентов приводит к изменению вариантности системы:

с = к + 2 – ф = 3 + 2 – 2 = 3.

Если заданы и не изменяются давление и температура, число степеней свободы с = к – ф = 3 – 2 = 1.

Следовательно, равновесные характеристики сис- темы Н2–Н2О –СО–СО2–С можно определить, лишь задав какой-либо один равновесный параметр. Возможны несколько вариантов решения задачи.

Рассмотрим для примера вариант расчета совместных равновесий реакций (1) и (2). Здесь следует отметить следующее обстоятельство. В «простой» двухкомпонентной двухфазной системе C–CO₂–CO при постоянной температуре и заданном давлении 1 атм строго фиксируется не только соотношение x CO / x _C O₂ = K ₂, но и концентрации и отношение концентраций x _CO x _CO (табл. 1).

Приведенная в последней строке табл. 1 информация позволяет определить температуру восстановления оксидов металлов в системе СО–СО₂–С. Условие восстановления оксида определяется неравенством ( lg p о ) < ( lg p о ) На—

² СО – СО₂– С ² MeО

пример, для оксида Fe3O4 это неравенство выполняется при температуре выше 917 К, а для оксида FeO – выше 955 К [2].

В системе Н2–Н2О–СО–СО2 –С фиксируют-xCO xH O ся соотношения K 1 =-----—, K2 = xCO2 xH2

xCO xH также соотношение K3 =------ = —2. Однако xH2O

Таблица 1

Концентрации компонентов и окислительный потенциал равновесной с углеродом газовой смеси (СО 2 – СО) при 1 атм

Т , К	700	800	900	1000	1100	1200	1300	1400	1500
K 2 , атм	2,73-Ю^-4	0,0110	0,1956	1,952	12,82	61,53	232	724	1940
x CO	0,0164	0,0995	0,3552	0,7283	0,9322	0,9843	0,9957	0,9986	0,9995
x CO ₂	0,9836	0,9005	0,6448	0,2717	0,0678	0,0157	0,0043	0,0014	0,0005
–lg p _O ₂	29,48	25,85	23,14	21,24	19,97	19,05	18,30	17,65	17,14

отношение концентраций x _CO x _CO , как это следует из правила фаз, изменяется. Следовательно, изменяется и отношение x _H x _{H O} – в соответствии с равновесием реакции водяного газа (1). С одной стороны, это означает, что для расчета параметров равновесной системы необходимо кроме температуры и давления задавать еще какой-либо параметр, например, концентрацию любого компонента равновесного водяного газа. С другой стороны, это означает, что состав водяного газа может быть любым, но в некотором зависящем от температуры интервале. Покажем это конкретными расчетами.

При заданных температуре Т и давлении P решаем систему трех уравнений с четырьмя неизвестными:

СО 2 монотонно увеличиваются, а концентрации Н 2 с ростом x _CO уменьшаются, тогда как изменение x _{H O} характеризуются максимумом. Во-вторых,

x CO x H₂O

K1 - xCO2 xH2

A G (1)

e RT

2 A G (2)

K ₂ - x^COP - e RT x CO₂

x i ^- x CO

+ ^x H₂O + ^x CO₂

+ ^x H₂ ^- 1.

Если задавать концентрацию, например, x _CO рав-

новесной газовой смеси, то решение уравнений (4) будет таким:

xC2O xCO2 - K2 ;

системы

x H 2 O

¹ ^- ^x CO ^- ^x CO₂ ,

1 x CO + 1 K 1 x CO₂

задаваемая молярная доля x _CO не может быть больше некоторого значения, определяемого равновесием реакции газификации углерода (см. табл. 1). Расчеты при задаваемых x _CO , превышающих приведенные в табл. 1 величины, дают не имеющие физического смысла (отрицательные) концентрации Н₂О и Н₂.

Возможные параметры равновесия систем Н₂–Н₂О–СО–СО₂–С можно представить пространственной диаграммой в координатах x _CO – x _H – T (рис. 1). На рис. 1 показаны возможные концентрации Н₂ и СО в равновесной системе Н 2 –Н 2 О–СО–СО 2 –С при температурах в интервале 800…1000 К, причем точки, характеризующие возможные сочетания x _CO , x _H при разных температурах, располагаются на криволинейной поверхности MLFE . Линия FE на плоскости x _CO – T определяет максимальные концентрации СО в равновесном водяном газе (см. табл. 1). На изотерме LF точками показаны некоторые результаты расчетов, которые в табл. 2 выделены жирным курсивом. Пространственную диаграмму можно дополнить графиком, показывающим проекции изотермических сечений поверхности MLFE на плоскость составов x _CO – x _H (рис. 2). Изотермы соединяют точку с координатами x _CO = 0, x _H = 1

x H₂

1 - xCO -

x _C ² _O

1 +

K 1 x CO

Замечание. Такие же расчетные уравнения получаются, если оценивать совместные равновесия других двух независимых реакций (1) и (3).

Для примера в табл. 2 для трех температур и давления 1 атм представлены результаты расчетов по соотношениям (5) возможных концентраций компонентов водяного газа, равновесного с углеродом. Следует отметить два обстоятельства. Во-первых, возможные равновесные концентрации

с точками, координаты которых определяют состав равновесного газа в двухкомпонентной двухфазной системе СО–СО 2 –С, линия EF на рис. 1. Изотермические линии являются образующими криволинейной поверхности MLFE , любая точка которой определяет возможные концентрации Н₂ и СО в равновесном с углеродом водяном газе.

Внешне проекции изотерм на рис. 2 похожи на прямые линии. Однако эти линии, строго говоря, нельзя считать прямыми. Действительно, уравнение

¹ - ^x CO -

² x CO

x H 2

K 2

1 + ^K 1 ^x CO

K 2

(5*)

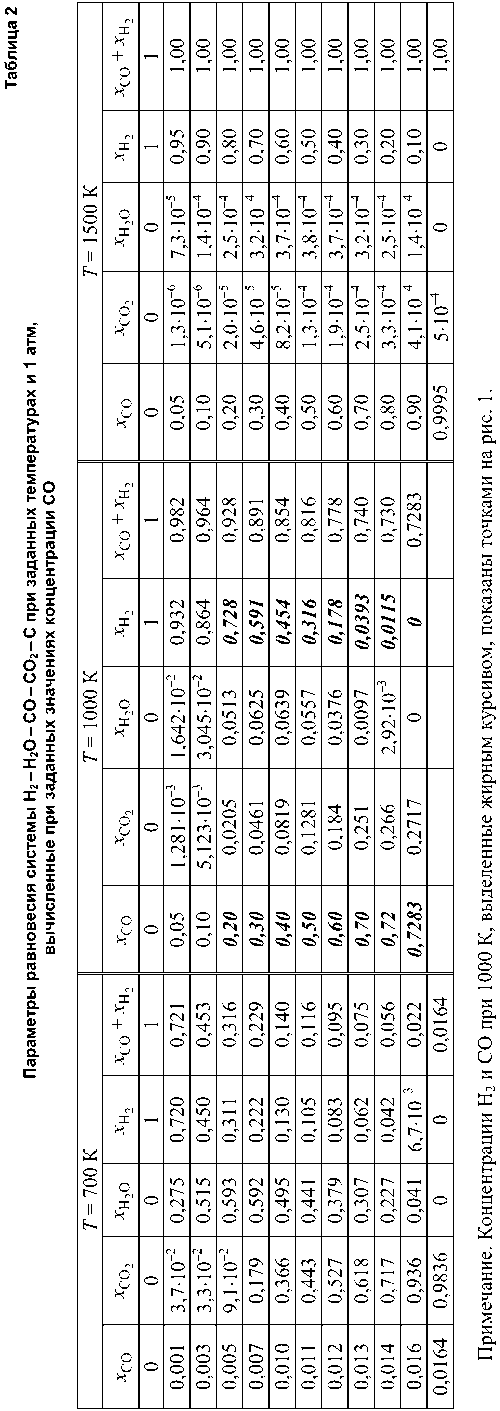
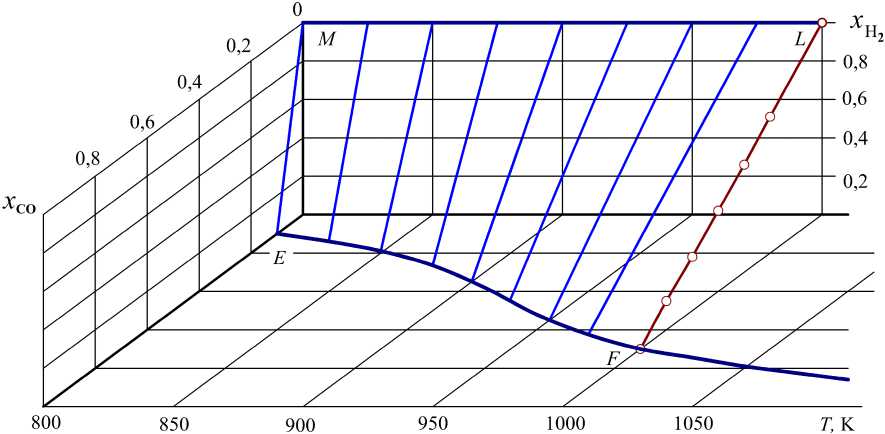
Рис. 1. Параметры равновесия водяного газа с углеродом: точки на изотерме 1000 К – вычисленные концентрации Н 2 и СО (табл. 2)

Рис. 2. Концентрации газов Н 2 и СО в системах Н 2 –Н 2 О–СО–СО 2 –С: линия 1 – 800; 2 – 850; 3 – 900; 6 – 1000; 7 – 1100; 8 – выше 1300 К; 4 – 917;

5 – 955 К. Точки – концентрации x _CO и x _H для 1000 К приведены в табл. 2

определяет нелинейные соотношения между x _COи x _H . Аппроксимация этих зависимостей линейными функциями характеризуются такими коэффициентами корреляции при разных температурах:

1500 К – R ² = 1; 1100 К – R ² = 1;

1000 К – R ² = 1, 950 К – R ² = 1;

923 К – R ² = 0,999; 900 К – R ² = 0,997;

850 К – R ² = 0,977; 800 К – R ² = 0,902;

700 К – R ² = 0,304.

Можно с достаточной достоверностью соотношения между x _H и x _CO при температурах выше 850 К считать линейными и определять такими уравнениями:

xCO _ * xCO 1 - x H2 1; 1 - x H2 = xCO; (6) xCO 1 x H2 = 1 - xCO, xCO где xCO - концентрации CO, определяющие равновесия системы C–CO–CO2. Как видно из рис. 2 и табл. 2 при температурах выше 1100 К суммарная концентрация восстановителей (xCO + xH ) в водяном газе, равновесном с графитом, близка к единице.

Представленными расчетами показано, что равновесие водяного газа с углеродом может реализоваться при бесконечном множестве сочетаний концентраций его компонентов. В практических технологиях процессы восстановления оксидов металлов чаще всего осуществляются в многокомпонентных газовых смесях в присутствии углерода. В зависимости от исходных параметров реальной технологии можно получать газовые атмосферы строго контролируемого состава. Приведем здесь расчеты составов водяного газа в равновесных состояниях «H 2 ( a моль) – H 2 O ( b моль) – CO ( c моль) – CO 2 ( d моль) – C», получающихся такими различными способами:

1) при нагревании до заданной температуры паров воды в контакте с углеродом – нагревание исходной системы

«H₂O ( b ₀ моль) – C»;

2) при нагревании исходной системы

«H 2 O ( b 0 моль) – CO 2 ( d 0 моль) – C»;

3) при нагревании исходной системы

«H 2 ( a 0 моль) – CO ( c 0 моль) – C».

Способ 1. Нагревание исходной системы

«H₂O ( b ₀ моль) – C»

Этот способ представляет, по нашему мнению, наибольший практический интерес, так как в промышленных технологиях создать атмосферу водяного газа технически проще и с наименьшими затратами можно в результате нагревания паров воды в контакте с углеродом. Рассчитаем параметры перехода исходной системы «Н 2 О ( b 0 моль) – С» в равновесие «Н 2 ( a ) – Н 2 О ( b ) – СО ( c ) – СО 2 ( d моль) – С», используя термодинамические характеристики двух независимых реакций газификации углерода (2) и (3). При изотермической выдержке исходной системы «Н₂О ( b ₀ моль) – C» образуются в результате протекания реакции (3) газы H₂ и CO, газ CO₂образуется по реакции водяного газа (1), что провоцирует реакцию (2). Представим исходное и равновесное состояния системы:

C + CO 2 = 2CO C + H 2 O = CO + H 2

Исходное – – b – – состояние 0

Равновесное d c b c a состояние

Равновесные количества газов определяем решением системы уравнений с учетом баланса по во дороду b0 = b + a и кислороду b0= b + 2d + c:

(асЛ ( с² ^

K = ac ; K = c- ; 2 = a + b + c + d . (7)

3 I b 2 I ² I d 2 I

Так как уравнений три, а неизвестных четыре, то возможно, например, такое решение, когда величины c, b и d выражаются через a:

c =---- aJC 1 -----; ь = - a ; d = a— c . (8)

2(b0 - a) + aK 1 0

Тогда, варьируя задаваемую величину a, опреде- ляем такое её значение, при котором вычисленные величины c, b и d и концентрации:

a bcd xh2 =2; xh2o =2; xco = 2; xco2 = 2

удовлетворяют трем константам равновесия K ₁, K ₂и K ₃. Результаты расчетов представлены в табл. 3. Например, из приведенных в табл. 3 результатов расчетов для 1000 К получаем для изменений энергии Гиббса реакций:

² x CO

—

x((,

I ^CO 2 J

A r G T (2) = A _rG T (2) + RT In

= 172 140 - 177,7 - 1000 + 8314 - ln⁰------ = 0;

0,0683

[ x x ^H ]

I x H 2 O J

A _rG_T (3) = A r G T (3) + RT ln

= 135 560-144235 + 8314 - In

0,3652 ■ 0,5019

0,0646

≈0;

[ x H ^ O x CO ]

I x H₂ x CO 2 J

A _rG_T (1) = A r G T (1) + RT ln

= 36 580 - 33 465+ 8314 - In

0,0646 ■ 0,3652

0,5019 ■ 0,0683

≈ 0.

Равенство нулю изменений энергии Гиббса реакций свидетельствует о равновесии всех трех возможных в системе реакций.

Из результатов термодинамических расчетов следует, что составы газовой смеси, получающейся при любой изотермической выдержке разных количеств паров воды (b0) в контакте с углеродом, представляется одной политермической линией, соединяющей точку N с координатами xНзо = 1 и точку М с координатами xH2 = xCO = 0,5 (рис. 3). Для каждой температуры получается одно единственное равновесное состояние, не зависящее от количества воды. Протекание реакций газификации приводит к заметному увеличению количества газов в системе. Из сравнения величин lgpO для получающейся газовой фазы и, например, для оксида железа FeO следует, что восстановление FeO до Fe в газовой смеси, полученной нагреванием Н2О–С, возможно при температурах выше ~ 900 К.

Образование водяного газа при нагревании паров воды в контакте с углеродом является следствием протекания двух реакций газификации. При изотермической выдержке исходной системы образуются в результате протекания реакции (3) газы H2 и CO, диоксид углерода CO2 может образоваться по двум реакциям:

CO + H 2 O = CO 2 + H 2 и 2CO = CO 2 + C.

Apriori следует ожидать, что углерод расходуется по реакции (3) и образуется сажистый углерод в результате диссоциации CO. Можно определить вклад

Таблица 3

Параметры равновесной системы «Н 2 ( a ) –Н 2 О ( b ) – СО( c ) –СО 2 ( d моль) – С», получающейся при нагревании исходной системы «Н 2 О (1 моль) – С», 1 атм

T , К	700	850	900 (0,5)	900 (1)	900 (2)	1000	1100	1300	1500
a	0,3059	0,6265	0,36325	0,7265	1,4530	0,8860	0,9641	0,9959	0,9992
b	0,6941	0,3735	0,1368	0,2735	0,5470	0,1140	0,0359	0,0041	0,0008
c	0,0069	0,1313	0,1304	0,2608	0,5216	0,6447	0,8988	0,9916	0,9987
d	0,1495	0,2476	0,1164	0,2328	0,4657	0,1207	0,0326	0,0022	0,0003
∑	1,1564	1,3789	0,7468	1,4937	2,9873	1,7653	1,9315	1,9937	1,9989
x H 2	0,2645	0,4543	0,4864	0,4864	0,4864	0,5019	0,4991	0,4994	0,4999
x H ₂ O	0,6003	0,2709	0,1831	0,1831	0,1831	0,0646	0,0186	0,0021	0,0004
x CO	0,0059	0,0953	0,1746	0,1746	0,1746	0,3652	0,4653	0,4974	0,4996
x CO ₂	0,1293	0,1795	0,1559	0,1559	0,1559	0,0683	0,0170	0,0011	0,0001
x _H ₂ + x _CO	0,2705	0,5496	0,6610	0,6610	0,6610	0,8671	0,9645	0,9969	0,9995
x _H2 / x CO	44,50	4,7698	2,7856	2,7856	2,7856	1,3743	1,0726	1,0043	1,0005
lg p _O ₂	–30,36	–25,04	–23,76	–23,76	–23,76	–21,84	–20,57	–18,89	–17,68
(lg p _O ₂ ) _FeO	—	–25,52		–23,74		–20,72	–18,24	–14,42	–11,63

Примечания: Для 900 К расчет выполнен при заданных величинах b ₀ = 2; 1 и 0,5 моль.

Кислородные потенциалы для системы FeO–Fe–O2 определены по данным, приведенным в работе [2].

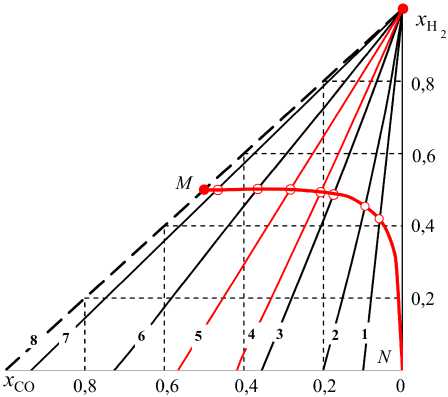
Рис. 3. Параметры равновесия (линия NM ) систем H 2 –H 2 O–CO–CO 2 –C, получающихся после нагревания смеси H 2 O–C: T = 800 (1), 850 (2), 900 (3), 917 (4), 955 (5), 1000 (6), 1100 (7), 1700 К (8)

каждой из реакций (2) и (3) в общий расход углерода при нагревании исходной системы Н2О–С:

C + CO 2 = 2CO C + H 2 O = CO + H 2

Исходное – состояние

Равновесное d состояние

Равновесное s состояние

– b0 – – c b c a y –2s b0– y y –2s y

Здесь в первой строке после уравнений реакций показано количество паров воды в исходном состоя- нии. Во второй строке – количества газов в системе после нагревания паров воды в контакте с углеродом до какой-либо температуры. В третьей строке – то же самое с учетом вклада каждой из реакций газификации в образовании равновесной газовой фазы:

y – количество углерода, вступившего в реакцию (3);

s – количество углерода, образовавшегося по реакции

2CO = CO 2 + C. (2^*) Тогда константы равновесия реакций при P = 1 атм и условие нормировки:

У ( У - 2 5 )

3"(b0 - У )2 ;

К _ ( У - 2 5 )².

K 2 = v ;

5 2

2 = a + b + c + d = b0 + y - 5.

Решение этой системы уравнений приводит к таким расчетным формулам:

_t У ⁽ b o ^- У ) .

⁵ K

Л y + 2 (bo - y) (10)

K ₃

a = y ; b = b o - y ; d = 5 ; c = y - 2 5 .

Результаты расчетов приведены в табл. 4. Равновесные параметры газовой фазы, приведенные в этой таблице, абсолютно совпадают с параметрами, полученными расчетами по уравнениям без детализации расхода углерода. Кроме того, из результатов расчетов следует, что с повышением температуры увеличивается до единицы ( b 0 = 1 моль) количество углерода, вступившего в реакцию газификации (3). Получающийся по этой реакции оксид CO разлагается с образованием CO₂ и сажистого углерода и это снижает общий расход углерода на газификацию. С повышением температуры уменьшается до нуля количество получающегося сажистого углерода, по реакции разложения монооксида CO:

при T ^ ~ 1700 К, y = n C (3) ^ 1, 5 = n C (2 * ) ^ 0, У n C = y - 5 ^ 1, У ^ 2 моль.

Для любого другого исходного количества паров воды b ₀ моль:

при T ^ ~ 1700 К, y = n C (3) ^ b ₀, 5 = n C (2 * ) ^ 0, У n C = y - 5 ^ b 0 , У ^ 2 b 0 .

Таким образом, с повышением температуры все возрастающую роль в газификации углерода играют пары воды и при температурах выше ~ 1100 К получается практически бинарная газовая смесь (CO–H2) с равными концентрациями компонентов.

Способ 2. Нагревание исходной системы

«H₂O ( b ₀ моль) – CO₂ ( d ₀ моль) – C»

В исходной системе соотношения количеств Н2O и СО2 могут быть любыми. Возможен расчет равновесия при 1 атм с детализацией расхода углерода по реакциям (2) и (3):

	C + CO 2 = 2CO		C + H 2 O = CO + H 2
Исходное		–
состояние	0		0
Равновесное	d ₀ + s		b 0 – y y –2 s y
состояние	d ₀ + s	y –2 s	b 0 – y y –2 s y

Решение системы трех уравнений с четырьмя неизвестными:

_ y ⁽ y ^- ² ⁵ )
³ = ( b 0 - У ) 2 ;

K = (y - 25 )2

² ( d 0 + 5 ) 2 ;

Ss = b0 + d 0 + y - 5

дает следующие соотношения для расчетов:

У| b0 - У -
V

5 = "K

-2 y + ² ( ^b 0 ^- y )

K ₃

a = y ; b = b ₀ - y ; d = d ₀ + 5 ; c = y - 2 5 ,

Таблица 4

Параметры равновесия систем Н 2 –Н 2 О–СО–СО 2 –С, получающихся при нагревании исходной системы «Н 2 О (1 моль) – С», давление 1 атм

T, К 700 850 900 917 955 1000 1100 1300 1500 y = nC (3) 0,3059 0,6265 0,7265 0,7582 0,8231 0,8860 0,9640 0,9960 0,9993 s =nC (2) 0,1495 0,2476 0,2328 0,2199 0,1789 0,1207 0,0327 0,0021 0,00023 ∑nC = y – s 0,1564 0,3789 0,4937 0,5383 0,6442 0,7653 0,9313 0,9939 0,9990 a, моль 0,3059 0,6265 0,7265 0,7582 0,8231 0,8860 0,9640 0,9960 0,9993 b, моль 0,6941 0,3735 0,2735 0,2418 0,1769 0,1140 0,0360 0,0040 0,0007 c, моль 0,0069 0,1313 0,2608 0,3184 0,4652 0,6447 0,8986 0,9918 0,9988 d, моль 0,1495 0,2476 0,2328 0,2199 0,1789 0,1207 0,0327 0,0021 0,00023 ∑, моль 1,1564 1,1389 1,4937 1,5383 1,6442 1,7653 1,9313 1,9939 1,9991 V, л 66,38 96,11 110,23 115,7 128,8 144,8 174,2 212,6 245,9 xH2 0,2645 0,4543 0,4864 0,4929 0,5007 0,5019 0,4991 0,4994 0,4999 xH2O 0,6003 0,2709 0,1831 0,1573 0,1076 0,0646 0,0186 0,0021 0,0004 xCO 0,0059 0,0953 0,1746 0,2069 0,2829 0,3652 0,4653 0,4974 0,4996 xCO2 0,1293 0,1795 0,1559 0,1429 0,1088 0,0683 0,0170 0,0011 0,0001 lg pO2 –30,36 –25,04 –23,76 –23,37 –22,60 –21,84 –20,57 –18,89 –17,68 (lg pO2 )Fe3O4 – –25,52 –23,43 –22,74 – –19,84 –15,43 –12,21 –8,69 (lg pO2 )FeO – –25,52 –23,74 – –22,0 –20,72 –18,24 –14,42 –11,63 которые при d0 = 0 превращаются в уравнения (10) для системы H2O–C.

Для примера результаты расчетов по уравнениям (11) для одной температуры 900 К приведены в табл. 5 и на рис. 4. Как и прежде параметры равновесного состояния определяются точками пересечения правых фрагментов полученных кривых N1, N2, N3 и др. с изотермой 6, определяющей возможные концентрации СО и Н2 в равновесной системе «водяной газ – углерод». Левые фрагменты 1M1, 2M2, 3M3 и др. реализуются при нагрева- ниях «Н2O (b0) – СО2 (d0) – С» до температур выше 900 К. При некотором увеличении общего количества газа соотношение xC2O xCO фиксировано, а отношение концентраций xCO ! xCO изменяется. С увеличением отношения d0 / b0 точка пересечения перемещается по изотерме 6 вниз, то есть в равновесной газовой смеси молярная доля водорода xH снижается от 0,4864 при d0 = 0 (отсутствие в исходной смеси СО2) до нуля в отсутствии в исходной смеси паров воды, b0 = 0.

Таблица 5

Параметры равновесия систем Н 2 –Н 2 О–СО–СО 2 –С, получающихся при нагревании до 900 К исходной системы «Н 2 О (1 моль) – СО 2 ( d 0 ) – С», 1 атм

b 0	1	1	1	1	1	1	1	0
d 0	0	0,5	0,845	1	2	3	9	9
y = n C (3)	0,7265	0,6635	0,6427	0,6360	0,6108	0,5990	0,5789	0
s = n C (2)	0,2328	0,0875	0	–0,0368	–0,2678	–0,4907	–1,7982	–1,9432
∑ n C = y – s	0,4937	0,5760	0,6427	0,6728	0,8786	1,0897	2,3771	1,9432
a , моль	0,7265	0,6635	0,6427	0,6360	0,6108	0,5990	0,5789	0
b , моль	0,2735	0,3365	0,3573	0,3640	0,3892	0,4010	0,4211	0
c , моль	0,2608	0,4884	0,6414	0,7096	1,1463	1,5804	4,1754	3,8865
d , моль	0,2328	0,5875	0,8456	0,9632	1,7322	2,5093	7,2018	7,0668
∑, моль	1,4937	2,0759	2,4870	2,6728	3,8786	5,0897	12,3772	10,9533
V , л	110,23	153,2	183,54	197,3	286.2	375,6	913,4	808,4
x H 2	0,4864	0,3196	0,2584	0,2379	0,1575	0,1177	0,0468	0
x H ₂ O	0,1831	0,1621	0,1437	0,1362	0,1003	0,0788	0,0340	0
x CO	0,1746	0,2352	0,2579	0,2655	0,2956	0,3105	0,3373	0,3551
x CO ₂	0,1559	0,2830	0,3400	0,3604	0,4466	0,4930	0,5819	0,6449
lg p _O ₂	–23,76	–23,50	–23,42	–23,40	–23,30	–23,32	–23,19	–23,14

Для определения параметров состояния, по- СО могут быть любыми, а состав исходной смеси лучающегося при нагревании исходной системы (Н₂ –СО) представляется точками на диагонали «СО 2 ( d 0 ) –С», рассчитывается равновесие реак- «( x _CO = 1) – ( x _H = 1)». Образование диоксида уг- ции (2): лерода CO₂ при изотермической выдержке смеси ^{C + CO} ² ^{= 2CO} (Н 2 –СО) происходит в результате реакции диссо- ^{Исходное состояние} ^d ⁰ ^– циации 2CO = C + CO 2 , а паров воды – в результа- Равновесное состояние d* = d. _ ^c c* те Реакции водяного газа Н + СО 2 = Н 2 О + СО. ^По - ⁰ 2 этому рассчитываем равновесия тех же реакций: _c * C + CO 2 = 2CO C + H 2 O = CO + H 2 S, = d * + c * = d _n + —; Исходное * 0 2 - c o - c o ao ² состояние ^{0 0 0} „ ( c * ) Равновесное _ _ Ki = ----------; (12) s c ₀-2 s - y y c ₀-2 s - y a ₀- y ² 2 состояние ^{0 0 0} д 2 ⁽ c ) d о 4 Решение системы трех уравнений с четырьмя не известными: c * = 2 d ₀J— K— . _ ( ^а 0 ^_ y )( ^c 0 ^_ ² s ^_ y ) 04 4 + K₂ ^K 3 = _v ; ² y S Для примера в последнем столбце табл. 5 приве- ₂ дены результаты расчета для 900 К и d 0 = 9 моль. ( ^c 0 ^_ ² s ^_ y ) Таким образом, нагреванием смеси (Н 2 О-СО 2 ) ² = s s ^; разного состава в контакте с углеродом можно получит водяной газ, концентрация водорода в ко- ^S * = a ⁰ ⁺ ^c ⁰ ^- s ^- ^y тором меньше величин, определяемых линией NM . дает такие расчетные уравнения: Например, нагреванием до 900 К можно получить y ( c ₀ - y ) водяной газ, в котором концентрации компонен- s = к _а Г к ) ’ тов изменяются в пределах: x _H - от 0,4864 до 0; „ ⁺ ^y 1 ² „ 1 ² K 3 1 ^к 3 ) x H ₂ O - от 0,1831 до 0; x _CO-от 0,1746 до 0,3551; ( a^ _ y ) y x CO - от 0,1831 до 0,6449. x H² = S ; x H²O =S ; Способ 3. Нагревание исходной системы x = ⁽ ^c 0 ^_ ² s ^_ y ) . x = s «H₂ ( а ₀ моль) - CO ( c ₀ моль) - C» ^CO S ’CO ^ Этим способом можно получить атмосферу Результаты расчетов по этим уравнениям приведе- водяного газа любого состава. Количества Н₂ и ны в табл. 6 и на рис. 5. Таблица 6 Параметры перехода исходной системы «H 2 ( a ₀ моль) – CO ( c ₀ моль) – C» в равновесия при изотермической выдержке 900 К ( K 2 = 0,1956; K 3 = 0,4638), 1 атм
a 0	3	1,8571	1	1	1	1	1	1	0
c 0	1	1	1	1,1665	2	3	7	19	19
( x H ₂ ) исх	0,75	0,65	0,50	0,4616	0,333	0,25	0,125	0,05	0
y = n C (3)	0,4624	0,3823	0,2735	0,2890	0,3366	0,3640	0,4010	0,4210	0
s = n C (2)	0,1246	0,1703	0,2328	0,2889	0,5876	0,9632	2,5094	7,2014	7,4488
∑ n C = y – s	0,3378	0,2120	0,0407	0	–0,2510	–0,5992	–2,1084	–6,7804	–7,4488
a	2,5376	1,4748	0,7265	0,7110	0,6634	0,6360	0,5989	0,5790	0
b	0,4624	0,3823	0,2735	0,2890	0,3366	0,3640	0,4010	0,4210	0
c	0,2884	0,2772	0,2608	0,2997	0,4883	0,7096	1,5802	4,1762	4,1024
d	0,1246	0,1703	0,2328	0,2889	0,5876	0,9632	2,5094	7,2014	7,4488
∑	3,4129	2,3046	1,4936	1,5886	2,0759	2,6728	5,0895	12,3776	11,5512
V	251,88	170,07	110,23	117,24	153,20	197,25	375,61	913,41	852,5
x _H ₂	0,7435	0,6400	0,4864	0,4475	0,3196	0,2380	0,1177	0,0468	0
x H ₂ O	0,1355	0,1659	0,1831	0,1819	0,1621	0,1362	0,0788	0,0340	0
x CO	0,0845	0,1202	0,1746	0,1887	0,2352	0,2655	0,3105	0,3373	0,3551
x CO ₂	0,0365	0,0739	0,1559	0,1819	0,2830	0,3603	0,4930	0,5819	0,6449
lg p _O ₂	–24,39	–24,08	–23,76	–23,69	–23,50	–23,40	–23,26	–23,19	–23,14

Таблица 7

Параметры перехода исходной системы «H 2 ( a ₀ моль) – CO ( c ₀ моль) – C» в равновесия при изотермических выдержках, 1 атм

a 0	a ₀ = 1, c ₀ = 1, ( x _H ₂ ) _исх = 0,5				a ₀ = 1, c ₀ = 3, ( x _H ₂ ) _исх = 0,25
T , К	850	900	950	1000	850	900	950	1000
y = n C (3)	0,3735	0,2735	0,1849	0,1140	0,4830	0,3640	0,2539	0,1614
s = n C (2)	0,2476	0,2328	0,1851	0,1207	1,0763	0,9632	0,7622	0,5094
∑ n C = y – s	0,1259	0,0407	–0,0002	–0,0067	–0,5933	–0,5992	–0,5083	–0,3480
a	0,6265	0,7265	0,8151	0,8860	0,5170	0,6360	0,7461	0,8386
b	0,3735	0,2735	0,1849	0,1140	0,4830	0,3640	0,2539	0,1614
c	0,1313	0,2608	0,4449	0,6447	0,3644	0,7096	1,2216	1,8198
d	0,2476	0,2328	0,1851	0,1207	1,0763	0,9632	0,7622	0,5094
∑	1,3789	1,4936	1,6300	1,7654	2,4407	2,6728	2,9838	3,3292
V	96,11	110,23	126,98	144,76	170,12	197,25	232,44	272,99
x H 2	0,4543	0,4864	0,5001	0,5019	0,2118	0,2380	0,2500	0,2519
x H ₂ O	0,2709	0,1831	0,1134	0,0646	0,1979	0,1362	0,0851	0,0485
x CO	0,0953	0,1746	0,2730	0,3651	0,1493	0,2655	0,4094	0,5465
x CO ₂	0,1795	0,1559	0,1135	0,0684	0,4410	0,3603	0,2555	0,1531
lg p _O ₂	–25,04	–23,76	–22,70	–21,84	–24,65	–23,40	–22,34	–21,49
(lg p _O ₂ ) _Fe ₃ _O ₄	–25,52	–23,43	—	–19,84	–25,52	–23,43	—	–19,84
(lg p _O ₂ ) _FeO	–25,52	–23,74	–22,15	–20,72	–25,52	–23,74	–22,15	–20,72

«H 2 (1 моль) – CO (1 моль) – C» и «H 2 (1 моль) – CO (3 моль) – C» до разных температур. С повышением температуры мало изменяется концентрация водорода и заметно повышается концентрация CO. При этом примерно на три порядка увеличивается равновесное давление кислорода, однако восстановительные способности получающейся газовой фазы по отношению к монооксиду железа при ~ 900 и ~ 920 К, соответственно, сохраняются.

Выводы

1. Нагреванием паров воды Н 2 О, смесей (Н₂О–СО₂) и (Н₂–СО) в контакте с углеродом можно получить газовую смесь (Н 2 –Н 2 О–СО–СО 2 ), в которой возможно восстановление оксидов металлов. Самым эффективным, технологически простым и дешевым способом получения нужной газовой смеси является нагревание паров воды в контакте с углеродом, (Н₂О – С).
2. Предложена методика термодинамических расчетов составов газовой смеси и расхода углерода на процессы газификации. Эта методика может быть полезной для термодинамических расчетов процессов восстановления оксидов металлов, введенных в рассмотренные системы.
3. Полученные данные позволяют обоснованно оценить роли окислительной газификации углерода диоксидом СО₂ и парами Н₂О. Авторы работы [3], по нашему мнению, некорректно судят о несоответствии кинетических особенностей газификации углерода термодинамическим предпосылкам. Причина этого состоит в том, что авторы определяют термодинамическую возможность газификации величинами стандартных изменений энергии Гиббса реакций (2) и (3), то есть по суще-

ству константами равновесия, и не учитывают исходные состояния. Результаты термодинамических расчетов для 900 К (см. табл. 5) показывают, что расход углерода по двум реакциям газификации существенно зависит от соотношения исходных количеств Н₂О и СО₂. Например, при молярном соотношении Н 2 О и СО 2 1 : 0,845 = ~ 1,183 углерод газифицируется только парами воды:

y = n C (3) = 0,6427; s = n C (2) = 0 моль.

Если молярное соотношение Н₂О и СО₂ в исходной смеси больше 1,183, расход углерода по реакции (3) y = n _C(3) незначительно увеличивается до 0,7265 моль в отсутствии СО 2 . При этом увеличивается выделение сажистого углерода по реакции 2CO = C + CO 2 . Если же молярное соотношение Н₂О и СО₂ меньше 1,183, y = n _C(3) незначительно уменьшается, тогда как существенно увеличивается количество углерода, вступившего в реакцию газификации (2).

Список литературы Равновесие водяного газа с углеродом

Кузнецов, Ю.С. Термодинамический анализ реакции водяного газа/Ю.С. Кузнецов, Г.Г. Михайлов, О.И. Качурина. -Вестник ЮУрГУ. Серия «Металлургия». -2014. -Т. 14, № 1. -С. 5-11.
Михайлов, Г.Г. Анализ фазовых равновесий в системе «оксиды железа -углерод -СО -СО2»/Г.Г. Михайлов, Ю.С. Кузнецов, О.И. Качурина, А.С. Чернуха. -Вестник ЮУрГУ. Серия «Металлургия». -2013. -Т. 13, № 1. -С. 6-13.
Гришин, А.М. О несоответствии кинетических закономерностей термодинамическим предпосылкам реакций газификации углерода Н2О и СО2/А.М. Гришин, В.К. Симонов, И.С. Щеглова. -Изв. вузов. Черная металлургия. -2013. -№ 7. -С. 64-67.

Статья научная