Равновесная плоская трещина с угловыми точками контура в упругом слое
Автор: Соболь Борис Владимирович, Рашидова Елена Викторовна, Борисова Екатерина Викторовна, Петренкова Софья Борисовна
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 5 (66) т.12, 2012 года.
Бесплатный доступ
Рассмотрена трёхмерная статическая задача теории упругости о равновесии упругого слоя, ослабленного плоской прямоугольной трещиной. Трещина расположена в срединной плоскости слоя, поддерживается в раскрытом состоянии под действием нормальной нагрузки, приложенной к её берегам. Грани слоя находятся в условиях гладкого контакта с двумя жёсткими основаниями. Применением двумерного интегрального преобразования Фурье к уравнениям равновесия задача сведена к решению известного сингулярного интегро-дифференциального уравнения относительно функции раскрытия трещины. Решение уравнения строится прямым вариационным методом. В окрестности угловых точек контура решение достраивается численно, с учётом заранее выделенной особенности. Получены значения коэффициента интенсивности нормальных напряжений в окрестности контура трещины. Установлены особенности поведения решения в окрестности прямолинейных участков и угловых точек контура.
Трещина, контур, коэффициент интенсивности напряжений, слой, сингулярное интегральное уравнение, вариационный метод, силовой критерий разрушения, угловая точка, окрестность, относительная толщина слоя
Короткий адрес: https://sciup.org/14249882
IDR: 14249882 | УДК: 539.375
Текст научной статьи Равновесная плоская трещина с угловыми точками контура в упругом слое
Введение. Как было установлено в многочисленных работах отечественных и зарубежных исследователей (например, [1]), в точках гладкости контура трещины функция раскрытия трещины должна иметь асимптотику
у(х,у) = N(x,y^n1R (х,у),
где п^х, у) — расстояние по нормали от внутренней точки области до контура трещины, N(x, у) — некоторая регулярная функция.
В случаях, когда контур трещины имеет особые точки: во-первых, нарушается состояние плоской деформации в окрестности этих точек, во-вторых, меняется показатель особенности поля напряжений и перемещений в окрестности контура вблизи таких точек. Определению показателей при особенности в зависимости от угла излома контура посвящён ряд работ отечественных и зарубежных исследователей [2].
Если в плоскости расположения трещины ввести полярную систему координат с полюсом в особой точке контура, то функция раскрытия трещины в окрестности этой точки асимптотически может быть, описана соотношением
у(х,у) = 1(о) £
где р, о — полярные координаты точки, До) — некоторая регулярная функция.
Рассмотрим наиболее распространённый частный случай, когда контур трещины в точке излома образует прямой угол. В этом случае установлен следующий показатель особенности в соотношении (2): s = 0,816.
Постановка задачи. Продемонстрируем методику решения задач теории упругости для трещин с особыми точками контура на примере задачи о прямоугольной трещине в слое.
Трещина расположена в срединной плоскости слоя, поддерживается в раскрытом состоянии под действием нормальной нагрузки, приложенной к её берегам. Грани слоя находятся в условиях гладкого контакта с двумя жёсткими основаниями. Применением двумерного интегрального преобразования Фурье к уравнениям равновесия в перемещениях задача о продольной равновесной трещине в слое сводится к решению двумерного сингулярного интегро-дифференциального уравнения [3]:
д Ц Y (^ п) ® + JJ Y (5, П) S (х,у Л п) ^ = -^ Р^х, у), (3)
здесь (х, у) е Q, Q — область расположения трещины в плане, R = ^х - ^)2 + (у - п)2 / д2 д2
9 = Е / Г2(1 - v)1, Д = —5- + —5-, р(х, у) — нагрузка, приложенная к берегам трещины, Е— модуль
Юнга, v — коэффициент Пуассона, 5(х,уД,п) — регулярная часть ядра уравнения, характе ризующая влияние геометрических параметров задачи: размеров трещин в плане, относительных расстояний между ними и (или) до границ рассматриваемых тел. Для задачи о трещине, лежащей в срединной плоскости слоя, имеем [3]:
5(х,У Д,П) = ^F(R / h), F (f) = [t/ [H (u) - цр0 (ut)du,
" о
H(u) = u(sh2u +2u)(chu - Y) 1, J0(x) — функция Бесселя 1-го рода.
Решение уравнения (3) будем строить прямым вариационным методом, описанным в [4]. В рассматриваемом случае область интегрирования описывается неравенствами: О:|х|<а, |у|<Д
(рис. 1)
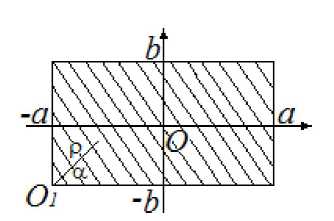
Рис. 1. Схема трещины
Метод решения. Выберем, систему координатных функций таким образом, чтобы установленная выше асимптотика (2) с соответствующим показателем явно учитывалась. Ограничимся рассмотрением, как наиболее характерного частного случая, равномерно распределённой нагрузки р(х,у) на берегах трещины, где р(х,у) = р = const . Решение задачи при этом строится в виде:
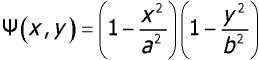
г ' ? ini/?/ \л тпх ппу...
\(х,у) = -аЧ)щ (x,y^^Amn cos —- cos —(4) у m=0 л=0 3и
Коэффициенты Amn в разложении (4) определяются из условия минимума функционала:
3 (y) = [JY (*,У) JJY (5,П)К2 (5 - X,п - у) cE,dc\dxdy - JJ Y (Л У) pdxdy,(5)
Q QУ Q где К2 (а, Р) = [ j л/t/2 +и2£ (b^u7 +и2) cos а u cos 0 vdudv. 0 0'
Следует отметить, что в аналогичном виде вариационный метод был использован при исследовании задачи о равновесии упругого пространства ослабленного трещиной [5]. В качестве координатных функций в этой работе были использованы степенные функции с множителем, явно содержащим требуемую асимптотику в окрестности контура трещины.
Минимизация функционала (5) в рассматриваемом случае приводит к следующей системе линейных алгебраических уравнений для определения коэффициентов Атп:
М N
=2^(пт,пл),
/=о ;=о где т = 0,1,2,...,М; /7 = 0,l,2,...,/V.
В данной задаче f (а,Р) = ^^-^. При вычислении коэффициентов системы (6) ис-v ар пользовано значение интеграла
[ [ Ф1/2 (х, у) cos — cos dxdy = — abf (а, р), полученного с помощью (3.752) из [6].
Вычисление элементов четырёхмерной матрицы Q9mn производится с использованием представлений (5.4) из [4].
Сравнительный анализ и сопоставление численных результатов. Конечной целью исследования задачи теории упругости для тела с трещиной, как известно, является определение критических нагрузок, при которых трещина становится неустойчивой и начинает расти. Поскольку в качестве основного критерия разрушения в данной работе принят силовой критерий [7], перейдём к определению коэффициента интенсивности нормальных напряжений в окрестности контура трещины в каждом из рассмотренных случаев. Особое внимание в дальнейшем также будет уделяться сравнительному анализу применяемых здесь методов и сопоставлению численных результатов.
Контроль точности решения задачи вариационным методом приводился сопоставлением результатов при различном количестве используемых координатных функций (Ми /V). В частности, вычислялась амплитуда раскрытия берегов трещины в центре при различных соотношениях геометрических параметров задачи. Во всех рассмотренных ниже случаях расхождение результатов счёта при М = N = 4 и М = N = 6 не превысило 3,5 %.
Кроме того, о достоверности получаемых результатов могут свидетельствовать и следующие качественные рассуждения. При вытягивании трещины вдоль одной из осей симметрии, амплитуда её раскрытия в центре, а также численные значения коэффициента интенсивности нормальных напряжений в средней части большей из сторон прямоугольного контура должны быть близки к известным соответствующим решениям задач о полосовой трещине и эллиптической трещине с такими же полуосями. Причём, поскольку упомянутая полосовая трещина ширины 2Ь содержит внутри себя прямоугольную область, а эллиптическая, в свою очередь, содержится в последней, решение задачи о прямоугольной трещине, по известному принципу сравнения [8], должно быть заключено между соответствующими решениями этих двух задач. В таблице 1 представлены приведённые значения амплитуды вертикальных перемещений у (0,0)0 /(ра) в центре трещины для полосовой [3], эллиптической [9] и прямоугольной трещины. Вычисления проведены для предельного случая Л оо. Для сопоставления, здесь же приведён соответствующий результат работы [5].
В случаях эллиптической и прямоугольной трещин при вычислениях принято следующее соотношение размеров Ь!а = 0,5. Вычисления показывают, что и при конечной толщине слоя установленные закономерности не нарушаются.
Таблица 1
Приведённые значения амплитуды вертикальных перемещений в центре полосовой, прямоугольной и эллиптической трещины
|
(4) |
[5] |
|
0,882 |
0,872 |
|
[9] |
[3] |
|
0,826 |
1,000 |
Перейдём к анализу численных значений коэффициента интенсивности нормальных напряжений К, при обходе по контуру прямоугольной трещины. В этой задаче более удобно рассматривать не относительные значения параметра К, (как в задачах об эллиптических трещинах, где точное аналитическое решение для предельного случая Л оо существует), а абсолютные. Вдоль каждой из сторон прямоугольной области значения коэффициента интенсивности нормальных напряжений будем вычислять по формулам:
м n mn Y
Kia^ = pa -/(х, 0)Ц Amn cos — ,(7)
V U т=0 п=0d
R /V /?п 1 /
^(y) = psJ-/(0,y)^^4ncos-2-.(8)
Y d т=0 п=0v
Графики изменения коэффициента интенсивности нормальных напряжений вдоль большей и меньшей сторон прямоугольника представлены на рис. 2 (а, б). Вычисления проведены для ряда значений параметра K = h ] а при b / а = 0,5. Отметим, что максимальные амплитудные значения К, достигает на большей стороне. Опираясь на силовой критерий разрушения, можно сделать вывод, что при достижении приложенной нагрузки своего критического значения, рост прямоугольной трещины начнётся с середин больших сторон. На рис. 3 представлены соответствующие графики, иллюстрирующие решение задачи для случая трещины квадратной формы (Ь = а).
С приближением к угловым точкам контура трещины коэффициент интенсивности нормальных напряжений стремится к нулю. Это обусловлено особым видом асимптотики (2) функции раскрытия трещины в окрестности этих точек, с соответствующим показателем. Перейдём к построению решения задачи у(х, у) в окрестности угловых точек.
Вдоль лучей, выходящих из угловой точки контура под различными углами а, вычисляются значения функции: £(а) = у(х,у)/(р/а).
Фрагменты результатов таких вычислений представлены в таблице 2 (при b/а = 0,5) и таблице 3 (при b/а = 1).
В каждом из случаев, представленных в таблицах, нетрудно обнаружить интервал изменения отношения р/ае[грг2], в котором функция с достаточно высокой точностью сохраняет стабильность вдоль каждого луча и изменяется лишь при переходе с одного луча на другой. Упомянутая закономерность ранее была установлена для предельного случая рассматриваемой здесь задачи, соответствующего Л^оо [5], [10].
Расположение и размеры этой зоны зависят от а, отношения сторон области трещины b/а и относительной толщины слоя К Таким образом, определив для каждого значения величину £(о) на указанном отрезке [гг, г-Д, представляется возможным достроить искомую функцию ^х, у) по асимптотической формуле (2) непосредственно до вершины угла трещины.
Графики функции L(a) при различных относительных толщинах слоя представлены на ри сунке 4 (слева — b/а = 0,5, справа — b/а = 1).
Следует отметить симметричность функции ^х, у) в окрестности угловой точки контура относительно биссектрисы. Между тем, сама прямоугольная область расположения трещины такой симметрией не обладает.
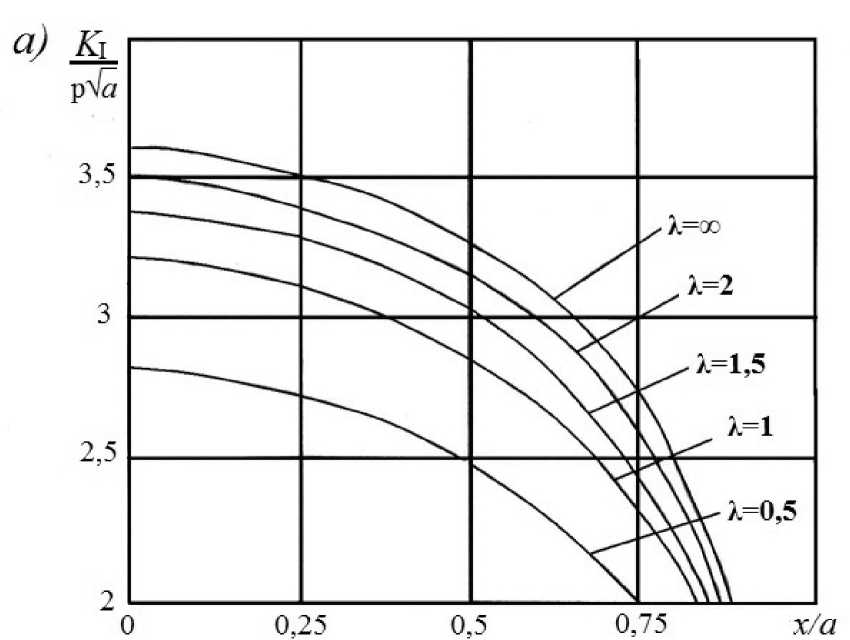
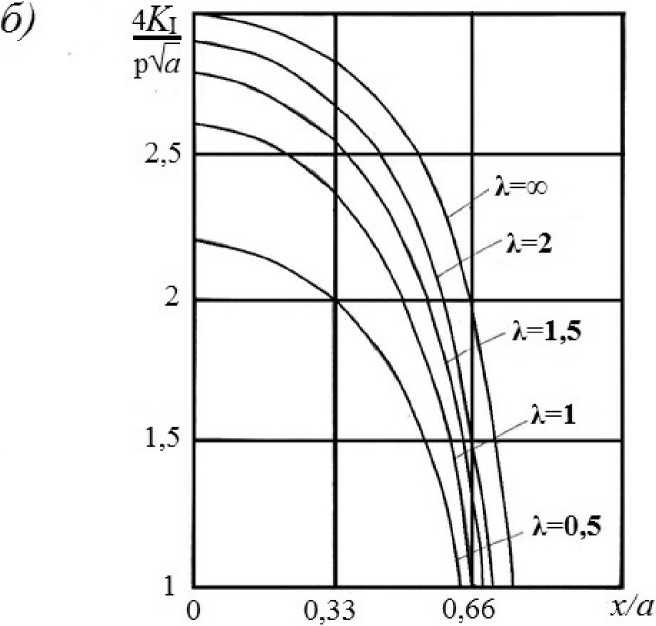
Рис. 2. Изменение коэффициента интенсивности нормальных напряжений вдоль большей (а) и меньшей (б) сторон прямоугольной трещины
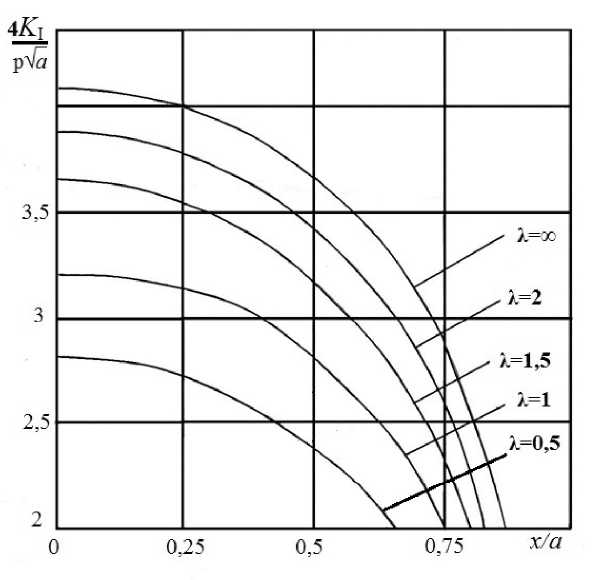
Рис. 3. Изменение коэффициента интенсивности нормальных напряжений для случая трещины квадратной формы (Ь = а)
Таблица 2
Приведённые значения функции раскрытия вдоль лучей, выходящих из угловой точки прямоугольной трещины ^bja = 0,5)
|
1 |
X |
2 |
||||
|
о = п/4 |
о = п/8 |
о = Зп/8 |
Pla |
о = п/4 |
о = п/8 |
о = Зп/8 |
|
2,38 |
2,04 |
2,01 |
1/16 |
2,60 |
2,24 |
2,21 |
|
2,59 |
2, 21 |
2,18 |
1/8 |
2,84 |
2,48 |
2,39 |
|
2,67 |
2,29 |
2,22 |
3/16 |
2,92 |
2,52 |
2,43 |
|
2,66 |
2,30 |
2,20 |
1/4 |
2,92 |
2,53 |
2,41 |
|
2,60 |
2,29 |
2,14 |
5/16 |
2,36 |
2,53 |
2,36 |
|
2,55 |
2,24 |
2,07 |
3/8 |
2,80 |
2,48 |
2,28 |
|
2,42 |
2,18 |
1,99 |
7/16 |
2,67 |
2,41 |
2,19 |
|
2,31 |
2,07 |
1,90 |
1/2 |
2,57 |
2,33 |
2,10 |
Таблица 3
Приведённые значения функции раскрытия вдоль лучей, выходящих из угловой точки квадратной трещины (d/а = 1)
|
1 |
X |
2 |
||
|
а = п/4 |
а = п/8 |
Pla |
а = п/4 |
а = п/8 |
|
1,91 |
2,27 |
1/16 |
2,28 |
2,70 |
|
2,00 |
2,51 |
1/8 |
2,51 |
3,00 |
|
2,20 |
2,61 |
3/16 |
2,63 |
3,13 |
|
2,24 |
2,64 |
1/4 |
2,69 |
3,18 |
|
2,25 |
2,64 |
5/16 |
2,71 |
3,19 |
|
2,23 |
2/63 |
3/8 |
2,73 |
3,19 |
|
2,19 |
2,58 |
7/16 |
2,67 |
3,15 |
|
2,14 |
2,51 |
1/2 |
2,63 |
3,09 |
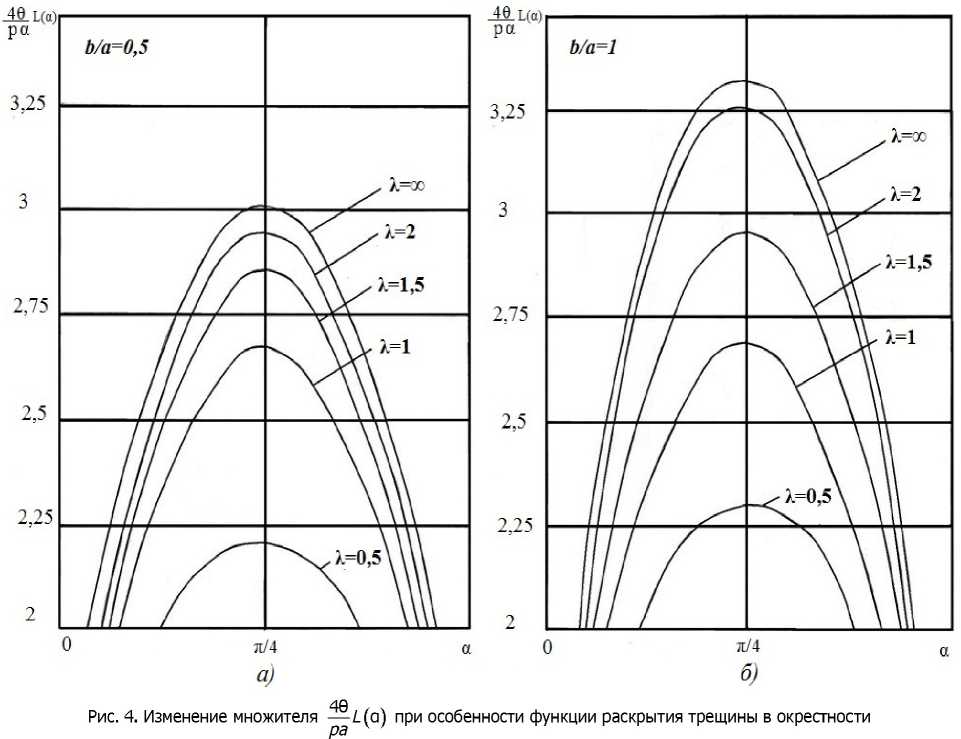
угловой точки для прямоугольной (а) и квадратной (б) формы трещины
Выводы
-
1. В результате проведения численного эксперимента установлено, что решение задачи о прямоугольной трещине в упругом слое удовлетворяет принципу сравнения.
-
2. Коэффициент интенсивности напряжений достигает своего максимального значения при обходе по контуру в окрестности центра длинной стороны прямоугольной области.
-
3. Установлена симметричность функции раскрытия трещины в окрестности угловой точки контура, независимо от соотношения размеров прямоугольной области.
Список литературы Равновесная плоская трещина с угловыми точками контура в упругом слое
- Sneddon, I. N. The stress intensity factor for a flat elliptical crack in an elastic solid under uniform tension/I. N. Sneddon//Int. J. Eng. Sci. -1979. -V. 17. -№ 2. -p. 92-103.
- Bazant, Z. Tree-dimentional harmonic functions near termination or interaction of gradient singularity lines: A general numerical method/Z. Bazant//Int. J. Eng. Sci. -1974. -№ 12. -p. 221-243.
- Александров, В. М. Тонкие концентраторы напряжений в упругих телах/В. М. Александров, Б. И. Сметанин, Б. В. Соболь. -Москва: «Физматлит», 1993. -224 c.
- Сметанин, Б. И. Равновесие упругого слоя, ослабленного системой плоских трещин/Б. И. Сметанин, Б. В. Соболь//ПММ. -1984. -Т. 48. -№. 6. -С. 1030-1038.
- Гольдштейн, Р. В. Качественные методы в механике сплошных сред/Р. В. Гольдштейн, В. М. Енотов. -Москва: Наука, 1989. -С. 110-115.
- Градштейн, И. С. Таблицы интегралов, сумм, рядов и произведений/И. С. Градштейн, И. М. Рыжик. -Москва: Наука, 1971. -1108 с.
- Irvin, G. R. Analysis of stress and strain near the end of a crack, traversing a plate/G. R. Irvin//J. Appl. Mech. -1957. -№ 3. -P. 361-364.
- Гольдштейн, Р. В. Вариационные оценки для коэффициента интенсивности напряжений на контуре плоской трещины нормального разрыва/Р. В. Гольдштейн, В. М. Енотов//Изв. АН СССР, МТТ. -№ 3. -С. 59-64.
- Пэрис, П. Анализ напряжённого состояния около трещин/П. Пэрис, Дж. Си//Прикладные вопросы вязкости разрушения. -Москва: Мир. -1968. -С. 64-142.
- Мураками, Ю. Справочник по коэффициентам интенсивности напряжений. (в 2-х томах)/Ю. Мураками. -Москва: Мир. -1990. -Т. 1 -448 с. -Т. 2 -1014 с.


