Равновесное состояние прямолинейной внутренней трещины вблизи угловой точки упругой области, подкрепленной по контуру

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2025PNRPU MECHANICS BULLETIN

В современном производстве широко применяется технология нанесения на изделия тонкого гибкого покрывающего слоя, который препятствует негативному воздействию окружающей среды, а также за счет своих высоких механических характеристик позволяет усилить прочность всего изделия. Кроме того, усиление изделий покрытиями препятствует разрушительным воздействиям внутренних дефектов самого изделия.

Наиболее важными с позиции обеспечения прочности являются области концентрации напряжений, в частности, клиновидные области. Изучению плоских задач теории упругости о трещинах в клиновидных областях посвящены публикации как зарубежных, так и отечественных ученых. В частности, в работе [1] рассмотрены задачи о трещине конечной длины, выходящей на вершину клина, а также – полубесконечной внутренней трещине, расположенной на биссектрисе.

Цикл публикаций Б.И. Сметанина [2; 3] посвящен задачам о расклинивании, а также о внутренних трещинах в клине при различных условиях на его гранях.

Значительное количество работ посвящено изучению концентрации напряжений в упругих телах для областей с угловыми точками контура. В работе [4] приведено решение задачи для конуса и клина, в кото- ром использован метод разделения переменных. Выделены, исследованы и решены пять частных задач. Работы Д.А. Пожарского [5; 6] посвящены исследованию пространственных задач теории упругости для клиновидного тела. Рассмотрены случаи эллиптической в плане трещины и полосового разреза. На внешних гранях клина ставятся условия скользящей или жесткой заделки, или отсутствия напряжений.

В работах [7; 8] представлены подходы к нахождению асимптотического решения вблизи угловых точек, исследованы особенности найденных упругих решений. Публикации [9; 10] посвящены исследованию пространственных задач теории упругости о полосовой трещине в составном упругом клине и о периодической цепочке эллиптических трещин, расположенных параллельно ребру клина.

В монографии В.М. Александрова, С.М. Мхитаряна [11] произведен асимптотический анализ точного решения задачи для упругой полосы при условии ее малой относительной толщины, высокой податливости в отношении изгибных деформаций. Эти результаты позволяют, в частности, сформулировать специальные граничные условия, моделирующие влияние тонких гибких покрытий

Исследования [12; 13] изучают и анализируют поведение напряжений в вершинах внутренних трещин с учетом поверхностных эффектов. Для случая плоских и антиплоских задач подбором необходимых характеристик найдены условия для устранения сингулярности напряжений. В исследовании [14], посвященном изучению анизотропной клинообразной области, построено решение задачи, зависящее от геометрических параметров клина и механических характеристик материала, определен показатель сингулярности напряжений. В статье [15] представлено общее решение для определения порядка сингулярности напряжений в анизотропном клине. Порядок зависит от угла раствора клина, граничных условий и свойств материала. Чтобы уменьшить степень сингулярности напряжений в углу клина, можно определить направление волокна, соответствующее минимальному порядку сингулярности.

Отметим, что, наряду с задачами о трещинах, задачи о включениях и контактные задачи рассматриваются как задачи со смешанными граничными условиями и являются идентичными по применяемым подходам и методам.

В публикациях [16–18] исследован цикл пространственных задач о составном упругом клине. Рассмотрены различные варианты смешанных граничных условий на смежных гранях клиновидных слоев (трещина, включение). Исследованы случаи, когда внешние грани клина свободны от напряжений, находятся в условиях гладкого контакта или зафиксированы жестко. Решение проведено асимптотическим методом с использованием интегральных преобразований. Построены интегральные уравнения. Определено НДС в окрестности границ смены граничных условий. В монографии [19] представлены теоретические основы решения задач статики упругого клина, приведены фундаментальные решения уравнений теории упругости для клиновидной области, исследованы особенности напряженно-деформированного состояния в ее вершине. В работах [20, 21] рассмотрены задачи о пространственной упругой клиновидной области для случая смешанных граничных условий на ее гранях и с учетом сил трения. Одна из граней области контактирует с цепочкой жестких штампов. Представлены интегральные уравнения, решение которых проведено численно. Получены значения вдавливающих сил для различных значений угла раскрытия клиновидной области.

В работе [22] рассмотрена задача о полубесконеч-ной антиплоской интерфейсной трещине, расположенной между двумя функционально-градиентными клиновидными областями. Изучено влияние упругих свойств составляющих на интенсивность напряжений в вершинах трещины и показатель сингулярности в вершине самой структуры. Публикация [23] посвящена решению задачи об антиплоской трещине, выходящей из вершины составного функционально-градиентного клина. Исследовано влияние соотношений геометрических и физических параметров задачи на коэффициент интенсивности напряжений в вершине трещины.

Как известно, контактные задачи механики деформируемого твердого тела, как и задачи теории трещин, относятся задачам со смешанными граничными условиями и по применяемым подходам и методам являются родственными. В связи с этим приведем одну из недавних публикаций В.А. Бабешко [24], в которой построено точное решение статической контактной задачи о действии с трением жесткого клиновидного штампа, занимающего первый квадрант, на слой изотропного композитного материала.

Постановка задачи. Переход к сингулярному интегральному уравнению

Рассмотрим плоскую задачу об изотропной упругой клиновидной области, стороны которой усилены тонким гибким материалом. В полярной системе координат ( r , ϕ ) рассматриваемая область определяется неравенствами: r ≥ 0 , ϕ ≤α , где величина 2 α определяет угол раскрытия клина.

Внутри области, на ее биссектрисе, находится трещина в виде внутреннего разреза длиной l = b - a , где ϕ = 0 , a ≤ r ≤ b– место расположения трещины. Действие нормальных сил p ( r ) на стороны трещины приводит к ее раскрытию. Предполагаем, что на бесконечности при r →∞ компоненты тензора напряжений и вектора перемещений стремятся к нулю. В работе будет исследовано НДС тела на концах трещины.

Публикации [25 ; 26] посвящены решению обратной задачи в аналогичной постановке, в них проведен процесс идентификации дефектов изотропных упругих тел, в том числе клиновидной области с покрытием [26], на основе ультразвуковых колебаний и сверточных нейронных сетей. Решение прямой задачи, излагаемое в предлагаемой работе, дополняет и обеспечивает комплексный подход к исследованию, а именно полученные в данной работе результаты позволяют определить критическое состояние рассматриваемого объекта.

Исследуемая в работе область представлена на рис. 1.

Симметрия тела относительно луча ϕ = 0 позволяет свести задачу к исследованию половины области: r ≥ 0 , 0 <ф<а .

Обозначим функции раскрытия трещины

γ ( r ) = v ( r , ϕ ) _{ϕ=- 0} - v ( r , ϕ ) _{ϕ=+ 0}

ϑ ( r ) = ^{∂ u} ∂ϕ

ϕ=- 0

∂ u

∂ϕ

ϕ=+ 0

где u ( r , ϕ ) и v ( r , ϕ ) – компоненты вектора перемещений: радиальная u и тангенциальная v .

Искомое решение удовлетворяет уравнениям равновесия в перемещениях, заданным в полярной системе координат:

Lu +

1 d0 2 ----vV = 0.

1 - 2 ц Э r r^{2 m}

T 1 d0 2

Lv +-- 7—+—7 u m = 0,

(1 - 2 ц ) r dm r 2

где ц - коэффициент Пуассона; L = —++    -+

Э r² r d r r²

. 1 d21

+“ VT; 0 = ur+ -(u + vm )■ r dm

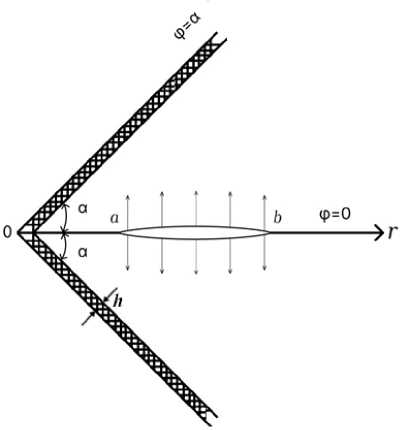
Рис. 1. Плоская клиновидная область со сторонами, усиленными тонким гибким материалом, содержащая конечный разрыв (трещину) на биссектрисе

Fig. 1. A flat wedge-shaped area with sides reinforced with thin flexible material, containing a finite crack on the bisectrix

Компоненты тензора напряжений в полярной системе координат:

( 1 a v 1

О = 2 G I + u + ^m ^ r dm r

ц

1 - 2 ц

I              ( 1 3 u 3 v 1 |

⁰ I , t= 2 G I--+--- v I ,

J ^m ^ r Зф 3 r r J

где G - модуль сдвига.

На берегах трещины и ее продолжении выполняются условия:

для m = 0 : °m = -P (r) при a ^ r < b , v = 0 при 0 < r < a и r > b .(3)

Условия на гранях области:

rrm= 0, r > 0;(4)

m = a: ^m= 0, 4 G1 hu"r = (1 -ц^т rm- 2ц1 h<,(5)

где G 1 - модуль сдвига покрытия; ц 1 - коэффициент Пуассона покрытия; h – толщина покрытия. Предполагаем, что относительная толщина покрытия мала по сравнению с длиной трещины: h / ( b - a ) <<  1.

Для формулировки граничного условия (5) использовано асимптотическое представление решения задачи для упругой полосы в предположении ее малой относительной толщины и отсутствии сопротивления на изгиб [11]. Исследование условия (5) для различных соотношений толщины и жесткости покрытия проведено в работе [27].

Применяя преобразование Меллина к (1), получаем систему обыкновенных дифференциальных уравнений (ОДУ) 2-го порядка:

(1 + к )( s ² - 1) U - (1 - k ) U ; - 2( s + k X = 0,

(1 - k )( s ² - 1) V - (1 + K X + 2( s - k ) U m = 0,     (6)

где к = 3 - 4 ц .

Общее решение (6) имеет вид:

U = ( s + к ) [ c 1 sn ⁺ + c ₂ cs ⁺ ] + ( s - 1) [ c ₃ sn ^- + c ₄ cs ^- ] , (7)

V = - ( s - к ) [ c 1 cs ⁺ - c ₂ sn ⁺ ] - ( s - 1) [ c ₃ cs ^- - c ₄ sn ^- ] , (8)

где c i - произвольные постоянные , i = 1, 2, 3, 4;

sn+ = sin [(s + 1)m], sn- = sin [(s - 1)m], cs+ = cos [(s + 1)m], cs- = cos [(s - 1)m] ■

8+i м am=— J 4 s(s - 1)r~s-1 ds,             (9)

i П

8- i ^M

G ⁸⁺ i ”

^T r m =— f A T ^sr - ^{s -1 ds} ,                ⁽¹⁰⁾

i n8- где

A _a = c 1 sn ⁺ + c ₂ cs ⁺ + c ₃ sn ^- + c ₄ cs ^- ,

A = ( s + 1) [ c 1 cs ⁺ - c ₂ sn ⁺ ] + ( s - 1) [ c ₃ cs ^- - c ₄ sn ^- ] ■

Учитывая (9), (10) в соотношениях (4), (5), получаем систему линейных алгебраических уравнений для определения коэффициентов c i ( i = 1, 2, 3, 4).

c1 (1 + s) - c 3 (1 - s) = 0, c1( s-к) - c3(1 - s) = Y*, c1 sn <+ + c 2 cs a + c3 sn a + c4 cs a = 0,

2 G 1 h ( s + 1) r ^{- 1} ( ( s + k ) [ c 1 sn a + c ₂ cs a ] +        (11)

^{+ ( s -} 1) [ ^c 3 ^sn a ^{+ c} 4 ^cs a ] ) =

= G ( (1 -ц 1 ) - 2 ц 1 h ( s - 1) ) x

^X ( ^{( s +} 1) [ ^c 1 ^cs a ^{- c} 2 ^sn a ] ^{+ ( s -} 1) [ ^c 3 ^cs a ^- c 4 ^sn a ] ) ■

Здесь sn a = sin [(s + 1)a], sn a = sin [(s - 1)a], cs a = cos [(s + 1)a], cs a = cos [(s - 1)a],

σ+ i ∞

γ ( r ) =         γ *( s ) r ^{- s}ds ,

2 π i _{σ- i ∞}

∞

Y * ( s ) = j Y ( r ) r s - 1 dr .

Re ( K ( u , r ) ) = — 8 GG₁ hr (1 + u ²)(1 -ц )(1 -^ ₁)sin² a sh² u a/ ( 16 G 1 ² h ²(1 -μ )²(cos2 α+ ch 2 u α )² -

- ( 4 G ₁ hu (1 -μ )(cos2 α+ ch 2 u α ) + Gr (1 -μ ₁)( u sin2 α+ sh 2 u α ) ) ² ) .

Решение системы (11) имеет вид:

Im ( K ( u , r ) ) = ( 8 G ₁ ² h ² (1 — ^ ) 2 (cos2 a + ch 2 ua )( u sin 2 a — sh 2 u a ) —

Здесь

^c 2 ⁼

* γ c1 = 1+κ,

- 2 G (1 -μ 1 ) γ ^* r

^c 3 ⁼

1 +κ γ ^*(1 + s ) (1 +κ )(1 - s ) ^,

_{c =} 2 G (1 -μ 1 ) γ ^*(1 + s ) r

⁴       (1 +κ )(1 - s )

^A 4 ^.

- ( Gr ( μ ₁ - 1)( sh ² u α- u ²sin² α ) - 2 G ₁ hu (1 -μ )( u sin2 α- sh 2 u α ) )

( 4 G ₁ hu (1 -μ )(cos2 α+ ch 2 u α ) + Gr (1 -μ ₁)( u sin2 α+ sh 2 u α ) ) )

( ( 4 G ₁ h (1 -μ )(cos2 α+ ch 2 u α ) ) ² -

- ( 4 G ₁ h (1 -μ )(cos2 α+ ch 2 u α ) u + Gr (1 -μ ₁)( u sin2 α+ sh 2 u α ) ) ² ) .

Далее умножаем

Получаем

Nm ₂ Dm

Nm ₂ Dm

Dm = Gr (1 -μ ₁)( s sin2 α+ sin2 s α ) + 8 G ₁ h (1 + s )(1 -μ ) cs _α ⁺ cs _α ^- ,

Nm ₂ = ( s sin² α+ sin² s α ) + 4 G ₁ h (1 + s )(1 -μ ) sn _α ⁺ cs _α ^- ,

Nm ₄ = ( s sin² α- sin² s α ) + 4 G ₁ h (1 + s )(1 -μ ) sn _α ^- cs _α ⁺ .

Подставим найденное выражение σ_ϕ (9) с уже определенными коэффициентами (13) в условие сопряжения (3), получаем для a ≤ r ≤ b :

δ+ i ∞

γ ^* K ( s , r ) sr ^{- s - 1} ds =- p ( r ),       (14)

iπ(1-μ) δ-i∞ где

+ Im ( K ( u , r

Учитывая четность Re ( K ( u , r ) ) и нечетность Im ( ft ( u , r ) ) по переменной u , имеем в (21) нечетную функцию в действительной части выражения, которая при интегрировании по симметричному промежутку приводит к нулевому значению.

Замена (17), приведенные выше рассуждения и четность мнимой части выражения (21) сводят (16) к интегральному уравнению

—^f— f Y( P ) d рГ ( Re( к ( u , r ) ) sin I u in ^p+ п (1 + K ) a p 0'             'I r )

I T^/      \ I 1 P I I J

+ Im I K ( u , r )cos I u in— I I udu = — rp ( r ).

I I r ))

K ( s , r ) =

Gr (1 -μ ₁)( s ²sin² α- sin² s α ) + 2 G ₁ h (1 + s )(1 -μ )( s sin2 α- sin2 s α )

Gr (1 -μ ₁)( s sin2 α+ sin2 s α ) + 8 G ₁ h (1 + s )(1 - μ ) cs _α ⁺ cs _α ^-

Подставим (12) в (14):

4G bγ(ρ)   δ+i∞ dρK(s,r)sds=-rp(r).(16)

iπ(1+κ)αρ    δ-i∞

Проведем интегрирование

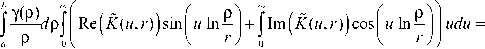
= j Re ( K ( u , r ) ) u j ^Y ( ^P ) sin I u in ^P1 d p du +

0                 a ^p V r ⁾

Выполним замену:

s = iu ,

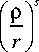
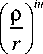
I p Ip I = cos I u In — I + i Sin I u In — I .

+

r

r

j Im ( K ( u , r ) ) u j 0 a

γ ( ρ ) ^ρ

cos

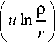
d ρ du .

После проведенной замены функция K ( s , r ) переходит в функцию K ( u , r ).

Интегрируем по частям

K i ( u , r ) = -

Gr (1 -μ ₁)( sh ² u α- u ²sin² α ) + 2 iG ₁ h (1 + iu )(1 -μ )( u sin2 α- sh 2 ua ) 4 G ₁ h (1 + iu )(1 -μ )(cos2 α+ ch 2 u α ) + iGr (1 -μ ₁)( u sin2 α+ sh 2 ua ) ^.

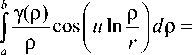
γ ( ρ ) = u

1    11 p I J

—cos I u in— I = dv p    V r )

Представим ft ( u, r ) = Re ( ft ( u, r ) ) + i Im ( Kt ( u, r ) )

1 bb I

= — f Y ( p )sin I u in u b V

[ Жш f u In P1 d p = a p i r )

γ(ρ) =u i -fi p 'a a

— sin I u ln — I = dv

P I r J

Получаем

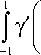
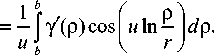
f i+z n7f z-x^    f i+z v a exp I — II11      I a exp I — | dZ = nk     f 1 + x } f     f 1 + x

= —0" a exP I "k" I P I a exP I "k"

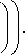
Подставляем выражения (23), (24) в интегральное уравнение (22), получаем

8 G f Y’ ( p ) d p f ^f Re ( Ki ( u , r ) ) cos ^f u ln ^{p n (1 + k )} b 0 I                I r

- Im ( Ki ( u, r ) ) sin I u In ^p II du = - r p ( r ).

Проведенный анализ функций   Re( K ( u , r )) и

Im( K ( u , r )) при u →∞ показал, что

Re ( Ki ( u , r ) ) = O ( e ’2 ^{u a} ),

Im ( Ki ( u , r ) ) = - 1 + O ( e ^{2u a} ), 0 .     (26)

L ( u , r ) = Re ( Ki ( u , r ) ) cos ^ u In — J -

( Im ( K ( u , r ) ) + 1 ) sin I u In —I + sin I u In —I ,

Вводим замену

-

Ф ⁽ Z ⁾ = Y‘I a exp I I I exp

I I k ))

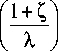
Уравнение (28) принимает вид

1 fZ Z- x nk   f 1 + x ^ f     f 1 + x

I фО! .   I d Z = —exp | т I p I ^a exp I т 11 , ⁽³¹⁾

- 1 I k )       0 I k ) I I k ))

где x ≤ 1 .

Преобразуем выражение (28) для функции l(r), учитывая значение интеграла, ∞ sin(ut)du = 1 [28].

0 ^t

∞

∞

∞∞∞ ₁

l ( r ) = f M ( u , r ) du + f sin( ut ) du = f M ( u , r ) du + -. (32) 000 ^t

Получаем сингулярное интегральное уравнение задачи:

M ( u , r ) = Re ( Ki ( u , r ) ) cos I u In ^p

-

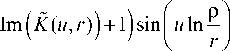
f Ф ( Z )

- 1

k      fl /I            f 1 + x 11 J

+ M u , α exp        du

.Z- x 0 I 4 k ))

=- π^λ q ( x ), x ≤ 1, θ

Тогда L ( u , r ) = M ( u , r ) + sin I u In ^p I и уравнение

I r J

(25) принимает вид:

, . f 1 + x ^ f f 1 + x q ⁽ x ) = exp I — I p I ^a exp I —

d ζ =

b∞ f Y‘(p) dpf L(u,r) du = “rP(r),         (27)

a 0                    ^θ

G здесь θ=

1 -μ

Пусть

∞

l ( r ) = f L ( u , r ) du                   (28)

Переходим к безразмерным переменным, используя замену переменных

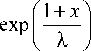
ρ= a exp

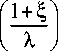
Z = 2 ^f In b |

I a J

Обе части уравнения (33) разделим на λ≠ 0 .

Таким образом, получаем сингулярное интегральное уравнение (СИУ) с ядром Коши:

f Ф ( Z ) .. ¹ + ¹ f M I u , a exp ^{f 1 +} x 11 du d Z = -ⁿ q ( x )• ⁽³⁴⁾ ζ- x λ            λ            θ

- 10

Решение СИУ (34) проведено методом коллокаций. Искомая функция ϕ ( ζ ) была задана как произведение двух множителей, где первый множитель обеспечивал явное выделение сингулярности, а второй представлял собой линейную комбинацию T_k ( ζ ) полиномов Чебышева первого рода. Точками коллокации выбраны корни полиномов Чебышева.

Найденная функция разрыва ϕ ( x ) , позволила найти значение коэффициента интенсивности K I нормальных напряжений в окрестности вершин трещины:

K I =± l im 0 ( ф ( x )( 1 ± x ) 1 ² ) •            (35)

Выявлена зависимость точности найденного решения между числом точек коллокаций и величиной искусственно введенного безразмерного параметра к :

к = l/ ( a + 1 ), (36)

характеризующего размер трещины и ее положение относительно вершины клина. Точность решения уменьшается с ростом значения к . Проведенные численные эксперименты позволили сделать вывод: решение уравнения (34) с ошибкой до 5 % для к = 0,75 обеспечивается не менее чем 10 точками; для к = 0,55 требуется не менее 5 точек при той же точности решения.

Результаты вычислительного эксперимента

Ввиду того что построенное решение зависит от многих параметров задачи, определяющих геометрию сечения и физические свойства материалов, представленные выводы имеют качественно-обобщенное значение.

Для каждого конкретного набора параметров задачи в ходе вычислительного эксперимента рассчитывалась величина N , названная индикатором сдерживающего воздействия покрытия, определяемая как отношение коэффициента интенсивности K_I нормальных напряжений в окрестности вершин трещины для модели с покрытием к аналогичному коэффициенту для модели с такими же параметрами, но без покрытия [29]. Значения индикатора на ближней и дальней от угловой точки области вершинах трещины обозначаем соответственно N ( - 1) и N ( + 1).

В качестве основного материала во всех исследованных моделях использован чугун, широко применяемый в станкостроении благодаря своим технологическим характеристикам. Для усиления сечения сторон клиновидной области были рассмотрены следующие материалы: алюминий (Al), никель (Ni), хром (Cr), нитрид титана (TiN), карбид вольфрама (WC). Используемые при расчетах механические параметры материалов приведены в табл. 1.

Таблица 1

Механические параметры материалов

Table 1

Mechanical parameters of materials

Название	Обозначение	Коэффициент Пуассона ( V )	Модуль упругости (Е), ГПа
Чугун	СЧ	0,27	160
Алюминий	Al	0,34	70
Никель	Ni	0,28	204
Хром	Cr	0,35	288
Нитрид титана	TiN	0,28	361
Карбид вольфрама	WC	0,26	532

Относительное расстояние от вершины клиновидной области до трещины определяется безразмерным параметром к: к = l/ (a +1), где l = (b - a )/2( a, b) -координаты концов трещины, показаны на рис.1). Чем ближе значение к к единице, тем ближе трещина расположена к вершине клина. На рис. 2 представлены результаты расчетов зависимости индикатора сдерживающего воздействия покрытия N от расположения трещины относительно вершины клина. Модуль упругости покрытия E1 , характеризующий его жесткость, будем сравнивать с модулем упругости основного материала E исследуемой области. Исследованы покрытия разной жесткости, такие как алюминий (менее жесткий) и никель, хром, нитрид титана, карбид вольфрама и другие (более жесткие). Выявлено, что жесткость покрытия влияет на амплитуду раскрытия трещины. Покрытия с жесткостью меньшей, чем жесткость основного материала исследуемой области, слабо сдерживают раскрытие трещины, толщина таких покрытий не является параметром, препятствующим раскрытию трещины. В частности, непосредственные вычисления показывают, что в случае материала покрытия – алюминий – значения индикатора сдерживания при увеличении толщины покрытия в 10 раз различаются не более чем на 1 %. В случаях более жесткого покрытия его толщина есть параметр, оказывающий воздействие на раскрытие трещины. Чем больше толщина покрытия, тем более выражен сдерживающий эффект. На рис. 3 и 4 показан данный эффект для материала покрытия – хром.

Исследовано влияние угла раствора клиновидной области на индикатор сдерживания, результаты вычислительного эксперимента представлены на рис. 5 и 6. В представленной модели на рис. 5 покрытие – алюминий, его относительная толщина h/l = 0,04. На рис. 6 покрытие – карбид вольфрама, его относительная толщина h/l = 0,01. Расположение трещины определяется параметром к ( к = 0,7; 0,6; 0,5; 0,4; 0,3). Значения координат концов трещины для указанных параметров приведены в табл. 2.

Таблица 2

Координаты концов трещины, соответствующие безразмерному параметр к

Coordinates of crack ends corresponding to the dimensionless parameter к

Table 2

к	a	b
0,3	0,233	0,433
0,4	0,150	0,350
0,5	0,100	0,300
0,6	0,067	0,267
0,7	0,043	0,243

Выявлено, что величина угла раствора клина влияет на процесс раскрытия трещины. Чем меньше угол раствора клина, тем больше покрытие препятствует раскрытию трещины.

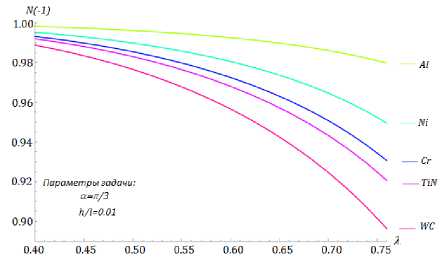
Рис. 2. Влияние положения трещины на значение величины индикатора сдерживающего воздействия покрытия N ( - 1) для разных случаев материала покрытия, при его относительной толщине h/l = 0,01 и угле раскрытия клина а = п/ 3

• Fig. 2.    Influence of crack position on the value of the coating impact indicator value N ( - 1) for different cases of pavement material, its relative thickness h/l = 0,01 and wedge opening angle а = п/ 3

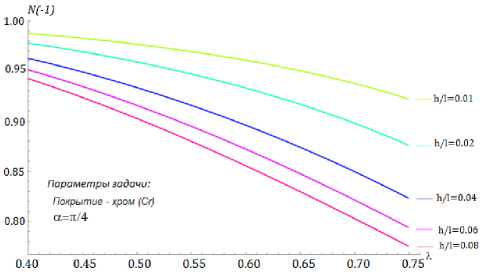
Рис. 3. Влияние положения трещины на значение величины индикатора сдерживающего воздействия покрытия N ( - 1) для разных случаев относительной толщины покрытия hl . Угол раскрытия клина а = п/ 4 . Материал покрытия - хром

• Fig. 3.    Influence of crack position on the value of the coating impact indicator value N ( - 1) for different cases of relative coating thickness h/l . The wedge opening angle а = п/ 4. The coating material is chromium

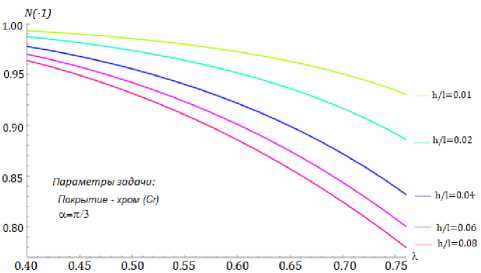
Рис. 4. Влияние положения трещины на значение величины индикатора сдерживающего воздействия покрытия N ( - 1) для разных случаев относительной толщины покрытия hl . Угол раскрытия клина а = п/ 3 . Материал покрытия - хром

• Fig. 4.    Influence of crack position on the value of the coating impact indicator value N ( - 1) for different cases of relative coating thickness h/l . The wedge opening angle а = п/ 3. The coating material is chromium

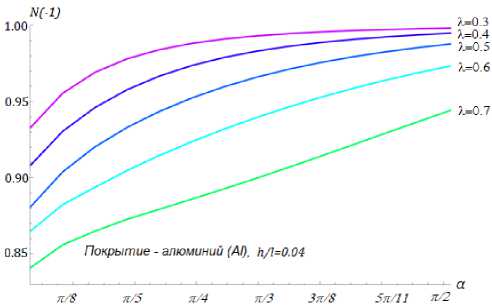
Рис. 5. Влияние угла раствора клина на значение величины индикатора сдерживающего воздействия покрытия N ( - 1) для разных случаев расположения трещины. Материал покрытия – алюминий, его относительная толщина h/l = 0,04

• Fig. 5.    Influence of the wedge solution angle on the value of the coating impact indicator value N ( - 1) for different crack location cases. The coating material is aluminum, its relative thickness h/l = 0,04

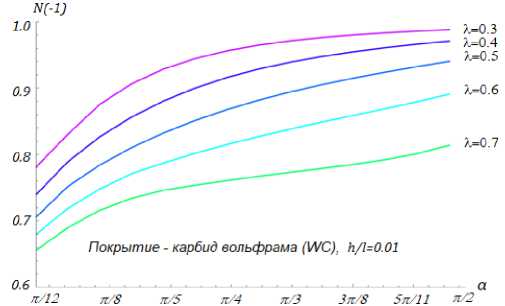
Рис. 6. Влияние угла раствора клина на значение величины индикатора сдерживающего воздействия покрытия N ( - 1) для разных случаев расположения трещины. Материал покрытия – карбид вольфрама, его относительная толщина h/l = 0,01

• Fig. 6.    Influence of the wedge solution angle on the value of the coating impact indicator value N ( - 1) for different crack location cases. The coating material is tungsten carbide, its relative thickness h/l = 0,01

В рамках проведенных исследований влияния усиления сторон клиновидной области на раскрытие трещины изучено влияние толщины и жесткости покрытия, удаление трещины от вершины клиновидной области, раскрытие угла клина на поведение индикатора сдерживающего воздействия покрытия. В процессе реализации вычислительного эксперимента исследована относительная толщина покрытия в пределах от 0,01 до 0,10; жесткость материала покрытия варьируется от мягкой – алюминия – до жесткой – карбид вольфрама, по отношению к основному материалу исследуемой области – чугуну.

Заключение

Результаты исследования позволяют сформулировать следующие выводы:

• –    сформулированная задача применением метода интегральных преобразований и адекватной математической модели покрытия сведена к решению сингулярного интегрального уравнения с ядром Коши;

• –    проведенные вычисления показали, что для жестких покрытий снижение интенсивности напряжений на концах трещины в рассматриваемой задаче обусловлено следующими факторами: увеличение толщины покрытия; уменьшение угла раствора клиновидной области;