Равновесные цены для провайдеров в системе с очередями

Конкуренция среди сервисов, предлагающих свои услуги, является предметом исследования в ряде работ, например [3]. Модель, описывающая такую ситуацию, состоит из двух этапов. Сначала для любого множества цен, установленных провайдерами, пользователи выбирают сервисы согласно какому-то правилу. Учитывая эту информацию, провайдеры назначают цены, и достигается равновесие [2].

В данной работе проведено исследование «системы очередей с дополнительной услугой», в которой у одного из провайдеров появляется конкурент, то есть у пользователей возникает возможность выбора. В этом состоит отличие от рассмотренной ранее модели [4].

В качестве примера к задаче рассмотрен парковочный сервис. Пользователь паркует свою машину на стоянке, чтобы затем воспользоваться услугами другого сервиса. Согласно этому примеру, провайдер, который предоставляет место на парковке, - «parking-provider» (далее -«парковщик»), а другой - «service-provider» (далее - «сервис»). Схематически данная модель представлена на рисунке.

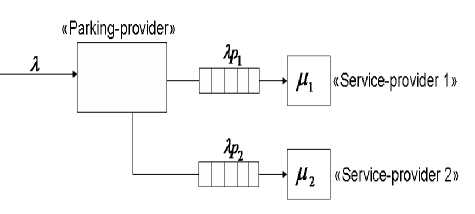
Схема поступления заявок в систему

Здесь X - интенсивность входного потока пользователей, ц - время обслуживания отдельного требования, p 1 - вероятность того, что пользователь решит воспользоваться услугами первого сервиса, p ₂ - второго, p 1 + p ₂ = 1.

В работе исследуется равновесное решение модели. Проведен анализ двух ценовых ситуаций и изменений доходов провайдеров в них. Также определены критерии, которые влияют на выбор пользователя.

МОДЕЛЬ

Будем рассматривать случай, когда провайдеры хотят максимально увеличить свою прибыль. Когда пользователь прибывает в систему, он решает, услугами какого сервиса ему воспользоваться. Если ожидаемый доход пользователя больше нуля, провайдеры увеличивают цены (чтобы при этом количество пользователей не сократилось) до тех пор, пока этот доход не станет равным нулю.

Прежде чем приступить к решению задачи, введем некоторые предположения.

• 1.    Стационарный Пуассоновский поток пользователей с параметром Л прибывает на серверную станцию. Все пользователи идентичны, отлично только время их прибытия. Л - интенсивность, которая необходима для того, чтобы сервис существовал, это необязательно действительная интенсивность входного потока пользователей (которая дальше будет определена как X ).

• 2.    Время обслуживания отдельного требования (заявки пользователя) - экспоненциально распределенная случайная величина с параметром ц , независимая от совокупности моментов событий входящего потока и времен обслуживания других требований.

• 3.    При удачном завершении сервиса каждый пользователь получает доход R (доход выражается в денежных единицах).

• 4.    Стоимость единицы времени пребывания в системе для пользователя равна С.

• 5.    У пользователей нет предпочтений при выборе провайдера. Их цель - сократить расходы при получении сервиса.

• 6.    Предполагается, что пользователь решает присоединиться к очереди или нет, если никто

• 7.    Когда пользователь хочет получить сервис, он не знает размер очереди. Решение о том, при

другой не присоединяется (когда он платит толь-C ко за время своего обслуживания), то есть R > —.

А

соединиться к очереди или нет, он принимает безвозвратно.

Будем рассматривать систему, которая состоит из двух подсистем M/M/1 [1]. Эта система с неограниченной очередью, все заявки обслуживаются в порядке поступления.

Используем следующие обозначения: X - интенсивность входного потока, X = X 1 + X ₂ , X 1 = Xp ₁ , X ₂ = Xp ₂ ; X * - естественное равновесие; i - номер сервиса, i = 1, 2; m i = m i ( X i ) - ожидаемое время пребывания пользователя в системе, учитывая интенсивность поступления X , m i = —¹— ; P. - ¹          а - X i ^S1

цена, назначенная сервисом i ; P N - цена за 1 минуту, назначенная парковщиком; U - ожидаемая прибыль присоединившегося пользователя, воспользовавшегося сервисом i , U = R - P _Si - m i P _N - m i C; nS. - ожидаемая прибыль за единицу времени для сервиса i , n S. = X . P _Si ; n N - ожидаемая прибыль за единицу времени для парковщика, ⁿN = ^{( X} 1 ^m 1 ^{+ X} 2 ^m 2^)PN^.

Далее рассмотрим модель с фиксированным значением p i , i = 1, 2. Разберем два случая: симметричный, когда значение ц одинаково для обоих сервисов, и несимметричный, когда это значение различно.

СИММЕТРИЧНЫЙ СЛУЧАЙ

—

Пусть X = 2 а V

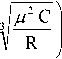
< л. Если X* > Л, то часть заявок не будет обслужена и покинет систему.

Теорема 1 .

Существует единственное положение равновесия, где X = X *,

1                           CR2

^(У 1    ^ 2                        I , ^Ps1 = ^PS2 = ^R 3

А О-2 p ) + 2 p^           ^A

P N = 3 A ^C2 R ^{— C} , ⁿ S 1 = ⁿ S 2 = ² p 1 ⁽T R A ^— 6 ^{RC 2} A ) ,

4 p , (V a C²R — C)

X p i = А ^—

P n + C R — P si .

Заметим, что для того чтобы Xp. > 0, должно выполняться условие: ц P _Si + P _N <  ц R - C. Несложно проверить, что выполнение данного условия для равновесных цен (6) и (7) эквивалентно предположению 6.

Используя (1) и определения n S ₁ , n S ₂ , n N , получим:

(   P + C 1

ⁿ Si = ^X p i P S, = P si I ^{A —} у        I            ⁽²⁾

V     ^{R — P}Si J

^П N   ^{( X p} 1 ^m i ^{+ X p} 2 ^m 2 ) ^PN  ^PN

_— P n + C ¹ R — P S 1

^A R — P S 1 J P n + C

A

P n + C 1 R — P s 2 '

R — P S 2 J P_N + C

Максимизируем n_Si по отношению к P si и n N по отношению к P _N , получаем стратегии

P S 1 = P S 2 = R — , ^R (P n + C)            (4)

\ A

и

P n = ^ ^C2 ^A (2R — P s, — P s2 ) — C.        (5)

Стратегии P S ₁ = P S ₂ = R +. /R(P_N + C) ,

V A

— C A (2R — P s1

P

N

— Ps2) — C не удовлетворяют ус- ловиям задачи.

Получаем

P S 1 = P S 2 = R — ³ ----- (6)

’ A

и

P n = V A C²R — C.                  (7)

Нетрудно проверить, что n S ₁ , n S ₂ , n N принимают максимальные значения в P _S1 , P _S2 , P _N соответственно. Подставляя (6) и (7) в уравнения (1)-(3), получаем:

А с

X p 1 = X p 2 = А ^{— 3}3       , p 1 = p 2 .

R

Соответственно:

Г

X = X p j + X p ₂ = 2 а

V

—

3^2= 1

N R J

X 1 = X 2 = 2 p 1 а —

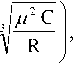
^ 1 = ^ 2 =------------ i= ,

A ^{(1 — 2} p 1 ) ^{+ 2} p h/ ^ c

R

n_{S 1} = n_{S 2} = 2 p ₁ ( ^RA — V RC² A ) ,   (10)

_      4 p 1 ( 3 u C 2 R - C)

ⁿN =              I —2—

U ⁽1 ^— 2 p i ) + 2 p ■ 3 "^C R

Полученные результаты показывают, что на стоимость услуг сервисов никак не влияют p 1 , p . Значение p i влияет только на конечную прибыль сервисов.

Для парковщика выгодно появление второго сервиса, так как увеличивается количество пользователей в системе, соответственно, доход парковщика также растет. Пользователям это также выгодно, так как у них появляется возможность выбора, а время их пребывания в системе может сократиться. При этом большее количество пользователей могут воспользоваться услугами.

НЕСИММЕТРИЧНЫЙ СЛУЧАЙ

Допустим, что интенсивность обработки заявок у сервисов различна. Посмотрим, как изменится стоимость услуг в данном случае.

Пусть X = ц 1 + и 2

-

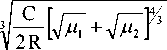
<Л .

Теорема 2.

Существует единственное положение равновесия, где X = X*,

® i

U i

= R

P N

P Si

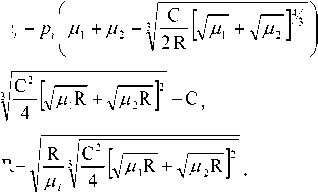
R ₃

R -

ⁿ Si = P i

ⁿ N =

x

x

—

2 + Z

i = 1

U i

/

x U 1 + U ₂

—

U i

V

-

C

x

—

pi

U i

Доказательство теоремы 2 проводится по аналогии с доказательством теоремы 1. Разница в том, что теперь у каждого сервиса свое время обслуживания отдельного требования, то есть в данном случае ц 1 = ц ₂ .

Полученные результаты подтверждают, что на стоимость услуг значительно влияет интенсивность обработки заявок; чем выше это значение, тем стоимость услуг у сервисов выше, и наоборот. Соответственно, и доход сервисов может возрасти, если количество пользователей не сократится. Доходы парковщика не уменьшатся в силу того, что количество пользователей возрастет. Стоимость услуг парковщика может сократиться в силу изменения количества пользователей. Однако первому сервису невыгодно появление конкурента, так как теперь, чтобы поток пользователей не сократился, необходимо или понижать цену, или наращивать мощность сервера. При этом доход сервиса теперь зависит от мощности сервера конкурента, а борьба за цены разворачивается между тремя провайдерами. Это не всегда бывает выгодно сервису.

У пользователей появляется возможность выбора: либо пользоваться услугами более дорогого сервиса, либо более дешевого, но при этом больше платить парковщику. Однако распределение пользователей по каналам p ₁ , p ₂ по-прежнему не влияет на уровень цен. Значение p_i влияет только на конечную прибыль сервисов; чем выше это значение, тем выше их доход. Причем в зависимости от величины p i прибыль сервиса i может быть как больше, так и меньше, чем в условиях монополии [4]. Однако в таком случае очередь из пользователей возрастает, увеличивается время обслуживания и нагрузка на сервер также растет.

ЗАКЛЮЧЕНИЕ

Было проведено исследование модели конкурентной борьбы между сервисами. Рассмотрены две ценовые ситуации и определено, как выбор пользователей зависит от стоимости услуг провайдеров. Также найдены равновесные цены для сервисов и, соответственно, их доходы. Проведено сравнение полученных результатов с моделью без конкуренции; подтверждено, что появление второго сервиса выгодно пользователям и невыгодно первому сервису.

БЛАГОДАРНОСТЬ

Выражаю благодарность профессору В. В. Мазалову за постановку задачи и помощь при подготовке статьи.