Равновесные модели экономики в период мирового финансового кризиса

• I.    Особенности текущего мирового финансового кризиса

  Текущий глобальный экономический кризис — это суровый полигон для испы-

  Рис. 1. Развитие мирового финансового кризиса

  
  

  — Период 1992–1999 гг. был периодом процветания американской экономики, когда США импортировали мозги и успешно экспортировали технологии. Материальные ресурсы покупались за границей, а основная масса населения занималась обслуживанием друг друга.

— В 2000 г. выяснилось, что ввиду насыщения рынков развитие информационных и телекоммуникационных технологий (ИТ) уже не способно «тянуть за собой» всю американскую экономику — рост курса акций ИТ-компаний обернулся «пузы- таний методов моделирования экономики, поскольку в экономических процессах наблюдается резкий слом сложившихся тенденций. Если рассматривать события кризиса последовательно, они кажутся вполне понятными (рис. 1).

рем». Однако этот пузырь был образцово «сдут» за счёт скупки своих акций крупными компаниями следующего уровня новизны технологий.

После был применен монетарный метод стимулирования экономики — снижение процентной ставки в расчёте на то, что какая-нибудь другая отрасль пойдет в рост за счёт дешевых денег. Но такой отрасли не нашлось несмотря на то, что учётная ставка, то есть процент, под который Федеральная резервная система (ФРС, центральный банк США) кредиту- ет коммерческие банки, была снижена в 7.5 раз!

— Догматически доведя до абсурда в 2000–2003 гг. политику монетарного стимулирования экономики и не достигнув успеха, власти США фактически обратились к, казалось бы, навсегда отвергнутым в 1980-е гг. кейнсианским методам стимулирования за счёт увеличения бюджетного дефицита: началась война в Ира-ке ¹ (2003 г.).

— Кейнсианский метод сработал — в 2004–2006 гг. экономика (и процент) начали расти. Но этот искусственный рост не был подхвачен другими отраслями, и ипотечные кредиты, набранные в период низких процентных ставок, оказались невозвратными.

— Ипотечный кризис 2006 г. был смягчен и «размазан» производными бумагами, которые диверсифицируют риски вложений — убытки от ипотеки были временно компенсированы доходами от бурного роста цен на ресурсы (нефть, металлы, продовольствие).

— В 2008 г. рост рынков ресурсов тоже обернулся пузырем, который уже нечем было скомпенсировать. Началось падение экономики в мировом масштабе.

Эта логичная картина, однако, оказывается гораздо более странной, если взглянуть на неё в целом, так сказать, «сбоку». Ключевой момент, с нашей точки зрения, состоит в том, что ни монетарное, ни кейнсианское стимулирования не открыли нового «мотора» в экономике США ² , такого, какими были автомобили в 1920-х, дороги и дома в 1930-х, самолёты в 1950-х, ЭВМ в 1960-х, ракеты в 1970-х, ПЭВМ в 1980-х, телекоммуникации в 1990-х. А это значит, что случился совсем не тот кризис, какого ждали!

Все ожидали кризиса возможностей (исчерпания ресурсов), а случился кризис потребностей (исчерпание стимулов к росту). Экономика «золотого миллиарда» физически расти может, но не хочет! При этом виртуальная экономика оказалась устойчивее реальной — продовольствие, топливо, металлы, золото оказались избыточными и потеряли в цене гораздо больше, чем услуги и информация. Даже в финансовой области рухнуло то, что испо-кон веков считалось самым надежным вложением — ипотека, то есть кредит реальному лицу под реальный залог, а, например, кредиты на раскрутку сайтов с рекламой пока что выплачиваются. Чем дальше в технологической цепочке от базовых отраслей находится производство, тем меньше оно страдает от кризиса.

Причина та же, по какой двух-трёх-кратное изменение цен на энергию и металлы почти не сказывается на цене автомобилей. В себестоимости современного автомобиля расходы на дизайн, контроль качества и рекламу составляют гораздо большую долю, нежели материальные затраты. Тот новый продукт, за который люди готовы платить деньги (добавленная стоимость), создаётся нынче не столько на поле или фабрике, сколько в КБ, ОТК и магазине [1].

Сейчас трудно сказать, чем все это может кончиться, особенно если учесть важное наблюдение С.П. Капицы, что нынешний кризис совпадает с беспрецедентным в истории человечества явлением: рост населения Земли замедляется без голодовок и эпидемий! Я не исключаю, что человечество переходит к нулевому росту и чисто «духовной» жизни. Конечно, не к таким, какими их представляли себе экологи и моралисты. Просто совокупное материальное потребление стабилизируется, и человечество теряет интерес к внешнему миру, сосредотачиваясь на неисчерпаемых проблемах межличностных отношений ³ .

Впрочем, до этого ещё далеко, хотя бы потому, что сложившаяся нынче система экономических механизмов работоспособна только при наличии перспективы экономического роста. Так что в обозримом будущем либо рост все-таки восстановится, либо последует череда неудачных попыток его восстановить. И пока не возникли и не проявились новые механизмы, адаптированные к нулевому росту, можно всерьез моделировать только процессы спада и восстановления роста.

• II.    Системный анализ развивающейся экономики

  Экономика — подсистема общества, управляющая производством, распределением и потреблением благ: ресурсов, товаров и услуг. Задача, которую должна решить современная экономика, чудовищно сложна. Речь идёт о производстве миллиардов видов благ и их распределении между миллиардами физических и юридических лиц. По этой причине экономика как управляющая система всегда достаточно децентрализована. Напомним, что вопреки иногда звучащим утверждениям, что «в СССР планировалось все, до гвоздя», Госплан оперировал всего примерно 2000 наименований продукции, в то время как в 1970-е гг. реальная их номенклатура превышала сотню миллионов. Именно катастрофическое несоответствие средств управления и наблюдения стремительно возрастающей сложности экономических связей было, по нашему мнению, главной причиной провала идеи централизованного планирования.

Итак, моделируя экономику, мы имеем дело со сложной системой. Сложные системы, такие, как Вселенная в целом, биосфера, отдельный живой организм, человеческий индивидуум, естественный язык, экономика, выделяются не просто тем, что состоят из очень большого числа элементов, а прежде всего своей уникальностью и, самое главное, способностью к качественным изменениям. Поэтому, изучая сложную систему, мы фактически наблюдаем единственную траекторию, которая не воспроизводит себя статистически достоверно и не показывает всех потенциальных возможностей системы. Тем самым мы выходим за рамки эмпирического метода — основы успеха естественных наук. Не удиви-

ТРУДЫ МФТИ. — 2009. — Том 1, № 4 тельно, что успехи в моделировании сложных систем пока значительно скромнее, чем успехи моделирования, скажем, технических систем.

Для сложных систем невозможны эксперимент и массовое наблюдение. Поэтому ни для одной сложной системы до сих пор не создано универсальной модели, из которой все остальные следовали бы как частные случаи, подобно тому как, скажем, модели радиотехнических устройств следуют из теоретической модели электродинамики. Приходится иметь дело с множеством моделей одной и той же системы, каждая из которых использует свой язык понятий и рассматривает систему в своём ракурсе, пренебрегая отнюдь не малыми величинами [3]. Если модели физических систем должны объяснить результаты сделанных и предсказывать результаты планируемых экспериментов, то модели сложных систем призваны в первую очередь заменить эксперимент. Существует не просто множество моделей экономики, но и множество методических подходов к её моделированию.

C 1990-х гг. наиболее популярными стали вычислимые модели общего равновесия (CGE) (см., например, [4, 5, 9]), поскольку выяснилось, что учёта одних технологических ограничений (балансовые модели [6]), экстраполяции предыдущих тенденций (эконометрические модели [7]) и прямолинейного наложения внешних ограничений (модели системной динамики [8]) недостаточно для адекватного описания современной экономики. CGE модели восходят к динамической версии модели общего экономического равновесия К. Эрроу и Дж. Дебре [10: Arrow, Debreu] (см. разд. 3.3). Модели общего равновесия, особенно динамические, сложны, поскольку представляют собой целую связку нелинейных задач оптимизации поведения (см. разд. 3.6). В CGE моделях динамические связи обычно описываются феноменологически предположениями.

Здесь следует заметить, что современной науке термин «равновесие» используется в трёх исходно различных смыслах, а именно как:

• 1)    динамическое равновесие, то есть баланс сил, действующих на систему;

• 2)    статистическое равновесие, то есть баланс вероятностей переходов между состояниями системы;

• 3)    экономическое равновесие (или, более обще, теоретико-игровое равновесие по Нэшу), то есть баланс интересов субъектов конфликта.

Что-то общее между этими понятиями безусловно, есть, но до сих пор никому не удалось аккуратно проследить эту связь в достаточно общем виде ⁴ . Поэтому обычное для околонаучных рассуждений смешение этих понятий является недопустимой вульгаризацией. В частности, как мы наглядно покажем ниже, экономическое равновесие не подразумевает никакой статичности или простоты динамики.

В 1975 году в Вычислительном центре АН СССР (потом РАН) возникло новое направление исследований: системный анализ развивающейся экономики (САРЭ), в котором методология математического моделирования сложных систем, развитая в естественных науках, была синтезирована с достижениями современной экономической теории [11]. Модели системного анализа развивающейся экономики по смыслу близки к CGE моделям, но больше обращают внимания на специфику сложившихся экономических отношений, да и начались наши исследования лет на 15 раньше появления первых CGE моделей.

К исследованиям приступили с моделей рыночной экономики, а в 1988 г. была построена модель, которая воспроизводила основные качественные особенности эволюции плановой экономики. Поэтому к моменту начала экономических преобразований в СССР, а затем в России уже был разработан подход к анализу происходивших в экономике изменений. В частности, за два года до реформы 1992 г. были правильно предсказаны краткосрочные её последствия. Каждая из последующих моделей:

• —    модель экономики периода высокой инфляции 1992–1995 гг.;

• —    модель экономики периода «финансовой стабилизации» 1995–1998 гг., предсказавшая кризис 1998 г.;

• —    модель для оценки перспектив развития экономики после кризиса 1998 г. — была основана на системе гипотез относи-

• тельно характера тех экономических отношений, которые складывались в соответствующий период в России.

С помощью моделей удалось понять внутреннюю логику развития экономических процессов, скрывшуюся за видимой, часто, казалось бы, парадоксальной, картиной экономических явлений, которая не укладывалась в известные теоретические схемы. Опыт применения моделей показал, что они служат надежным инструментом анализа макроэкономических закономерностей, а также прогноза последствий макроэкономических решений при условии сохранения сложившихся отношений. Можно сказать, получилась целая «летопись» российских экономических реформ, выраженная языком математических моделей. Эти модели детально описаны в [13, 14], а подробный обзор дан в [15, 16].

Главная трудность моделирования советской и российской экономики в период 1986–2004 гг. была в том, что вследствие её эволюции каждую следующую модель приходилось создавать заново, начиная с системного анализа изменившихся экономических отношений. Создание новой модели — очень трудоемкое дело, оно занимает примерно год работы коллектива квалифицированных специалистов. Но даже не в этом главное. Новые экономические отношения описываются новыми переменными, другими соотношениями, часто требуют использования новых математических методов. Поэтому нельзя сказать, что в итоге почти тридцатилетних исследований эволюции советской и российской экономики мы создали систему моделей. Перечисленные выше модели трудно сопоставить друг с другом так же, как трудно сопоставлять модели, созданные разными исследовательскими группами. Такое положение дел, увы, типично для моделирования сложных систем [17].

В 2004 г. в рамках САРЭ мы несколько изменили подход к моделированию, а именно отказались от характерного для CGE моделей и ранних моделей САРЭ упрощения динамических связей и обратились к теоретически более последовательной, но технически и концептуально гораздо более сложной конструкции межвременного равновесия с управлением капита- лом [16]. Обсудим её положение в рамках вопроса о подходах к моделированию экономики.

• III.    Принципы построения моделей взаимодействия агентов

Разногласия в экономической теории и сложность конкретных моделей часто создают у представителей смежных специальностей впечатление об отсутствии в практике моделирования экономики общих принципов. Однако по крайней мере для моделей экономики, основанных на описании взаимодействия агентов (CGE и САРЭ), можно указать иерархию принципов-предположений, идущую от более общих, принимаемых почти во всех моделях, к более специальным и заканчивающуюся теми моделями, которые мы сейчас пытаемся применить для моделирования российской экономики в условиях мирового кризиса.

• III.1.    Система материальных балансов

Подавляющее большинство моделей основывается на следующей картине движения материальных благ:

• 1)    имеется исчерпывающий список N всех агентов (физических и юридических лиц);

• 2)    имеется исчерпывающий список G всех материальных благ (ресурсов, товаров и услуг);

• 3)    в каждый момент времени t весь наличный объём каждого блага разделен между агентами, и изменение запаса Q V ( t ) блага i ∈ G у агента ν ∈ N описывается уравнением баланса (подробнее см. [19]):

dν dt Q i скорость изменения запаса

^X i^ν производство

C i^ν               V i^ν

- конечное - текущие - потребление    затраты

ZV E^h ( h? - h? )

- капитальные - передачи благ . затраты между агентами

Конечно, это описание весьма условно. Списки агентов и благ необозримы ( |N|, |G| ~ 10 9 ) и постоянно меняются по составу. Тем не менее до сих пор вся бухгалтерия и вся экономическая статистика строятся на основе приведённой схемы. Ее сила в том, что она последним членом в правой части выражает фундаментальное свойство аддитивности блага: агент ν теряет то, что получает от него агент μ . Благодаря этому распределение запасов по агентам оказывается мерой на множестве агентов, и суммарный запас любого множества агентов удовлетворяет уравнению баланса того же вида [19].

Впрочем, в будущем от системы материальных балансов, возможно, придётся отказаться. Дело в том, что все большую роль в экономике играют два класса неаддитивных благ:

— общественные блага (порядок, справедливость, безопасность, экологический комфорт и т. п.) не делятся между агентами. Они (в идеале) есть либо у всех одновременно, либо ни у кого;

— информационные блага не складываются из частей. Если агент ν сообщает агенту μ новость, то агент ν эту новость не забывает, а повторное сообщение той же новости ничего не даёт агенту μ .

Наличие неаддитивных благ представляет огромную трудность как для экономической теории, так и для экономической практики. Проблема с общественными благами решается выделением особого единого производителя этих благ, называемого государством ⁵ , у которого остальные агенты покупают эти блага не по частям, а вскладчину (за налоги [10: Public Goods]).

Проблема информационных благ остаётся нерешённой6 . Пока что бухгалтерия «втискивает» информационные блага в состав услуг, а потом мучается с оценкой нематериальных активов. Теория же приходит к выводу, что для адекватного учёта информационных благ следует менять ни много, ни мало, как саму арифметику [20]!

III.2. Система финансовых балансов

Запутанная система материальных балансов требует агрегирования информации о бесчисленных разнородных материальных благах. И нужно это в первую очередь не исследователю экономики, а самому человеку, живущему в ней. Не удивительно, что средство агрегирования появилось давным-давно, и его описание составляет следующую общую составляющую большинства моделей, правда, уже менее распространенную, чем материальные балансы.

Свертывание и передачу информации в экономике осуществляют деньги. В сколь-нибудь развитой экономике каждому систематически повторяющемуся потоку обмена h _i ^νμ в (1) отвечает встречный денежный поток платежей:

Н Г ( t ) = P i ( t ) h? ( t ) , (2) в котором, как можно считать, цена pi ( t ) не зависит от того, какая пара агентов совершает обмен (подробнее см. [19]). Умножая балансы на цены (1) и складывая по группам агентов и продуктов, получаем описание потоков агрегированных благ между макроагентами. В частности, сложение по товарам и услугам i ∈ P ⊂ G , но без ресурсов, и по агентам ν ∈ S ⊂ N , расположенным на территории некоторой страны, даёт основной макроэкономический баланс этой страны:

Запасы (остатки) денег у агентов W ^ν — аддитивная величина. В современных условиях, когда натуральная эмис-сия ⁷ отсутствует, эти запасы удовлетворяют следующему уравнению баланса (подробнее см. [19]):

^dW ^ν dt скорость изменения

запаса денег

+

У У ( Н Г - №Г )

*EN iEG              + платежи

^2 ( T *^v - T ^v* )

μ∈N трансферты

У (d-L-¹*" + *TN d^dt

скорость изменения долгов и сбережений

+

^- dL") У ( R *

+ *EN

- R ^v* )

проценты

Приведение этой дифференциальной связи к нормальной форме превращает её в систему линейных дифференциаль-

ных уравнений, описывающую изменение

остатков различных счетов агента в силу стандартных бухгалтерских двойных про-

водок.

Складывая балансы (4) по всем агентам, получаем, что сумма запасов денег у агентов не растёт со временем! (Потоки денег замкнуты):

d У W ^v ( t ) = 0 .        (5)

у у Pi (X" - V") _ у у Pi С V vES iE?                        vES iE?        +

ВВП          потребление

. У У p . ( Z i + QQ V )

+ VES iE?                + накопление

УУ p i У h V*  УУ P i У h *

+ vES iE? *EN\S     - vES iE? *EN\S экспорт            импорт

Это соотношение вместе с очевидным фактом роста номинальных денежных запасов в мире (хотя бы за счёт инфляции) показывает, что у некоторых агентов (эмитентов) запасы денег должны быть отрицательными. Таким образом, с точки зрения физических аналогий, деньги представляют собой весьма своеобразную материю. Хотя сумма запасов строго сохраняется, изменение этих запасов происходит не только за счёт их перемещения между агентами, но за счёт возникновения отрицательных запасов. Все новые деньги в нынешнем мире возникают в процессе кредитной эмиссии — одновременного увеличения активов (положительных запасов, требований) и пассивов (отрицательных запасов, обязательств) 8 .

Поэтому не стоит ждать, что при крахе одного финансового рынка деньги оттуда перейдут на другой, или искать, кто же «нашел» те миллиарды, которые кто-то потерял при крахе. В кризис активы сокращаются с пассивами, и теряют все — одни выгоду от покупки в кредит, а другие надежду на возврат долга.

Возможность образования финансовых пузырей заложена в самой природе современных денег. Тем не менее в условиях потери состоятельности материальными балансами денежные потоки остаются единственными надежно измеряемыми величинами. Следует не игнорировать якобы «дутые» финансовые показатели, а учиться

• III.3.    Поведение агентов: каноническая форма модели как обобщение идеи экономического равновесия

Следующий более узкий принцип состоит в рассмотрении агентов не просто как узлов графов материальных и финансовых потоков, а как лиц, принимающих решение относительно величины потоков, находящихся в их «компетенции». Уравнения (1), (4) вместе с естественными условиями неотрицательности потоков и запасов (подробнее см. [19]) служат внутренними ограничениями на возможности выбора агентов. Другими внутренними ограничениями могут быть технологические ограничения на возможность преобразования одних благ в другие.

Главная проблема экономики состоит в определении потоков обмена (величинах с двумя верхними индексами в (1), (4)), о размере которых контрагенты должны правильно ими пользоваться.                принять совместное решение.

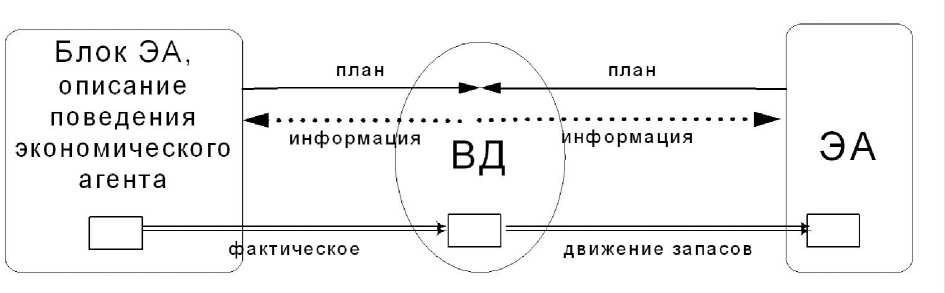
Рис. 2. Схема модели в канонической форме

Идея экономического равновесия состоит в том, что каждый из агентов предлагает свой план величины потока (спрос или предложение на экономическом языке). Этот план условный — он зависит от значений особых информационных переменных (цен, процентов, курсов), которые приносят агенту информацию о состоянии всей системы. Допустимые сложившимися экономическими отношениями планы описываются институциональными (внешними) ограничениями, содержащими информационные переменные. Простейшим при- мером такого ограничения может служить связь (2) между потоками денег H^^ (t) и блага h^ (t) при заданной цене pi (t). Планы агентов согласуются в процессе их взаимодействия так, чтобы по всей системе выполнялись включенные в модель балансовые соотношения.

В общем случае мы приходим к модели в канонической форме [16, 17], схема которой изображена на рис. 2.

Соотношения модели в канонической форме распадаются на блоки двух типов: блоки описания поведения агентов (ЭА)

и блоки описания взаимодействия агентов (ВД). В общем случае взаимодействие не означает реализации планов контрагентов, а иногда сводится просто к обмену информацией между ними [16]. В канонической форме могут быть записаны все модели САРЭ, в том числе и модель плановой экономики [13], а также все CGE модели и большинство имитационных (но далеко не все эконометрические и балансовые). Классификация соотношений в канонической форме модели позволяет проверять её корректность средствами системы ЭКОМОД [16].

Главная задача при создании модели в канонической форме состоит в выборе агрегированных аддитивных величин, для которых записывается полная система материальных и финансовых балансов и запись в терминах этих величин институциональных ограничений, описывающих экономические отношения. Именно формой и набором этих ограничений выражается различие между конкурентными и монопольными рынками [16], различие акционерной и долевой собственности [18], возможность использовать денежные суррогаты [13] и каналы теневого оборота [16]. В системах институциональных ограничений проходит и различие между моделями CGE и САРЭ. Если в первых институциональные ограничения берутся в основном из учебников, то в моделях САРЭ мы стараемся описать этими ограничениями фактически сложившиеся экономические отношения.

• III.4.    Рациональность поведения: представительные индивиды или макроагенты?

Ограничения модели обычно оставляют агенту достаточно большую свободу выбора. В имитационных моделях действия агентов описываются прямым заданием правил принятия решений. Такой подход возможно оправдан при описании «организованной рутины» в рамках корпорации. Но во всей экономической системе, способной к самоорганизации, такое прямое решение «за всех» представляется чересчур самоуверенным, да и модифицировать его без ошибок очень сложно. Поэтому в экономической теории, в CGE моделях и в моделях САРЭ для большинства агентов постулируется рациональное поведение, то есть выбор в рамках ограничений такой стратегии, которая максимизирует некий показатель: полезность, прибыль, капитализацию и т. п.

Это положение постоянно вызывает сомнения у специалистов и резкое отторжение у неспециалистов. Говорят, что экономическая теория слаба потому, что игнорирует «человеческий фактор» и изучает поведение полностью вымышленных «homo economicus». Однако люди — ведь не атомы. Казалось бы, зачем выдумывать за них мотивы и принципы их деятельности, когда можно просто спросить, почему они действуют так, а не иначе? Такие опросы постоянно проводятся, но из них не удаётся сложить целостной картины, а вот взгляд экономистов «со стороны» позволяет заметить определённые закономерности.

Поведение отдельных людей прихотливо и действительно определяется множеством не учитываемых экономической теорией факторов (женился, заболел, «шлея под хвост попала» и т. д.). Представляется, что любой из нас устроен сложнее, чем вся экономика. Поэтому все известные нам попытки основать экономическую теорию на законах психологии полностью провалились, а в экономике мы можем что-то понять только потому, что в ней проявляется лишь малая часть богатства внутреннего мира человека. Происходит это потому, что в экономике люди действуют в условиях безличностных угроз (наказания, увольнения, разорения, морального осуждения и т. д.) В результате их поведение стандартизируется, а индивидуальные различия нивелируются [21].

Остаются, по крайней мере две разные возможности определения субъекта рационального поведения. Существующая теория апеллирует к «репрезентативным агентам», каждый из которых характеризуется заданными неизменными интересами. В микроэкономических исследованиях иногда пытаются выявить формы интересов, но в макроэкономических моделях практически всегда рассматривается один репрезентативный агент каждого типа (потребитель, производитель, торговец и т. д.).

Мы полагаем, что представление об абсолютно автономных «репрезентативных индивидах» противоречит тому, что люди и организации взаимодействуют друг с другом. В рамках крупных групп субъектов, выполняющих сходные роли в экономике, имеют место конкуренция и подражание. В результате коллективное поведение такой группы оказывается более простым и последовательным, чем поведение любого из её членов, и может быть описано как простое стремление к максимизации потребления, прибыли, богатства и т. п., и это можно подтвердить прямыми измерениями. Например, в [22] приведён пример простой эконометрической зависимости, которая в течение долгого времени выполняется для всей российской банковской системы на порядок точнее, чем для любого отдельного банка, в том числе и самого крупного.

Самым ярким подтверждением правильности нашего подхода служат результаты исследований по теории агрегирования и рационализации потребительского спроса, проведённые А.А. Шанани-ным [13].

Имея торговую статистику, то есть временной ряд наборов товаров, купленных какой-то группой потребителей, и ряд цен, по которым данные товары были куплены, можно конструктивно проверить, существует ли вогнутая монотонная однородная функция полезности такая, что наблюдавшиеся покупки служат точками максимума этой функции при бюджетном ограничении и наблюдавшихся ценах ⁹ .Результаты этих проверок таковы:

• —    отдельная семья НЕ имеет функции полезностии даже однозначной функции спроса, зависящей от цен и доходов;

• —    однородный социальный слой (население пригорода Нью-Йорка) как целое НЕ имеет функции полезности, хотя и имеет функцию спроса;

• —    население всей страны (даже такой открытой, как Нидерланды, или такой нестабильной, как Венгрия периода перехода от социализма к капитализму) как целое имеет функцию полезности, которая описывает наблюдаемый годичный спрос

  ТРУДЫ МФТИ. — 2009. — Том 1, № 4 за период порядка 10 лет в разрезе 200–300 продуктов;

— cовокупность покупателей большого магазина имеет функцию полезности, которая описывает наблюдаемый недельный спрос за период нескольких лет в разрезе 2000 продуктов.

Эти удивительные результаты можно объяснить (в том числе и на модельном уровне) тем, что функция полезности не «сидит» в головах потребителей, а рождается в процессе взаимодействия нерациональных потребителей и торговцев, манипулирующих ценами к своей выгоде.

Основываясь на рассуждениях и наблюдениях, мы приписываем интересы макроагентам, то есть считаем интересы просто вариационными принципами, выделяющими наблюдаемое поведение макроагентов из всех вариантов, допускаемых ограничениями модели [12, 19].

Это положение имеет и «обратную силу». Когда мы имеем дело с влиятельным субъектом, наделенным единой волей, например, с государством, не стоит пытаться описывать его действия принципом оптимальности. Лучше просто спросить, что он собирается делать, то есть описывать его поведение сценариями возможных действий.

• III .5. Принцип рациональных ожиданий и типовая задача агента

Приведённых выше принципов достаточно, чтобы построить статическую модель, но для динамической их не достаточно. В динамических моделях агент планирует свои действия на будущее и, значит, должен прогнозировать будущие изменения конъюнктуры (информационных переменных). Возникает парадокс: мы строим модель, чтобы дать прогноз конъюнктуры, а для построения модели надо знать, как агенты конъюнктуру прогнозируют!

Радикальным решением этого парадокса служит принцип рациональных ожиданий [10: Rational Expectations, 23]. Наиболее просто он формулируется так: модельные агенты используют для своих прогно- зов ту самую модель, которую мы строим! Поначалу кажется удивительным, как вообще можно получить что-то нетривиальное. Но фактически это возможно, поскольку набор планируемых переменных у агентов различен и цели их тоже различны.

Хотя принцип рациональных ожиданий резонно вызывает сомнения, поскольку подразумевает, что модельные агенты «знают все наперед» ¹⁰ , мы рискнули применить его к моделированию реальной российской экономики. В результате мы добились успеха большего, чем при упрощении описания поведения агентов, характерном для CGE моделей и ранних моделей САРЭ. Сейчас стали выясняться причины этого успеха (см. заключение).

В детерминированном случае, о котором здесь идёт речь, принцип рациональных ожиданий приводит к модели межвременного экономического равновесия [10: Intertemporal Equilibrium]. В такой модели каждый агент, исходя из своих целей, возможностей и прогнозов, определяет свой спрос и предложение на продукты, ресурсы и финансовые инструменты в текущий и все будущие моменты времени, а потом прогнозы (единые для всех) определяются из условия согласования спроса и предложения опять-таки в текущий и все будущие моменты времени. Модели межвременного равновесия известны давно, но до сих пор они применялись исключительно для изучения некоторых теоретических вопросов на стационарных режимах довольно абстрактных моделей экономики (см. например [24]).

Естественные требования:

— соответствие классической модели экономике совершенной конкуренции Эрроу–Дебре [10: Arrow, Debreu];

— согласованность во времени;

— масштабная инвариантность (см. разд. 3.5) — приводят к конструкции межвременного равновесия с управлением капиталом [16]. Ее мы и кладем сейчас в основу наших моделей. В рамках этой кон- струкции интересы (макро) агентов унифицируются — каждый из них, включая потребителя, стремится максимизировать свою правильно понимаемую капитализа-цию11, и в типичном случае задача (макро) агента a принимает вид следующей задачи оптимального управления [16]:

9 ^a K ^ max (6)

по постоянной 9a > 0, и функциям времени: Wa (скаляр), xa, ya (векторы) на конечном интервале времени [t0 ,T] при ограничениях d-Wa = r(t)жа + p(t)ya - 9av(t),(7)

dt dxa = Rxa + Pya,(8)

g(t,xa,ya,9av,Wa) > 0,(9)

где r ( t ), p ( t ), v ( t ) — суть заданные функции времени, матрицы R , P — постоянны, а g ( t, • , • ,• ) — гладкая, вогнутая, линейнооднородная функция.

xa^g , ya 99, , 9av^9 , Wa     = g dxa    dya     39 av     dWa

К ограничениям (7) –(9) ещё следует доба- вить граничные условия специального вида [16, 25], о которых несколько слов будет сказано ниже.

Величины x ^a имеют смысл запасов материальных благ и остатков финансовых инструментов, а y ^a — смысл потоков, изменяющих эти запасы. Уравнения (8) — это в основном ¹² в той или иной степени агрегированные балансы: материальные (1) и финансовые, полученные нормализацией дифференциальной связи (3). Поэтому уравнения (8) линейны, а элементы матриц R, P по большей части равны 0, 1 или - 1.

Уравнение (7) представляет основной финансовый баланс агента (3) после нормализации и учёта ограничений типа (2). Соответственно, r (t) — доходности или процентные ставки, а p(t) — рыночные цены или курсы. Последний член в (7) специфичен для модели межвременного равновесия с управлением капиталом. Он описывает поток полезных расходов (потребительские расходы для домохозяйств, дивиденды для фирм), который агент фактически стремится максимизировать (см. (6)). Почему при определённом выборе постоянной K величину θaK можно рассматривать как оценку капитализации агента, подробно рассказано в [16].

Условия (9) объединяют все технологические и институциональные ограничения, оставшиеся после исключения простых связей типа (2). Предположение об однородности (10) присутствует в подавляющем большинстве динамических моделей экономики. Его эмпирическим обоснованием можно считать то обстоятельство, что в экономике пока не обнаружено ни «мировых постоянных», ни «естественных единиц измерения». Наглядным подтверждением последнего служит то, что изменения в физическом мире мы обычно характеризуем скоростями, а изменения экономических показателей — темпами роста. Это означает, что в первом случае абсолютные масштабы величин существенны, а во втором — нет.

• III .6. Физические аналоги и магистральное свойство задачи агента

Задача агента (6) –(9) — неавтономная задача оптимального управления со смешанными ограничениями. Поскольку в конечном счете нам нужны решения этой задачи не при произвольных, а при равновесных, то есть согласованных с решением, внешних воздействиях r ( t ) , p ( t ), считаем возможным обойтись достаточными условиями оптимальности в форме Лагранжа, считая двойственные переменные к ограничениям (7) -(9): i " ,7 a и p a 7 0, соответственно достаточно регулярными функциями времени (а не мерами). Двойственные оценки активов x ^a , приведённые к деньгам Ф a преобразованием

a

7 a = Ъ         (И)

ξa имеют смысл объективно обусловленных цен активов xa для агента a.

Как известно, условия оптимальности можно записать как гамильтонову систему относительно наборов прямых (фазовых) q = ( Ф " — " ) и двойственных (сопряженных) переменных

А = (i"7") 7 = dHa(t,q,7A), dt ∂λ dA = dt

- ^dH a ( t,q,A ) ∂q

Это вызывает ассоциацию из физики: «Динамическая система, типичные решения которой суть обратимые колебания или вращения вокруг положений равновесия с сохранением величин, связанных с симметриями системы». Однако в экономических приложениях обратимости, как правило, нет ввиду наличия неголономных связей (9); полная энергия H не сохраняется ввиду неавтономности системы, а симметрий ожидать не приходится, поскольку набор фазовых переменных xa — собствен- но, не вектор, а список разнородных вели-чин13.

Впрочем, есть отмеченная выше масштабная симметрия относительно экстенсивных переменных — потоков и запасов материальных благ и финансовых инструментов (10). В полном соответствии с теоремой Нетер данной симметрии отвечает первый интеграл ¹⁴ i " W a + 7 " — " системы (12). После приведения к деньгам интеграл приобретает экономический смысл собственного капитала агента (оценки чистых активов агента x ^a во внутренних ценах (11)):

aa

Q a ( t ) = W a + —— = W a + 7 a x a . (13) ξ ^a

Капитал удовлетворяет уравнению dQa = pa(t)Qa - 9av(t),      (14)

в котором величина p a = —i a /i a 7 0 имеет смысл внутренней доходности.

Анализ выражения для балансовой прибыли pa (t)Qa (t), приведённый в [16], обнаруживает полное соответствие бухгалтерским правилами исчисления указанной величины. При этом использование в бухгалтерском учете ни от кого не полученной прибыли от переоценки и никому не заплаченных амортизационных отчислений можно интерпретировать как стремление приблизить оценку чистых активов в рыночных ценах p(t) к их «истинной» оценке во внутренних ценах (11). При нарушении однородности вследствие монопольного положения агента на рынке, наличия экономии от масштаба производства или ограничений типа квот и пр. в правой части (14) появляются дополнительные слагаемые, имеющие смысл косвенных доходов или упущенной выгоды. Интегралы от слагаемых по будущему времени, дисконтированные с показателем доходности pa (t), можно интерпретировать как объективно обусловленную денежную оценку нематериальных активов агента.

В модели равновесия с управлением капиталом величина Q a важна при описании взаимодействия фирмы и её собственника. Фирма сообщает собственнику «курс» θ ^a и прогноз доходности p a ( t ), а собственник, используя уравнение (14) как описание динамики его вложений в фирму определяет наиболее выгодную для него временную пропорцию выплаты дивидендов v ( t ), которую сообщает фирме. (Альтернативная возможность описания данного взаимодействия предложена в [18].)

Наконец, величину капитала Q a ( t ) оказалось возможным использовать для нового решения старой проблемы о терминальных условиях на конце интервала планирования [ t о ,Т ]. Мы предлагаем ставить единственное терминальное условие роста капитала Q a ( t ) в определённое число раз: Q a ( T ) = е ^{7 ( T - t} 0 ) Q a ( t о ). Разумность такой постановки задачи ¹⁵ обоснована в [25].

Вернемся к гамильтоновой системе (12). Бесчисленные нейтрально устойчивые колебания и вращения в физике получаются потому, что в физических приложениях функция Гамильтона чаще всего выпукла вверх, и устойчивые особые точки системы (12) суть центры вокруг минимумов энергии. Но при характерных для экономики целях максимизации капитализации, полезности, прибыли и т. п. функция Гамильтона получается выпуклой вниз по «импульсам» λ и выпуклой вверх (вогнутой) по «координатам» q. В результате типичными особыми точками оказываются седла, а импульсы λ, в отличие от физики, оказываются ненаблюдаемыми и неустойчивыми.

Фактически динамической системы из (12) не получается: надо решать краевую задачу, определяя координаты по предыстории от начальных значений, а импульсы из будущего по прогнозу от условий трансверсальности при t = T . Таким образом, в экономических задачах импульсы А ( t ) — агрегаты информации о будущем, необходимые для принятия оптимального решения в текущий момент t . Неустойчивость динамики А ( t ) в прямом времени означает её устойчивость в обратном времени, поэтому в разумно поставленной задаче влияние деталей отдаленного будущего на текущее решение оказывается слабым. В этом состоит незнакомое физике магистральное свойство [10: Turnpike Theorem] ¹⁶ : оптимальная траектория при большом горизонте планирования «прижимается» к устойчивой сепаратрисе седла и, следовательно, слабо зависит как от начальных, так и от терминальных условий.

Самым важным и интересным из результатов наших исследований за последние 2 года стало обнаружение сильного магистрального эффекта. Во всех прикладных моделях, построенных по описанным выше принципам, при тех значениях постоянных параметров, при которых модель воспроизводит статистику, магистральный эффект проявляется столь сильно, что влияние будущего фактически полностью затухает за один шаг расчёта [26]. Это означает, что вместо динамических уравнений для импульсов в (12) можно использовать их квазистационар-ные значения, определяемые конечными соотношениями

0= ^∂H ^a ( t,q,λ ) .          (15)

∂q

С математической точки зрения поведение агента описывается динамической системой. С содержательной точки зрения, получается, что, хотя в модели рациональных ожиданий мы разрешаем агенту знать будущее, институциональные ограничения при правильных значениях параметров так «зажимают» его возможности, что для выработки оптимального решения оказывается достаточным знания текущей конъюнктуры! Впрочем, ставить задачу (6) –(9) и выводить для неё условия оптимальности все равно нужно, поскольку без этого угадать конкретный вид соотношений (15) невозможно.

• IV. Модель экономики России периода кризиса

• IV .1. Опыт разработки моделей МРК

Если объединить условия оптимальности всех макроагентов (блоки ЭА на рис. 2) со сценарным описанием действий индивидуальных агентов и дополнить их описаниями взаимодействий (блоки ВД на рис. 2), содержащими прежде всего балансы финансовых и материальных потоков между агентами, а также некоторые потоки информации, то получится макромодель межвременного равновесия с управлением капиталом (МРК), которую мы в настоящее время изучаем и используем. Специфика изучаемой экономики выражается, во-первых, набором агрегированных аддитивных величин (материальных и финансовых активов), на их языке описываются поведение и взаимодействие агентов, и, во-вторых, набором и формой институциональных ограничений. Набор агентов почти однозначно определяется системой балансов выбранных аддитивных ве-личин ¹⁷ ).

Реалистичная модель такого типа сводится к краевой задаче, которая исходно содержит около сотни соотношений, включающих, кроме конечных и дифференциальных уравнений, ещё и условия дополни-тельности ¹⁸ . Поэтому для расчётов по модели МРК приходится использовать весьма замысловатые алгоритмы [16]. В то же время настроечных параметров в модели оказывается немного: 2–3 десятка против сотен в эконометрических, имитационных или CGE макромоделях. Когда модель МРК плохо воспроизводит статистику, приходится изменять форму исходных соотношений и делать заново все выкладки.

Проделать такую работу, записывая модель на бумаге и переводя запись на язык программирования, за разумное время без ошибок и искажения исходных предположений абсолютно невозможно. Эффективно работать с моделью МРК удаётся только благодаря использованию интеллектуальной системы поддержки математического моделирования ЭКОМОД, реализованной в среде компьютерной алгебры Maple. ЭКОМОД проверяет корректность модели, позволяет автоматически повторить выкладки при изменении исходных уравнений, реализует алгоритм расчётов непосредственно для формульной записи системы соотношений модели и на всех этапах записывает модель в виде, пригодном для публикации.

Первая модель МРК, описывавшая развитие экономики России, была построена нами по заказу налогового ведомства в 2003–2004 гг. для решения задачи по оценке размеров теневого оборота и налогового потенциала по данным внешним по отношению к налоговому ведомству. Эта модель детально описана в [16]. В 2006 г. она была модифицирована. Модифицированная модель правильно и по времени, и по объёму описала переход от вывоза к ввозу капитала в России в 2006 г. При этом надо учесть, что модель ничего «не знала» об организации в тот период госкорпораций, внешние займы которых реализовали основной объём ввоза капитала. Результат показал, что модели МРК способны описывать перелом тенденций, что дало надежду успешно использовать их в период кризиса.

Однако уже в начале 2008 г. выявились расхождения расчётов и статистики. Они были в первую очередь связаны с тем, что динамика индексов цен отдельных составляющих основного макроэкономического баланса (3) в России стала сильно различаться, а в модели для всех составляющих постулировался единый индекс цен. По этой причине мы начали исследования по переработке модели. В настоящее время они проводятся по заказу ЦБ РФ в рамках задачи по оценке сравнительной эффективности различных способов организации системы денежного обращения в российских условиях. Работа проводится нашим коллективом из ВЦ РАН под руководством акад. А.А. Петрова (чл.-корр. РАН И.Г. Поспелов, к.ф.-м.н. М.Ю. Андреев, к.ф.-м.н. И.И. Поспелова, к.ф.-м.н. М.А. Хохлов, инж.-мат. Н.К. Бурова, аспирант ВМК МГУ В.П. Вржещ, аспирантка МФТИ А.А. Жукова, аспирант ВШЭ Н.П. Пильник) совместно с коллективами из ЦЭМИ РАН (руководитель — акад. В.Л. Макаров) и Института новой экономики ГАУ (руководитель — акад. С.Ю. Глазьев). Модель ещё не закончена, и ниже приведены только самые первые предварительные результаты.

Параллельно нами проводится также разработка модели МРК для Казахстана по заказу Национальной академии наук Республики Казахстан, и сейчас появились первые обнадеживающие результаты.

• IV.2. Предварительные результаты моделирования развития экономики

России в период кризиса

В последней модели экономики России описываются реальный сектор, производящий внутренний и экспортный продукты и потребляющий внутренний и импортный продукты, и финансовый сектор. Сопровождающие производство, распределение и потребление продуктов финансовые потоки описываются как оборот 6-ти финансовых инструментов: наличных денег, остатков расчётных счетов, остатков корреспондентских счетов в ЦБ, банковских ссуд, банковских депозитов, депози-тов/кредитов банков в ЦБ, иностранной валюты.

Продукты, труд и финансовые инструменты образуют набор аддитивных величин, для которых в модели выписывается полная система балансов, причём потоки финансовых инструментов разделяются на легальные и теневые.

Развитие экономики, выраженное движением аддитивных величин, описывается как результат деятельности 9 макроагентов:

• 1)    производителя, представляющего совокупность нефинансовых коммерческих организаций;

• 2)    банка, представляющего совокупность финансовых коммерческих организаций;

• 3)    населения, представляющего физических лиц — потребителей и наемных работников;

• 4)    собственника, представляющего физических и юридических лиц, управляющих движением капитала между секторами национальной экономики и за пределы страны;

• 5)    торговца как чистого посредника между потребителями, производителем, экспортером и импортером;

• 6)    государства, деятельность которого представлена в модели явно агрегированным описанием деятельности Министерства финансов и неявно — установлением различных параметров экономической политики (ставок налогов, госрасходов, норм резервов и др.);

• 7)    центрального банка, представленного в модели своими функциями эмитента национальной валюты, держателя валютных резервов, расчётного центра и кредитора коммерческих банков;

• 8)    экспортера;

• 9)    импортера.

Общая схема модели и описание большинства блоков остаются теми же, что в [16], поэтому остановимся только на отличиях.

— Был существенно переработан и отдельно детально исследован блок «Банк» [26]. На этом примере детально исследован сильный магистральный эффект, проявляющийся и во всей модели в целом.

— Наиболее важным и технически сложным изменением стал переход от однопродуктовой модели, описывающей все материальные потоки как части реального ВВП, к трёхпродуктовой модели, в которой составляющие реального макроэкономического баланса выражаются как разные нелинейные свёртки трёх продуктов: внутреннего (включая услуги), экспортного и импортного. Ввиду редкости поступления и неполной адекватности в настоящих условиях статистических данных по межотраслевому балансу мы не стали, как обычно принято, получать трёхпродуктовое описание агрегированием отраслевых показателей, а пошли путём дезагрегирования основного макроэкономического баланса, используя упомянутое различие индексов цен отдельных составляющих баланса. В модели эта операция несколько условно передана агенту «Торговец». Торговец расщепляет (нелинейно) продукт производителя (реальный ВВП) на внутренний и экспортный продукты, а затем комбинирует (опять-таки нелинейно) потребительский и инвестиционный продукты из внутреннего и импортного.

— Использование трёх продуктов позволило существенно усовершенствовать описание внешней торговли в модели. Если в предыдущих версиях объём экспорта задавался экзогенно и его надо было прогнозировать независимо от модели, то в последнем варианте экспорт стал эндогенной величиной. Сейчас независимо от модели нужно задавать только динамику импортных и экспортных (мировых) цен, динамику расходов бюджета, политику изменения курса рубля по отношению к иностранной валюте и, как и в предыдущих версиях модели, занятость. Попытки найти адекватное описание российского рынка труда пока остались тщетными.

Результаты первых сугубо пробных расчётов для показателей реального сектора приведены на рис. 3–10. Показатели финансового сектора пока воспроизводятся хуже, и мы их не приводим. Серой линией показаны ряды несглаженных квартальных статистических данных от первого кв. 2004 г. до первого кв. 2009 г., а черной линией — расчёт с прогнозом от первого кв. 2004 г. до первого кв. 2010 г. Подчеркнем, что вся совокупность сложных траекторий

ТРУДЫ МФТИ. — 2009. — Том 1, № 4 представляет одно экономическое равновесие.

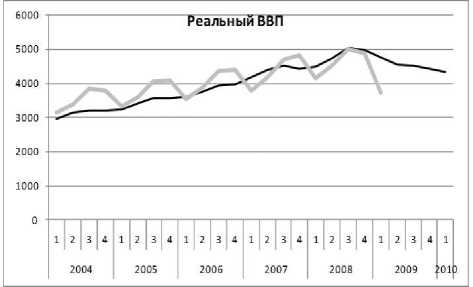
Рис. 3

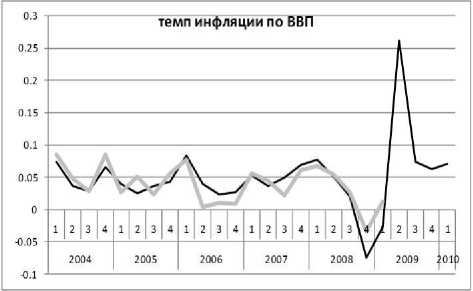
Рис. 4

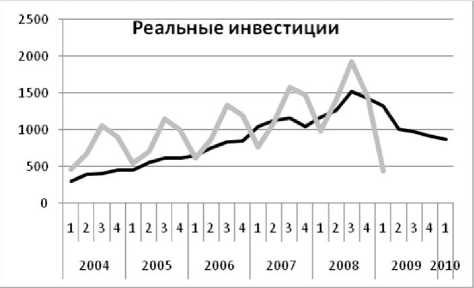
Рис. 5

Видно, что модель вполне удовлетворительно воспроизводит статистику, включая фазы колебаний и спад в результате кризиса. Она также воспроизводит различие в динамике индексов цен: дефлятора ВВП (рис. 4), индекса цен капитальных вложений (рис. 6) и индекса потребительских цен (рис. 8). Модель описывает феномен, который отличает российский кризис от кризиса во всех остальных странах: везде спад производства сопровождается дефляцией, а у нас — инфляцией! Единственный зафиксированный статистикой дефляционный процесс — падение индекса цен капитальных вложений в конце 2008 г. — модель воспроизводит.

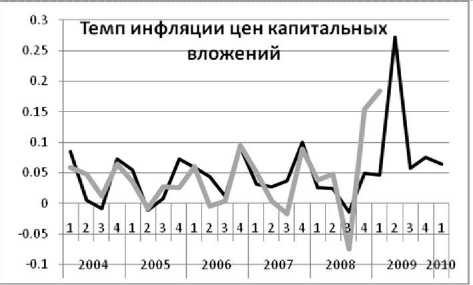
Рис. 6

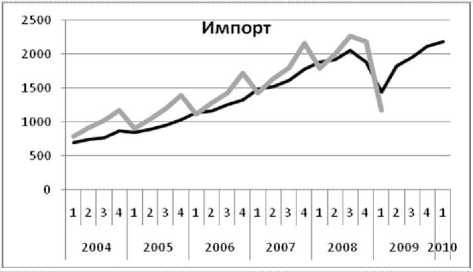
Рис. 10

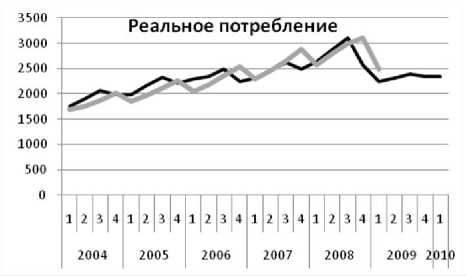
Рис. 7

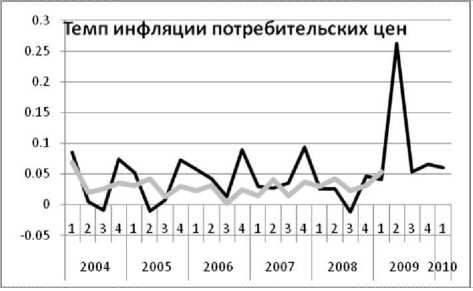
Рис. 8

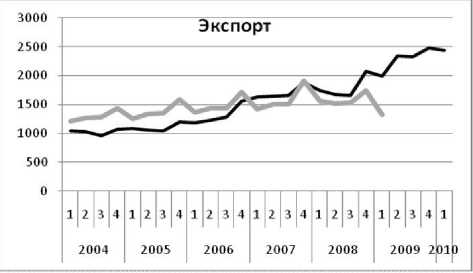
Рис. 9

V. Заключение: антропный экономический принцип

С практической точки зрения главным результатом наших последних исследований стало то, что модели МРК оказались способными воспроизводить кризисные явления в экономике.

С научной точки зрения главным результатом, полученным за последние два года, стало обнаружение сильного магистрального свойства. Напомним, в чем оно состоит: хотя в модели мы разрешаем агентам знать будущее, это знание оказывается им не нужным при выработке оптимального поведения. Постольку поскольку свойство выполняется, оно снимает все возражения против применения принципа рациональных ожиданий. Последний оказывается нужным только для нахождения соответствующей исследуемой экономической системе формы конечных уравнений (15). Затем модель сводится к традиционной динамической системе ¹⁹ . Но феномен сильного магистрального свойства сам нуждается в объяснении.

Ключом здесь служит то, что сильный магистральный эффект проявляется в модели не вообще, на уровне формул, а только при правильно идентифицированных значениях параметров [26]. Тут надо вспомнить, что экономика как управляющая система должна не просто скоординировать действия миллиардов людей, но сделать это так, чтобы люди в большинстве случаев могли делать разумный выбор без сложных расчётов. Поэтому даже известные всем экономические механизмы могут не работать из-за своей сложности

и риска. Например, в России все с 1994 г. знали, что можно брать потребительские кредиты в банке, но почти не просили, а банки почти не давали. К 2003 г. кредитноденежная система и доходы стабилизировались, потребительское кредитование перестало требовать детальных расчётов и строгих гарантий и стало расти лавинообразно.

Обобщая пример, можно предположить, что в каждый момент времени в экономике отбирается и действует такой комплекс механизмов, который не требует детальных расчётов для разумных решений. Поэтому описывая в модели механизмы «по жизни», а не по учебникам, мы получаем модель с сильным магистральным свойством.

Все это несколько напоминает известный в физике антропный принцип [27]: Вселенная представляется наблюдателю гармоничной и «приспособленной» к нему потому, что во Вселенной с иным устройством наблюдатель не возникнет.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (код проекта 07-01-00563-а), Российского гуманитарного научного фонда (код проекта 07-02-00362), по программе государственной поддержки ведущих научных школ (код проекта НШ-2982.2008.1), программ фундаментальных исследований ОМН РАН № 3 и ПФИ Президиум РАН П-2.