Равновесные системы "газ-жидкость" для сплава Sn-Sb при вакуумной дистилляции
Автор: Королев А.А., Краюхин С.А., Мальцев Г.И.
Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu
Статья в выпуске: 4 т.12, 2019 года.
Бесплатный доступ
При переработке чернового свинца необходимо отделить металл от примесей - меди, олова, сурьмы, мышьяка, серебра, висмута с возможным использованием экологически безопасной, технологически эффективной и экономически выгодной высокопроизводительной вакуумной дистилляции. Для анализа поведения поликомпонентного сплава в процессе переработки, предварительного выбора температуры и давления системы, оценки эффективности разделения компонентов при вакуумной перегонке используют фазовые диаграммы температура-состав «Т-х» и давление-состав «Р-х». Цель работы состояла в расчете равновесных состояний «газ-жидкость» VLE (vapor liquid equilibrium), включая зависимости состава фаз от температуры (Т-х) и давления (Р-х) для Sn-Sb-сплава при вакуумной перегонке на основе объемной модели молекулярного взаимодействия MIVM (мolecular interaction volume model), а также определение термодинамических параметров процесса. В интервале температур 823-1073 К рассчитаны давления насыщенного пара (Па) для Sn (3,32.10-9-8,12.10-5) и Sb (3,954-273,66)...
Газ, жидкость, равновесие, диаграмма, модель, вакуум, сплав, температура, дистилляция, олово, сурьма, разделение, мольная доля, энергия гиббса
Короткий адрес: https://sciup.org/146281213
IDR: 146281213 | УДК: 669.6.8...471:669.053:66.048.1-982 | DOI: 10.17516/1999-494X-0151
Текст научной статьи Равновесные системы "газ-жидкость" для сплава Sn-Sb при вакуумной дистилляции
модействия ( мolecular interaction volume model – MIVM ). Объективные VLE зависимости важны для выбора температуры и давления системы, оценки эффективности разделения в вакуумной перегонке. Определение термодинамических характеристик из экспериментальных данных занимает много времени и требует значительных финансовых затрат. Следовательно, теоретический расчет является альтернативным и эффективным способом получения информации о термодинамических свойствах сплавов, особенно для многокомпонентных систем [5–8]. С использованием названных моделей можно оценить термодинамические параметры процесса взаимодействия компонентов сплава в жидкой фазе.
Методика исследований
В равновесной системе «жидкость–газ» химический потенциал (фугитивность) каждого компонента в обеих фазах одинаков и соответствует зависимости [9]
Ф"" . ...
где Фi - фугитивность компонента i в газовой фазе; Ф* - коэффициент фугитивности насыщенной жидкости чистого компонента i ; T ир - температура и давление в системе; р* i - давление насыщенных паров чистого компонента i при температуре T; Y i - коэффициент активности компонента i в жидкой фазе при данных температуре, давлении и мольной доли компонента i ; х i и уi – мольная доля компонента i в жидкой и газовой фазах соответственно; Vli – мольный объем чистой жидкости i ; R – универсальная газовая постоянная.
Остаточное давление в исследуемой системе достаточно низкое (р ≤ 133 П ведет себя как идеальный газ, откуда Ф, = Ф*- 1,0, а экспоненциальный член ехр (^^) « 1.
Таким образом, уравнение ( 1 ) можно упростить, подобно модифицированному закону Рауля [9]:
pyt = PiYixi.
Если жидкая смесь является идеальным раствором, то γ i = 1 в (2). ■
Для бинарного сплав а i- j справедливо:
x i + x = 1, y i + y j = 1,
P = PlYtXt + PjYjXj = PlYtXt + PjYj(l — xt).
Объединяя уравнения J 2) и (4), получим выражения для х, и у ,:
х,=^,
,«-„, ,
У1=!^.
Коэффициенты активности компонентов в жидкой фазе имеют решающее значение для расчета фазовой диаграммы VLE. Модель MIVM [10] считается одной из наиболее удобных и надежных [11-13]. Согласно MIVM, молярная избыточная энергия Гиббса Gh для границы раз-
■ ■ i- дел а фаз «жидкоси, !аз» смеси i -j может быть выражена как
V
^ = хап
____Vm____
.X^mi + X jVmj B j L
+ %7ln ——
J J \X j V mj
Vmj
+ xiVmiBij
)
X ( X j Z i B jt lnB jt Z jBtjlBBtk
2 ( xt+X j B j i X j — x ^ B j ) ,
где x i и xJ - молярныie доли; Z i и Z - координационные числа; Vmi и VmJ молярные объемы компо-ненто в i и j с о ответственно; R - универсальная газовая постоянная, а потенциальные энергии парного взаимодействия Ву и Byi определяются следующим образом:
с • .__с -- с ____с ••
Bij = ехр [ - (^)] Bii = ехр -Лг^
где k - константа Больцмана; Е , Еи и Ejj - потенциальные энергии парного взаимодействия i-J, i-i , j-j систем, где e j - j
Для бинарной смеси i-j, с помощью термодинамического соотношения ( d G E m/ d x i ) T,p,X j , коэффициенты активности компонентов i и j могут быть получены из у равнения (7 ) , с оответственно, как
Н = ln I ■
1 V
■ v m, i
x tV m .i + X jV^j B jy
j " (
- B --v m,j j ji
V m,i B ij
, XiVm,i + XjVm,jBji. XjVm,j + XiV m ,iBij
x2 [ [ XtBX i l BBjl + Z j B X j i BBjj ] 2 (x 1+ x jBj i^^ (X j +xtU y V ’
)
/ hr/ ■ = 1П I "
Vm , j
. xj VmJ + ^Aj
) + (
'Vm,iBij
.x jVm,j + ,ciBjm,iBij
Vm,jBji xi V m,i m xj V m,j B j t
^ Jv z jB>B lj + z^ y ] . 2 (X j- VX i B ij Y (X i +X j B jj)2
)-
) (10)
Когда x, или x, в приближаются к нулю, коэффициенты активности бесконечно разбавлен-i J г B в ных растворов у” и у” являются произ водными из уравнений (9) и (10) следующим образом:
lnej = 1 - ln ('; " ) -v^ - -2(ZilnI3ji + ZjVijlnVij),(11)
jv2iiuz V^j-ji1
Yj I vmj ) VmJ z( X'ln lX + 1 Xl^U Xl)( )
Необходимые двоичные параметры Bij и Bji можно рассчитать из уравнений (11) и (12)
Л. . ■„, J A.J по формуле Newton [10] если известны коэффициенты активности для бесконечно разбавленных растворов, т. е. у” и yj° бинарных жидких сплавов и свответствующие параметры их компонентов [14, 15]. Координационное число Zi жидких металлов рассчитывают как [10]:
Z t =
^^^^ ( j ^ E^ 21) Pi Tmi exip(-
5 vrmi ' oi7
. AHm i (Tm i Т)
ZcRTTmi
где pi = Ni/V, - молекулярная плотность; V - мольный объем и N - число молекул, AHmi - энтальпия плавления; T. - температура плавления; Z, = 12 - коорлипациоиное число плотной – 491 – упаковки, Т – температура жидкого металла, K; R – газовая постоянная; r0i = 0,918dcovi – доля атомного ковалентного диаметра (dcovi), который подразумевает, что длина ковалентной связи образуется путем обмена внешних валентных электронов с другими атомами элемента при подходе на наименьшее расстояние между соседними атомами; rmi равняется, примерно, атомному диаметру σi, (rmi = σi).
Значения B и B при требуемой температуре (Т ) можно получить из уравнения (8) для jj известных значений B и B при температуре (Т ), принимая независимой от температуры по-ij ji 1
Et j -E jj E ji —E tt.
тенциальную энергию парного взаимодействия компонентов--^^-^ и — —. Например, в бинарной системе S b / 1 1 /1
сс
-^= , ,„»,= ^U095 ) = 4 K;
ВО = exp (НМ/ 973 ) = 1,101; Цвц - s„ ) = -ОДОМ э-в;
TT::"TK;
exp^fiS^Wl; (,„ «„ >e,«”“’B
Давление насыщенных паров чистых компонентов рассчитывают [16] таким образом:
lgp = AT + BlgT + CT + D , (14)
где p* – давление насыщенных паров чистого компонента, Па; А, B, C, D – константы испарения для компонентов жидких сплавов, Т – абсолютная температура.
Необходимые для расчета параметрыSn-Sb-сплава даны в табл. 1.
Для выполнения экспериментальных исследований на лабораторной установке вакуумной возгонки были приготовлены Pb-Sb-сплавы с переменным содержанием компонентов в диапазоне 0,1–0,9 мольных долей ( хij ). Степень разряжения в вакуумной камере во время эксперимента составляла 1,3–133 Па, температура 823–1073 К , продолжительность (до момента установления равновесия в системе) 2–10 ч. Образцы возгонов и жидкой фазы были получены из конденсата и огарка (остатка) соответственно. Анализ на содержание свинца и сурьмы в продуктах дистилляции выполнен из предварительно полученных растворов атомно-абсорбционным методом на установке GBC 933 АВ Plus .
Таблица 1. Значения уГ , ,Т , В. , Bj, Zt, Z, р ^ , р ^ , V m (, ) сплава Sn-Sb Table 1. Values у ? , у ” , Btj , Bjt, Zt, Zj, р * , р^, V m уа) alloy Sn-Sb
|
i–j сплав |
Т, К |
∞ P Sn |
∞ Y sb |
B Sn – Sb |
B Sb – Sn |
Z Sn |
Z Sb |
|
Sn-Sb |
905 |
0,411 |
0,411 |
1,1095 |
1,0937 |
6,5512 |
6,9698 |
|
Компонент |
А |
В |
С |
D |
V m |
= f ( T ) , см3/моль |
|
|
Sn |
–15500 |
0 |
0 |
10,355 |
17 0[1 |
+ 0,87.10–4(T–505)] |
|
|
Sb |
–6500 |
0 |
0 |
8,495 |
18,8[1 + 1,3.10–4(T–904)] |
||
Для того чтобы проверить адекватность расчетных значений содержания компонентов PbSb-сплава в жидкой и газовой фазах, сравнили их с экспериментальными данными. Для этого были вычислены показания среднего относительного отклонения ( Si ) и среднего квадратичного отклонения ( S t ):
S - = ±vS-i |
I х ( у ) i £ xp х ( у )i,cal I х ( у ) isxp
I•100 %,
S t = ± [ ^ E "=1 [ х ( у Xexp - х ( у ) i,caz ] 2 ] ,
где x ( y ) i , exp и x ( y ) i , cal – экспериментальные и расчетные значения содержания компонента i в жидкой и газовой фазах соответственно; n – количество экспериментальных данных.
Обсуждение результатов
Сурьма имеет высокое давление насыщенных паров и легко испаряется в газовую фазу, олово имеет низкое давление насыщенных паров и остается в жидкой фазе, что предполагает возможность разделения этих металлов вакуумной дистилляцией (табл. 2).
Для оценки возможности разделения элементов i и j бинарного сплава i–j вакуумной дистилляцией используем рассчитанные коэффициенты активности (табл. 3) и коэффициент разделения β i :
о _ Psb Y sb P sb = TT—.
P sn Y Sn
Значения β Sb > 1 (рис. 1, табл. 4), поскольку cодержание cурьмы в газовой фазе больше, чем в жидкой ( у Sb >> x Sb). Сурьма обогащает газовую фазу, а олово накапливается в жидкой фазе Sb Sb
( x Sn >> у Sn ), таким образом, бинарный сплав разделяется на сурьму и свинец.
Коэффициент разделения cурьмы и олова возрастает ( log βSb = 6,262–9,435) по мере снижения температуры процесса (1073–823 К ) и доли олова ( x = 0,9–0,1) в составе бинарного Sn-Sb-сплава. Для Sn–Sb-сплава, с учетом равенства (3), содержание металлов в газовой фазе таково:
yS n = [i+ ™b ; sb ] " , ysb = [i+ L P sn / sn ^ snj L
P Sn Y Sn X Sn P sb / Sb ^ Sb.
г
.
Таблица 2. Рассчитанные давление и соотношение давления паров Sb и Sn
Table 2. The calculated pressure values and the pressure ratio Sb and Sn vapor
|
Т , К |
р* Sb , Па |
р* Sn , Па |
( р * Sb / р * Sn ) .103 |
|
823 |
3,95 |
3,32.10–9 |
1,19.109 |
|
873 |
11,205 |
3,98.10–8 |
2,81.108 |
|
923 |
28,363 |
3,65.10–7 |
7,678.107 |
|
973 |
65,257 |
2,66.10–6 |
2,45.107 |
|
1023 |
138,401 |
1,60.10–5 |
8,66.106 |
|
1073 |
273,664 |
8,12.10–5 |
3,37.106 |
Таблица 3. Рассчитанные значения коэффициентов активности Sn и Sb в расплаве
Table 3. The calculated values of the activity coefficients of Sn and Sb in the melt
|
Т, К |
γ |
x Sn |
||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
||
|
823 |
γ Sn |
0,433 |
0,517 |
0,604 |
0,691 |
0,774 |
0,849 |
0,912 |
0,960 |
0,990 |
|
γ Sb |
0,990 |
0,960 |
0,913 |
0,850 |
0,776 |
0,694 |
0,609 |
0,523 |
0,439 |
|
|
873 |
γ Sn |
0,456 |
0,539 |
0,623 |
0,707 |
0,786 |
0,857 |
0,917 |
0,962 |
0,990 |
|
γ Sb |
0,990 |
0,963 |
0,918 |
0,859 |
0,788 |
0,710 |
0,627 |
0,544 |
0,462 |
|
|
923 |
γ Sn |
0,478 |
0,559 |
0,641 |
0,721 |
0,797 |
0,865 |
0,921 |
0,964 |
0.991 |
|
γ Sb |
0,991 |
0,965 |
0,922 |
0,866 |
0,799 |
0,724 |
0,645 |
0,563 |
0,483 |
|
|
973 |
γ Sn |
0.498 |
0,577 |
0,657 |
0,734 |
0,807 |
0,872 |
0,926 |
0,966 |
0,991 |
|
γ Sb |
0,992 |
0,967 |
0,927 |
0,873 |
0,809 |
0,737 |
0,660 |
0,581 |
0,502 |
|
|
1023 |
γ Sn |
0,517 |
0,594 |
0,671 |
0,746 |
0,816 |
0,878 |
0,929 |
0,968 |
0,992 |
|
γ Sb |
0,992 |
0,968 |
0,930 |
0,880 |
0,818 |
0,749 |
0,675 |
0,598 |
0,521 |
|
|
1073 |
γ Sn |
0,534 |
0,610 |
0,685 |
0,757 |
0,824 |
0,883 |
0,933 |
0,969 |
0,992 |
|
γ Sb |
0,992 |
0,970 |
0,934 |
0,885 |
0,826 |
0,760 |
0,688 |
0,613 |
0,538 |
|
Таблица 4. Рассчитанные значения коэффициента разделения cурьмы и олова ( log βSb)
Table 4. The calculated values of partition coefficient antimony and tin ( log βSb)
|
x Sn |
823 К |
873 К |
923 К |
973 К |
1023 К |
1073 К |
|
0,1 |
9,435 |
8,786 |
8,207 |
7,689 |
7,221 |
6,797 |
|
0,2 |
9,344 |
8,701 |
8,128 |
7,614 |
7,150 |
6,729 |
|
0,3 |
9,255 |
8,618 |
8,049 |
7,539 |
7,079 |
6,662 |
|
0,4 |
9,166 |
8,534 |
7,970 |
7,465 |
7,009 |
6,596 |
|
0,5 |
9,077 |
8,450 |
7,892 |
7,391 |
6,939 |
6,529 |
|
0,6 |
8,988 |
8,368 |
7,814 |
7,317 |
6,869 |
6,463 |
|
0,7 |
8,900 |
8,284 |
7,736 |
7,243 |
6,799 |
6,395 |
|
0,8 |
8,812 |
8,202 |
7,657 |
7,169 |
6,728 |
6,329 |
|
0,9 |
8,722 |
8,118 |
7,579 |
7,094 |
6,658 |
6,262 |
Зависимость количества олова в газовой фазе у Sn от содержания олова в расплаве x Sn = 0,1–0,9 и температуры процесса Т = 823–1073 К представлена на рис. 2 и в табл. 5. В области малых концентраций олова ( x Sn = 0,001–0,05) в Sn-Sb-сплаве соответствующие значения коэффициентов активности компонентов и содержание олова в газовой фазе у Sn даны в табл. 6, 7 и на рис. 3.
О чистоте отогнанной сурьмы можно судить по выявленным зависимостям «y –x » при заданном температурном режиме (рис. 2, 3). Сурьма может быть отделена от олова при температуре возгонки свыше 550 °С. При известном исходном количестве олова в сплаве можно подобрать температуру процесса, обеспечивающую заданную остаточную концентрацию примеси в рафинированной сурьме. Например, исходное значение x (ат. % / мас. %) = 4,0/3,9; тогда при 600 °С уSn (ат. % / мас. %) = 1,0.10–10/ 0,975.10–10, а при 800 °С уSn (ат. % / мас. %) = 61.10–10/59,47.10–10, т.е. содер- log βSb
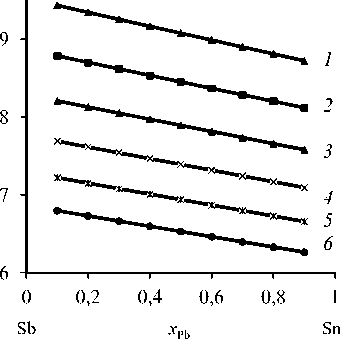
Рис. 1. Коэффициент разделения сурьмы при вакуумной дистилляции Sn-Sb-сплава при температуре, К : 823 ( 1 ); 873 ( 2 ); 923 ( 3 ); 973 ( 4 ); 1023 ( 5 ); 1073 ( 6 )
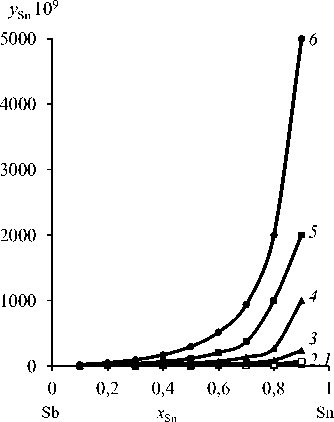
Рис. 2. Зависимость « y Sn– x Sn» Sn-Sb сплава при температуре, К : 823 ( 1 ); 873 ( 2 ); 923 ( 3 ); 973 ( 4 ); 1023 ( 5 ); 1073 ( 6 )
-
Fig.1. Partition coefficient antimony vacuum distillation Sn-Sb alloy at a temperature, К : 823 ( 1 ); 873 ( 2 ); 923 ( 3 ); 973 ( 4 ); 1023 ( 5 ); 1073 ( 6 )
-
Fig.2. Dependence “ y Sn – x Sn ” Sn-Sb alloy at a temperature, К : 823 ( 1 ); 873 ( 2 ); 923 ( 3 ); 973 ( 4 ); 1023 ( 5 ); 1073 ( 6 )
Таблица 5. Рассчитанные значения у Sn .10–9 сплавa Sn-Sb
Table 5. Calculated values у Sn.10–9 alloy Sn-Sb
Рассчитанные значения коэффициентов активности компонентов сплава Sn-Sb (табл. 4) позволили определить активности олова и сурьмы в расплаве (рис. 4) [17, 18].
Для построения « Т-х »-диаграммы бинарной системы i–j используют интерактивный алгоритм различных значений хi для определенной температуры до тех пор, пока сумма парциальных давлений становится равной внешнему давлению [19–24]. Подставляя соответствующие величины γ , γ , p , p * и p * при различных температурах (табл. 8, 9) в уравнения (3), (5) и (6), получаем « Т-х »-фазовую диаграмму сплава Sn-Sb (рис. 5).
Таблица 6. Рассчитанные коэффициенты активности Sn-Sb-сплавa
Table 6. The calculated activity coefficients alloy Sn-Sb
|
T , K |
x Sn |
||||||||
|
γ |
0,001 |
0,003 |
0,005 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
|
|
823 |
γ Sn |
0,355 |
0,357 |
0,358 |
0,362 |
0,370 |
0,377 |
0,385 |
0,393 |
|
γ Sb |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
0,999 |
0,999 |
0,998 |
|
|
873 |
γ Sn |
0,379 |
0,381 |
0,382 |
0,386 |
0,394 |
0,401 |
0,409 |
0,417 |
|
γ Sb |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
0,999 |
0,999 |
0,998 |
|
|
923 |
γ Sn |
0,402 |
0,403 |
0,405 |
0,409 |
0,416 |
0,424 |
0,431 |
0,439 |
|
γ Sb |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
0,999 |
0,999 |
0,998 |
|
|
973 |
γ Sn |
0,423 |
0,425 |
0,426 |
0,430 |
0,437 |
0,445 |
0,452 |
0,460 |
|
γ Sb |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
0,999 |
0,999 |
0,998 |
|
|
1023 |
γ Sn |
0,443 |
0,444 |
0,446 |
0,450 |
0,457 |
0,464 |
0,472 |
0,479 |
|
γ Sb |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
0,999 |
0,999 |
0,998 |
|
|
1073 |
γ Sn |
0,462 |
0,463 |
0,464 |
0,468 |
0,475 |
0,483 |
0,490 |
0,497 |
|
γ Sb |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
0,999 |
0,999 |
0,998 |
|
Таблица 7. Рассчитанные значения y Sn.10–10 Sn-Sb-сплавa
Table 7. Calculated values y Sn.10–10 alloy Sn-Sb
|
x Sn |
823 |
873 |
923 |
973 |
1023 |
1073 |
|
0,001 |
< 1 |
1 |
1 |
|||
|
0,003 |
< 1 |
1 |
2 |
4 |
||
|
0,005 |
1 |
3 |
7 |
|||
|
< 0,1 |
< 1 |
|||||
|
0,01 |
1 |
2 |
5 |
14 |
||
|
0,02 |
1 |
4 |
11 |
29 |
||
|
0,03 |
2 |
6 |
17 |
44 |
||
|
0,04 |
0,15 |
1 |
2 |
8 |
23 |
61 |
|
0,05 |
0,2 |
1 |
3 |
10 |
29 |
78 |
Таблица 8. Рассчитанные значения γ Sn , γ Sb , T liq Sn-Sb-сплавa для « Т-х» -диаграмм
Table 8. Calculated values γSn, γSb, Tliq alloy Sn-Sb for “T-x” diagrams
|
P , Па |
x Sn |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
Т liq , К |
1028,2 |
1038,3 |
1050,9 |
1066,4 |
1085,5 |
1109,6 |
1141,2 |
1185,8 |
1263,8 |
|
|
133 |
γ Sn |
0,519 |
0,599 |
0,679 |
0,756 |
0,826 |
0,887 |
0,937 |
0,973 |
0,993 |
|
γ Sb |
0,992 |
0,969 |
0,932 |
0,884 |
0,828 |
0,767 |
0,704 |
0,645 |
0,592 |
|
|
Т liq , К |
887,9 |
895,6 |
905,3 |
918,9 |
932,1 |
950,7 |
974,8 |
1008.5 |
1065,6 |
|
|
13,3 |
γ Sn |
0,463 |
0,549 |
0,636 |
0,720 |
0,799 |
0,869 |
0,926 |
0,967 |
0,992 |
|
γ Sb |
0,991 |
0,964 |
0,921 |
0,841 |
0,801 |
0,732 |
0,661 |
0,593 |
0,536 |
|
|
Т liq , К |
781,2 |
787,4 |
795,2 |
804,8 |
816,9 |
831,6 |
850,8 |
877,3 |
921,4 |
|
|
1,33 |
γ Sn |
0,411 |
0,501 |
0,593 |
0,684 |
0,772 |
0,850 |
0,915 |
0,962 |
0,991 |
|
γ Sb |
0,989 |
0,958 |
0,909 |
0,847 |
0,775 |
0,698 |
0,620 |
0,547 |
0,483 |
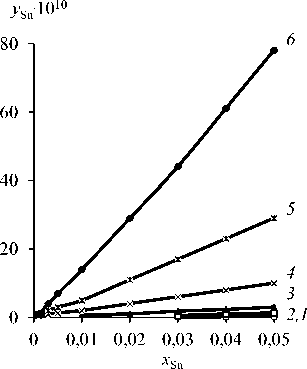
Рис. 3. Зависимость « y Sn- x Sn» Sn-Sb-сплава при температуре, К : 823 ( 1 ); 873 ( 2 ); 923 ( 3 ); 973 ( 4 ); 1023 ( 5 ); 1073 (6 )
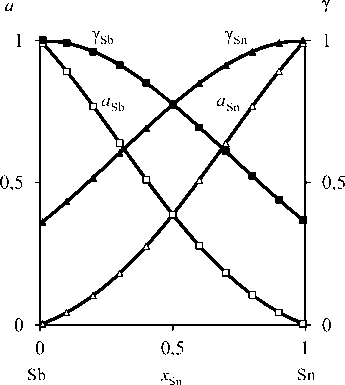
Рис. 4. Активности ( а ) и коэффициенты активности (γ) компонентов Sn-Sb-сплава при 823 К
Fig. 3. Dependence “ y Sn- x Sn” Sn-Sb alloy at a temperature, К : 823 ( 1 ); 873 ( 2 ); 923 ( 3 ); 973 (4 ); 1023 ( 5 ); 1073 ( 6 )
Fig. 4. Activities ( a ) and activity coefficients (y) components Sn-Sb alloy at 823 K
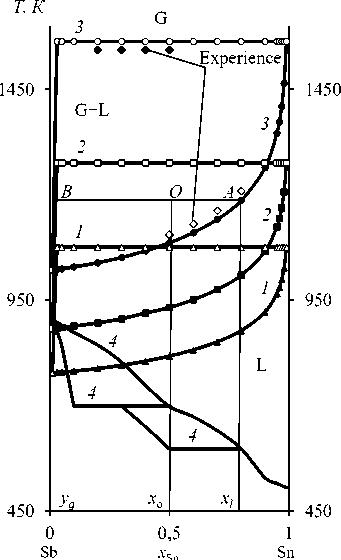
Рис. 5. Фазовые диаграммы « Т-х » при Р, Па: 1,33 ( 1 ); 13,33 ( 2 ); 133,3 ( 3 ); 98000 ( 4 )
Fig. 5. Phase Diagrams “ Т-х ” for P, Ра: 1,33 ( 1 ); 13,33 ( 2 ); 133,3 ( 3 ); 98000 ( 4 )
Таблица 9. Рассчитанные значения γSn, γSb, Tliq , у Sn Sn-Sb-сплавa для « Т-х» -диаграмм
Table 9. Calculated values γSn, γSb, Tliq , у Sn alloy Sn-Sb for “T-x” diagrams
|
P , Па |
x Sn |
0,01 |
0,90 |
0,95 |
0,96 |
0,97 |
0,98 |
0,99 |
|
Т liq , К |
1021 |
1263,8 |
1345,2 |
1372,6 |
1409 |
1464 |
1563 |
|
|
133 |
γ Sn |
0,449 |
0,993 |
0,998 |
0,999 |
0,999 |
1,0 |
1,0 |
|
γ Sb |
1,0 |
0,592 |
0,578 |
0,578 |
0,581 |
0,586 |
0,601 |
|
|
у Sn .10–4 |
~0 |
0,83 |
4,85 |
8,33 |
16,47 |
43,15 |
204,2 |
|
|
Т liq , К |
882,4 |
1065,6 |
1123,9 |
1143,2 |
1168,9 |
1206,2 |
1275,3 |
|
|
13,3 |
γ Sn |
0,390 |
0,992 |
0,998 |
0,999 |
0,999 |
1,0 |
1,0 |
|
γ Sb |
1,0 |
0,536 |
0,517 |
0,516 |
0,516 |
0,521 |
0,531 |
|
|
у Sn .10–4 |
~0 |
0,04 |
0,26 |
0,45 |
0,91 |
2,36 |
11,82 |
|
|
Тliq , К |
776,9 |
921,4 |
965,3 |
979,6 |
999,2 |
1025,9 |
1075,3 |
|
|
1,33 |
γ Sn |
0,339 |
0,991 |
0,998 |
0,999 |
0,999 |
1,0 |
1,0 |
|
γ Sb |
1,0 |
0,483 |
0,461 |
0,460 |
0,454 |
0,461 |
0,472 |
|
|
у Sn .10–4 |
~0 |
0,002 |
0,014 |
0,025 |
0,051 |
0,13 |
0,65 |
Из рис. 5 следует, что диапазон температур жидкой и газовой фаз уменьшается по мере снижения давления в системе, что указывает на благоприятное влияние низкого давления на разделение Sb и Sn. Например, для получения конденсата сурьмы (Sb ≈ 0,99) и, соответственно, остатка олова (Sn ≈ 0,99) при Р = 13,3 Па температура процесса дистилляции не должна превышать ~1275 К . Неизменное содержание олова (Sn ≈ 0,99), остающегося в жидкой фазе, при уменьшении давления Р = 133–1,33 Па достигается при меньшей температуре возгонки сурьмы – Т = 1563–1075 К .
С помощью « Т-х »-фазовых диаграмм можно анализировать протекание дистилляции, например, при Р = 133,3/13,3/1,33 Па для сплавов с x Sn = 0,01–0,99 минимальная температура процесса должна быть не ниже 1021/882/777 К . По формулам (15) и (16) вычислены средние отклонения: относительное ( S i = 1,6 %) и квадратичное ( 5t * = 7,9 К ), между рассчитанными и экспериментальными значениями температур возгонки сурьмы.
Для фазовых диаграмм VLE может быть использовано правило рычага (правило отрезков) для прогнозирования количества вещества, остатков и возгонов при заданной температуре. Предполагая, что мольная доля Sn в сырье сплава х о = 0,5, соответствующая температура перегонки ~1185 К и давление 133 Па, по правилу «рычага» может быть построена линии связи АВ на « Т-х »-диаграмме (рис. 5), где кривые жидкости и пара пересекаются в точке А и В соответственно. Когда система достигает равновесия, составы А и В равняются хl и yg соответственно. По правилу рычага можно получить:
пг _ хо-^ д _ |0В| = 0,5-0,000365 = 0,499635
nq Хх-Хр |ОЛ| 0,8-0,5 0,3 , где nl = 0,499635 и ng = 0,3 – количество вещества в остатках и возгонах; |OB| и |OA| длина соответствующих отрезков на линии AB. Если общее количество молей вещества исходного сплава n, то n = nl + ng:
ni =
Х0-У д |0B|
---- n = :—-n
X i —У д |ЛВ|
0,499635
0,799635
П = 0,625 П ,
ng =
x i -x0 |ML
---n = ■—-n x l -^ g |^B|
0,3 0,799635
n = 0,375 n .
Расчет диаграмм « Р-х » похож на построение « Т-х »-диаграмм (рис. 6). Значения γSn, γSb можно вычислить из уравнений (9) и (10) для серии величин х при заданной температуре системы, а давление насыщенных паров p Sn* и p Sb* рассчитывается из уравнений в табл. 1 при той же температуре. Затем определяют давление p системы, соответственно, для серий х Sn, х Sb , γSn, γSb, p Sn* и p Sb*, основанных на уравнении (4) (табл. 10), после чего получают у Sn из уравнения (6) (табл. 11) [26–29].
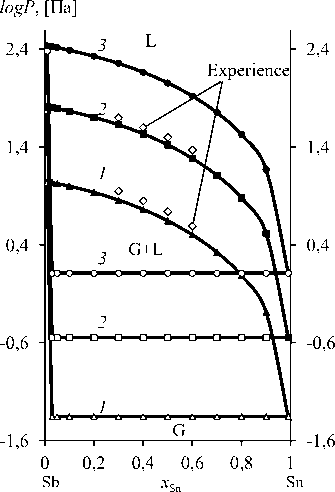
Рис. 6. Фазовые диаграммы « Р–х » при Т, К : 873 ( 1 ); 973 ( 2 ); 1073 ( 3 )
Fig. 6. Phase diagrams of the “ Р–х ” at T, К : 873 ( 1 ); 973 ( 2 ); 1073 ( 3 )
Таблица 10. Рассчитанные значения Р (Па) сплавa Sn-Sb для xl в « P-х» -диаграммах
Table 10. Calculated values Р (Ра) alloy Sn-Sb for xl in “P-x” diagrams
|
Т , К |
x Sn |
||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
|
823 |
3,52 |
3,04 |
2,53 |
2,02 |
1,53 |
1,10 |
0,72 |
0,41 |
0,17 |
|
873 |
9,98 |
8,63 |
7,20 |
5,78 |
4,42 |
3,18 |
2,11 |
1,22 |
0,52 |
|
923 |
25,30 |
21,90 |
18,31 |
14,74 |
11,33 |
8,21 |
5,49 |
3,19 |
1,37 |
|
973 |
58,21 |
50,47 |
42,36 |
34,20 |
26,42 |
19,23 |
12,91 |
7,59 |
3,27 |
|
1023 |
123,6 |
107,2 |
90,10 |
73,08 |
56,61 |
41,47 |
28,03 |
16,55 |
7,21 |
|
1073 |
244,3 |
212,3 |
179,1 |
145,2 |
113,0 |
83,18 |
56,49 |
33,57 |
14,72 |
Фазовая диаграмма « Р–х » может быть использована для анализа компонентов получаемых продуктов в зависимости от температуры и давления в процессе вакуумной перегонки, если режим дистилляции выбирается на основе VLE диаграмм, исходя из требуемого содержания металлов в дистилляте и остатке. Например, « Р-х »-кривые при 973 K, где давление изменяется в диапазоне 0,0027–64,57 Па, указывают на то, что возгоны и остаток достигают высокой степени разделения: при Р = 0,28–3,28 Па содержание Sb в остатке и, соответственно, Sn в конденсате составляет (7,242–93,05).10–7 мольной доли. По мере дальнейшего снижения давления количество примесей в возгонах и остатках, соответственно олова и сурьмы, возрастает. Эти результаты дополняют ранее полученные данные из « Т-х »-диаграмм Sn–Sb-сплава.
Термодинамические параметры Sn–Sb-сплава для диапазона исследованных температур определили по уравнению (7) (табл. 12, рис. 7). Молярная избыточная энергия Гиббса G, ^ для
Таблица 11. Рассчитанные значения Pgas , γSb , y Sn сплавa Sn-Sb для « P-х »-диаграмм
Table 11. Calculated values Pgas, γSb , y Sn alloy Sn-Sb for “P-x” diagrams
|
Т , К |
х Sn |
0,9 |
0,99 |
0,999 |
0,9999 |
|
γ Sb |
0,462 |
0,392 |
0,375 |
0,374 |
|
|
873 |
logР g , [Па] |
-0,286 |
-1,357 |
-2,377 |
-3.378 |
|
y Sn .10–7 |
0,685 |
8,960 |
94,68 |
950,1 |
|
|
γ Sb |
0,502 |
0,434 |
0,418 |
0,417 |
|
|
973 |
logР g , [Па] |
0,515 |
-0,548 |
-1,569 |
-2,565 |
|
y Sn .10–7 |
7,242 |
93,05 |
984,2 |
9764 |
|
|
γ Sb |
0,538 |
0,471 |
0,456 |
0,456 |
|
|
1073 |
logР g , [Па] |
1,168 |
0,11 |
-0,903 |
-1,886 |
|
y Sn .10–7 |
49,53 |
623,6 |
6489 |
62450 |
Таблица 12. Рассчитанные значения G ^ ,Н m .S m сплава Sn-Sb
. . .
Table 12. Calculated values G ^ ,Н ^ .S m alloy Sn-Sb
|
T , K |
- G m , Дж/моль |
||||||||
|
x Sn |
|||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
|
823 |
754,7 |
1353 |
1770 |
2017 |
2096 |
2007 |
1752 |
1333 |
748,3 |
|
873 |
752,6 |
1349 |
1766 |
2013 |
2092 |
2004 |
1749 |
1331 |
747,3 |
|
923 |
750,4 |
1346 |
1762 |
— 2008 |
2088 |
2000 |
— 1747 |
1329 |
— 746,5 |
|
073 7 IJ |
748,2 |
1342 |
1757 |
2004 |
2083 |
1997 |
1744 |
1327 |
745,6 |
|
1023 |
746,0 |
— 1339 |
1753 |
1999 |
— 2079 |
1993 |
1742 |
1325 |
744,7 |
|
1073 |
743,8 |
1335 |
1749 |
1995 |
2075 |
1990 |
1739 |
1323 |
743,7 |
|
-Н m, Дж/моль |
790,57 |
1411,2 |
1840,2 |
2090,5 |
2166,2 |
2064 |
1793,7 |
1365,9 |
763,15 |
|
S m , Дж/моль. К |
0,0435 |
0,0709 |
0,0851 |
— 0,0891 |
— 0,0851 |
— 0,0691 |
— 0,0509 |
— 0,0400 |
— 0,0181 |
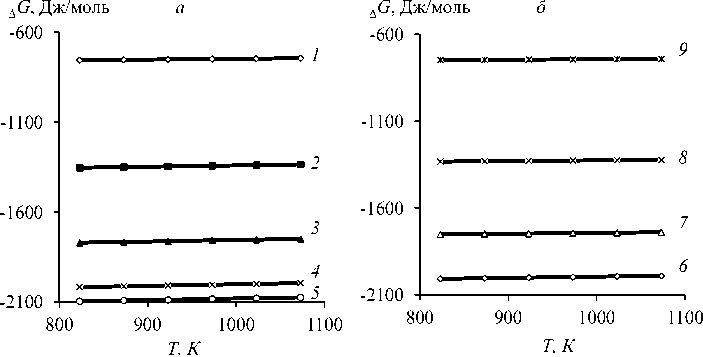
Рис. 7. Зависимость «д G - Т» для сплава Sn-Sb при x Sn: 0,1-0,9 (1-9 )
Fig. 7. Dependence “д G - Т ” for Sn-Sb alloy at x Sn: 0,1-0,9 ( 1-9 )
границы раздела «жидкость-газ» смеси i - j характеризует величину удерживания вещества в поверхностном слое при фазовом переходе, которая существенно зависит от состава Sn–Sb-сплава и температуры процесса. Энтальпия поверхностного слоя или избыточная внутренняя энергия ( HE m ) складывается из энергии Гиббса и теплоты образования поверхности ( ТSE m ), где S Em - энтропия, представляющая собой скрытую теплоту образования единицы площади поверхности (связанная энергия) в необратимом изотермическом процессе при температуре Т Отрицательные значения H Em свидетельствуют об экзотермическом характере процесса дистилляции компонентов Sn–Sb-сплава.
Относительно невысокие значения молярной избыточной энергии Гиббса - G ^ = 0,7442,096 кДж/моль в расплаве обусловлены низкими величинами межатомного взаимодействия компонентов i – j Sn–Sb-сплава в жидком состоянии, э-в: –( εij – εjj ) = –0,0081; –( εji – εii ) = 0,0070, что примерно на два порядка меньше энергии межатомного взаимодействия в твердой фазе [30].
Выводы
Фазовые диаграммы для Sn–Sb-сплавов различного состава при вакуумной перегонке рассчитаны на основе модели равновесия системы «жидкость-газ» ( VLE ), которая использует при расчете коэффициентов активности молекулярную модель объемного взаимодействия ( MIVM) . Существенное преимущество MIVM заключается в ее способности прогнозировать термодинамические свойства жидких сплавов, используя только коэффициенты активности для двоичных (бинарных) бесконечно разбавленных систем. Поэтому MIVM не использует эмпирические значения параметров, характеризующих потенциальную энергию парного взаимодействия. Для последующего практического использования важно оценить степень разделения и количественный состав продуктов с помощью фазовых диаграмм «температура – состав» ( Т-х ) и «давление- состав» ( Р-х), что позволит выбрать условия обработки исходных материалов для получения продуктов заданного состава.
Список литературы Равновесные системы "газ-жидкость" для сплава Sn-Sb при вакуумной дистилляции
- Berman A. Total Pressure Measurements in Vacuum Technology. New York: Academic Press, 1985. 380 р.
- Winkler O., Bakish R. Vacuum metallurgy. Amsterdam: Elsevier, 1971. 237 р.
- Jia G.-B., Yang B., D.-c. Liu. Deeply removing lead from Pb-Sn alloy with vacuum distillation. Transactions of Nonferrous Metals Society of China, 2013, 23(6), 1822-1831.
- Wang A., Li Y., Yang В., Xu В., Kong L., Liu D. Process optimization for Vacuum distillation of Sn-Sb alloy by response surface methodology. Vacuum, 2014, 109, 127-134.
- Dai Y.N. Vacuum metallurgy of nonferrous metals. Beijing: Metallurgical Industry Press, 2009. 72 p.
- Yang B., Kong L.-X., Xu B.-q., Liu D.-c., Dai Y.-N. Recycling of metals from waste Sn-based alloys by vacuum separation. Transactions of Nonferrous Metals Society of China, 2015, 25(4), 1315-1324.
- Liu D.C., B. Yang, F. Wang, Yu Q.C., Wang L., Dai Y.N. Research on the Removal of Impurities from Crude Nickel by Vacuum Distillation. Physics Procedia, 2012, 32, 363-371.
- Dai Y.N., Yang B. Non-ferrous Metals and Vacuum Metallurgy. Beijing: Metallurgical Industry Press, 2000. 40 p.
- Smith J.M., Van Ness H.C., Abbott M.M. Introduction to Chemical Engineering Thermodynamics, sixth ed. New York: McGraw-Hill, 2001. 749 p.
- Tao D.P. A new model of thermodynamics of liquid mixtures and its application to liquid alloys. Thermochim. Acta, 2000, 363, 105-113.
- Poizeau S., Kim H.J., Newhous J.M., Spatocco B.L., Sadoway D.R. Determination and modeling of the thermodynamic properties of liquid calcium-antimony alloys. Electrochim. Acta, 2012, 76, 8-15.
- Newhouse J.M., Poizeau S., Kim H., Spatocco B.L., Sadoway D.R. Thermodynamic properties of calcium-magnesium alloys determined by emf measurements. Electrochim. Acta, 2013, 91, 293-301.
- Miyazaki N., Adachi N., Todaka Y., Miyazaki H., Nishino Y. Thermoelectric property of bulk CaMgSi intermetallic compound. Journal of Alloys and Compounds, 2017, 691, 914-918.
- Materials Science and Technology. Eds. R.W. Cahn, P. Haasen, E. J. Kramer. Vol. 1. Structure of Solids. Ed. V. Gerold. VCH. Weinheim, 1993. 621 p.
- Hultgren R., Desai P.D., Hawkins D.T., Geiser M., Kelley K.K. Selected Values of the Thermodynamic Properties of Binary Alloys. ASM. Metals Park. OH. 1973. 847 р.
- Dai Y., Yang B. Vacuum Metallurgy for Non-Ferrous Metals and Materials. Metallurgical industry Press, Beijing, 2000 (in Chinese). 124 р.
- Yang H.W,. Yang B., Xu B.Q., Liu D.C., Tao D.P. Application of molecular interaction volume model in Vacuum distillation of Pb-based alloys. Vacuum, 2012, 86(9), 1296-1299.
- Jiang W.L., Zhang C., Xu N., Yang B., Xu B.Q., Liu D.C., Yang H.W. Experimental investigation and modelling of phase equilibria for the Ag-Cu-Pb system in vacuum distillation. Fluid Phase Equilibria, 2016, 417, 19-24.
- Nan C.B., Xiong H., Xu B.-q., Yang B.,. Liu D.C, Yang H.W. Measurement and modeling of phase equilibria for Sb-Sn and Bi-Sb-Sn alloys in vacuum distillation. Fluid Phase Equilibria, 2017, 442, 62-67.
- Zhao J.Y., Yang W., Nan C.B., Yang B., Liu, Xu B.-q. Kinetics of Pb evaporation from Pb-Sn liquid alloy in Vacuum distillation. Vacuum, 2017, 141, 10-14.
- Kong L.-X., Xu J., Xu B.-q., Xu S., Yang B. Vapor-liquid phase equilibria of binary tin-antimony system in vacuum distillation: Experimental investigation and calculation. Fluid Phase Equilibria, 2016, 415, 176-183.
- Nan C.В., Yang H.W., Yang B., Liu D., Xiong H. Experimental and modeling vapor-liquid equilibria: Separation of Bi from Sn by Vacuum distillation. Vacuum, 2017, 135, 109-114.
- Song B., Xu N., Jiang W., Yang B., Chen X. Study on azeotropic point of Pb-Sb alloys by ab-initio molecular dynamic simulation and Vacuum distillation. Vacuum, 2016, 125, 209-214.
- Zhang C., Jiang W.L., Yang B., Liu D.C., Xu B.Q., Yang H.W. Experimental investigation and calculation of vapor-liquid equilibria for Cu-Pb binary alloy in vacuum distillation. Fluid Phase Equilibria, 2015, 405, 68-72.
- Seith W., Johnen H. State diagram of the system Pb-Zn. Z. Elektrochem, 1952, 56, 140-143.
- Kong. L.-x.-q., Yang В., Xu В., Li Y.-f., L. Li. Application of molecular interaction volume model in separation of Pb-Sn-Sb ternary alloy by vacuum distillation. Transactions of Nonferrous Metals Society of China, 2013, 23(8), 2408-2415.
- Dong Z.W, Xiong H., Deng Y., Yang B. Separation and enrichment of PbS and Sb2S3 from jamesonite by Vacuum distillation. Vacuum, 2015, 121, 48-55.
- Kong L.X., Yang B., Xu B.Q., Li Y.F. Application of MIVM for Pb-Sn-Sb ternary system in Vacuum distillation. Vacuum, 2014, 101, 324-327.
- Kong L., Yang B., Xu B., Li, D. Liu Y., Dai Y. Application of MIVM for phase equilibrium of Sn-Pb-Sb system in vacuum distillation. Fluid Phase Equilibria, 2014, 364, 1-5.
- Баранов М.А. Сферическая симметрия электронных оболочек атомов и стабильность кристаллов. Электронный физико-технический журнал, 2006, 1, 34-48.


