Разделение ионов в комбинации стационарных полей — электрического квадрупольного и магнитного однородного

Первая публикация о возможности использования в масс-анализе квадрупольного поля появилась в 1953 г. [1], авторами которой были В. Пауль и его коллеги из Боннского университета, а позднее группа В. Пауля получает патенты на квадрупольный масс-спектрометр [2] и в течение ряда лет успешно развивает теорию этого нового устройства. Несмотря на столь давнюю историю квадрупольный масс-фильтр не утратил своих позиций и по сей день и занимает определенную нишу в парке масс-спектрометрических приборов. Технология изготовления, настройка прибора и его обслуживание настолько отработаны, что квадруполь используется широко и в сложных системах на предварительных этапах анализа, и как основной элемент масс-спектрометров. Подробно изучены различные режимы работы масс-фильтра, найдены эффективные решения разноплановых задач масс-анализа, определены оптимальные параметры этих режимов. И хотя массовое разрешение, достигаемое в квадрупольном масс-спектрометре, не столь велико, однако интерес к ним со стороны разработчиков не угасает.

Мы предлагаем ряд новых приложений и режимов работы квадрупольного масс-спектрометра, к которому прикладывается однородное магнитное поле. Далее будет показано, что в случае стационарных полей (электрического и магнитного) наблюдаются устойчивые траектории ионов. Кроме того, обнаружилось существование линейных многообразий в фазовом пространстве начальных данных, обеспечивающих финитность поперечных движений. В связи с этими обстоятельствами наметились идеи построения масс-спектро-

метрической стационарной системы на комбинации скрещенных полей, которую можно воспринимать как обобщение фильтра Вина с неоднородным электрическим полем и спиральными осевыми траекториями.

Данное теоретическое исследование построено в аналитической форме, и для удобства анализа движений уравнения приведены к безразмерным координатам и времени. Изложим подробнее используемую безразмерную модель движения.

БЕЗРАЗМЕРНАЯ МОДЕЛЬ ДВИЖЕНИЯ

Положим:

R = X i + Y j + Z k = £ • r = £ ( x i + y j + z k ) , t = T • t ,

где Х , Y , Z , t — размерные координаты и время; x, y, z, τ — безразмерные координаты и время; £ , T — выбранные линейный и временной масштабы. Поскольку в квадрупольном масс-спектрометре электрическое поле обычно предполагается периодическим, то в качестве единицы времени Т выгодно принять именно период колебания высокочастотного поля независимо от того, синусоидальное оно или какой-либо иной формы.

Потенциал квадрупольной системы можно записать тогда в виде

Ф =

Ф0 + Ф1 • f I

X ²

- Y

£

где Ф0 и Ф1 — размерные значения потенциала (в вольтах). В безразмерных параметрах последнее выражение можно переписать как ф —[ф0 +ф1 • f (т)]•(x2 -У2), f (т + 1)= f (т).

Вектор индукции можно представить как

B — B 0 • b — B 0 ( bii + b 2 j + b ₃ k ) ,               (4)

где В 0 — характерное, например максимальное, значение индукции внутри прибора на его периферии; вектор b — безразмерный и его компоненты — обязательно гармонические функции безразмерных координат x , y , z . Тогда в векторной форме уравнение движения:

m

T ² ’ r

^{— -} 2q [^ф 0 ^+ф 1 • f ( т ) ] ( ^{x -} y j ) + qB [ r X b ] ,

где точками обозначены производные по τ. Приводя коэффициенты к безразмерной форме, получим уравнение вида r = -[ц + V • f (т)](xi-yj) + Л-[Г Xb],(6)

где введены обозначения

2 q Ф T ²        2 q Ф Т ²

ц —          , V — о , Л — m I         m I

АНАЛИЗ ДВИЖЕНИЙ ИОНОВ В СТАТИЧЕСКИХ ПОЛЯХ

Исключим высокочастотную (ВЧ) компоненту поля ( Ф ₁ = 0) из уравнения (6), что равнозначно условию V — 0 . Имеем:

r — - ц( xi - y j) + Л • [r x b], ц — 2q^TL, Л — qBT.

m /2

Выбор Т можно подчинить каким-то более выгодным условиям, чем период ВЧ-поля:

т m 1 Г 2nm ) T

Л — 1 или T —---— — ----I — —.(8)

qB ₀  2 n ( qB ₀ J 2 n

Таким образом, мы принимаем в качестве физической единицы времени примерно 1/6 циклотронного периода Тц. В этих условиях ц — 2

m Ф ₀ q ^ B o² .

Система уравнений движения в стационарном случае при новом выборе Т примет простой вид x — -цх + yb3 -zb2, < y — цу + zb1 -xcb3,(10)

z — xc b ₂ - y b ₁.

Числа b1, b2, b3 следует связать условием b2 + b 22 + b 32 — 1.(11)

Интегрирование третьего уравнения системы (10) дает z — zo + b 2 •(x -x 0 )-b1 •( y - y 0 ).

Исключение z из первых двух уравнений системы (10) дает систему для поперечного движения вида x — - (ц + b 22) x + b1 b 2 y + b3 y - b 2 N, y — (ц - b2)y + b1 b2x - b3.x + b1 N,       (13)

N ^— z o + ^b 1 y 0 ^{- b} 2 ^x 0 .

В своем исследовании мы ограничимся рассмотрением только случая приложения к каналу квадруполя поперечного магнитного поля, оставив за рамками статьи другие варианты — продольное поле и более общий случай — косоугольное.

ПОПЕРЕЧНОЕ МАГНИТНОЕ ПОЛЕ

При условии b ₃ — 0 система (13) существенно упрощается:

x — -(ц + b 22) x + b1 b 2 y - b 2 N, y — (ц - b12) y + b1 b2x + b1 N,          (14)

N ^— z o + ^b 1 y 0 ^- b 2 ^x 0 .

В зависимости от соотношения параметров µ , b ₁ , b ₂ и комбинирования их знаков могут происходить различные динамические явления, весьма неочевидные. Разберем последовательно их в порядке нарастания сложности.

Ситуация 1 ( b ₁ — 0, b ₂ — 1 )

Пусть магнитное поле имеет ненулевую только у -компоненту b ₁ — 0, b ₂ — 1, b ₃ — 0. Присоединяя к системе (14) и уравнение по z (12), имеем

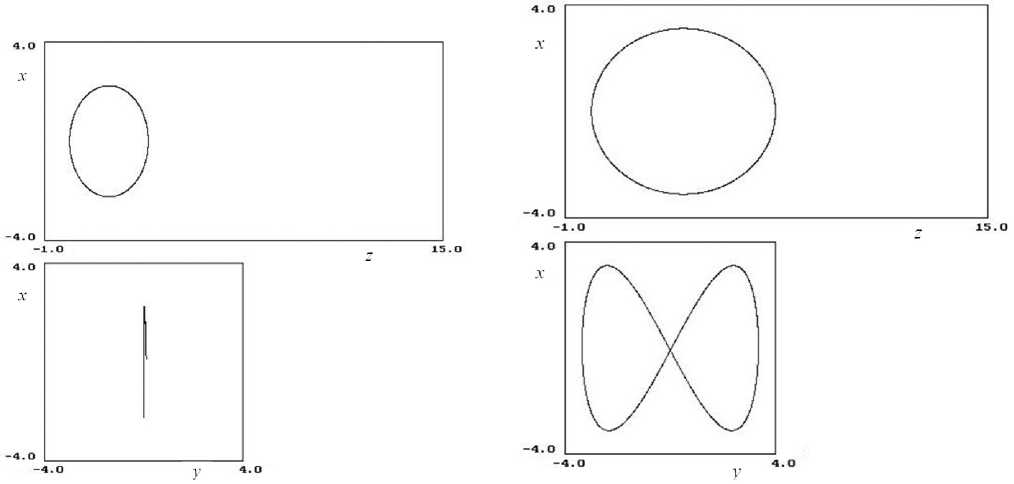
Рис. 1. Ловушечный режим движения.

Начальные условия: x 0 = 0.1, у 0 = 0.1, z ₀ = 0, w ₀ = ( x ₀ ² + y 2 + z 0 )/2 = 5. Параметры полей: ц = 0.5, Л = 1

Рис. 2. Движение ловушечного типа.

Начальные условия: x ₀ = 0.1, у ₀ = 0.1, z ₀ = 0, w ₀ = ( x 2 + у О + z 2 )/2 = 5, у₀ = 1.5. Параметры полей: ц = 0.2, Л = 1

x = —( ц +1) x — N, .у = цу, z = x + N;

N = z₀ ^— x₀.

Рассмотрим варианты решений этой системы (15) в зависимости от значения параметра µ .

Вариант а ( ц >  0 ) . В этом случае решение системы (15) будет иметь вид

z0 + цx         x

x = —----0 cos GT +—0 Sin GT - ц + 1         G

N

ц + 1

1 ( y='

A

+A

V ц J

• e

(

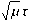
z = z0 + V

X

x0

ц+ 1J

+

µN ц+ 1

t +

z0 + цx          x0

+—0-----0 Sin GT--0- cos GT ,

G( ц + 1)         G2

где g = ц + 1.

В данных условиях вдоль оси X ионы колеблются с частотой σ со смещенным центром колебаний, по оси Y в общем случае наблюдается экспоненциальное разбегание, а по оси Z дрейф с колебаниями. Но если на начальные условия наложить требование N = 0 и "занулить" коэффициент во втором уравнении системы (17) при растущей экспоненте, то по осям X , Z будут наблюдаться чисто гармонические колебания с частотой g = ^ц + 1 , а вдоль оси Y ионы асимптотически приближаются к плоскости у = 0 (рис. 1).

Таким образом, при условиях

. ^у 0 =^- 'Гц У 0 , _ :^0 = ^x 0

и при любых x ₀, z ₀ в системе образуется ионная ловушка с финитным движением.

Вариант б ( ц <  0 ) . Знак ц можно поменять за счет изменения знака Ф ₀. Если

— 1 <  ц <  0,

то по обеим координатам x и y имеют место гармонические колебания с частотами с=71 -hi,   $=th.           (20)

По осям X, Z движение по-прежнему выражается формулами 1 и 3 в системе (17), но по Y будет выражение y = y 0cos VHT + yrs sin (21) µ

При условиях (20) ловушка образуется, если положить N = 0 и вместо условий (18) появится менее стеснительное ограничение

Z o = x 0 , (22)

а остальные начальные данные у 0 , у ₀, z 0 , x ₀ могут быть любыми. Рис. 2–5 иллюстрируют характер движений в образующейся ловушке.

Величина N = z 0 - x 0 управляет дрейфом вдоль оси Z , и скорость дрейфа тем меньше, чем ближе мы к условию (16). Траектория в этом случае представляет собой некий асимметричный клубок, медленно катящийся вдоль оси Z .

Этот режим можно очень интересно использовать в масс-спектрометрии, если учесть, что колебаниям с безразмерными частотами 71 + Н и 7Н отвечают реальные гармонические колебания ионов с частотами, однозначно связанными с массами m. Если канал квадруполя заполнен медленно катящимися клубками ионов, то на подходящем емкостном приемнике можно выделять электрические сигналы, спектральный состав которых несет

x

z

x

y

Рис. 3. Движение ловушечного типа.

Начальные условия: x ₀ = 0.1, у ₀ = 0.1, z ₀ = 0, w ₀ = ( Х 02 + у ₀ ² + Z ^ )/2 = 5, у ₀ = 1.5. Параметры полей: н = - 0.4, Л = 1

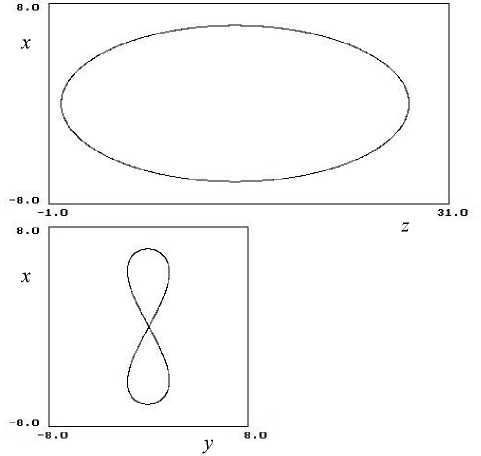
Рис. 5. Движение ловушечного типа.

Начальные условия: x ₀ = 0.1, у ₀ = 0.1, z ₀ = 0, w ₀ = ( x 0² + у ₀ ² + z ^ )/2 = 5, у ₀ = 1.5. Параметры полей: н = - 0.8, Л = 1

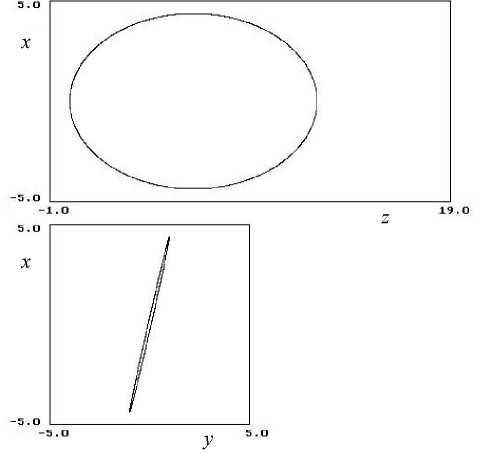
Рис. 4. Движение ловушечного типа.

Начальные условия: x ₀ = 0.1, у ₀ = 0.1, z ₀ = 0, w ₀ = ( Х 2 + у ₀ ² + z 2 )/2 = 5, у₀ = 0.7. Параметры полей: н = - 0.5, Л = 1

информацию о масс-спектре. Иначе говоря, в системе можно реализовать идею фурье-масс-анализ-атора (фарвитрона).

Вариант в ( 4 = - 1 ) . При условии 4 = - 1 сис-

1	µ	x    z 0 .      X 0        o-r .
X = —		и       и              0         , аа Т -L-
2	к	4 -1   ^Р ^e

тема (15) вырождается:

J X = — N , I У = ^- У ; z = x + N ,

и решение представляется в виде

N 2

X = ——Т + X 0Т + X0, y = y 0 cost + yosin т,

z = z₀ т + x ⁰ т ² - —т ³ + z ₀.

02       6       0

Здесь поведение ионов совсем другое. По осям X , Z имеет место ускорение, и только вдоль оси Y сохраняются гармонические колебания. Однако и тут все-таки удается организовать ловушку, наложив условия

+ —

|^{4 X} 0 z 0 1 ^{4 - 1}

У = У 0 c^os

у

z = —

2 σ

-

к

x ₀

-

1   4 ^X о

2 σ

^{+ z} 0

z ₀

-

к

-

x ₀

^

X0

4 4 - 1 у

y ₀

+

z ₀

µ

sin

x ₀

-

x ₀

• e

- ат

µ

τ ,

к

У

στ

• e

к

у

-

• e

- ат

µN

1 ^{4 - 1} 1 ^{Ц - 1}

τ .

Если "убить" коэффициент при e

N

1 ^{4 - 1}

+

στ

и

, (29)

N = 0 , то

получим ловушку при следующих условиях:

N = 0, z 0 = 0, x 0 = 0.          (25)

Отсюда очевидно: надо положить еще x 0 = 0.                   (26)

Произвольными остаются начальные данные y 0 , y 0 , z 0 . И в этом режиме можно образовать фарвитрон со своими возможностями.

Вариант г ( ц < - 1 ) . Система (15) дает заведомо экспоненциальные движения как по оси X , так и по оси Z , по Y сохраняются гармонические колебания. Выбором начальных данных можно "убить" растущую компоненту, и при этом появляется новый тип динамических колеблющихся траекторий. Рассмотрим все это подробнее.

Сначала перепишем систему (15):

X = (| 4 — 1 ) x - N ,

_ ^y = ^-| ⁴ У ;

z = X + N ,                    (27)

N = ^z0 - ^X 0 .

Положим, как и раньше, в тех же обозначениях a = 44-1, Ц > 1.         (28)

Интегрирование дает выражения:

• _ z 0 I 4 X 0

l x 0 У Й7^

_ z o - X 0 = 0,

или

Пример ловушечного режима приведен на рис. 6.

При z ₀ * X ₀ и выполнении первого условия из (33) имеет место дрейф вдоль оси Z , колебания по Y и асимптотическое стремление всех ионов к плоскости x = const. Рис. 7 иллюстрирует особенности такого дрейфующего движения.

Ситуация 2 ( b ₂ = 0, Ь 1 = 1 )

Теперь магнитное поле ориентировано вдоль оси Х , Ь 1 = 1, b ₂ = 0, b ₃ = 0. Система, составленная из (14) и (12), примет вид

X = - 4X ,

_ ^У = ( 4 ^- 1 ) у + N ; z = - y + N , N = z o + У 0 .

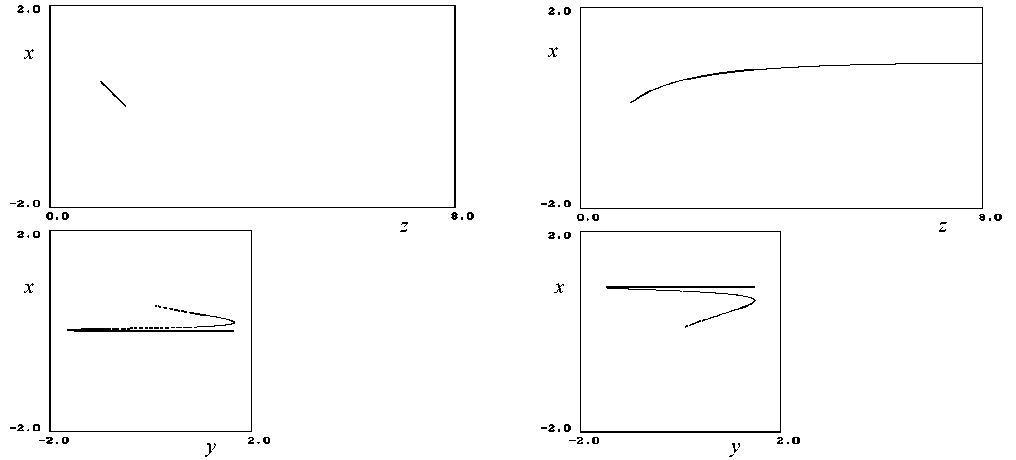
Рис. 6. Ловушечный режим.

Начальные условия: x0 = 0.5, y0 = 0.1, z 0 = 1.0, w0 = ( x2 + y2 + z02) /2 = 3. Пара метры полей: ц = -2, X = 1

Рис. 7. Режим удержания в плоскости XY и дрейф вдоль оси Z .

Начальные условия: x 0 = 0.1, y ₀ = 0.1, z ₀ = 1.0, w ₀ = ( x 2 + y ₀ ² + z ₀²)/2 = 3, z₀ = 1. Параметры полей: ц = - 2, X = 1

Чередованием знаков µ и переименованием переменных эту ситуацию легко привести к предыдущей, и потому ее разбирать ни к чему.

Ситуация 3 ( b₁ * 0, b ₂ * 0, b₃ = 0 )

Пусть магнитное поле произвольно направлено по отношению к осям Хи Y , b 1 * 0, b ₂ * 0, b ₃ = 0.

Система (14) и уравнение (12) примут вид

Ее решения суть

A = , b 2 N    , B = , b - N    .

b ² - b ₂ ² - ц          b 1 ² - b ₂ ² - ц

Положим ц * b2 - b22

и займемся однородной системой:

x = - ( ц + b ₂²) x + b 1 b ₂ y - b ₂ N , y = b j b ₂ x + ( ц - b 2 ) y + b j N ;

x = - ( ц + b ₂²) x + b 1 b ₂ y , y = b 1 b ₂ x + ( ц - b 2 ) y .

z = b ₂ x - yb 1 + N ,

N = ^z0 ^{- b} 2 x 0 ^{+ b} 1 y 0 .

Система (36), состоящая из двух первых уравнений, неоднородна, и ее решение состоит из частного решения x 1 = A = const, y 1 = B = const и общего решения однородной части. Для определения А и В имеем алгебраическую систему

В соответствии с методом Эйлера ищем частные решения вида

' x = P • e^{k T} , . y = Q • e k ,

где P , Q , k — неизвестные пока числа. Подстановка (41) в (40) дает следующую однородную линейную алгебраическую систему относительно P , Q :

- ( ц + b ₂ ² ) A + b 1 b ₂ B = b ₂ N , b 1 b ₂ A + ( ц - b 12 ) B = - b 1 N .

'( k ² + ц + b 2 ) • P - b 1 b 2 Q = 0,

^{- b} 1 b ₂ P + ( ^{k 2 - ц} + ^b 1 ² ) • Q = 0.

Определитель этой системы обязан обращаться в нуль, что дает характеристическое уравнение относительно показателя k :

в — b 2 x 0 + b 1 y 0 , Y ^{— b} 2 x 0 ^{+ b} 1 y 0 .

k ² + ц + b 22 - b 1 b ₂

- b 1 b ₂         k ² - ц + b 1

Развернув (43) и приняв во внимание соотношение lb + b 22 — 1, получим характеристическое уравнение

С помощью связи (50) можно исключить из первого уравнения системы (47) функцию y , а из второго уравнения системы (47) функцию х : возникает система из двух изолированных уравнений второго порядка относительно x и y по отдельности. С учетом соотношения b 1 ² + b ₂ ² — 1 выводим:

k ⁴ + k ² - ц ² + ц ( b 12 - b 22 ) = 0.         (44)

Его корни:

x — - x + b ₂ ( ат ² + вт + Y - N ) , y — - y + b 1 ( ат ² + вт + Y + N ) •

^k 1 =

—

—+

4 ^{- ц} ( b ^- b 22 ) + ^{ц 2},

^k 2 = ^{- k} 1 ,

k 3 —

^- 4 ^{- ц} ( ^b1 ^{- b} 22 ) + ^{ц 2},

Общее решение однородной части здесь, очевидно, одного типа — гармонические колебания с частотой о — 1. Неоднородная система имеет частное решение x ^* , y ^* в виде квадратичных полиномов, которые легко найти методом неопределенных коэффициентов.

Положим:

k 4 — - k 3 .

Все радикалы понимаются как арифметические положительные величины.

x * ^— g 1 ^{т 2 +} g 2 ^{т +} g 3 , y * — s ₁ т ² + s ₂ т + s ₃.

Подстановка (52) в (51) дает систему

Случай

Ц — b 1 ² - b 22 ,                   (46)

когда k 1 — k 2 — 0, является вырожденным, и он отвечает случаю обращения в нуль определителя алгебраической системы (37). Запишем два первых уравнения системы (36), выразив µ из условия (46), получим в этом случае x — - b12 x + b1 b2 y - b2 N, y — b1 b2 x - b2 y + b1 N.

Умножим первое уравнение из (47) на b2, а второе — на b1, и сложим результаты. Получим интегрируемое соотношение b2x + b 1 y — (b 12 -b22 )• N.           (48)

Интегрируя (48) с учетом начальных данных x0, x0, y0, y0 в момент т — 0, находим соотношение b 2 x + b1 y — ат2 + вт + Y,         (49)

² g i ^{— -} дт ^{2 -} g 2 ^{т -} g 3 ^{+ b}2 ^{ат 2 + b} 2 ^{вт + b} 2 ( Y ^- N ) , 2 s 1 —- s₁т ² - s ₂ т - s 3 + ^ ат ² + b₁вт + b 1 ( y + N ) .

Приводя к нулю коэффициенты при линейно независимых степенях τ , получим уравнения для всех g и s :

g 1 — аb 2 , g 2 — вb 2 , g 3 — b 2 ( Y - N ) - 2 аb 2 , s 1 — аb ₁, s ₂ — вb ₁, s ₃ — b 1 ( y + N ) - 2 аb 1 .

**

Следовательно, частное решение x , y :

x * — b ₂ ( ат ² + вт + Y - N - 2 а ) , y * — b 1 ( ат ² + вт + Y + N - 2 а ) .

Общее решение для (51) можно теперь записать с учетом (55) в виде x—Ц cos т+M2sinт+b2 (ат2 + вт+Y - N - 2а), y—L cos т+L2sinт+b1 (ат2 + вт+Y+N - 2а).

b ²

где а — N ¹

-

b ²

2 и

Выразим М 1 , М 2 , L 1 , L 2 через начальные данные, получим окончательно x ( т ) , y ( т ) в виде

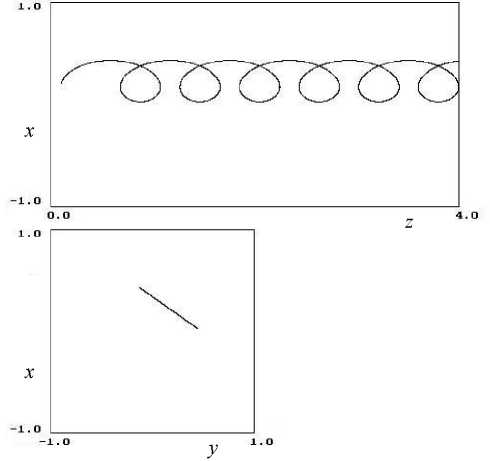
Рис. 8. Финитное движение в плоскости XY и дрейф вдоль оси квадруполя.

Начальные условия: x 0 = 0.2, y 0 = 0.2, z 0 = 0.1, w ₀ = ( x ₀ ² + y ₀ ² + Z 2 )/2 = 3, x ₀ = 0.2. Параметры по

^b 2 ^x 0 ^{- b} 1 У 0 = z 0 , .^b 2 ^x 0 ^{+ b} 1 ^y 0 = ^0.

Рис. 8 демонстрирует режим удержания ионов в канале квадруполя в поперечной плоскости, при этом ионы двигаются к выходу канала.

Наши дальнейшие исследования показали, что при поперечном магнитном поле, направленном произвольно относительно осей X и Y , движение в плоскости XY ( x ( т ) , y ( т ) ) является устойчивым, если выполняется условие

0 <  ц <  b 1 ² - b ₂². (60)

Вне этого интервала все траектории неустойчивы. Используя неравенство (60), можно высчитать интересный принцип фильтрации ионов, исходя из переменного интервала масс. Учтем, что параметр μ есть

ц = 2

m Ф ₀ q ^ 2 B 0 ².

Тогда для реальной массы m с помощью (60) и (61) мы получим неравенство

лей: ц = - 1, X = 1, b = ^3, b 2 = J23, b 3 = 0

0 < m <

' b 1 ² - b 2 ) q t 2 Bj_L

I 2 J  Ф 0

x = (x0 - b2 ( y - N - 2a)) cos т +

+ (x0 - вЬ2) sinт + b2 (ат2 + вт + Y - N - 2a), y = (y0 - b1 (Y + N - 2a)) cos т +

+ ( У 0 - eb ] ) sin т + b j ( ат ² + вт + Y + N - 2 a ) .

Движение по осям X , Y будет финитным, если коэффициенты α и β сделать нулевыми, что дает при помощи (50) следующие условия на параметры системы:

a = N (b ² - b Л = 0,

^{( 1      2} )      ,                  (58)

^в = ^b 2 x 0 ^{+ b} , ^y 0 = 0.

Случай ( b j ² = b 2 ) мы отбросим, т. к. в этом построении ц = b ² - b ₂ ² и нулевая "масса" ц не фи-зична.

Если взять N = 0 и раскрыть N по третьей формуле системы (14), то получим из (58) условия на начальные данные, удерживающие "массу" ц = 1 в канале квадруполя:

Меняя Ф ₀ при замороженных b 1 , b ₂ и B ₀, мы варьируем верхнюю границу диапазона масс ионов, отфильтрованных в квадруполе, и на детекторе фиксируется некий интегральный спектр, из которого реальный спектр масс получается процедурой электрического дифференцирования.

ЗАКЛЮЧЕНИЕ

Итак, мы изучили движения ионов в статическом квадруполе и приложенном к нему поперечном магнитном поле. Оказалось, что при определенных параметрах полей и комбинации начальных условий движения ионного пакета можно добиться удержания в поперечной плоскости ионов одного сорта. Наш общий физический вывод можно свести к нескольким положениям.

• •    Эта система допускает режимы ловушки ионов с финитными движениями.

• •    В системе может реализоваться режим интегральной фильтрации с управляемой границей спектра сепарируемых масс с электрической разверткой изменением Ф ₀, при неизменном магнитном поле B 0 .

• •    В системе могут реализовываться фарви-тронные режимы.