Разгон гиророторов и включение избыточного кластера гиродинов в контур управления ориентацией информационного спутника

После отделения информационного спутника от ракеты-носителя и механического раскрытия его солнечных батарей (СБ) космический аппарат (КА) начинает вращаться с вектором угловой скорости to произвольного направления в связанной с корпусом КА системе координат (ССК). Для ориентации КА в орбитальной системе координат (ОСК) выполняются начальные режимы, где обычно выделяют этапы успокоения (остановки вращения), определения углового положения КА по внешним ориентирам, поворотных маневров для приведения ориентации КА к заданной в ОСК и поддержания такой ориентации при подготовке бортового оборудования системы управления ориентацией (СУО) для последующего выполнения основных режимов. Например, начальные режимы ориентации геостационарного спутника связи SESAT [1] выполнялись с помощью датчиков угловой скорости, приборов ориентации на Солнце и Землю, двигательной установки (ДУ) на основе реактивных двигателей (РД) малой тяги с широтноимпульсным управлением для совмещения ССК с ОСК посредством двух одноосных поворотных маневров [2] и последующей угловой стабилизации КА в ОСК при разгоне ротора силового гироскопического стабилизатора в виде реактивного двигателя-маховика (ДМ) в двухстепенном кардановом подвесе [3].

В СУО маневрирующих информационных КА (в частности, спутников землеобзора) применяются электромеханические исполнительные органы в виде избыточных кластеров крат-

Сомов Сергей Евгеньевич, научный сотрудник отдела «Динамики и управления движением».

ных схем 3-SPE (группа 3 ножничных пар – 3 Scissored Pair Ensemble ) или 2-SPE на основе соответственно трех либо двух пар двухстепенных силовых гироскопов – гиродинов (ГД) с коллинеарными осями подвеса [4,5]. Энергетические возможности системы электропитания КА в начале его миссии не позволяют выполнить одновременный разгон роторов всех ГД составе силовых гироскопических кластеров (СГК) указанных схем, доступен разгон гиророторов до номинального значения h _g их собственного кинетического момента (КМ) лишь для пар ГД.

В работах [6 - 9] представлен метод разгона роторов ГД в составе таких СГК, когда оси гиророторов и угловые положения ГД относительно осей их подвеса зафиксированы в корпусе КА с помощью арретиров сразу в «парковом» состоянии (парке) СГК, которому соответствует значение вектора его КМ H = L h _p = 0 при h p = 1 h p 1 = h _g , где индексом p отмечен номер ГД. Здесь применяется пошаговый разгон гиророторов в циклах последовательности пар ГД, при завершении каждого такого цикла выполняется условие H = 0 . При этом проявляются инерционные возмущающие моменты из-за разгона гиророторов пар ГД и гироскопические связи каналов углового движения спутника, стабилизируемого в ОСК с помощью ДУ, естественно с расходом топлива РД.

В работе [10] предложена и исследована схема выполнения начальных режимов ориентации информационного спутника с применением бесплатформенной инерциальной навигационной системы (БИНС), корректируемой сигналами кластера звездных датчиков и навигационных систем ГЛОНАСС/GPS, двигательной установки на основе 8 РД с широтно-импульсным управлением, кластера четырех ДМ и магнитного привода с цифровым управлением. Здесь успокоение КА выполняется в инерциальной системе координат (ИСК) с помощью ДУ, далее проводятся инициализация БИНС с автономным определением как ориентации, так и расположения КА в ИСК, инициализация и включение кластера ДМ в контур управления ориентацией КА; этот режим завершается угловой стабилизацией КА в ИСК и расчетом на борту КА параметров потребного пространственного поворотного маневра КА на заданном интервале времени с краевыми условиями общего вида, который реализуется СУО с последующей угловой стабилизации спутника в ОСК.

В данной статье впервые предлагается метод разгона роторов ГД и приведения СГК кратных схем в парковое состояние без создания инерционных и гироскопических возмущающих моментов при угловой стабилизации корпуса спутника в ИСК с помощью двигательной установки. Приводятся результаты исследования процессов при разгоне роторов ГД, приведения в парк и включения СГК по схеме 3-SPE в контур управления ориентацией спутника на солнечно-синхронной орбите.

МОДЕЛИ И ПОСТАНОВКА ЗАДАЧИ

Стандартным образом вводятся ИСК, ОСК и ССК O xyz , корпус КА с фиксированным положением панелей СБ считается твердым телом с тензором инерции J . Вводятся также ортогональная каноническая система координат СГК O x g y g z g , для простоты совпадающая с ССК O xyz , и отсчет углов ГД в _p относительно осей их подвеса, рис. 1. Используются обозначения col() = { • } , line() = [ • ] , ( • ) * , [ a x ] и о ,~ для векторов, матриц и кватернионов, индексы i = 1,2,3 = 1 ^ 3 для осей ССК, применяется вектор модифицированных параметров Родрига (МПР) о = { о i } = е tg( Ф /4)

собственного поворота, который однозначно связан с кватернионом Л ориентации КА в ИСК прямыми О = X / (1 + X ₀) и обратными X _о = (1 -о ²)/(1 + о ²) , X = 2 о /(1 + о ²) соотношениями.

Модель углового движения КА принимается в виде

■

Л = Л о ®/2 ;

Jto = -[to x]G + Mg + Me + Md.

Здесь G = J to + H является вектором КМ электромеханической СУО, где столбец H = { Н i } представляют КМ СГК; M ^e - вектор момента двигательной установки на основе восьми РД [9], которая обладает возможностью одновременно создавать векторы внешних сил и моментов произвольного направления в ССК за счет широтно-импульсной модуляции (ШИМ) тяги РД; вектор M ^g = { M g } управляющего момента СГК формируется в виде M ^g = — H , где ( • ) - символ локальной производной по времени, а вектор M ^d представляет внешние возмущающие моменты.

Каждый РД с номинальным значением тяги Pm, одинаковым для всех РД, имеет ШИМ тяги pp (t) = PmPWM( t -Te tr ,Tm ,v pr) Vt e [tr, tr+1), p = 1 ^ 8, с периодом ТЦ и временным запаздыванием Tzu. Здесь vpr является дискретным входным сигналом и функции sign v„, t e [t,t + t_ _)

PWM( t,t_r, T _m ,v _p r )          ^pr r r ^pr/ ;

^      ⁰        t ^{e [} t r ⁺ T p r , t r + 1 ⁾

о

I v |< г pr

m ,

m

т(т)= pr m

sat(?;e,|vpr |) |vpr| > t где tr = rT, tr+i = tr + ТЦ ; r e No = [0,1,2,3...) . Вектор момента ДУ формируется по соотношению Me =E [pp x] p p (t), p = 1 ^ 8, где

— с обозначениями орта Эйлера e и угла ф и p p pp (t) = -pp (t)ep с ортом оси сопла ep

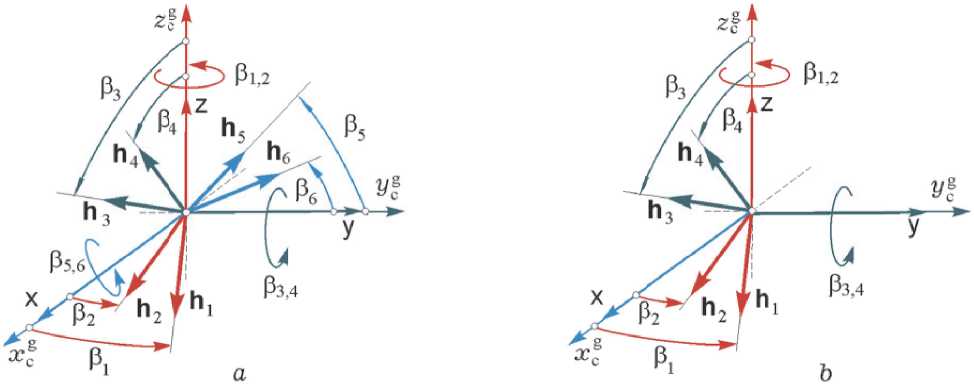
Рис. 1. Каноническая система координат СГК и отсчет углов ГД в схемах 3-SPE ( a ) и 2-SPE ( b )

вектор тяги p -го РД и радиус-вектор точки ее приложения в ССК, соответственно.

Для схемы 3-SPE (см. рис. 1 a ) введем обозначения проекций ортов КМ каждого ГД на оси системы координат O x ^g y ^g z ^g СГК

x1 = Cj = cos P1; x2 = C2 = cos P2; y1 = S1 = sin P1;

y2 = S2 = sin P2; x3 = S3 = sinP3; x4 = S4 = sin P4;

z ₃ = C ₃ = cos P ₃ ; z ₄ = C ₄ = cos P ₄ ; y ₅ = C ₅ = cos P ₅ ;

У6 = C6 = го<; z5 = S5 = sinP5; z6 = S6 = sinP.

Тогда вектор нормированного КМ такого СГК

h(P) = H(P) /hg, где столбец в = {pp }, p = 1 ^ 6, и градиентная матрица Ah (в) = dh / dp пред- ставляются в виде

x ■ C1 + C2 + S3 + S4 h = y = S 1 + S 2 + C5 + C6 .z. . C3 + C4 + S5 + S 6 _ законах их настройки; (ii) разработке алгоритмов наведения и управления ориентацией КА с помощью ДУ при переводе его углового положения из произвольного, достигнутого при завершении режима успокоения, в такое угловое положение в ИСК, при котором нормаль к плоскости панелей СБ направлена на Солнце; (iii) разработке метода разгона роторов ГД и приведения СГК кратных схем в парковое состояние без создания инерционных и гироскопических возмущающих моментов при угловой стабилизации корпуса спутника в ИСК с помощью ДУ; (iv) анализе динамических процессов при включении СГК в контур цифрового управления ориентацией спутника.

ПАРКОВЫЕ СОСТОЯНИЯ СГК

Вводятся обозначения xJ2 = x, + x2; x34 = x3+x4;

У 12 = У 1 + У 2 ;

	■- S 1	- S - 2	C 3	C 4	0	0 "
A h ( p ) =	C 1	C- 2	0	0	- S 5	- S 6	•
	0	0	- S 3	- S 4	C 5	S 6 .
Для схемы		2-SPE	(см.	рис.	1 b )	столбец

~ ^x 12

^y 56    ^y 5 + ^y 6 ; ^z 34    ^z 3 + ^z 4 ;

x 12

~

; x 34

x 34

—

z 34

^z 56 = ^z 5 + ^z 6 ;

~

; ^y 12 =

У 12

У 56 =

У 56

—

P = { p p } , p = 1 ^ 4 и

.

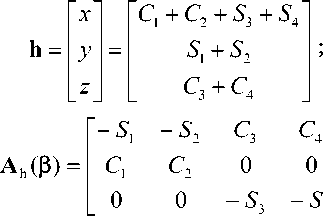
Z 56

~

; ^z 34

z 34

; ^z 56

z 56

4 _

и компоненты явного векторного стройки f p ^{( p )} = ^{ f_p 1 , f _{p 2} , f p J = 0 3-SPE принимаются в виде [5]

~ _~    ~ ~ fp1(P) — x12 x34 + P(x12 x34

закона на-

СГК схемы

—

1);

f p 2(P) = У 56 — У12 +P( У56 У12

^{— 1) ;}

При цифровом управлении СГК u k ( t ) = {u pk ( t )} с периодом Tu , где ^u pk ⁽ t ⁾ = ^u pk V t e [ tk , tk + 1 ) , t_k + i = tk + T_u и k e N₀ , когда управлением считается вектор p = u g скоростей ГД относительно осей их подвеса, кусочно-непрерывный управляющий момент СГК формируется по соотношениям

M k ( t ) = - h _g A h ( p ( t ) u k ( t ) ; p ( t) = u k ( t ) • (2)

Сингулярные состояния этой схемы возникают при таких угловых положениях ГД, когда матрица Грамма ^{G ( p )} = A h^{( p ) A} h^{( p )} теряет полный ранг, т.е. при G = det( G ( p ) = 0 . Важной проблемой управления СГК избыточной структуры является выбор функции распределения вектора КМ СГК между ГД – закона настройки СГК. Наиболее рациональными [4,5] являются явные законы настройки, когда все характеристики движения ГД получаются по аналитическим соотношениям.

Задача статьи состоит в (i) определении парковых состояний СГК обеих схем при явных fp 3(P) = ~34 — ~56 +P(~34~56 — 1), где постоянный параметр p удовлетворяет условию 0 < p < 1. Данный закон настройки обеспечивает отсутствие сингулярных состояний СГК для всех внутренних точек области вариации вектора его суммарного КМ. Для представления условий однозначной разрешимости уравнения h(P) = h, где h = {x, y) z} является известным вектором-столбцом, относительно синусов и косинусов углов p всех шести гиро-динов, вводятся обозначения

Р 12 = V^{4 — (} x 12 ⁾ ’ q 12 = V^{4 — ( У} 12 ⁾ ’

Р 34 = V^{4 — ( z} 34 ⁾ ; q 34 = V^{4 — (} x 34 ⁾ ;

р 56 = V^4— 1 у 5« >²; q 56 = V^4— < z 56 >²;

, .x l^ x-, .x Z^ x-, ₌у 1^ у. ^x 12       2    ’ x 34       2    ’ x ⁵⁶       2    ’

У — A У . - Z + A z . - z — A z , y12       2    ’ z34      2    ’ z56       2    ’ dx = Чп+p34’ dy = q56+Р12’ dz = q34+p56.

Условия разрешимости векторного уравне- ния h(P(t) = h(t)

имеют вид

A , - d x {1 - [1 - 4 p (( q ^ - p _M)( x /2)

+ p ( q^p 34 - ( x /2) ² ))/ d ²]^1/2 }/ p ’

A y - dy {1 - [1 - 4 p (( q ₅₆ - p i2 )( y /2)

+ p ( q 56 P 12 - ( y /2)²))/ d ²]^1/2}/ p ’

A z - d z {1 - [1 - 4 p (( q 34 - p 5б )( z /2)

+ p(q34P56 -(z/2)2))/dzT2}/p и при введении столбца А = {Ax, А , Az} очевидным образом преобразуются к нелинейному векторному уравнению А = Ф(h, А). Получить аналитическое решение этого уравнения для определения углов Pp ГД при парковом состоянии СГК весьма затруднительно, но его численное решение достигается практически мгновенно по методу простой итерации – при рациональном выборе начального точки достаточно лишь 2-3 итераций для получения результата с приемлемой точностью.

Далее при введении обозначений

X + A x .    3     У ^{- A} y .    _ I 2 , ,2 .

^a 1      2    ’ b 1       2 ’ c 1 ^a 1 ⁺ b 1 ’

П. Г, _      z + A_ , x -AT _ d 1 V4 c1 / c1 ’ a 2      2 ’ b2      2 ’

/-;   2             2         y + A y c 2 — Va 2 + b 2 ’ d 2 — V 4 - c 2 / c 2 ’ a 3 —   2   ’ b3 = z 2 z ; c 3 - Vа 2 + b3 ^ d 3 - V 4 - c2 / c 3

вычисление синусов и косинусов углов в _р всех шести ГД выполняется по явным аналитическим соотношениям

1-я пара (ГД1 и ГД2):

_ ai - dibi     _ bi + di ai , xi        ~     ;y 1        ~     ;

x 2	a 1 + d 1 b 1	b r	- d 1 a 1
	=     2     ; y 2 =		2      ;
2-я пара (ГД3 и ГД4):
x 3	_ b 2 + d 2 a 2 _ „ _	a 2	- d 2 b 2
	=      2      ; z 3 =		2
x 4	_ b 2 - d 2 a 2 _ _ _	a 2	+ d 2 b 2
	=     2      ; z 4 =		2
3-я	пара (ГД5 и ГД6):
	a 3 - d 3 b 3	b 3	+ d 3 a 3
y 5	=     „      ; z3 = 2         5		2
	_ a 3 + d 3 b 3 _ _ _	b 3	- d 3 a 3
y 6	=     2     ; z 6 =		. 2

Положение нечетных ( p = 1,3,5) и четных ( p = 2,4,6) ГД в трех парах i = 1 ^ 3 удобно представить углами a i = ( Р ₂ i - 1 + P 2J /2 и 5 i = ( Р ₂ i - 1 - Р ₂ i ) / 2 , i = 1 ^ 3 , которые поясняют применяемое выше наименование «ножничной пары» - угол a i определяет центральную линию ai «ножниц», а углы ± 5 i - положения векторов КМ h ₂ i - 1 и h ₂ i относительно линии ai в i -ой паре ГД.

Парковое состояние СГК по схеме 3-SPE приведено на рис. 2 a . Здесь векторы КМ всех 3 пар ГД h i = h ₂ i - 1 + h ₂ i с одинаковыми модулями и концами в точках A , B и C принадлежат плоскости P , которая содержит начало системы координат СГК, причем векторы h _i направлены по линиям a_i .

Для СГК по схеме 2-SPE при скалярном законе настройки f _{p 1} ( Р ) = х₁₂ - х₃₄ + p (x₁₂x₃₄ - 1) - О аналитическое решение, представленное первым соотношением в (3), зависит параметра р . Парковое состояние этой схемы приведено на рис. 2 b , где не показаны центральные линии a 1 и a ₂ двух ножничных пар, которые определяются углами a 1 = 0 и a ₂ = п , а также углы 5 1 = 5 2 в парах ГД.

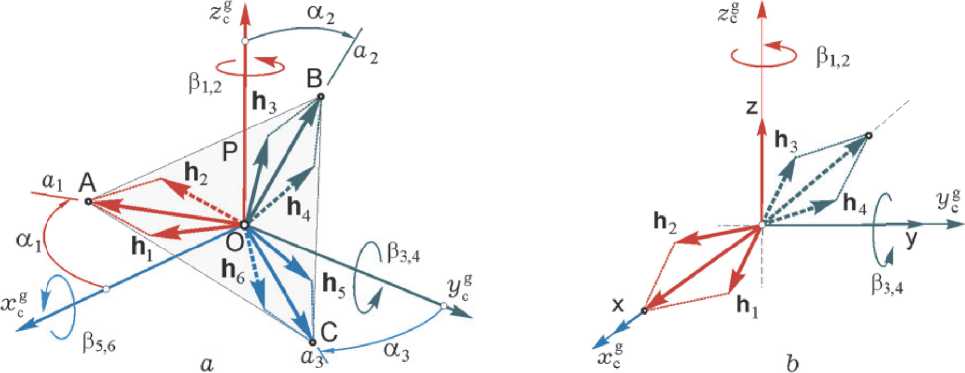
Рис. 2. Парковые состояния СГК кратных схем 3-SPE ( a ) и 2-SPE ( b )

НАВЕДЕНИЯ И УПРАВЛЕНИЕ КА ПРИ ОРИЕНТАЦИИ СБ НА СОЛНЦЕ

После окончания режима успокоения КА (остановки его вращения с точностью ≈ 0,05 град/с), включения БИНС с определением ориентации КА, его расположения в ИСК, а также положения Солнца, замыкания контура стабилизации углового положения КА с широтноимпульсным управлением ДУ и завершения переходных процессов далее на некотором интервале времени t е [ t i ^p , t f ] должен выполняться разворот спутника в такое положение, при котором нормаль к плоскости панелей СБ направлена на Солнце. Соответствующий закон пространственного углового наведения КА в ИСК синтезируется на основе простой кинематической модели

Лp = Лp оюp/2 ; op = ep

с заданными краевыми условиями

Л ^p ( t i ^p ) = K ^p ; to ^p ( t i ^p ) = 0 ;

Л ^p ( t _f ^p ) = Л ^p ; to ^p ( t^p ) = 0

и ограничениями на модули вектора угловой скорости to ^p ( t ) и кусочно-постоянного вектора углового ускорения е ^p ( t ) . В результате получается угловое наведение КА по кратчайшему пути – при кватернионе разворота Л ’ ( 1 0 , 1 * ) = Л ^Р о Л p программное угловое движение КА представляется его вращением вокруг орта е * = 1 * / sin( ф * /2) оси Эйлера на угол ф * = 2 arccos( X * ) .

Если задано программное угловое движение КА Л ^p ( t ), го ^p ( t ), e ^p ( t ) = Ю ^p ( t ) - закон его углового наведения в ИСК, то кватерниону рассогласования E = ( e ₀ , e ) = Л ^p о Л с вектором e = { ei } соответствует вектор параметров Эйлера E = { e о , е } , матрица C ^e( E = 1 ₃ - 2[ e x ] Q 0 , где Q _e = I ₃ e ₀ + [ e x ] , и вектор погрешности ориентации 5 ф = {5ф i } = { 2 e ₀ ei } .

После дискретной фильтрации измеренных БИНС с периодом T_q значений вектора углового рассогласования е _l = - 2 e _{0 l} е _l , l е N₀ , формируются значения вектора е ^f , r е N₀ , дискретного закона широтно-импульсного управления ДУ с периодом T U :

g r + 1 = Bg r + C s 0 ; m r = Kg r + P e ⁰; (5) M ' = o _r x J o _r + J ( C r e p + [ C> p х ] ю _r + m _r ).

Здесь матрица Ce = Ce(Er) и используются диагональные матрицы K , B , C и P . Далее импульс вектора потребного момента ДУ «пересчитывается» в столбец длительностей Tr = {тpr} включения РД Vt е [tr, tr+1), кото- рые используются при ШИМ тяги всех восьми РД с формированием вектора управляющего момента Mr( t) = E [pp x] pp (t) двигательной установки.

РАЗГОН РОТОРОВ И ПРИВЕДЕНИЕ СГК В ПАРКОВОЕ СОСТОЯНИЕ

Для СГК по схеме 3-SPE в плоскости изменения КМ каждой i -ой паре ГД введем линии b_i , ортогональные линиям a_i , см. рис. 3 a , и будем считать, что направления осей роторов нечетных ( p = 1,3,5) и четных ( p = 2,4,6) ГД в парах i = 1 ^ 3 зафиксированы в корпусе КА с помощью арретиров по линиям b_i при углах ГД относительно осей их подвеса в ₂ i - 1 = в ₂ i — п , так как согласно применяемой стратегии отсчета углов гиродинов нечетные ГД в парах всегда перемещаются впереди четных, см. рис. 1 и рис. 3 a .

При последовательном разгоне роторов в парах ГД с одинаковыми ускорениями вплоть до номинального значения h _g их собственных КМ инерционные возмущающие моменты таких гиророторов компенсируются. Поэтому в результате КМ роторов всех шести ГД принимают значения h _g без влияния их инерционных возмущающих моментов на угловое движение корпуса КА и при отключении арретиров гиродинов СГК становится готовым для приведения в парк.

При развороте двух ГД c противоположными векторами КМ в i -ой паре в разные стороны с одинаковыми скоростями относительно осей подвеса создаваемые ими гироскопические моменты складываются и вектор КМ h i ( t ) этой пары ГД изменяется вдоль центральной линии a_i , см. рис. 3 b . Поэтому в процессе приведения СГК в парк с условиями Н ( t ) = 0 и M ^g( t ) = - Н ( t ) = 0 рационально выполнять указанные развороты векторов КМ гиродинов во всех трех парах одновременно в следующей последовательности: 1) все шесть ГД разворачиваются в соответствующих направлениях с одинаковыми постоянными угловыми скоростями до значений ^их углов в 2 _/ ._ ₁ = e 2 i — i - X , e 2 i = e 2 i + X в парах i = 1 ^ 3 с заданным постоянным углом χ , далее принимается χ = 1 град; 2) задается потребный управляющий гироскопический момент СГК M ^g ^ 0 и включается закон его настройки, который автоматически приводит СГК точно в парковое состояние.

Для СГК по схеме 2-SPE разгон гиророторов и приведение к парковому состоянию на рис. 2 b выполняется аналогичным способом. Здесь линия b₁ , ортогональная центральной линии а 1 первой пары, параллельна оси O y g , а линия b ₂ параллельна оси Oz g системы координат СГК O x cg y cg z cg .

ВКЛЮЧЕНИЕ КЛАСТЕРА ГД В КОНТУР УПРАВЛЕНИЯ

После дискретной фильтрации значений f углового рассогласования вектор 8k применяется в цифровом законе управления СГК gk+1 = Bgk + Сек;  т k = Kg к + Рек;

М 8 = tok х G ° + J (С 8 p + [С: to p x]tok + тД к       к       к           к к        к к      к       к где Gk = Jtok + Hk. Далее вектор потребного цифрового управления СГК Mgk с помощью явного закона распределения команд между шестью ГД «пересчитывается» в столбец uк = {ufk } сигналов управления ГД, которые фиксируются на полуинтервалах цифрового управления СГК с периодом Tu для формирования управляющего момента Mgk(t) (2), детали представлены в [11].

РЕЗУЛЬТАТЫ ИМИТАЦИИ сой m = 1000 кг и тензором инерции J = diag{812; 587; 910} кг м2 на солнечно-синхронной орбите (ССО) высотой 720 км. Пусть при широтно-импульсном управлении с периодом TU = 4 с каждый из восьми РД в составе ДУ имеет максимальное значение тяги Pm = 0.5 Н, а каждый из шести ГД в составе СГК имеет модуль собственного КМ hg = 100 Нмс и период цифрового управления Tu =1 0.25 с. Будем считать, что к моменту времени t = ti = 7000 с завершен режим успокоения КА, с помощью БИНС определяются ориентация КА и его расположение в ИСК, а также положение Солнца, и на интервале времени t е [7000,7600] с выполняется угловая стабилизация КА в ИСК при широтноимпульсном управлении двигательной установкой. Закон углового наведения КА на интервале времени t е[ tip, tf ] = [7600,8548] с для совмещения нормали к панелям СБ с направлением на Солнце при итоговом развороте корпуса КА вокруг оси Эйлера на угол ф* =76.6 град представлен на рис. 4. Здесь приведены программные значения компонентов векторов углового

При компьютерной имитации рассматривался информационный спутник с мас-

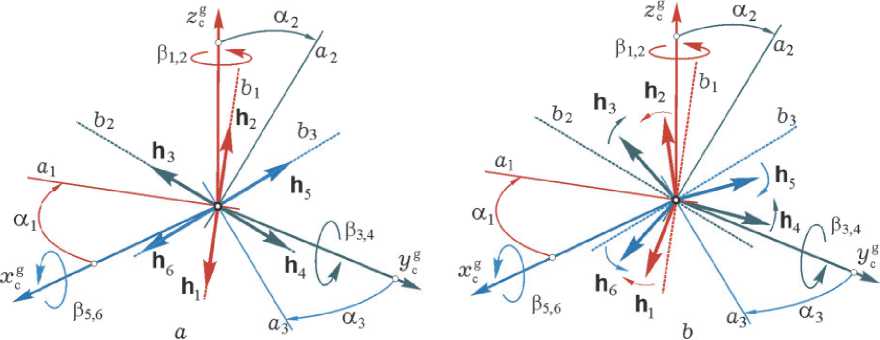
Рис. 3. Разгон роторов в 3 парах ГД ( a ) и приведение СГК схемы 3-SPE в парковое состояние ( b )

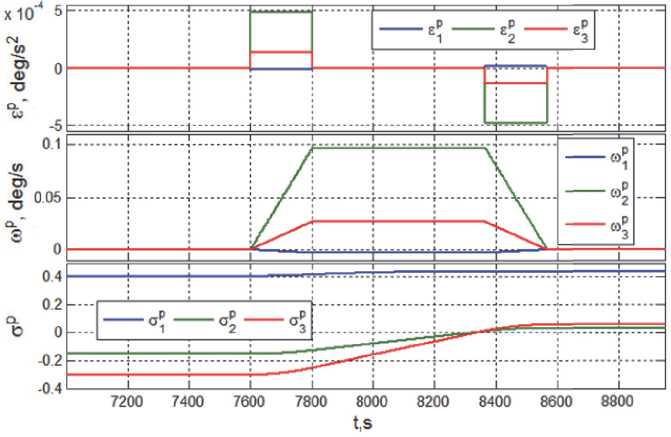
Рис. 4. Начальное положение и программное угловое движение КА при наведении панелей СБ на Солнце

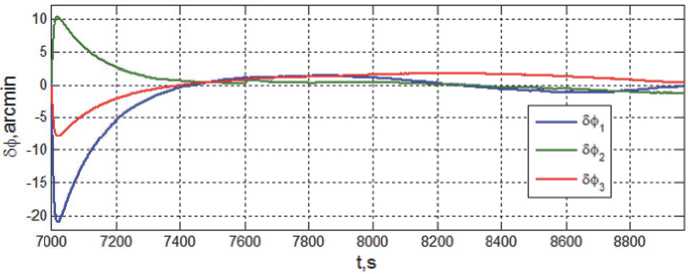
Рис. 5. Ошибки стабилизации начального положения и движения КА при наведении панелей СБ на Солнце

ускорения ε ^p ( t ) и угловой скорости ω ^p ( t ) , а также компонентов вектора модифицированных параметров Родрига σ ^p ( t ) . Достигаемые при этом ошибки стабилизации движения КА приведены на рис. 5.

В момент времени t = t _f ^p = 8548 с начинается длительный режим угловой стабилизации КА с панелями СБ, ориентированными на Солнце. Здесь на интервале времени t ∈ [8548, 14428] с попарно разгоняются роторы шести ГД без возникновения реактивных возмущающих моментов от этих гиророторов при стабилизации углового положение корпуса спутника в ИСК с помощью широтно-импульсного управления ДУ. В момент времени t = 14428 с положение векторов КМ с модулями h _g = 100 Нмс в парах ГД определяется углами β ^o _{2 i - 1} = 45 град и β ^o _{2 i} = –135 град, i = 1 ÷ 3 .

При значении параметра ρ = 0.65 и парковом состоянии СГК по схеме 3-SPE углы β _p ГД имеют значения β ^* _{2 i - 1} = 15.661816459787 град, β ^* _{2 i} = - 105.661816459787 град, i = 1 ÷ 3 , что приводит к симметричным значениям углов a i = -45 град и 5 i = 60.661816459787 град для ножничных пар.

На интервале времени t ∈ [14428, 14488] с все шесть ГД разворачиваются в соответствующих направлениях с одинаковыми постоянными угловыми скоростями, что дает соблюдение условий Н (t) = 0 и Mg (t) ≡ 0 . В результате углы β p ГД принимают значения βˆ2i-1 = 14.661816459787 град, Ргi =-104.661816459787 град, г = 1 ^ 3, которые сохраняются до момента времени t = 14528 с, когда включается закон настройки СГК с условием Mg ≡ 0 . В течение 20 секунд на интервале времени t ∈ [14528, 14548] с указанный закон настройки приводит СГК точно в парковое состояние.

Начиная с момента времени t = 14548 с широтно-импульсное управление двигательной установки отключается и в контур угловой стабилизации спутника в ИСК включается СГК с цифровым управлением. Следует отметить, что структуры законов широтно-импульсного управления ДУ (5) и цифрового управления СГК (6) близки, но аналитические соотношения для расчета диагональных элементов матриц K , B , C и P существенно отличаются.

Изменения углов β _p нечетных ГД ( p = 1,3,5) при завершении приведения СГК в парк и включении его в контур управления представлены на рис. 6, а углов β _p четных ГД ( p = 2,4,6) – на рис. 7.

Ошибки стабилизации КА в ИСК по углам 5ф i и угловым скоростям 5w i на интервале времени t ∈ [14548, 14648] с при включении СГК в контур цифрового управления приведены на рис. 8.

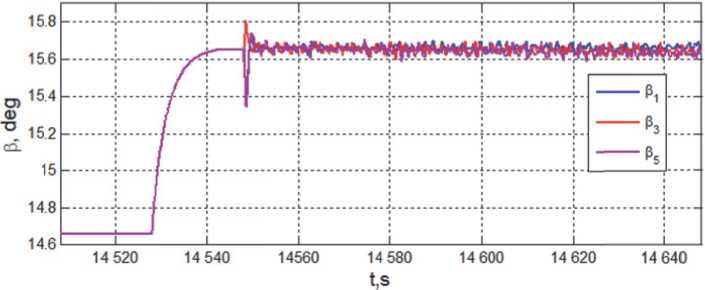
Рис. 6. Углы ГД при завершении приведения СГК в парк и включении его в контур управления

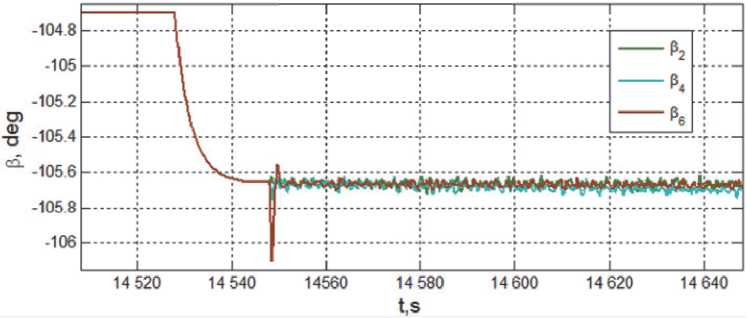
Рис. 7. Углы ГД при завершении приведения СГК в парк и включении его в контур управления

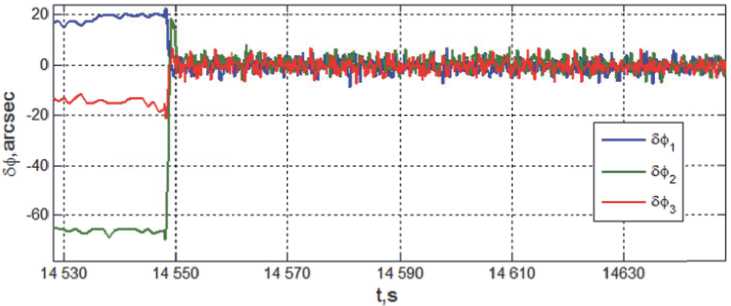
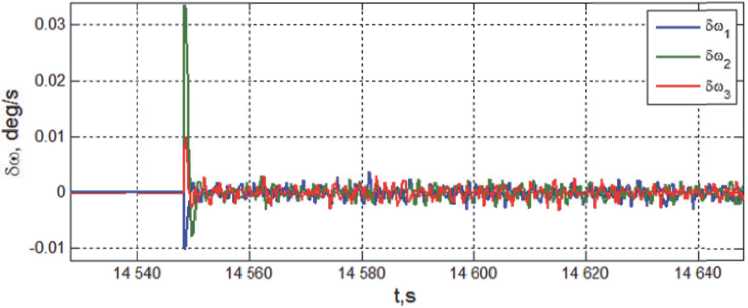
Рис. 8. Ошибки угловой стабилизации КА при включении СГК в контур управления

ЗАКЛЮЧЕНИЕ

Разработан новый метод разгона (увеличения скоростей вращения) роторов гироди-нов и приведения силовых гироскопических кластеров (СГК) двух кратных схем в парковое состояние без создания инерционных и гироскопических возмущающих моментов при угловой стабилизации корпуса спутника в ИСК с помощью двигательной установки. В этом методе учитывается ограниченность энергетических ресурсов системы электропитания КА в начале его миссии, гиророторы разгоняются до номинального значения их собственного КМ последовательно по парам ГД. При этом возникает большая длительность разгона роторов всех гиродинов (несколько часов) при угловой стабилизации КА с панелями СБ, ориентированными на Солнце. Отсутствие возмущающих моментов в процессе такой инициализации СГК приводит к экономичности работы ДУ в отношении расхода топлива при длительной угловой стабилизации КА в ИСК.

Представлены методика определения парковых состояний СГК обеих схем при явных законах их настройки, разработанные алгоритмы углового наведения и управления ориентацией КА с помощью ДУ при переводе ориентации спутника в такое состояние, при котором нормаль к плоскости панелей СБ направлена на Солнце. Приведены результаты компьютерной имитации динамических процессов при включении СГК в контур цифрового управления ориентацией спутника.