Различные формы записи уравнений движения и граничных условий новой теории оболочек
Автор: Никабадзе М.У.
Статья в выпуске: 7, 1999 года.
Бесплатный доступ
В работе представлены различные формы записи уравнений движения и граничных условий новой теории оболочек.
Короткий адрес: https://sciup.org/146211217
IDR: 146211217 | УДК: 539.3
Текст научной статьи Различные формы записи уравнений движения и граничных условий новой теории оболочек
Уравнения движения новой теории оболочек (НТО) для любой среды, как известно
|
[1], имеют вид |
(_) . ) Ik ° 3 k (") k <_’ k V I M + T + X - W , (1) ( + ) (+’ Ik " 3 k ( o ) k <+’ k V I M - T + X - W . |
Здесь V - -ст o -оператор ковариантной производной [2]. g
Легко усмотреть, что компоненты тензоров внутренних усилий [1] представляются следующим образом:
) Ik 7 °) o I »JkL з\ , 3
M =\ngTP 1 _ x) dx -
0 J
= h 1 f(l - x3)У I + x3f joIjoM- У 111 PJk (l - x^dx h \ 1 x g т x g Tg +, g Г P 1 x dx о J ( J M JJ
,'’ Ik ’/) o I "Jk 3,3
M -\ng tP x dx -
0 J
o
° 3 k 7~’ o 3 » nk ° 3 к
t -\пд^Р -Q
0 n
• - h 0 1 - x 3 ) J rj
i
o
o
o
o
V
M
Mt
o
- gJ
PJ x3 dx 3,
o o з *+; m g ;„m M
k
;
o o 1(-) o
Q3 k-jnP3 kdx’
o 7_ ) o 3 k 3
где
o
( _ ) o ( _ ) _ 1 o o ( - ) ( - ) I o ( _ ) _ 1 1 ij o K o L n 4gg g 33 - h & ’ & - ggg - 2 s s KL g I g J
U 3V , 3^ 3\ “I 1(3Y(m’
gJ~ & s s jp g m ~& 1 - x’gJ+x V gJgiM”gj) ’
( _ ) k (+) k ( - ) k ( + ) k
-
Заметим, что X и X представляют собой компоненты внешних сил, W и W компоненты инерционных сил, а Pn - а° -компоненты тензора напряжений Пиола.
g
Соответствующие уравнениям (1) граничные условия, например, имеют следующий вид [1]:
(-) ) (-й (-’ (-) (-)(
M v I = S на Y 1 ; и = и о на Y i ,
|
(3) |
|
|
oo ( + ) Ik^-^ (+’к ( + ) ( + ) ( + ) ( + ) M vI- S на Y 1 ; и - и 0 на Y 1 - |
(-) (°-) (-’ (+) (+) (+)( где у = Yi ^ у2 и Y = Yi u Y2 — граничные контуры внутренней о^ и внешней
(+)
СУ i базовых поверхностей соответственно.
Следует заметить, что уравнения (1) и соответствующие граничные условия можно записать и в более краткой форме. В самом деле, умножая первое соотношение (1) на (1-х3), а второе на х3, и потом, складывая полученные таким образом соотношения, будем иметь oo vMIk+1 -2x3T3k+Xk=Wk, v x3^H, (4)
где введены следующие обозначения
, ojk ’ Ik з<:’ Ik ° Ik / 3V ;)Ik 3^VIk
M ( I - x ) M + xM , X 1 - x ) X + xX ,
W
Ik
о _ __ о _ __
(zXk X.-ik
W + xW
.
Проводя совершенно аналогичную процедуру, из (3) с учётом (5) получаем °,Ik° ok о °3
M Vi = S на Y1; u = ио на у2 , V x е[0,1], где oo
"k L 3V-’k 3<2k L 3 (-) 3(+) _ 3 (-)
S = 1 - x ) S + xS ’ и = 1 - x ) и + xu ’ и о = 1 - x ) и о + xu 0
0 , U-) (+) 0 , J-)(
Y , = 1 - x 3) Y , + x 3 Y , , Y 2 = 1 - x 3 ) Y 2 + x 3 Y 2 .
Заметим ещё, что при жёстком защемлении краёв будем иметь и = 0 на у , V x е [0,1] , а при свободных краях
IM I' V, .0 на Y , V x '«M . 0 , а-) ( + )
где Y = 1 - x 3 у + x 3 Y .
Представляя уравнения (1) в более развёрнутом виде, будем иметь
( - ) o ( - ) I J
VjM
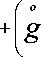
o oo
J o J I ( - ) 1 3 ” 3 j ( - ) j ( - ) J
I-g-Д m + t + x - w
( + ) o ( + ) IJ f o J o J I ( + ) I 3
VIM +l g+I-g-Д m
oo
” 3 J ( + ) J ( + ) J
T + X = W ,
oo
(-) o ( - ) I 3
VIM
o
h
- 2
o o oo f o o I (-) IK o 3 (-) 13 o 3 3 (-) 3 (-) 3 ^мд.Д M + g } M + T + X = W
| IK IK J I
oo o o oo
(+) o (+) 13 o - 2 o o I (+) IK o 3 (-) 13 o 3 3 (+) 3
VjM - h gt^-g-J M + g+ M - T + X = W IK IKI
o
(+) о( где Vo __ ^o -оператор ковариантной производной.
Аналогично из (4) получаем
< - > o o I J f o J
V,M ^VgI
o J ) o 1 3 / з\ o 3 J o J g I J M + 1 - 2 xiT + X
o J
WJ
o
(-) o o
v m
I 3
o
h
- 2
o
g
l
+ _
IJ
o o
- gIJ J M
J++g I Mr3+1 - 2 x ’)T33+;X3=W?3
Следует отметить, что в случае оболочек постоянной толщины
o3 o gj = dIn h = 0 и,
например , из (6) получаем
o
( - ) o o I J
VjM +
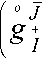
- o JI o”/13 gIJM + o g
:3Q 3J. X1-^FJ.
( - ) o °
V IM
I 3 - h
- 2
+ _
IJ
o I o
- gIJ J M
IJ
+
3 o 33
o 3 o 3
+ X - W .


