Различные представления тензора деформации Коши-Грина и линейного тензора деформаций и их компонент в новой теории оболочек

Рассматриваются две конфигурации пространства оболочки - отсчётная и актуальная. Величины, символы, компоненты тензоров, а иногда и тензоры, относящиеся к отсчётной конфигурации пространства оболочки, снабжаются нуликом сверху, а величины, символы и компоненты тензоров, относящиеся к актуальной конфигурации, пишутся без нулика [1,2,3].

Радиус-векторы произвольных точек пространства оболочки в отсчётной и актуальной конфигурациях задаются соответственно выражениями

И

/ уА А I         А 1 / \А А 1 A z           /"— *     5                         /

конфигурации [2-4].

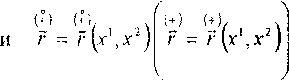
задают

базовые поверхности в отсчётной

(2) внутреннюю

(актуальной)

"              \ (т )

Вектор л(х',х2)= г(х'

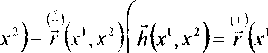
)-г\х,х") , отображающий

внутреннюю базовую поверхность о0| оу на внешнюю

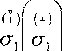
является (в общем

случае, не является) перпендикулярным к внутренней базовой поверхности <т₀ о_й [2,3].

Порождающая новую теорию оболочек новая кинематическая гипотеза заключается в следующем: точка отсчётной конфигурации пространства оболочки с радиус-вектором (1) в актуальной конфигурации займёт положение, определяемое радиус-вектором (2).

Легко усмотреть, что на основании принятой новой кинематической гипотезы параметризации как отсчётная, так и актуальная конфигурации являются новыми параметризациями [4]. В связи с этим, следовательно, соответствующие геометрические объекты этих конфигураций будут отличаться тем, что символы, входящие в геометрические объекты отсчётной конфигурации снабжаются нуликом сверху, а символы актуальной конфигурации надо писать без нулика [2,3]. Притом при выписывании геометрических объектов отсчётной конфигурации необходимо учитывать легко получаемые условия, вытекающие из перпендикулярности вектора h к внутренней базовой поверхности ой [4].

Теперь, вводя векторы перемещения внутренней и внешней базовых поверхностей соответственно соотношениями

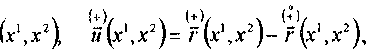
вектор перемещения произвольной точки пространства оболочки, как легко усмотреть, будет иметь вид [2]

Замечание. При изложении материала применяются обычные правила тензорного исчисления [1,5,6]. В основном остаются в силе обозначения и соглашения, принятые в ранее опубликованных работах. В частности, употребляются прописные и строчные латинские индексы. Причём прописные латинские индексы пробегают значения 1,2, а строчные - 1,2,3.

1. Тензор деформаций Коши-Грина. Как известно [1,2], этот тензор через вектор перемещения представляется в виде

6' = lfvz7 +V77 i W -V^ ~ 2k

или в оУ - ковариантных компонентах

Легко усмотреть, что на основании (3) градиент вектора перемещения представится в виде [2]

Vz7 = Г³ й- й + (1 - x³]V и + х V и ,

или вводя обозначения

- У У й -У У ° У . з\У з Й ц = и-и, ц-\и, ц = \и, ju = \l-x )).i+x ц ,

будем иметь

Vw = f Д + ^ = г ^ + \V-x y/Ax ц .

Учитывая (8) в (4), получим следующее представление тензора деформаций Коши-Грина, а именно

»    1 | Лз „    _ Лз " «_т Лч Л; _ _ Лз « -    ° - -3    °       1

^£=21^Г ^ ⁺ ^^{Г +}   ^ ^{+ Г Г ,и} ' М'М* М‘М^{г +} М‘Р у

Теперь представим (7) и (8), например, в о^ -ковариантных компонентах. Легко усмотреть, что будем иметь

Aq^^'q' Apq⁼^-»q' Йч^'^, Дря^-^ЙрЧ^Йч'          0°)

и

V, Ид = g_p P_q + P_pq = gp P_q + V ~ A" )Mpq + ^X Mpg ■

(И)

Следует заметить, что

Д^’ =0, ^=v3^o, 4=0.

Легко представить также тензор деформации Коши-Грина (9) в 4 ковариантных

компонентах. Следовательно, будем иметь

bpq

1     ° з 6     ° з о о а ° з " з А з 9 А «з о А е ?

2 gp Mq + gq Ир + Ppq + Pqp + gp gq P„ P + gp P_q„ P + gq Pp„ P + Pp_n Pq

Заметим, что (13) можно было получить также подстановкой (11) в (5).

Легко усмотреть, что из (13) с учётом (12) получаем е 1      »        6 А, е

⁶PQ ⁼ ^ MpQ ⁺ MqP ⁺ Нр. PQn >

рз

1      6        6       ⁶ Al

— — рР + рРЗ + рРт р ,

1       6       6 S

•т

Следует отметить, что тензор деформаций Коши-Грина можно ещё представить в

следующем виде:

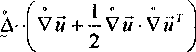
о        £ /   °         О 1                                                                                                                            °         О О с э где А = - Ся + С;„   - единичный тензор четвёртого ранга [б], а Си-rnlrnfmгп и

С„_; -f_nEr” - изотропные тензоры четвёртого ранга [1], Е- единичный тензор второго

ранга [1,6].

Учитывая (8) в (15), легко получаем

1 /

°. Дз — ^r 1 Дд Дт — — Дз о _ о _ Дз ⁰ »т А" г ца рА-\г г ц-рА-r р-рл-ц-цг А-ц-р^г

Легко усмотреть, что в сг^ -компонентах (16) с учётом (12) представится в виде

6           1 f °       ° / ⁰ 3 I ⁹ 1 ( ° К ' I ^л 1 ° К \ ^й

^, = - gp gq + gp gq A + ~ gp gq ’ gp gq И» ⁺

1   03036 о з s ft, o,§ ft         6

+ - gpgqMnP gpPqnP ^gqPpnP ^PpnPq-

Теперь выразим

характеристики a^

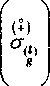
компоненты тензора деформаций Коши-Грина через

- параметризации. С этой целью вспомним, что связь между

и суТ -компонентами и ковариантными производными от компонент любого

тензора, ранг которого не меньше единицы, осуществляется посредством компонент переноса единичного тензора второго ранга (ЕТВР) [2,4]. В частности, имеют место

следующие соотношения

сохраняющие силу при любых перемещениях свободных

и глухих индексов, за

исключением свободного индекса р~р = р при операторах ковариантных производных.

Следует отметить, что

V,

и V,

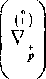
- операторы ковариантных производных при

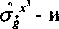
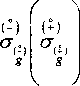
- параметризациях соответственно

Легко усмотреть, что

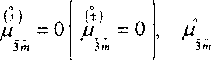
и, следовательно, на основании соотношений второй строки (18) с учётом (19) опять получаем (12).

Далее для сокращения письма компоненты тензора деформаций Коши-Грина будем

(-)                                                     _ выражать только через ст. -характеристики. Из контекста будет видно, что они через g

(?)                        с

а_(Ъ -характеристики будут выражаться аналогично.

Легко заметить, что на основании (18), например, (5) и (17) соответственно представляются в виде

6        1 ( ° т ° п ° m° лi         °      1        °         "

s = — К В + В- в IV И- + — V . и V- w рч 21        ⁹         " р I ^{т ,$} 2 ^{р т} ч

£ = — В- В + В- В* U 1 В^М V + В U + Pq   2 ' ^^Г- 6'i о Р у к 2 I ° ^р oq ' Од 6р Л'мк

+ - \gpggPhP g'pPqnP + ВдМрЯР + РрЙРд.

Из последнего соотношения (20) в свою очередь получаем

-       * *М ⁰ к 'М ’I •      * ° “л

⁶Р«  Д ^’ 8у ⁺Ку В к у^мк + yMp_h Рд. ’

4з "- ^/4 + Лз + Л« Л

6        1 ( о ^v И

•^33 2Лз + Л„ /'

2 v             /

Следует отметить, что для выражения компонент тензора деформаций Коши-Грина

посредством <т_(Ъ -характеристик надо воспользоваться помещёнными в круглые скобки 8

соотношениями (18).

2. Линейный тензор деформаций. Представления линейного тензора деформаций и его компонент легко получим из приведённых выше соответствующих представлений тензора деформаций Коши-Грина и его компонент, если в них будем пренебрегать произведениями геометрических характеристик, В самом деле, обозначая линейный

тензор деформаций через е, например, из (4), (9) и (16) получаем соответственно

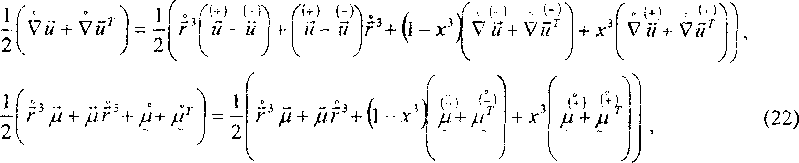
? = Д-- г ЦА- /LI

Заметим, что при написании первой строки (22) было учтено соотношение (6), а -последних двух строк (22) - последнее соотношение (7).

Аналогично, обозначая компоненты линейного тензора деформаций через е,

например, из (17), второго соотношения (20) и (21) получаем соответственно

е,ч

JI

6     1 f ⁰ К ° I ⁰ 1 ⁰ К I e

^-\gpgq^gpgq \Цкь

И

е РЧ

1 I ⁰ i ⁰ £ ^с з ° £ I о 1 I °м ^с к *м Ч = -\gpg_q+gqgp\M_k + -\g^ g_q+gq gp

^Мк

= 2 \^% ⁺ ^8р Ai,

Мк ’

4з = j^P A + А з j , 4 = A

Далее не представляет большого труда доказать, что

°        11 Ч 1 ,   3 ' ’ Wo 0      °    ”        0      7-1

^kl'v ^x УкУ* ^.^K^ut-^W\ gn-g*, ^Л -

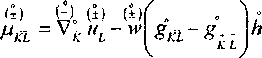
MK =g Мкю Mx =g ^^ Mf.^^p. Pp=h Vp, Из=Ь w-w

V_P = ll-x W_P + x Vp =d_Pw+u g -g_t- A , Vp=dpW-v-u g_ -g, \h , I PK PK J                        I PK PK )

где

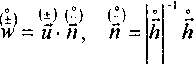
- h з\(-), з(Д . Л зУ°), зб) .   _ У ик= (1 - х )и^ + х и^ w-\l-x)w+xw, w = un.

av'p-a. - оператор ковариантной производной [3].

Теперь на основании третьей и пятой формул третьей строки (24) компоненты (23) можно еще представить в более подходящем новой теории оболочек виде. Имеем

⁶            ° К ⁰ L ° К ⁹ Г о И ° К 3     ⁰ к ° 3 j

Уе = 2^ ^ge '"^g6 ^gpУ^"'' ^{8e + g}e ^gPj^h^'y

У (-) w- w

^c>3^Tl gpHk^Wp L e₃₃^h ²V         )

Следует заметить, что в отличие от названий, принятых в [2,4,5,7], gPq> gp. gPq, gp> gp,' g4^ g4-   называются компонентами переноса ETBP. Причем p p g^g^ gp^g;

р

называются основными компонентами переноса ЕТВР, если в качестве

основной взята внутренняя (внешняя) базовая поверхность.

Теперь рассмотрим оболочки класса TS (тонкие и пологие) [7]. В этом случае, как легко усмотреть, будем иметь gu ^gu^

g

и, например, (25) представится в виде ePQ — Д gp gg* gg gp 1/Дг+7^ gp 8q +Sq gp y^K'

4з = 2 ht. + gph w-w +hig,, , e33 = h w- w

Если оболочка имеет постоянную толщину I/? = const , то gp = x³d_plnA = 0 и из

(25) получаем

6 1

е,

= 2 Й /4+ ^hWp L e₃₃= h w- w

Наконец, рассмотрим оболочки случае, например, из (26) получаем класса TS, имеющие постоянную толщину. В этом

- h w-w

6        1 °r ° L ° К ^y Г о ⁶

^ерд "Tl gp gg ⁺ gg gp р^т, ^егз