Разложение аналитической функции в ряд Лорана

Пусть f(x) является голоморфной функцией, в кольце г < |х — а| <  R, где О < г <  R < со . Тогда функцию f(x) можно однозначно представить в виде сходящегося ряда в данном кольце:

/(х) = 2-_ cn(x - ay = 2” О сп (X - ay + 2”=1 ^, (1), где ау – это произвольная окружность \ц - а\ = р,г < р < R направленная против часовой стрелки.

Доказательство: f(x) – является голоморфной внутри кругового кольца, граница которого представляет собой две окружности K и k имеющие общий центр в точке а (радиуса R и r).

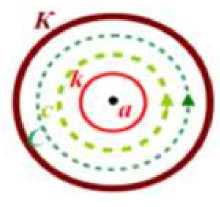
рис 1.

Образуем ряд, который располагается по положительным и отрицательным степеням х — а , и сходящимся к функции f(x) в каждой точке x, которая лежит внутри кольца, то есть при условии г < |х — а\ = р < R.

Для этого возьмем два радиуса т! и R! так, чтобы т < т' < р < R' < R, и обозначим через c и C окружности данных радиусов с центром в точке a. По условию, функция f(x) будет являться голоморфной в кольце между данными окружностями, включая и сами окружности c и C. Исходя из формулы Коши для сложного контура имеем:

л ¹ Г №№^ 1 Г fW

2тп Jc ц — х 2ти ц — х или

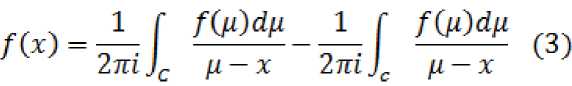
где x – это точка находящаяся между c и C, а пути интегрирования проходятся в положительном направлении.

Заметим, что в первом интеграле формулы (3) Д – является точкой окружности C, получим

1           1         V (х — а)^п

• У~х (^__а)(1-^—^ ZL^-ay*¹

Данный ряд (4) сходится равномерно для любых точек д находящихся на |х-а Р / л окружности L , потому что имеем И      1 .

Также, во втором интеграле формулы (3) /Л является точкой окружности С, заметив что имеем:                                  (5)

Ц-Х     (х-а)1--—         (х-а)^{п+1 х} '

Исходя из этого, получаем ряд, который равномерно сходится для всех точек д-а

-< 1

Р

• У- лежащих на окружности с , так как

Подставляя разложения (4) и (5) в интегралы формулы (1), и выполнив почленное интегрирование (это возможно вследствие равномерной сходимости относительно у), получим:

fto-2n=o27ri/c

fUXx-a)ⁿ (ji— a)ⁿ⁺¹

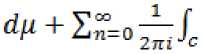
ЛдХдуа)^ (х—a)n+1

^Д (6)

Положим С, =TT,L ^ -1 <- ⁼ 0:1:2...) ⁽⁷⁾

■: = — I /(.г/х^-^:;’-^ - = 1.2.3    (8).

Перепишем (6) в виде f (т j = Z^V -_:; 'Л ^_ -0 - Z<=: Зу 'Л ^_ -0 '

Формулы (7) и (8) можно объединить -: = 777 I. —^у^-— (п=0,1,2,...,...,-1,-

• 2,...)    (10), где контур интегрирования у является произвольной

окружностью с центром в точке =?, которая лежит внутри данного кольца.

Действительно, так как подынтегральные функции формул (7) и (8) являются голоморфными всюду внутри данного кольца, то, не изменяя значений -у. и д_:., можно принять в них в качестве, пути интегрирования любую окружность у с центром в точке а, которая лежит внутри данного кольца.

С другой стороны, ь”=™4 №№-^п-1

1 f f(~X)dp

— J ;—^т; = ^с-п (п = 1,2,3,...). 2Л1     (д-a) ⁷¹⁺¹       ” ⁴       , , /   7

Исходя из этого следует то, что коэффициенты , которые определяются формулой (10), не зависят от точки x , так как под у можно понимать любую окружность с центром в точке , которая лежит внутри данного кольца.

Исходя из этого, (9) можно записать в виде (1). Таким образом получим изображение функции f(.xj, которое справедливо для всех точек х, находящихся внутри данного кольца. С помощью ряда (1), который состоит из двух частей: первая его часть, , является рядом расположенным по возрастающим x-a, вторая часть – это ряд, который расположен по убывающим отрицательным степеням x-a

(степенной относительно

)

. Данные два ряда сходятся в каждой точке x,

которая лежит внутри данного кольца. Ряд (1) называют рядом Лорана.