Разложение заданных характеристик методом наименьших квадратов по системе неортогональных функций

ства X функции из F оказываются неортогональными, даже если они являются ортогональными как непрерывные или заданные на некоторой специальной сетке. Поэтому применение МНК приводит к решению очень больших систем линейных уравнений, что далеко не всегда удаётся выполнить с требуемым качеством. В ряде работ предлагается введение специальной сетки отсчётов, на которой функции F являются орто-нормированными, например, выборочные, сферические и двумерные тригонометрические функции. Но тогда приходится интерполировать измерения характеристики H(x) в точки этой специальной сетки, что вносит дополнительные погрешности в модель уже в самом начале.

Для облегчения применения МНК можно сначала ортонормировать систему функций F , то есть получить систему функций Ф = { ф 1 ( x ), ф ₂ ( x ), ..., ф _т ( x )} таких, что их скалярное произведение

( фф ) = Е Ф i ^{( x ф ( x} ) = ⁵ j = * a i _ j ’ (2) x s X L 0’ i ^ ^j .

При этом возможно, что система F линейно зависима, тогда m <  M . Функции ф линейно выражаются через F , то есть Ф будет ортонор-мированным базисом линейного пространства векторов (в данном случае – функций), натянутого на F . Процедура Грама-Шмидта решает задачу ортогонализации системы векторов в случае линейно независимой системы F [1]:

Ух = / 1 , y 2 =

( / 1 / 1 ) / 1 ( / 2 / 1 ) / 2

У 3 =

(/. /. ) (/2 f. ) (/3 /1 )

( /. / 2 ) /. ( / 2 / 2 ) / 2 ( / 3 / 2 ) / 3

фк(x)    П------\ I)

V⁽ У к У к ) Vг-1Г ’      ^(}

Г о = 1 , Г к = Г ( f „..., f_k ) =

( f 1 f 1 ) ( f 2 f . )

( f 1 f k ) ( f 2 f k )

– (5)

вим (6-7) в виде

^t = a k 1 ^Ф 1 + a k 2 ^Ф 2 + ... + a k,k- 1 ^Ф 1 - 1 + a kk f k ^{. (9)}

Тогда

( fd 1 )

( f k f k )

определители Грама. При этом, если потребовать, чтобы ф _к ( x ) выражалась через f 1 ( x ), ..., f_k ( x ) , то решение (3-5) является единственным.

Если система функций h ₁ ( x ), ..., h_k ( x ) является линейно зависимой, то Г ( h ₁,..., h_k ) = 0 . Поэтому, если Г ₁ - 1 ^ 0 и Г _k = 0 , то в процедуре (3-5) функцию f_k ( x ) следует удалить, так как она линейно зависима от предыдущих функций f

1 ( x ) , f 2 ( xf-, fk - 1 ( x ) . Если при этом f_k ( x ) тождественно не равна 0 (а тождественно равных нулю функций в F быть не должно), то из ( У к / к ) = Г _k = 0 следует y_k ( x ) = 0 , что также является признаком линейной зависимости f_k ( x ) от предыдущих функций.

При большем количестве M функций в множестве F процедура (3-5) становится громоздкой и может давать неточные результаты, так как требует вычисления определителей высоких порядков. Применим модифицированный вариант этой процедуры ортонормирования. Преобразуем процедуру следующим образом. Будем представлять очередную функцию ф ₁ ( x ) в виде разложения по f_k ( x ) и уже найденным Ф 1 ^{( x} Л Ф 2 ^{( x} ^" Ф - 1 ^{( x} ) :

zk (x )= fk (x ) - ( ЛФ1 )Ф1 (x ) -

¹ - ⁽ fk Ф 2 ^Ф 2 ^{( x} ) - - - ⁽ fk Фk - 1 К - 1 ^{( x} ) - ⁽⁶⁾

Ф1 (x )= z^xL =

V(zkzk )=_________________Ук(x)_________________

V (fkfk ) - (/^ )2 - (ЛФ2 )2 -...-(/kфk -1 )2

В силу единственности системы функций ф процедуры (3-5) и (6-7) дают одни и те же функции ф , а функции y_k ( x ) и z_k ( x ) могут отличаться только постоянным множителем. Поэтому, если z_k ( x ) = 0 (или подкоренное выражение в (7) равно нулю), то f_k ( x ) нужно исключить из рассмотрения.

Отметим, что процедура (6-7) не требует вычисления определителей больших порядков, как это имеет место в (3-5). Однако получаемые функции в (6-7) не выражены в явном виде через функции F . При необходимости к этому представлению

^Ф 1 = c k 1 f l + c k 2 ^f 2 + ... + c kk f k        ⁽⁸⁾

можно вернуться следующим образом. Предста-

c kp    a kp c pp + a k , p + 1 c p + 1, p ⁺ a k , p + 2 c p + 2, p ^{+ .}"

... ⁺ a k , k - 1 c k - 1, p

f k - I

2 a k C p , i = p

a_kk ,

i <  p <  ^k - 1, (10) p = k .

Или в матричном виде:

(c ck, ck, ck,3

K ckk -1

I c kk J

' a ^{k 1}

a_{k 2}

a_{k 2}

a_{k 3}

a_{k 3}

a_{k 3}

• •    • akk - 1

• •    • akk - 1

• •    • akk - 1

K

• •    • akk - 1

K 0

0"

K

¹ J

c k - 1,1

c k - 1,2

c k - 1,3

c k - 1, k - 1

V a kk J

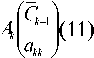
Приведём в качестве иллюстрации построение модели мегарельефа Луны в виде конечного отрезка двумерного ряда Фурье

L

H ( 9 , d ) « a 0 ⁺ 2 co ^{s( w 6} ) ^{[ a}mn co ^s( n ² ) ⁺ b mn ^si n ⁽ nf >^] m , n = 1

(12) по данным каталога ULCN 2005 [2], содержащего 272931 точек. Из этого каталога выбиралось множество S из 7736 опорных точек, приблизительно равномерно распределённых по поверхности, и для них описанным способом строились модели (12) с различными порядками L . При возрастании порядка модели (12) СКО её погрешности на множестве S уменьшалось до нуля. Однако СКО на всём каталоге достигало минимума 4.78км при L =17, а затем начинало возрастать, так как при повышении порядка в модель вводятся высокочастотные гармоники, несвойственные рельефу Луны. Это является обычной ситуацией при построении моделей: на опорных точках она может быть хорошей, но неудачной в целом. Отметим, что применение стандартных пакетов программ (например, АСНИ “СФЕРА” [3], SHTOOLS [4]) для построения модели непосредственно методом наименьших квадратов на S оказалось безуспешным из-за вычислительных погрешностей при решении систем линейных уравнений высоких порядков.