Размерные эффекты и топологические особенности наномодифицированных композитов

В.А. СМИРНОВ и др. Размерные эффекты и топологические особенности наномодифицированных композитов дной из важнейших задач технологии наномодифицированных композитов, возникающих на этапе поисковых исследований, является нахождение размеров частиц и концентрационных границ содержания наноразмерного модификатора.

Высокая стоимость большинства наномодифицирующих добавок является лимитирующим фактором для выполнения эмпирических исследований. По этой причине последние должны предваряться теоретическими исследованиями и математическим моделированием.

Существует ряд моделей, в рамках которых оказывается возможным сделать предварительные оценки искомых параметров. В настоящей работе анализируются модели, обращающиеся к размерным и топологическим особенностям дисперсной системы.

Размерные эффекты оказывают влияние на реологические свойства и характерные значения поверхностной энергии системы. Важность анализа размерных эффектов определяется тем обстоятельством, что известные закономерности изменения макроскопических свойств часто не выполняются для систем, образованных структурными единицами малых размеров (число атомов структурной единицы сравнимо с числом атомов на ее поверхности). Именно по этой причине на практике наблюдается аномальное изменение физических свойств тонкодисперсных материалов.

При рассмотрении агрегативной устойчивости в дисперсных системах предложено выражение [1]

где γ ~10 (безразмерный коэффициент), k – постоянная Больцмана, T – абсолютная температура, a – размер структурной единицы.

Выражение (1) имеет размерность поверхностного натяжения и фактически представляет собой характерную энергию теплового движения, отнесенную к поверхности структурной единицы. Отмечается [1], что самопроизвольное диспергирование становится возможным (микроге-терогенная система термодинамически устойчива), если (1) превыша-

В.А. СМИРНОВ и др. Размерные эффекты и топологические особенности наномодифицированных композитов ет поверхностную энергию (σ12~0,01...0,1 Дж/м2) в системе (энергетический выигрыш от участия частицы в тепловом движении превышает затраты энергии при увеличении площади межфазной границы).

Наличие в числителе выражения (1) постоянной Больцмана предопределяет оценку для размера структурной единицы – а~10–9 м. Эта величина может быть принята как нижняя граница, определяющая наноразмерный модификатор: для материала, образованного такими частицами, существенны размерные эффекты.

Известна [2] зависимость вязкости системы, образованной моноди-сперсными частицами, от приложенного напряжения:

1 z³ _ кткТ z³

3 z ch z - sh z ka1 z ch z - sh z где z = λa2P/kT, λ – среднее расстояние между равновесными положениями структурной (кинетической) единицы, a – размер структурной единицы, P – механическое напряжение, κ~1, τ – среднее время нахождения структурной единицы в положении равновесия (τ ≠ τ(a)).

Для авторов [2] наибольший интерес представляла зависимость η = η ( P ) вязкости от механического напряжения. Соответственно, в работе [2] приводится подробный анализ поведения второго множителя

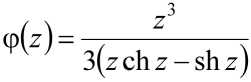
в правой части (2). В области определения функция (3) монотонно убывает, асимптотически приближаясь к нулю (рис. 1). При этом максимальное значение limq)(z) = 1 – соответствующее наибольшей вязкости дисперсной системы – достигается в стационарной точке (3):

б/ф 1 z2 3zchz-3shz-z2 shz

hm — = - hm —^— ----------z = 0

^->+o dz 3 -—>+o       (z ch z - sh z)

На зависимость η = η ( a ) вязкости от размера структурной единицы, помимо множителя (3), оказывает влияние множитель η₀ = 3 κτ kT/ λ a² . Подобно зависимости (3), зависимость

hM

OcaP3 VkT^y

(ka-P , kaP

-----ch----- kT kT

, ka'P

-sh---- kT

В.А. СМИРНОВ и др. Размерные эффекты и топологические особенности наномодифицированных композитов

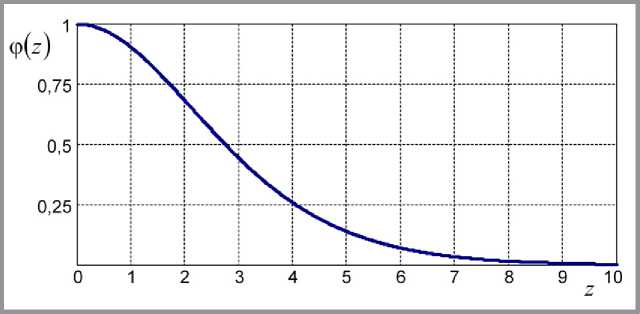
Рис. 1. Относительное изменение вязкости дисперсной системы при механическом воздействии

монотонно убывает (рис. 2), но при a → +0 она терпит разрыв II рода:

lim r|(a) = +oo ,                                                                 (6)

a->+0

г ^П lim —- = a^+o da

lim и—^+0

2тХ2й3/)3| 2ma2Pch kT

O . л 2 4 r>2 'Xi- ka P

Ik i Aka P Isn----

'                 7 kT

к T ka Pen--kT sh---- kT        kT

Соотношения (6) и (7) свидетельствуют, что зависимость (2) может являться моделью реологических свойств дисперсной системы, лишь

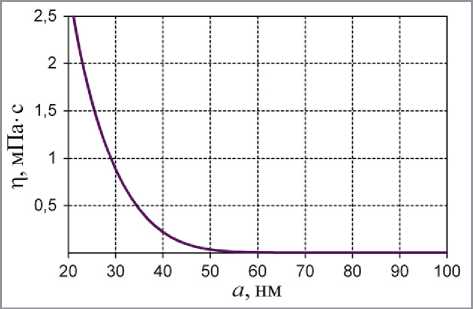
Рис. 2. Зависимость вязкости системы от размера частиц дисперсной фазы: τ = 1 мкс, T = 300 ^oК, λ = 10 нм, P = 1 кПа

В.А. СМИРНОВ и др. Размерные эффекты и топологические особенности наномодифицированных композитов начиная с некоторого характерного размера частиц дисперсной фазы; при a→+∞ малое отклонение ∆a размера частиц соответствует существенному изменению вязкости системы.

В качестве характерного размера естественно принять значение, соответствующее точке наибольшей кривизны (2):

,

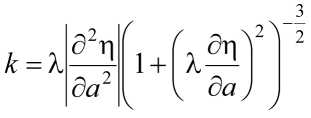
где λ – нормирующий множитель (после умножения на который, в частности, второе слагаемое в скобках становится безразмерным), равный

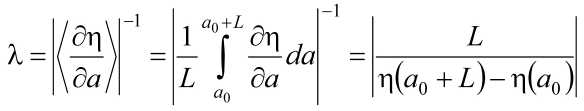
Знак нормирующего множителя произволен и не оказывает влияния на значение (8). Для выбранных параметров системы (рис. 2) нормирующий множитель равен

X = 2,83-10"5 Па 1

Зависимость (8), построенная с учетом (10), изображена на рис. 3.

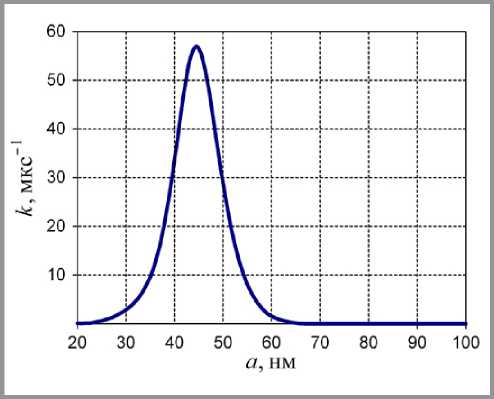
Рис. 3. Коэффициент кривизны зависимости вязкости системы от размера частиц ((5), рис. 2)

В.А. СМИРНОВ и др. Размерные эффекты и топологические особенности наномодифицированных композитов

Абсцисса точки экстремума (8) может быть найдена численно:

ak ,max = 43,7 нм.                                                   (11)

Найденная оценка согласуется с результатом, полученным в работе [3] из наиболее общих соображений (относительная доля поверхностных атомов частицы дисперсной фазы).

Таким образом, диапазон диаметров частиц, соответствующий проявлению размерных эффектов в дисперсной системе, оказывается равным 1~ a ~45 нм. Нижняя граница диапазона соответствует атомным кластерам (для фуллерена a ≤ 2 нм); верхняя – таким материалам, как аэросил (a ∈ [5; 40] нм) и технический углерод (a ∈ [10; 100] нм).

Наряду с задачей нахождения размерного диапазона, внимание многих ученых привлекает исследование топологических особенностей нанокомпозитов.

Известно, что оценки структурных показателей многофазных материалов могут быть получены на основе представлений о топологии перколяционной сетки. При переходе к системе, дисперсная фаза которой представляет собой короткие волокна (хаотическое армирование), анализ топологических особенностей существенно усложняется.

Так, известна [3] модель дисперсного армирования, в основе которой – предположение о размещении волокон в некоторой плоскости. Выводы (касающиеся объемной доли дисперсной фазы), полученные при использовании этой модели, находятся в согласии с результатами экспериментов (для систем, наполняемых волокнами асбеста). В то же время, предложенная в [3] модель фактически не учитывает два существенных обстоятельства:

• •    взаимные расположения центров волокон пространственно некор-релированы: они лишь распределены по закону равномерной плотности, а не находятся в ячейках плоской гексагональной решетки;

• •    дополнительная степень свободы при переходе к пространственной системе может нарушить протекание, имеющее место для двумерной решетки; для восстановления протекания потребуется увеличить объемное содержание дисперсной фазы.

Ценность предложенной [3] модели состоит в том, что она может быть источником соображений, увеличивающих вычислительную эффективность алгоритмов численного моделирования перколяции по решетке, образованной короткими волокнами.

В.А. СМИРНОВ и др. Размерные эффекты и топологические особенности наномодифицированных композитов

Следует также отметить, что определение количества наномодификатора возможно в рамках различных моделей микроструктуры композита.

В частности, можно принять, что все распределенные в объеме дисперсионной среды структурные единицы модификатора имеют линейную конформацию. Тогда определение концентрации сводится к решению задачи протекания по перколяционному каркасу (кластеру), образованному одномерными объектами длины l (здесь «одномерность» понимается как условие lm >> dm ). В другой модели микроструктуры помимо линейной конформации предполагается то, что структурные единицы наномодификатора привиты к поверхности частиц наполнителя (диаметр частиц df>> lm ). Очевидно, что в этом случае перколяционный кластер будет реализован только при выполнении условия A f < 2 lm , (где A f — зазор между частицами наполнителя) и дополнительной реализации протекания по сферам диаметром df + lm . Решение последней задачи известно; интерес представляет решение первой.

Не останавливаясь подробно на алгоритме и его реализации^*, обратимся к результатам стохастического моделирования протекания по перколяционной решетке, образованной распределенными (по закону равномерной плотности) в представительном объеме (куб с ребром l = 2 мкм) волокнами дисперсной фазы.

Моделирование выполнено для волокон диаметром d_f = 2 и 10 нм, длина волокон составляла l_f = 100 и 200 нм (вычислительный эксперимент в соответствии с планом 2²). Для каждой точки плана эксперимента найдено количество контактов между волокнами при числе волокон от 100 до 100 000 (логарифмическая шкала, 9 точек).

Зависимости относительного числа контактов (частное от деления числа контактов на число волокон) от объемного содержания дисперсной фазы для двух точек плана эксперимента приведены на рис. 4 и 5.

Как следует из рис. 4 и 5, существует практически линейная взаимосвязь между объемной долей дисперсной фазы и относительным числом контактов между волокнами.

Сопоставление рис. 4 и 5 также свидетельствует о том, что при равной объемной степени наполнения реализация пространственной пер-

В.А. СМИРНОВ и др. Размерные эффекты и топологические особенности наномодифицированных композитов

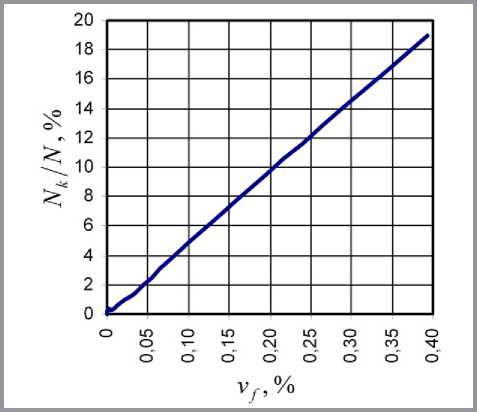
Рис. 4. Относительное число контактов: l_f = 100 нм, d_f = 2 нм

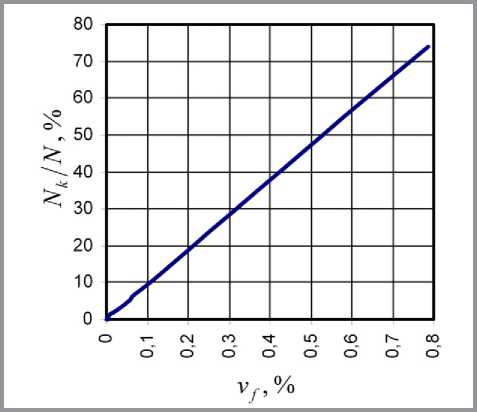
Рис. 5. Относительное число контактов: l_f = 200 нм, d_f = 2 нм

коляционной решетки возможна при введении волокон с увеличенным коэффициентом формы.

Тангенсы углов наклона прямых, аппроксимирующих четыре зависимости N_k ( ν _f )/ N ( ν _f ) (две из которых приведены на рис. 4 и 5), определяют прогнозы порога перколяции ν _f,crit – значения объемной степени наполнения, соответствующие равным числам контактов и частиц дисперсной фазы (см. таблицу).

По значениям таблицы построена неполная квадратичная модель (кодовое выражение):

v_/crit = 0,0468 - 0,015^ + 0,0312x₂ - 0,0 Цх₂, x_z g [-1;1], z = 5 .          (12)

Прогнозы порогов перколяции в исследованных системах

X1 ( lf ), нм	X2 ( df ), нм
	2	10
100	0,0207	0,103
200	0,0106	0,053

Свободный член ν _f,crit,0 ≈ 5 % определяет среднее значение, при котором в рассматриваемой системе реализуется протекание по волокнам

В.А. СМИРНОВ и др. Размерные эффекты и топологические особенности наномодифицированных композитов наномодификатора. Отметим, что найденное значение существенно меньше, нежели известное νf,crit,0 = 16 % для порога протекания по решетке из сфер. Таким образом, значение νf,crit,0 = 16 % не имеет универсального характера.

Знак параметра b₁ = –0,015 модели (12) указывает на то, что с увеличением длины волокна (x₁ → max) объемная доля, соответствующая протеканию, становится меньше. Это, очевидно, обусловлено увеличением вероятности контакта при увеличении длины волокна. Отметим также, что при постоянном объеме волокна увеличение его длины сопровождается сокращением поперечного размера (x₁ → min). При этом негативное (положительное по знаку) влияние третьего слагаемого (12) уменьшается.

Линии уровня модели (12) приведены на рис. 6.

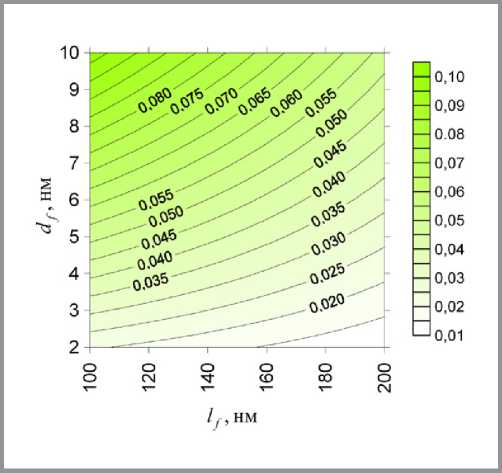
Рис. 6. Линии уровня порога протекания по волокнам наномодификатора

Вид линий уровня свидетельствует, что в исследованной области оптимальные условия для протекания реализуются при l_f = 200 нм, d_f = 2 нм. Результат визуализации указанной системы в процессе стохастического моделирования (при ν _f = 8•10^–4 – существенно ниже порога перколяции) представлен на рис. 7.

В целом следует подчеркнуть, что использование наноразмерных объектов с высоким коэффициентом формы позволяет сформировать

В.А. СМИРНОВ и др. Размерные эффекты и топологические особенности наномодифицированных композитов

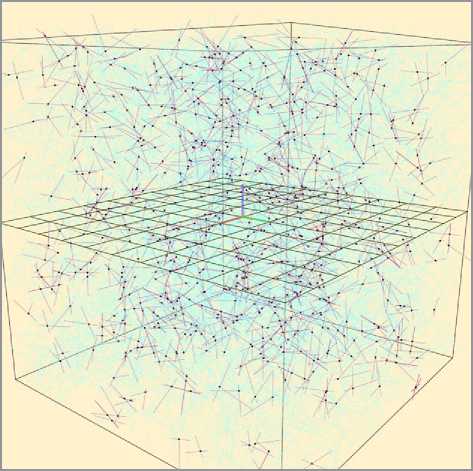
Рис. 7. Моделирование протекания по волокнам

(темный тон – волокна, которые войдут в состав перколяционной решетки; светлый тон – изолированные для текущей объемной доли волокна;

точки – контакты волокон)

перколяционный каркас (при условии равномерного распределения) при сравнительно малом содержании объектов.

Отметим также, что предложенный и реализованный алгоритм стохастического моделирования распределения наноразмерных объектов (с учетом их геометрических характеристик и объемного содержания) планируется использовать при исследовании систем, образованных частицами сложной формы.

В.А. СМИРНОВ и др. Размерные эффекты и топологические особенности наномодифицированных композитов

Уважаемые коллеги!

При использовании материала данной статьи просим делать библиографическую ссылку на неё:

Смирнов В.А., Королев Е.В., Альбакасов А.И. Размерные эффекты и топологические особенности наномодифицированных композитов // Нанотехнологии в строительстве: научный Интернет-журнал. М.: ЦНТ «НаноСтроительство». 2011, Том 3, № 4. C. 17–27. URL: (дата обращения: ______________).

Dear colleagues!

The reference to this paper has the following citation format:

Smirnov V. A., Korolev E. V., Albakasov A. I. Size effects and topological characteristics of nanomodified composites. Nanotechnologies in Construction: A Scientific Internet-Journal, Moscow, CNT «NanoStroitelstvo». 2011, Vol. 3, no. 4, pp. 17–27. Available at: (Accessed __ ___________). (In Russian).