Размерный эффект усиления для дисперсно-наполненных полимерных нанокомпозитов

DOI:

Как известно [7], в случае дисперсно-наполненных полимерных нанокомпозитов принято полагать, что уменьшение размеров дисперсных наночастиц приводит к сильному увеличению их степени усиления Ен/Ем (где Ен и Ем – соответственно модуль упругости нанокомпозита и матричного полимера). Однако так же хорошо известно [3], что уменьшение размеров частиц нанонаполнителя интенсифицирует процесс их агрегации, что в конечном итоге резко повышает эффективный размер нанонаполнителя в полимерной матрице. Так, авторы

работы [3] показали, что параметр агрегации k ( r ) зависит от удельной поверхности S_u исходных наночастиц следующим образом:

k ( p ) = 7,5 x 10 - 3 S u ,              (1)

где S_u дается в м²/г.

В свою очередь, величина S_u зависит от диаметра наночастиц D _ч согласно уравнению [6]:

S u =

6 ρ н D ч ^,

где р н - плотность нанонаполнителя.

Поэтому возникает вопрос, какой нанонаполнитель эффективнее с практической точки зрения – имеющий малые размеры исходных частиц, но сильно агрегирующийся, или имеющий относительно большие размеры наночастиц, но слабо агрегирующийся. Целью настоящей работы является ответ на поставленный выше вопрос, для чего были использованы два дисперсно-наполненных полимерных нанокомпозита, имеющие одинаковую полимерную матрицу, но наполненные дисперсным наполнителем, чьи размеры исходных частиц различались примерно в 15 раз.

Эксперимент

В качестве матричного полимера использован полипропилен (ПП) промышленного производства марки «Каплен» 01 030 со средневесовой молекулярной массой (2-3) x 10⁵ и индексом полидисперсности 4,5. В качестве нанонаполнителя применялись: наноразмерный карбонат кальция (СаСО₃) в виде компаунда марки Nan-Cal P-1014 (производство Китай) с размером частиц 80 нм и массовым содержанием 1–7 масс. % и глобулярный наноугле-род (ГНУ) (производство группы компаний «Объединенные системы», г. Москва, Российская Федерация) с размером частиц 5–6 нм, удельной поверхностью 1400 м²/г и массовым содержанием 0,25–3,0 масс. %.

Нанокомпозиты ПП/СаСО3 и ПП/ГНУ получены смешиванием компонентов в расплаве на двухшнековом экструдере Thermo Haake модели Reomex RTW 25/42, производ- ство ФРГ. Смешивание выполнено при температуре 463–503 К и скорости вращения шнека 50 об/мин в течение 5 минут. Образцы для испытаний получены методом литья под давлением на литьевой машине Test Sample Molding Apparate RR/TS MP фирмы Ray-Ran (Великобритания) при температуре 483 К и давлении 43 МПа.

Механические испытания на одноосное растяжение выполнены на образцах в форме двухсторонней лопатки с размерами согласно ГОСТ 112 62-80. Испытания проводили на универсальной испытательной машине Gotech Testing Machine CT-TCS 2000, производство Тайвань, при температуре 293 К и скорости деформации ~2 x 10^-3 с^-1.

Результаты и обсуждение

Исследовать влияние размера исходных частиц нанонаполнителя на степень усиления Е _н/ Е _м полимерных нанокомпозитов можно с помощью двух теоретических моделей: перколяционной и молекулярной [5]. Первая из указанных моделей оперирует следующим уравнением [5]:

Е н = 1 + 11 ( ф н Cb а Г,

Е м                  ,

где ф - объемное содержание нанонаполнителя; с -коэффициент пропорциональности между ф н и относительной долей межфазных областей; b _а - безразмерный параметр, характеризующий уровень межфазной адгезии нанонаполнитель – полимерная матрица.

Величина ф _н определяется из хорошо известного уравнения [5]:

Ф н

W н ρ н ,

где W _н – массовое содержание нанонаполнителя; р _н - его плотность, оцениваемая в случае наночастиц следующим образом [5]:

р_н = 188 ( D ч ) ^1/3, кг/м³ ,              ⁽⁵⁾

где D _ч – диаметр исходных частиц нанонаполнителя, который дается в нм.

Величина с принята равной 1,05 для дисперсных наночастиц [5], а параметр bа сни- жается по мере роста фн, что обусловлено агрегацией нанонаполнителя: для нанокомпозитов ПП/ГНУ в интервале 9,20–1,50 и для ПП/СаСО3 – в интервале 2,60–0,80. В дальнейшем для простоты оценок было принято: для нанокомпозитов ПП/ГНУ Ь а = const =1,50 и для ПП/СаСО3 - Ьа = const = 1,0.

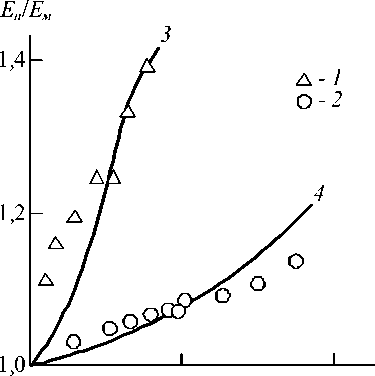
На рисунке 1 приведено сравнение экспериментальных и рассчитанных согласно уравнению (3), то есть перколяционной модели, величин степени усиления Е _н/ Е _м для рассматриваемых нанокомпозитов. Как можно видеть, получено достаточно хорошее соответствие теории и эксперимента: их среднее расхождение составляет 8 % для нанокомпозитов ПП/ГНУ и 2,5 % – для ПП/СаСО₃. Основной вклад в указанное расхождение вносит принятое выше допущение Ь _а = const.

Молекулярная модель использует для определения степени усиления дисперсно-наполненных нанокомпозитов следующее уравнение [5]:

1 = LC

1 ст t0'~'' да,

где l ₀ – длина скелетной связи основной цепи, равная 0,154 нм для ПП [4]; С _да - характеристическое отношение, которое является показателем статистической гибкости полимерной цепи [2] и может быть рассчитано из уравнения [4]:

2 d

С =              + -,

” d ( d - 1 ) ( d - d_f ) 3

где d_f – фрактальная размерность структуры нанокомпозита; d – размерность евклидова пространства, в котором рассматривается фрактал (очевидно, в нашем случае d = 3).

Размерность d_f определяется следующим образом [1]:

d f = ( d - 1 )( 1 + v ),                 (9)

где v - коэффициент Пуассона, оцениваемый по результатам механических испытаний с помощью следующего соотношения [5]:

Е н = 1 + 0,1 9 ^ _н l _С т Ь а

Е          D 1/2

мч

о_Т _ 1 - 2v

Е н = 6 ( 1 + V ) ,

где l _ст – длина статистического сегмента цепи полимерной матрицы.

где О Т и Е _н - соответственно предел текучести и модуль упругости нанокомпозита.

Величина l _ст определяется следующим образом [4]:

Значения параметра Ь _а приняты такими же, как и ранее. На рисунке 2 приведено срав-

^{0             4             8} W н , масс. %

Рис. 1. Зависимости степени усиления Е _н/ Е _м от массового содержания нанонаполнителя W _н для нанокомпозитов ПП/ГНУ ( 1 , 3 ) и ПП/СаСО₃ ( 2 , 4 ):

1 , 2 – экспериментальные данные; 3 , 4 – расчет согласно уравнению (3)

нение экспериментальных и рассчитанных согласно уравнению (6) значений степени усиления Е _н / Е _м для рассматриваемых нанокомпозитов. Как следует из этого сравнения, вновь получено достаточно хорошее соответствие экспериментальных данных и расчетов согласно молекулярной концепции усиления – их среднее расхождение составляет 7,5 % для нанокомпозитов ПП/ГНУ и 1,0 % – для ПП/СаСО₃.

Следовательно, изложенные выше оценки предполагают, что основным фактором в определении степени усиления дисперсно-наполненных полимерных нанокомпозитов является размер исходных частиц нанонаполните- ля [в уравнении (3) он определяет основную характеристику нанокомпозита – объемное содержание нанонаполнителя]. Тем не менее агрегация частиц нанонаполнителя также играет существенную (и отрицательную) роль – ее усиление по мере роста ϕн, обнаруженное для всех классов нанокомпозитов [6], снижает уровень межфазной адгезии, характеризуемый параметром bα, и уменьшает тем самым степень усиления нанокомпозитов [см. уравнения (3) и (6)]. Снижение уровня межфазной адгезии также зависит от размера исходных наночастиц. Так, введение 3 масс. % нанонаполнителя снижает величину bα в 6 раз для

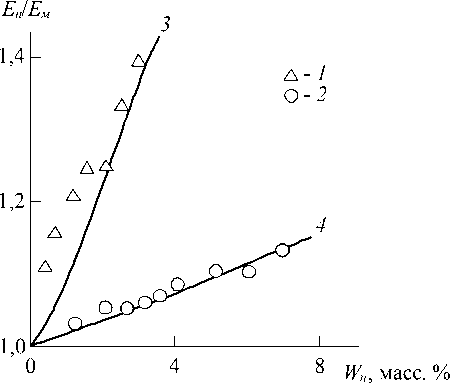
Рис. 2. Зависимости степени усиления Е _н/ Е _м от массового содержания нанонаполнителя W _н для нанокомпозитов ПП/ГНУ ( 1 , 3 ) и ПП/СаСО₃ ( 2 , 4 ):

1 , 2 – экспериментальные данные; 3 , 4 – расчет согласно уравнению (6)

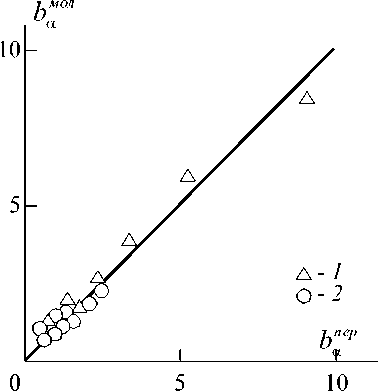
Рис. 3. Сравнение значений параметра b _α , рассчитанных согласно уравнениям (3) ( b _α ^пер) и (6) ( b _α ^мол) для нанокомпозитов ПП/ГНУ ( 1 ) и ПП/СаСО₃ ( 2 )

нанокомпозитов ПП/ГНУ и только в 2 раза – для ПП/СаСО3.

И в заключение рассмотрим один важный аспект использованных выше моделей усиления дисперсно-наполненных полимерных нанокомпозитов. Обе указанные модели включают параметр b _α , характеризующий уровень межфазной адгезии, который может быть рассчитан согласно экспериментальным значениям Е _н/ Е _м из уравнений (3) ( b _α ^пер ) и (6) ( b _α ^мол ). На рисунке 3 приведено сравнение параметров b _α ^пер и b _α ^мол , которое показало их достаточно хорошее соответствие (среднее расхождение b _α ^пер и b _α ^мол составляет ~11 %).

Таким образом, несмотря на различные критерии вывода указанных уравнений [6], их разную функциональную форму, параметр b _α , рассчитанный согласно упомянутым выше моделям, имеет практически одинаковые абсолютные величины. Это обстоятельство подтверждает физическую реальность указанной характеристики и возможность ее использования при описании структуры и свойств полимерных нанокомпозитов [5].

Выводы

Следовательно, результаты настоящей работы показали влияние двух конкурирующих факторов (размера исходных частиц нанонаполнителя и уровня их агрегации) на степень усиления дисперсно-наполненных полимерных нанокомпозитов, причем влияние первого из указанных факторов превалирует. Улучшение свойств полимерных нанокомпозитов с практической точки зрения может быть достигнуто как уменьшением размера исходных частиц нанонаполнителя, так и подавлением процесса их агрегации.