Размеры атомов и ионов, сила ковалентной связи между ними в молекулах и кристаллах
Бесплатный доступ
Короткий адрес: https://sciup.org/149128888
IDR: 149128888
Текст статьи Размеры атомов и ионов, сила ковалентной связи между ними в молекулах и кристаллах
Проблема размеров и форм атомов, составляющих вещество, по-прежнему привлекает внимание многих специалистов [1—11]. За более чем 80-летнюю историю изучения кристаллических структур создано много систем радиусов атомов и ионов. Их можно подразделить на две главные группы: системы аддитивных и неаддитивных радиусов.
Cyммa аддитивных радиусов равна или очень близка к величине расстояния между соответствующими атомами в химическом соединении. Такие радиусы фактически являются частями межатомных расстояний. С развитием прецизионного рентгеноструктурного анализа и квантово-химических методов расчета стало принято считать, что границу между атомами следует проводить по минимуму электронной плотности (ЭП) [1—3, 7, 10].
Неаддитивные радиусы — это радиусы свободных атомов или ионов, получаемые путем квантово-химического расчета радиального распределения ЭП. Среди них широко известны орбитальные радиусы максимумов ЭП, вычисленные Дж. Вебером и Дж. Кромером путем решения уравнения Дирака. Предложено несколько критериев, которые позволили бы приписать каждому атому свой размер вне этих максимумов: а) по одинаковой величине ЭП [4], б) по фиксированной доле (скажем, 98 %) полной ЭП [8], в) по значению расстояния, на котором экранированный псевдопотенциал обращается в нуль [11] или химический потенциал электронного облака равен электростатическому потенциалу [5, 9]. Получаемые таким образом радиусы удовлетворительно коррелируются со свойствами атомов и ионов и даже с некоторыми характеристиками их взаимодействия в молекулах и твердых телах. Однако они слабо связаны с межатомными расстояниями.
Исходя из квантово-механического описания межатомных взаимодействий в терминах молекулярных орбиталей, даже представленных линейной комбинацией атомных орбиталей, трудно представить, что распределение ЭП в молекуле или кристалле равно или близко к сумме ЭП свободных атомов, вследствие интерференции волновых функций. С точки зрения функционала ЭП, это также не очевидно.
Тем не менее в результате эмпирического анализа параметров взаимодействия в молекулах щелочных галогенидов обнаружилось, что оно может быть описано как перекрывание сферических ионов [6]. При этом величина ковалентной энергии пропорциональна глубине перекрывания, которая определяется разностью d R между суммой предполагаемых радиусов и экспериментальным значением межатомного расстояния [6]. Радиусы катионов оказались близки по величине к рассчитанным квантово-механически для значения ЭП = exp (‒4.3), то есть 0.014 ат. ед. (0.09 электронов на кубический ангстрем) радиусам свобод-
^ 800
^ 600
s
9 400
Q 200
0 20406080100120140
dR (пм)
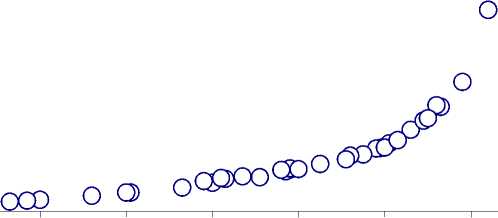
Pиc. 1. Зависимость энергии диссоциации молекул от глубины перекрывания ЭП атомов
ных катионов [4]. В то же время определенные по методу перекрывания сфер радиусы анионов от фтора до йода превосходят на 0…40 пм соответствующие расчетные значения, что, по-видимому, обусловлено диффузностью валентных орбиталей анионов.
Чтобы проверить целесообразность и достоверность представления ковалентного взаимодействия в форме перекрывания сферических свободных атомов, мною была предпринята попытка подобрать их размеры так, чтобы за- висимость энергии диссоциации двухатомных молекул от глубины перекрывания атомов описывалась плавной кривой, а изменение радиусов в пределах каждого периода таблицы Менделеева следовало, в общем, обратному порядку первых потенциалов ионизации элементов. Данные о межатомных расстояниях Rm и энергиях диссоциации молекул D0 были взяты из справочника С. С. Бацанова [1].
Результаты для ряда гомоядерных молекул представлены на рис. 1 и в табл. 1, где также приведены значения радиусов свободных ионов [4], исправленные по методу перекрывания сфер [6]. График зависимости D 0 (d R ) на рис. 1 может быть описан плавной кривой при малом разбросе значений. Из анализа табл. 1 следует, что вычисленные таким образом величины атомных радиусов изменяются в соответствии с Периодической системой элементов Менделеева.
Отмечаются следующие очевидные или не противоречащие периодическому изменению соотношения между зарядом ядра и электронным строением атома закономерности:
-
• Радиусы атомов возрастают с ростом номера периода, но начиная с четвертого периода это возрастание слабое.
-
• В рядах s - и p -элементов радиусы уменьшаются от щелочных металлов к галогенам. Это сокращение атомных размеров невелико и гораздо меньше, чем полагается в других известных системах.

Атомные ᴎ ионные радиусы некоторых элементов, ᴨᴍ
Таблица 1
H 92
Li 160
Li+ 69
Be 144?
Be2+ 57
В 129
B3+
C 121
C4+
N 117
n5+
О 116
О2- 140
F 106
F" 119
Na 170
Na+ 95
Mg 160
Mg2+ 86
Al 165
Al3+ 78
Si 163
Si4+ 73
P 151
p5+
S 149
s2-
Cl 145
СГ 169
К 206
K+ 128
Ca 190
Ca2+ 115
Sc 140
Sc3+
Ti 126
Ti4+ 103
V 136
v5+
Cr 115
Mn 120
Fe 121
Fe2+ 110
Cu 150
Co 140
Zn 150
Ni 148
Ga 759
Ge 163
As 158
Se 160
Br 152
Br" 185
Rb 217
Rb+ 141
Sr 200
Sr2+ 130
¥ 165
Zr 161
Nb 150
Mo 150
Tc 140
Ag 160
Au 166
Cd 155
In 176
Sn 176
Sb 167
Те 174
I 165
Г 209
Cs 239
Cs+ 158
Ba 225
Ba2+ 146
La
Hf
Ta
W
Re
-
• Радиусы атомов галогенов больше радиусов ионов следующих за ними щелочных металлов, а разница в размерах атомов и анионов галогенов возрастает от фтора к йоду. Радиусы ионов щелочных и щелочно-земельных металлов меньше атомных радиусов в среднем на 70 пм, радиусы анионов больше на 10— 40 пм. Радиус щелочно-земельного иона лишь немного меньше радиуса иона щелочного металла из того же ряда и заметно больше радиуса иона щелочного металла из предыдущего ряда (R Ca2+ > R Na+ ).
-
• Радиусы атомов d -элементов в четвертом периоде заметно ниже, чем р -элементов в том же и третьем периодах. Это вполне соответствует заполнению электронами внутренней подоболочки при возрастании заряда ядра. Более того, полученные радиусы служат индикатором осуществления химической связи в молекулах переходных элементов путем перекрывания внутрен-
- них d-орбиталей, оставляя неподелен-ной внешнюю пару s-электронов.
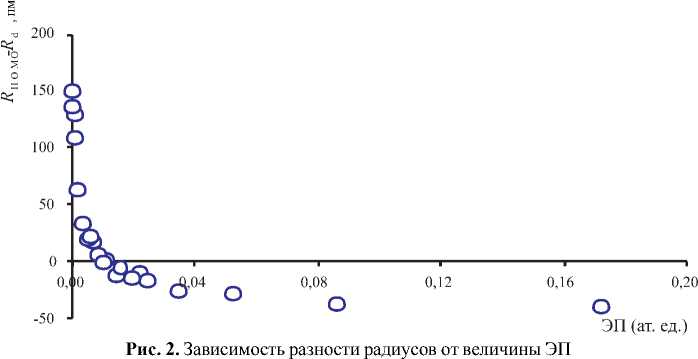
При сопоставлении полученных величин атомных радиусов с рассчитанными методом функционала плотности орбитальными радиусами RHOMO, определяемыми из условия равенства химического и электростатического потенциалов [5], обнаружилось их совпадение именно на отметке 0.01 ат. ед. ЭП (рис. 2). При этом расхождение между сравниваемыми значениями растет в области больших значений ЭП (0.01— 0.20 ат. ед.), где ее изменение круче, го- раздо меньше, чем в области «хвостов» (0.0100 — 0.0002 ат. ед.). Для построения этого графика использовались значения атомных радиусов s- и p-элементов. Они, как и радиусы ряда ионов, выделены жирным шрифтом для обозначения проверенных в свободном и связанном состояниях элементов. График, представленный на рис. 2, можно использовать для приближенного опре- деления радиуса атома, исходя из расчетных данных Т. Ганти и С. Гош [5]. Таким путем вычислены радиусы щелочно-земельных атомов, которые не образуют молекул А2, и других элементов, по которым отсутствуют экспериментальные данные. В табл. 1 они выделены курсивом. Следует заметить, что точность расчета радиусов переходных элементов ниже, чем s- и p- элементов.
На основании обнаруженного совпадения между размерами атомов в свободном и связанном состояниях можно сделать вывод о том, что образование ковалентной связи в гомоядер-ных молекулах есть результат перекрывания (взаимопроникновения) валентных ЭП свободных атомов. Это утверждение согласуется с предположением Дж. Слейтера о том, что ЭП связанной системы мало отличается от суперпозиции ЭП свободных атомов. В каждой точке области перекрывания величина ЭП, вероятно, не равна сумме ЭП свободных атомов, а форма области перекрывания не совпадает точно с формой перекрывающихся шаров, однако в итоге получается, что эти отличия несущественны. На основе полученных результатов можно избрать значение ЭП = 0.01 ат. ед. в качестве границы атомов. Оно отделяет области крутого изменения и хвостов ЭП. Точность определения радиуса составляет примерно 5 пм, потому что пологость убывания ЭП для такого низкого ее уровня можно принять равной у всех атомов и ионов, за исключением, может быть, анионов.

Таблица 2
Глубины перекрывания d R , заряды Q и размеры ионов R i в ионных и ионно-ковалентных минералах
|
Минерал |
R M-X , пм |
d R , пм |
Q , e |
R c , пм |
R a , пм |
V m |
|
Виллиомит NaF |
231 |
- 16 |
- 1.0 |
95 |
119 |
14.85 |
|
Флюорит CaF2 |
237 |
- 3 |
- 1.0 |
115 |
119 |
12.27 |
|
Na 2 O |
241 |
- 6 |
- 2.0 |
95 |
140 |
|
|
Известь CaO |
241 |
15 |
- 1.9 |
118 |
138 |
16.76 |
|
Периклаз MgO |
211 |
15 |
- 1.9 |
88 |
138 |
11.24 |
|
Корунд Al2O3 |
191 ± 6 |
45 |
- 1.5 |
110 |
130 |
8.42 |
|
Эсколаит Cr2O3 |
199 ± 3 |
50 |
- 1.5 |
120 |
130 |
9.70 |
|
Рутил TiO 2 |
196 |
45 |
- 1.5 |
120 |
130 |
9.40 |
|
Кварц SiO2 |
161 |
65 |
- 1.2 |
110 |
125 |
11.35 |
|
Перовскит CaTiO3 |
255 ± 10; 192 |
- 10; 50 |
- 1.45; +2 |
115; 125 |
128 |
11.22 |
|
Волластонит CaSiO3 |
240 ± 20; 162 ± 3 |
0; 65 |
- 1.2; +2 |
115; 110 |
125 |
13.31 |
|
Кальцит CaCO3 |
231; 138 |
4; 80 |
- 0.95; +2 |
115; 95 |
120 |
12.30 |
|
Арагонит CaCO 3 |
252 ± 10; 128 |
- 20; 90 |
- 0.9; +2 |
115; 100 |
118 |
11.40 |
|
Шпинель MgAl2O4 |
192; 193 |
31; 42 |
- 1.55; +1.6 |
95; 105 |
130 |
9.93 |
|
Магнезиохромит MgCr2O4 |
198; 199 |
27; 50 |
- 1.55; +1.7 |
95; 120 |
130 |
10.89 |
Полученные мною результаты позволяют утверждать, что решена проблема соотношения размеров свободных атомов и атомов в молекулах. Это утверждение можно распространить и на атомы в кристаллах, несмотря на то, что здесь теряется однозначность между глубиной перекрывания и силой ковалентной связи вследствие увеличения КЧ. Это дает возможность проводить анализ межатомного взаимодействия в связанных системах и, что особенно важно, сравнивать одну систему с другой на основе экспериментальных данных о межатомных расстояниях и симметрии системы и характеристиках свободных атомов (ионов).
Предлагаемый метод перекрывающихся сфер является простым, грубым, но физически корректным способом оценки размеров и зарядов ионов в соединении на базе полученных размеров свободных атомов и ионов. В табл. 2 на примере некоторых минералов приведены расчетные значения глубины перекрывания, зарядов и размеров ионов в ряду от щелочных галогенидов до карбонатов. Основные черты изменения зарядов и размеров ионов заключаются в уменьшении заряда кислорода от ‒1.9 до ‒0.9 и радиуса — от 138 до 118 пм в ряду от извести до арагонита. Заряды и размеры низковалентных ионов остаются практически неизменными, за исключением иона магния в тетраэдрической позиции шпинелидов. Обнаруживается, что ионы хрома и алюминия крупнее иона магния. Тетраэдрическая координация иона магния может быть обус- ловлена его деформацией вследствие сильного притяжения ионов кислорода ионами хрома или алюминия. Из сравнения размеров ионов и межатомных расстояний в виллиомите и извести можно сделать вывод о большом влиянии силы электростатического притяжения между ионами на величину межатомного расстояния.
На примере перовскита и волластонита, а также арагонита и кальцита показано, что плотность структуры сложных кислородных соединений определяется в первую очередь расстояниями между ионами кислорода: несмотря на большее расстояние Са—О в первых, их молярный объем в расчете на один грамм-атом кислорода ( V m) меньше.
В заключение следует отметить, что существование тесной связи между размерами свободных и связанных атомов обнаружено впервые. Приведенные в работе радиусы атомов соответствуют периодическому закону строения электронных оболочек и величине заряда ядра намного лучше, чем радиусы известных систем. Есть основания полагать, что расчет радиусов атомов и ионов по уровню ЭП 0.01 ат. ед. позволит существенно повысить уровень кристаллохимического описания и дизайна структур неорганических и органических веществ и минералов.
Список литературы Размеры атомов и ионов, сила ковалентной связи между ними в молекулах и кристаллах
- Бацанов С. С. Структурная химия. Факты и зависимости. М.: Диалог-МГУ, 2000. 292 с.
- Бейдер Р. В. Ф. Атомы в молекулах. М.: Мир, 2001.
- Рыжков М. В. Новый метод вычисления эффективных зарядов на атомах в молекулах, кластерах и твердых телах // Журнал структурной химии, 1998. Т. 39. № 6. С. 1134 - 1140.
- Butterfield C, Carlson, E. H. Ionic soft sphere parameters from Hartree-Fock-Slater calculations // J. Chem. Phys., 1972. V. 56. P. 4907-4911.
- Ghanty T K., Ghosh S. K. New scale of atomic orbital radii and its relationship with polarizability, electronegativity, other atomic properties, and bond energies of diatomic molecules // J. Phys. Chem., 1996. V. 100. P. 17429- 17433.


