Разность скоростей распространения продольной и поперечной акустических волн и параметр Грюнайзена твердых тел

Параметр Грюнайзена входит в уравнение состояния твердого тела и служит характеристикой нелинейности силы межатомного взаимодействия и ангармонизма колебаний решетки. Он вычисляется обычно из экспериментальных данных о коэффициенте объемного теплового расширения β, изотермическом модуле объемного сжатия В, молярном объеме V и молярной теплоемкости C V

β BV . γ _D

CV

Представляет интерес установление связи γ _D с другими характеристиками твердых тел [1-4]. Недавно было показано, что между параметром Грюнайзена и отношением скоростей распространения продольной ( v L ) и поперечной ( v S ) акустических волн наблюдается линейная корреляция [4]

/ = c ^f v-L- ) - c                                    (2)

γD ⁼    1              2

I vs )

где С ₁ и С ₂ – эмпирические постоянные. Эта зависимость справедлива как для кристаллических, так и для стеклообразных твердых тел [4].

Данное сообщение посвящено дальнейшему изучению корреляции (2).

В результате анализа численных значений С 1 и С 2 мы обратили внимание на совпадение этих постоянных у твердых тел одного структурного типа: С 1 ≈ С 2 . Это означает, что для таких групп тел выражение (2) принимает вид

Yd = C

Г v L

к v s

,

к v s J

где С ≈ const ≈ С 1 ≈ С 2 .

Рис. 1 подтверждает справедливость установленной зависимости (3) для 24 исследованных кристаллов. Как видно, для двух групп твердых тел в координатах соотношения (3) экспериментальные данные ложатся на две прямые, проходящие через начало координат. Здесь величина γ D рассчитана по уравнению Грюнайзена (1). Использованы данные [1].

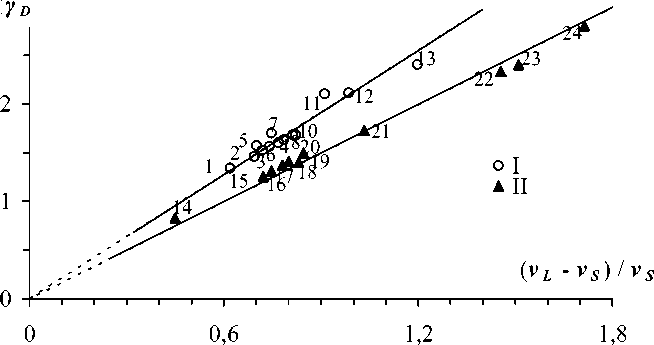
Рис. 1. Зависимость γ _D от ( v_L – v_S )/ v_S для кристаллов. Группа I: 1- LiF, 2- NaCl, 3- LiCl, 4- KCl, 5- NaF, 6- NaBr, 7- LiBr, 8- KBr, 9- Fe, 10- KI, 11- Co, 12- Al, 13- Ag; Группа II: 14 - Be, 15- Y, 16- NaNO 3 , 17- NaClO 3 , 18- Th, 19 Mg, 20- RbBr, 21- Ta, 22- AgBr, 23- Pd, 24- Au

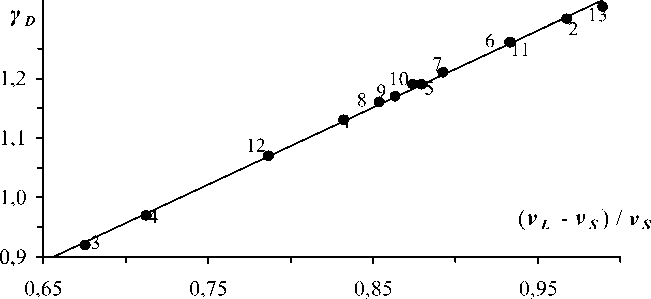
Рис. 2. Зависимость γ D от ( v L – v S ) / v S для стеклообразных (ст) и кристаллических (кр) халькогенидов. 1- GeSe (кр), 2- GeTe 1.02 (кр), 3- As 2 Se 3 (кр), 4- As 2 Te 3 (кр), 5- SbSe 3 (кр), 6- Sb 2.07 Te 3 (кр), 7- As 2 S 3 (ст), 8- As 2 Se 3 (ст), 9- As₂Se_2.03 (ст), 10- AsSe_1.22 (ст), 11- AsSe (ст), 12- Se (кр), 13- Se (ст)

Для первой группы, куда входят в основном квазиизотропные щелочногалоидные кристаллы с решеткой типа NaCl, постоянная С равна С ≈ 2, а для второй группы твердых тел – С ≈ 1,5. Названия кристаллов даны в подписи к рис. 1. Линейные зависимости γ D – ( v L – v S )/ v S получены для различных классов стекол. В качестве примера на рис. 2 приводится указанная зависимость для стеклообразных и кристаллических и халькогенидов (использованы данные [5]).

Полученная формула (3) имеет определенное практическое значение. Установив экспериментально значение С, для кристаллов, принадлежащих к определенной группе, можно определить γ D из данных о скоростях звука v L и v S . Например, параметры Грюнайзена щелочногалоидных соединений можно рассчитать по соотношению

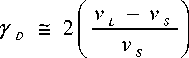
В дальнейшем требуется теоретическое обоснование установленной корреляции (3).

Работа выполнена при финансовой поддержке гранта БГУ « Лучшая научная школа »