Разновидность Фурье-инвариантных гауссовых пучков

Известно [1–5], что с помощью цилиндрической линзы можно определять топологический заряд оптического вихря. Это свойство цилиндрической линзы было замечено давно. Например, в [6] с помощью цилиндрической линзы лазерный пучок Эрмита – Гаусса с номерами (0, n ), который не несёт орбитальный угловой момент (ОУМ), был трансформирован в лазерный пучок Лагерра – Гаусса, который имеет n -кратно вырожденный ноль интенсивности и обладает ОУМ. С помощью цилиндрической линзы можно сформировать безвихревые лазерные пучки, обладающие ОУМ [7,8]. Такие пучки не имеют изолированных нулей интенсивности (сингулярных точек). Эти астигматические пучки описываются бесконечной суммой оптических вихрей с только чётными положительными и отрицательными топологическими зарядами [8].

Известно также, что линейная комбинация со сдвигом фазы на π /2 чётных и нечётных пучков Матье [9], Айнса – Гаусса [10] и Эрмита [11, 12] формирует эллиптические оптические вихри, ОУМ которых зависит от степени эллиптичности. Вклад в ОУМ у таких пучков вносит как вихревая составляющая, так и астигматическая. Причём при распространении таких эллиптических пучков вклады обеих составляющих (вихревой и астигматической) в ОУМ могут меняться [2, 13].

Измерять ОУМ оптических вихрей, в том числе дробный ОУМ [14, 15], можно не только с помощью цилиндрической линзы [1–5], но и многими другими способами, например, с помощью интерферограмм [8, 14] и треугольной апертуры [16].

В данной работе рассмотрены новые лазерные пучки, у которых объединены свойства вихревых эллипти- ческих Гауссовых пучков [9–13] и астигматических безвихревых лазерных пучков [7,8]. Такое семейство лазерных пучков мы назвали астигматическими эллиптическими Гауссовыми (АЭГ) оптическими вихрями. АЭГ-вихри в начальной плоскости представляют собой n-вырожденный ноль интенсивности с круговой симметрией, внедрённый в центр перетяжки эллиптического Гауссова пучка, радиусы перетяжки которого по декартовым осям связаны определённым соотношением, и прошедший через цилиндрическую линзу, повернутую в начальной плоскости вокруг оптической оси на угол 45 градусов по отношению к декартовым осям. Такой пучок при распространении в свободном пространстве сохраняет свою структуру с точностью до масштаба и поворота. Причём дальняя зона (Фурье-преобразование) для АЭГ-пучков отстоит от начальной плоскости на двойном фокусном расстоянии цилиндрической линзы. Рассчитан относительный полный ОУМ таких пучков. Он оказался равен алгебраической сумме двух слагаемых, одно из которых равно топологическому заряду оптического вихря, а второе пропорционально ОУМ астигматического эллиптического Гауссова пучка. Эти два слагаемых могут как усиливать, так и компенсировать друг друга вплоть до нуля. В отличие от [13], величина вкладов в ОУМ вихревой и астигматической составляющих не меняется с расстоянием.

• 1. Амплитуда пучка на двойном фокусном расстоянии от цилиндрической линзы

Рассмотрим прохождение оптического вихря с круговой симметрией и целым топологическим зарядом n, внедрённого в перетяжку эллиптического Гауссова пучка, через цилиндрическую линзу, поверну- тую в поперечной плоскости на угол а. Комплексная амплитуда такого светового поля сразу после цилиндрической линзы имеет вид:

Интеграл (4) можно вычислить:

E n ( x , У ) = w"

( x + iy ) n exp

Г r

x

w ²

У² ' w ,2

( _ _i ) ^{n +} 1

E_n ( u , v , z = 2 f ) = exp ( iu ² + iv ²)— V ² х 2 ⁿ 1 + Y 2 e²

Г ikx ² cos² a iky ² sin² a ikxy sin 2a ) exp------

I 2 f 2 f       2 f   J

2 - Y² + в² Л ² H Г ^{( 1 + в} 2 ) ^{u +} i ^{( Y} 2 ^{- 1 ) v} 1 + Y 2 e² J n [ V 1 + Y 2 eS/2 - Y² + в²

В (1) использованы следующие обозначения: ( x , y ) – декартовы координаты в поперечной плоскости при z =0, z – продольная декартовая координата, w – масштабный множитель для оптического вихря, w_x и w_y – радиусы перетяжки эллиптического Гауссова пучка по декартовым координатам, f – фокусное расстояние цилиндрической линзы, а - угол наклона оси линзы по отношению к вертикальной оси y , k =2п / X - волновое число света с длиной волны X . Комплексная амплитуда пучка (1) на расстоянии z от начальной плоскости вычисляется с помощью преобразования Френеля:

Г в² u ² + Y² v ² - 2 iuv Л exp -^r----------- .

I        1 + Y 2 e 2       J

- ^ik

^E n ⁽ u , v , z ) = —exp 2 n z

Г iku ²    ikv ² ।

I---------+--I^х ^ 2 z    2 z J

да да х J J w- n (x + iy) n exP

-да -да

Г V

x

w ²

y² ' w ,2

х exp

-

ikx ²cos²α iky ²sin²α ikxy sin 2α

-

-

2 f

2 f

2 f

х

Г ikx ²    iky¹

х exp ---- +--

I 2 z    2 z

-

ik ( xu + yv ) ] , , — ----| d x d y .

z

Если угол поворота цилиндрической линзы равен 45 градусам ( a = n /4) и расстояние после линзы равно двойному фокусному расстоянию ( z = 2 f ), то преобразование Френеля (2), с точностью до фазового множителя перед интегралами, становится преобразованием Фурье от амплитуды, описывающей оптический вихрь, внедрённый в эллиптический Гауссов пучок и прошедший цилиндрическую линзу:

- ik   Г iku   ikA — n

E ⁽ u , v , z = ² f ) = — ^e xp |—+ —| ^{w х n}               4π f 4 f 4 f

да да х J J (x + iy) n exp

-да -да

x ²    y ² ikxy ik ( xu + yv )

w x ² w y ²2 f 2 f

(3) d x d y .

Наша дальнейшая цель – вычислить интеграл в (3). Перепишем (3) в безразмерных переменных: x / w ^ x , y / w ^ y , u / w ^ u , v / w ^ v , w / w_x = Y , w / w_y = в , z 0 = 2 f , где z 0 = kw ²/2 – длина Рэлея. Тогда поле (3) примет вид:

i                                да да

E_n ( u , v , z = 2 f ) = —exp ( iu ² + iv ² ) J J ( x + iy ) n х

^П                    -да -да                  ⁽⁴⁾

х exp ( - Y² x ² - в² y ² - 2 ixy - 2 ixu - 2 iyv ) d x d y .

В (5) H n ( x ) – многочлен Эрмита. Из (5) видно, что аргумент у многочлена Эрмита комплексный. В [1] было показано, что после прохождения Гауссова оптического вихря с топологическим зарядом n и круговой симметрией через цилиндрическую линзу на двойном фокусном расстоянии за линзой на некоторой прямой в поперечной плоскости многочлен Эрмита будет иметь действительный аргумент, и, следовательно, на этой прямой будут находиться n изолированных нулей (корней многочлена). По этим нулям интенсивности можно определить топологический заряд оптического вихря. Уравнение (4) расширяет метод определения топологического заряда, предложенный в [1], на оптические вихри ( x + iy ) ⁿ , внедрённые в эллиптические Гауссовы пучки вида exp(- x²- в ² y ²). Действительно, из (5) видно, что при γ = 1 аргумент многочлена Эрмита становится действительным и на декартовой оси u будут находиться n действительных корней (нулей) многочлена.

Найдем нормированный ОУМ пучка (5). Искать ОУМ будем по известным формулам [7] (c точностью до постоянных):

т т ?да^    / ⁵ E ( x , y )

^J _z = ^Im I I ^{E ( x} ,y) I ^x ---7----

-„-„       I     ^d y

d E ( x , y ) ^Л    .

- y—;--- | d x d y , (6)

d x   J

да да

W = J J E ( x , y ) E ( x , y )d x d y ,                    (7)

-да -да

где J z – проекция на оптическую ось ОУМ, W – плотность эн е ргии (мощности) света, Im – мнимая часть числа, E – комплексно сопряжённая амплитуда к амплитуде (1). Подставляя (1) в (6) и (7), получим простое выражение для нормированного ОУМ светового поля (1):

J

— = n + i sgn w„ W^y

-

k^w x w y Sin2a P n + 1 ( ^ )       (8)

4 f     P n ( ^ ) .

При условии α = π / 4, z = z 0 =2 f , w = γ w x = β w y , вместо (8), получим ( P_mⁿ ( x ) – многочлены Лежандра):

J z = n + _i sgn ⁽ y - ^в ) P y^ ) W          eY     P n ( ^ )

1 Г в ₊ Y 2 1 Y в

Из (8) и (9) видно, что ОУМ пучка (1) состоит из двух слагаемых [2, 13]: первое слагаемое определяется вихревой составляющей пучка и равно то-

пологическому заряду вихря, а второе слагаемое определяется астигматической составляющей пучка, наведённой цилиндрической линзой и при n=0 равно ( k sin2 a ) ( w - w ^ ) (8 f Г¹ [7]. Из (8), (9) также видно, что подбором параметров эллиптичности Гауссова пучка можно скомпенсировать вихревую часть ОУМ и общий ОУМ пучка (1) будет равен нулю ( J z / W = 0) при:

Y ^{- 2} - в ^{- 2} = 2/3. (10)

ют свойством Фурье-инвариантности (с точностью до изменения масштаба и поворота на 90 градусов). Комплексную амплитуду таких АЭГ-вихрей в начальной плоскости ( z = 0) в безразмерных координатах можно записать:

E n ⁽ x , у , z = 0;^в) =

= ( x + iy ) ⁿ exp [- ( 2 + в² ) x ² - в 2 У ² - 2 ixy J .

2. Семейство астигматических эллиптических Гауссовых вихрей

Вернёмся к выражению (5). При определённой связи между параметрами эллиптичности Гауссова пучка ( у ² = р ² +2), так как ^ n H n ( a I £ ) ^ (2 a ) ⁿ при ^ ^ 0, из (5) следует, что такие вихревые астигматические эллиптические Гауссовы пучки сохраняют свою структуру в результате Фурье-преобразования:

Нормированный ОУМ АЭГ-вихрей (14) дробный, следует из (9) и равен:

А = n ₊ ^ P Uj) .

W   в#^2 P ( j )

Исходя из (14), можно получить комплексную амплитуду светового поля на любом расстоянии z и в

размерных величинах:

x exp

E n ⁽ и , V , z = ² f ) = ^f 1 +^ 2

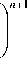
( u + iv ) n x

E n ( ^x , У , z ) = _u¹ , X ( ^{u + iv} ) n ^x z ^{( 1 +} b y )

,    , в2u2 +(в2 + 2) v2 - 2iuv iu2 + iv2--------Ц--------

+ в² )

Из (11) видно, что в Фурье-плоскости меняется масштаб, а также эллиптический Гауссов пучок и цилиндрическая линза поворачиваются на 90 градусов. В качестве конкретного примера рассмотрим такие параметры Гауссова пучка: y² = 3 и р ²= 1. Тогда интеграл (4) примет вид:

+да +да j j (x + iy)n x

-да -да x exp [-3x2 - y2 - 2ixy - 2i(ux + vy)] dx dy =     (12)

, ._xn n ,      . _xn | u ² + 3 v ² - 2 iuv ।

= ^(- i ) ₂ n ^{( u + iv} ) ^exP I-- 4-------- 1 .

И вместо (11) получим

E n ( u , v , z

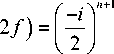
( u + iv ) n x

x exp

где

b x , У

2.-2 x exp I iu + iv

u ² + 3 v²

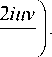
Из (11) и (13) видно, что, во-первых, при определённых параметрах эллиптичности Гауссова пучка ( y ² = P 2 + 2) на двойном фокусном расстоянии от цилиндрической линзы не возникает n -нулей интенсивности, по которым можно определить топологический заряд исходного вихря. Оптический вихрь восстанавливается и по-прежнему имеет в центре изолированный ноль интенсивности n -кратно вырожденный. А во-вторых, нами получено двухпараметрическое ( n , в) семейство АЭГ вихрей, которые облада-

—(x ² + y ²) - b u ² - b v ² + 2 iuv 2 z^V y 1 x x

kf              kf x, v = y,

^{( 1} + b y )        z ^{( 1} + b y )

4 f 1 ik ik k w2   4 f 2 z x, У

Причём радиусы перетяжки эллиптического Гауссова пучка не произвольные и должны удовлетворять соотношению

1 = 1 k W = w ⁺ 2 f'

В безразмерных переменных условие (18) эквивалентно ранее приведённому ( у = в ² + 2).

Можно показать, что световое поле, описываемое амплитудой (16), удовлетворяет параксиальному уравнению Гельмгольца:

2 ik

д д ² д ²

д z д x ² д у²

E n ( ^x , У , ^z ) = 0.

Из (16) следует выражение для комплексной амплитуды АЭГ-вихря на расстоянии z = 2 f :

/ f/

2 f ) = ( - i ) ^{n + 1} 1 + ^ f

I ^z 0 y J

- n-1 /     I \n f 1 ^ /x

x ( x + iy ) n exp

x exp <

x

kx ² + ky ² 1 + f ikxy 2 z ; y ⁺ 2 f [ ⁺ z ; ; ^J-1 7

1 + ²f

l ^z 0 y J

где z 0 y = kw y ²/2 – длина Рэлея по оси y . Если наложить ограничение на параметры Гауссова пучка и фокусное расстояние цилиндрической линзы ( z 0 y = 2 f ), то выражение (20) упростится:

^E n ( x , У , z = z

n + i

I - i | I ¹ kK I

= 2 f =—    —, — ( x + iy ) x

⁷ I 2 J ( 2^ f J ^{V 7}

x exp

4 f ⁽ x ^{2 +} y ²) - if ⁽ x ^{2 +} 3 y ² - 2 ixy )

Выражение (21) совпадает с правой частью (13) в безразмерных переменных с точностью до постоянной и с учётом квадратичного фазового множителя exp [ik (x2 + y2)/(4 f)] .

Если устремить в (16) z к нулю, то в пределе получим начальную амплитуду, совпадающую в безразмерных переменных с (14), где в2 = 2 f /zy = 4 f /(kw2).

3. Результаты моделирования

В табл. 1 показаны рассчитанные по формуле (16) распределения интенсивности и фазы для АЭГ-вихрей при разных топологических зарядах и на разных расстояниях z от начальной плоскости. Параметры расчёта: начальные радиусы перетяжки эллиптического Гауссова пучка w x = 123 мкм и w y =3 w x =369 мкм, длина волны – 532 нм. Из табл. 1 видно, что интенсивность АЭГ-вихрей (при n >0) представляет собой по внешнему виду два квазиэл-липтических Гауссовых пучка, большие оси которых лежат на одной прямой и которые разделены расстоянием L , зависящим как корень квадратный от величины топологического заряда n :

L = w y ( z ) V n ,                                 (22)

где радиус перетяжки Гауссова пучка по одной из координат при любом z имеет вид:

w y ( z ) = ( kfw y ) ^- 1 [ z ² ( z y + 2 f )² + z y ( z - 2 f )² ] 1 ^/2. (23)

Из (23) видно, что зависимость от расстояния z радиуса перетяжки у эллиптического Гауссова пучка отличается от такой зависимости для обычного Гауссова пучка.

При распространении в свободном пространстве АЭГ-вихри сохраняют свою структуру, меняются масштабно (расстояние между максимумами двух светлых пятен увеличивается) и вращаются вокруг оптической оси. При этом на самой оптической оси остаётся изолированный n -кратно вырожденный ноль интенсивности, фаза при обходе вокруг которого меняется на 2π n . Но и при n =0 АЭГ-вихрь, хо-

тя и не имеет вихревой составляющей (нуля интенсивности в центре), тем не менее, обладает ОУМ (остаётся астигматическая составляющая). Из (15) и соотношения начальных радиусов перетяжки w y = 3 w_x ( P 2 = 1/4, так как у ²- p ² = 2 и потому, согласно определению в и у , ( в w y / w_x )² - в ² = 8 в 2 = 2) следует, что ОУМ пучков в табл. 1 равен:

7 ^ = n + 4 i PL i ( 5/3 ) W 3 P „ ° ( 5/3 ) .

Из табл. 1 также видно, что АЭГ-вихри при любом n при распространении вращаются независимо от величины n против часовой стрелки. Можно показать, что угол поворота θ АЭГ-вихря как целого зависит от расстояния z следующим образом:

tg 9 =

1 2 f + 1 | z„

2 f

-

Из (25) видно, что при z =0 угол поворота равен θ =0 (пучок вытянут вдоль вертикальной оси, так как w y = 3 w x ), при z =2 f угол поворота равен θ = π /2 (пучок вытянут вдоль горизонтальной оси), а при z = f угол немного больше π /4 (так как z_y >>2 f при выбранных параметрах) и равен:

9 = arctg

f 2 f ,) — + 1

z„

Эти выводы подтверждаются углом поворота пучка в табл. 1.

4. Фокусировка эллиптических оптических вихрей с помощью цилиндрической линзы

Для подтверждения теории и расчётов было проведено экспериментальное наблюдение распространения АЭГ-вихрей. На рис. 1 показана оптическая схема установки, использованной в эксперименте. Эллиптический Гауссов лазерный пучок (λ =532 нм) с параметром эллиптичности 1:3 направлялся на дисплей пространственного модулятора света SLM (HOLOEYE, PLUTO-VIS). Модулятор света был использован для реализации фазовой маски в виде т ( r , ф) = ехр( i [ n ф + a x ]) (( r , ф) - полярные координаты, r ² = x ² + y ², a - пространственная частота несущей, n -топологический заряд), генерирующей внеосевой заданный вихревой пучок. Отражённый от модулятора и промодулированный по фазе эллиптический пучок с помощью комбинации линз L 1 , L 2 ( f 1 =350 мм, f 2 = 150 мм) и зеркал M 1 , M 2 направлялся на цилиндрическую линзу CL ₁ ( f ₃ = 100 мм), наклонённую под углом 45° градусов в плоскости, перпендикулярной оси распространения пучка. Система линз строила изображение плоскости, сопряжённой с плоскостью дисплея модулятора, в плоскости цилиндрической линзы z =0.

Табл. 1. Распределения интенсивности (строки 1, 3, 5, 7) и фазы (строки 2, 4, 6, 8), рассчитанные по формуле (16) для АЭГ-вихрей с параметром эллиптичности 1:3 и топологическими зарядами n = 0, 1, 3, 5, 7 на различных расстояниях от начальной плоскости: z = 0, z = f = 100 мм, z = 150 мм и z = 2f = 200 мм. Размер кадров 2300 × 2300 мкм

n = 0

n = 1

n = 3

n = 5

n = 7

SLM

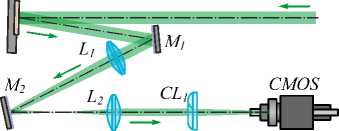
Рис. 1. Оптическая схема для исследования фокусировки эллиптических оптических вихрей с помощью цилиндрической линзы: SLM – пространственный модулятор света HOLOEYE PLUTO-VIS, M1 и M2 – зеркала, L1 и L2 – сферические линзы (f1 = 350 мм, f2 = 150 мм), CL1 – цилиндрическая линза (f3 = 100 мм), CMOS – видеокамера ToupCam U3CMOS08500KPA

CMOS-видеокамера, расположенная на оптическом рельсе, позволяла снимать формируемые распределения интенсивности пучка на различном расстоянии z от плоскости цилиндрической линзы. Изображения, полученные на расстояниях z =0, 100, 150 и 200 мм, представлены в табл. 2.

В табл. 2 видно, что при n =0 формируется одно эллиптическое световое пятно, а при n = 1, 3, 5, 7 формируется два пятна, причём при n = 1 эти пятна не успевают разойтись и между ними возникает интерференция.

Из сравнения табл. 1 и табл. 2 видно хорошее согласие теории и эксперимента.

Табл. 2. Распределения интенсивности, полученные для случая фокусировки эллиптических вихревых пучков с параметром эллиптичности 1:3 и топологическим зарядом n = 0, 1, 3, 5 и 7 на различных расстояниях от плоскости цилиндрической линзы: z = 0, 100 (фокусное расстояние), 150 и 200 мм (двойное фокусное расстояние). Размер кадров 2300 × 2300 мкм

n=0            n=1            n=3            n=5            n=7

ынкиш

На рис.2 показаны две интерферограммы, полученные для АЭГ-вихрей, показанных в табл. 2, при z =2 f и n = 1,3. Из рис. 2 видно, что действительно, в центре пучка сохраняется оптический вихрь с топологическим зарядом n = 1 (рис. 2 а ) и n =3 (рис. 2 б ). Интерферограммы для n =5,7 получились с низким контрастом полос, так как в промежутке между двумя локальными максимумами (табл.2) почти нулевая интенсивность света.

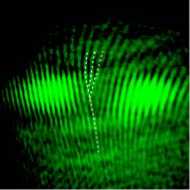
Рис. 2. Интерферограммы АЭГ-вихрей, полученных

на расстоянии z = 2f (табл. 2, строка 4) при n = 1 (а) и n = 3 (б)

Заключение

В работе получены следующие результаты. Найдено новое модовое решение параксиального уравнения Гельмгольца. Это решение описывает семейство неортогональных лазерных мод – астигматических эллиптических Гауссовых оптических вихрей. Такие пучки в начальной плоскости представляют собой изолированный n -кратно вырожденный ноль интенсивности, внедрённый в центр перетяжки эллиптического Гауссова пучка, главные оси эллипса которого расположены вдоль декартовых осей, прошедшего цилиндрическую линзу, ось которой повернута в начальной плоскости вокруг оптической оси на 45 градусов по отношению к декартовым осям. Радиусы перетяжки Гауссова пучка не произвольные, а связаны определённым соотношением. Найден нормированный на мощность пучка полный орбитальный угловой момент. Он равен сумме двух слагаемых, одно из которых равно топологическому заряду n оптического вихря, а второе слагаемое описывает вклад безвихревого астигматического эллиптического Гауссова пучка. Орбитальный момент таких пучков может быть дробным, целым или нулевым. Найденные модовые пучки при распространении сохраняют свою структуру, меняются только масштабно и вращаются вокруг оптической оси. На двойном фокусном расстоянии от цилиндрической линзы пучок поворачивается на 90 градусов. Распределение интенсивности таких пучков имеет характерный вид: два почти эллиптических световых пятна, большие оси которых лежат на одной прямой, и расстояние между максимумами этих световых пятен зависит как корень квадратный от величины топологического заряда и увеличивается при распространении пучка в свободном пространстве. Заметим, что в таких пучках из-за согласованности радиусов перетяжки эллиптического Гауссова пучка и угла наклона цилиндрической линзы, цилиндрическая линза не «снимает» вырождение центрального нуля интенсивности и не «разваливает» его на n разделённых в пространстве нулей интенсивности, как это принято считать [1].

Работа выполнена при поддержке Российского научного фонда (грант 17-19-01186) в частях «Амплитуда пучка на двойном фокусном расстоянии от цилиндрической линзы» и «Фокусировка эллиптических оптических вихрей с помощью цилиндрической линзы», Российского фонда фундаментальных исследований (грант 18-29-20003) в части «Семейство астигматических эллиптических Гауссовых вихрей» и Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части «Результаты моделирования».