Разработка активного RC-фильтра на операционных усилителях

Активные RC-фильтры на базе операционных усилителей нашли широкое применение в технике обработки аналоговых сигналов сравнительно низких частот. По сравнению с пассивными структурами (LC-фильтры и др.), активные фильтры обладают рядом преимуществ, а именно способностью усиливать сигнал, отсутствием необходимости использования индуктивностей, более простой настройкой. Наибольшее распространение получили частотно-избирательные фильтры Баттерворта, Чебышева, Бесселя, а также эллиптические. [1]

В данной статье рассматривается разработка фильтра нижних частот (Чебышева) с частотой среза 12000 Гц, коэффициентом передачи в полосе пропускания: 28, коэффициентом передачи в полосе задерживания: 4, максимальной неравномерностью амплитудно-частотной характеристики в полосе пропускания 3 Дб, с граничной частотой полосы задерживания 12500 Гц. Допуск на отклонение частоты среза 15%

Для расчета порядка фильтра нижних частот (ФНЧ) Чебышева воспользуемся формулой (1) и (2):

п =

J    а-2

(lOio—1)

(1010 - 1)

arch(—>)

—г

A a2 = 20/^— (2)

В соответствии с данными, описанными выше, подставим численные значения в формулу (1) для нахождения порядка фильтра. Порядок фильтра равен девяти (n=9). Теперь необходимо выяснить передаточную функцию проектируемого фильтра. ФНЧ Чебышева представляют собой каскадное соединение звеньев второго и первого порядков с передаточной функцией вида:

/ a       KC ® 2            a   kc®_c

K2(P) =         ——^, Ki(P) =     -.

p + Бюс p + C® c         p + Croc

Передаточная функция представляет собой произведение сомножителей, соответствующих звеньям первого и второго порядков. Коэффициенты, входящие в выражения для передаточной функции звеньев первого и второго порядка необходимо взять из таблиц для фильтра Чебышева, учитывая порядок фильтра. Суммарный порядок фильтра определяется, как сумма порядков составляющих его звеньев. ФНЧ состоят из нескольких звеньев второго порядка и одного звена первого порядка. Затем, по формулам (3) и (4) рассчитываем К1 и К2:

K 2 (p)

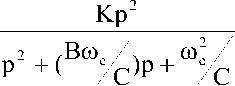
K 1 (P) =

Kp

p +

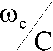
(4) Q =

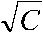
B

Подставим в формулы (3) и (4) численные значения, после расчетов которых получаем 4 звена второго порядка и 1 звено первого порядка. С целью проверки правильности расчета АЧХ фильтра и порядка фильтра построим график передаточной функции (Рисунок 1).

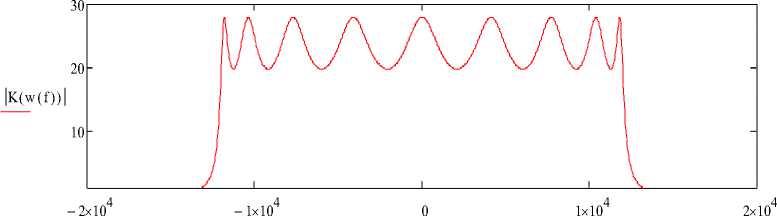
f

Рисунок 1. График передаточной функции.

На данном этапе все проводимые расчеты верны, а это значит что можно приступать к расчету принципиальной схемы фильтра. При выборе принципиальной схемы, прежде всего, нужно исходить из требуемой добротности звена, а также принять в расчет особенности настройки выбираемой схемы, величины номиналов резисторов и конденсаторов.[3] Добротность определим по формуле (5). Так как добротность равна 29, выбираем Биквадратную схему (рисунок 2), позволяющую получить как инвертирующее, так и не инвертирующее усиление (применяется при добротностях Q <  100 ). [2]

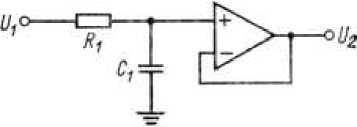
Рисунок 3. Схема ФНЧ первого порядка.

"Теория и практика современной науки"

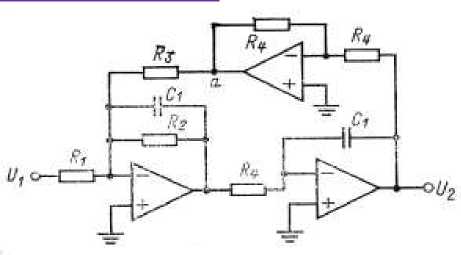
Рисунок 2. Схема биквадратного ФНЧ.

Расчет удобно вести в следующей последовательности:

• 1.    Выбираем С , =¹⁰ (6);

• 2.    Вычисляем R. =  ¹   , R = R -,

f C

• ⁴ ^ С    ¹ КС

R 2 = R ±, R 3 = R ^; (7) BC

Подставим и рассчитаем численные значения элементов четырёх фильтров второго порядка в соответствии с данными. ФНЧ первого порядка реализуется по схеме, представленной на рисунке 3. Расчет ФНЧ первого порядка, производится по формулам 8-11.

C 2 = ,  (8); ^R 1 = TTTF• (9) R 2 = ТЧ, (10) R 3 = KR ' (H)

f c             a c CC i           K - 1

Подставим и рассчитаем численные значения элементов одного фильтра первого порядка в соответствии с данными по формулам (8) и (9). ФНЧ второго порядка (или звено второго порядка в фильтре более высокого порядка) можно настраивать, ориентируясь на его АЧХ, представленную на рисунке 4.

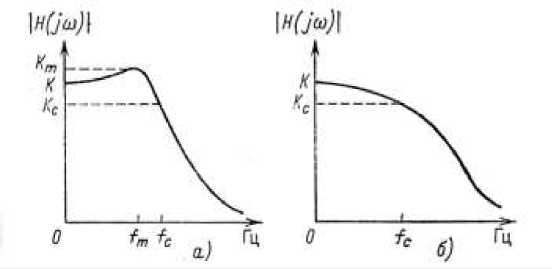
Рисунок 4. АЧХ ФНЧ второго порядка.

Для Q >  0.707 максимум АЧХ K_m имеет место на частоте f , где:

K

m

2 CK

B^ 1 4 С - B 2 ’

f = fc\C mC

^™

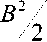
Частота среза ФНЧ настраивается с помощью R3, коэффициент передачи задается с помощью К = —, затем с помощью Rустанавливается fm. Вся R1               -           — процедура может быть повторена несколько раз. [3]

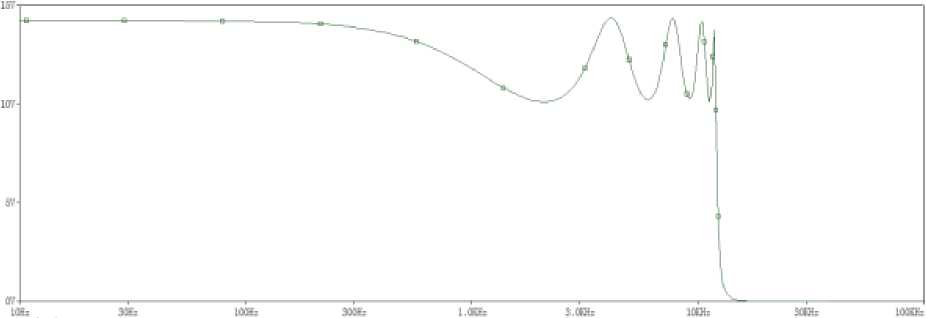
Рисунок 5. График АЧХ.

При выполнении данной работы, был разработан фильтр нижних частот c необходимыми параметрами, проанализированы его компоненты, рассчитан порядок, передаточная функция, а также была проведена его дальнейшая настройка. Весь математический расчет велся в программе MathCAD с последующим проектированием фильтра нижних частот и его компонентов в системе OrCAD. График АЧХ разработанного фильтра представлен на рисунке 5.