Разработка алгоритма компьютерного моделирования движения мобильного миниробота, перемещающегося с отрывом от опорной поверхности

Рис. 1. Схема движения прыгающего миниробота

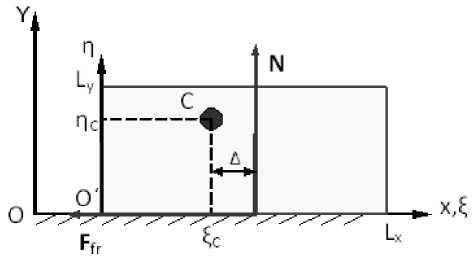
Рис. 2. Схема приложения сил и моментов

Плечо Δ нормальной реакции N должно находиться в интервале ( ^- ^ v , L a ^- ^ n ) , где L_x -длина корпуса. Уравнение моментов и в случае покоя, и в случае скольжения имеет вид:

N ⋅∆- F fr η С = 0

Принимая во внимание определение центра масс робота, для его координат имеем:

n

M ^ C = m ^ K + Е m^i , i = 1

n мПс = тПк +E тП ■ i =1

Здесь M = m + ^ m, - общая масса корпуса и i = 1

масс; ^ к , П К — координаты центра тяжести корпуса. Тогда, учитывая ограничения для плеча, придем к неравенству

0 <  F fr ^ c + N ^ c <  NL x

которое служит условием неопрокидывания. Выполнение (1) зависит как от коэффициента трения, так и от геометрических параметров робота, поэтому в общем случае принимать корпус даже в предположении безотрывного движения по поверхности за материальную точку нельзя. Однако зная интервал значений силы трения, можно убедиться, что для выполнения неравенства (3) достаточно, чтобы координаты центра масс и коэффициент трения находились в соотношении fоПс < min{^c, Lx - ^с }

При достаточно симметричном расположении внутренних масс последнее неравенство, как правило, выполняется, поэтому большой класс задач динамики роботов, скользящих на плоской поверхности, можно изначально упростить сведением к задаче движения материальной точки.

Очевидно, что в зависимости от суммарных проекций сил инерции корпус робота может оставаться неподвижным, может перемещаться по предоставленной поверхности без отрыва или двигаться с отрывом от нее. При этом в общем случае движение робота в пространстве является свободным. Физические условия контакта корпуса робота с поверхностью, по которой он перемещается, таковы, что поверхность сопротивляется проникновению корпуса внутрь, но не сопротивляется отрыву. Поэтому сила нормального давления N, вызванная контактом корпуса робота с плоскостью опоры, может быть направлена вертикально вверх или равняться нулю, т.е., удовлетворять условию N<0. Если в дальнейшем движение корпуса происходит без отрыва от плоскости опоры, то, в соответствии с (2), получим ограничение на относительное ускорение внутреннего тела, колеблющегося вдоль вертикали nn m + ^mi Ig + ^mini ^ 0

i = 1      J        i = 1

Если внутренние массы движутся таким образом, что в некоторые промежутки времени неравенство (6) нарушается, то корпус миниробота будет отрываться от поверхности, а движение робота приобретет прыжкообразный характер [6]. Тем не менее, выполнение неравенства (6) не гарантирует прижатия всей грани корпуса, так как нормальная реакция поверхности является силой, распределенной по площади соприкосновения. Ее интенсивность n ( х ) может принимать только неотрицательные значения, поскольку отсутствует прилипание, и условно картина распределения имеет вид, аналогичный показанному на рис. 3.

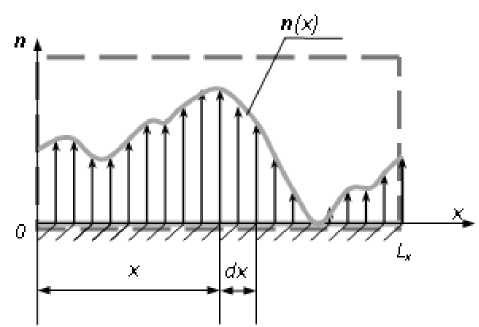
Рис. 3. Схема распределения нормальной реакции поверхности

Данная система нагрузки имеет равнодействующую в крайней точке тогда и только тогда, когда интенсивность во всех прочих точках контакта равна нулю. Действительно, если равнодействующая приложена в крайней левой точке, то алгебраический момент нагрузки относительно точки О, определяемый Lх как интеграл MO (N) = J n(х)xdx, равен нулю, что 0

при x >0 выполнится лишь при n ( 5 )=0 во всех точках касания, кроме нулевой. Если точка приложения является крайней правой точкой нагрузки, то разность между моментами равнодействующей и нагрузки равна:

L х                 L х

N • L + J n ( х ) xdx = J n ( х )( L_x - х ) dx ⁰⁰      .   (6)

Очевидно, что эта разность обращается в ноль только при нулевой интенсивности во всех точках, кроме правой.

Для составления алгоритма численного расчета параметров движения робота обратимся к примеру движения материальной точки под действием периодической вынуждающей силы (рис. 4) [7]. Точка может служить идеальной моделью рассматриваемого мобильного миниустройства, если пренебречь его размерами.

значение силы трения покоя, т.е., перестанет выполняться неравенство

I O x ( t )| < fN

В этом случае тело приобретает ускорение, определяемое разностью проекций вынуждающей силы и силы трения

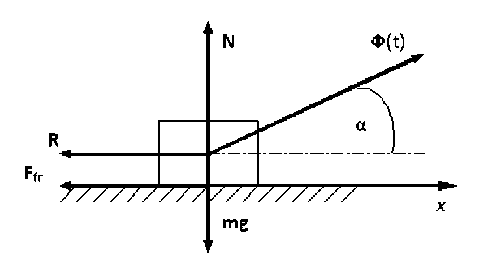
Рис. 4. Схема сил, приложенных к роботу

^mx = ^O x ^{( t} ) — f sgn ^O x ^{( t} ) • ^N

Это ускорение приводит к появлению скорости, и последующее направление трения будет противоположно не проекции силы (которая меняет знак в общем случае не одновременно с изменением направления движения), а противоположно скорости. Таким образом, ускорению уже начавшегося движения соответствует выражение mx = Ox (t) — f sgn о • N

Пусть модель перемещается по горизонтальной шероховатой плоскости. Будем рассматривать движение под действием силы тяжести mg , нормальной реакции N , силы сухого трения F fr , вязкого сопротивления R и периодической силы Ф(t) , направленной к поверхности под углом α (рис.2). Модуль вынуждающей силы изменяется по закону:

О ( t ) = О ₀ sin( tot + ф₀ )

где ω – частота, φ 0 – начальная фаза.

В состоянии покоя тела сила трения, как составляющая полной реакции плоскости, уравновешивает проекцию гармонической силы на ось х , т.е., ее горизонтальная проекция определяется равенством:

F_f = — O ₅ ( t ) = — O _o sin( to t + ф₀ ) cos a x

Направление силы трения в покое противоположно проекции силы Ф(t) . Пока тело остается неподвижным значение силы трения не превышает максимального, определяемого равенством

F fr™ = fN max

,

где     f    –    коэффициент    трения,

N = mg — О (t) sin a - значение нормальной реакции, которое предполагаем всегда положительным.

Тело начнет двигаться, когда проекция вынуждающей силы превысит максимальное

Здесь и в дальнейшем будем рассматривать кусочно-непрерывную функцию проекций Х скоростей или внешних сил (кроме трения) на ось х : f(X) = –f sgn X , которая позволяет определить коэффициент и направление трения одновременно. Скорость и координату, как в момент начала скольжения, так и в процессе движения будем определять численно при помощи разложения в степенной ряд.

Остановке тела соответствует значение скорости, равное нулю. Уменьшение скорости происходит за счет проекции равнодействующей всех действующих сил, в том числе и силы трения, которая направлена так же, как и трение – противоположно движению. Таким образом, если тело после остановки сразу же возобновит движение, то в направлении, обратном предшествующему. Опишем последовательность действий алгоритма компьютерного моделирования движения мобильного миниробота, перемещающегося с отрывом от опорной поверхности. Обобщенная блок-схема алгоритма представлена на рис. 5.

Алгоритм вычисления основывается на следующих допущениях. Прежде всего, в движении выделяем две фазы: I – полет, II – движение по поверхности. Переход из одной фазы в другую происходит или при выполнении условий отрыва (II→I), или при выполнении условий приземления (I→II). Условием отрыва является равенство нулю нормальной реакции поверхности, условие приземления – невыполнение неравенства y1>y1min для значений вертикальной координаты центра проекции корпуса. Величина минимального допускаемого значения координаты центра проекции y1min зависит от выбора начала отсчета. Например, если горизонтальная координатная плоскость проходит через центр, то y1min=0. Программа организована в виде цикла, выход из которого осуществляется, как только расчетное значение времени превысит заданную величину. Для численного расчета параметров движения использовался метод Эйлера II порядка.

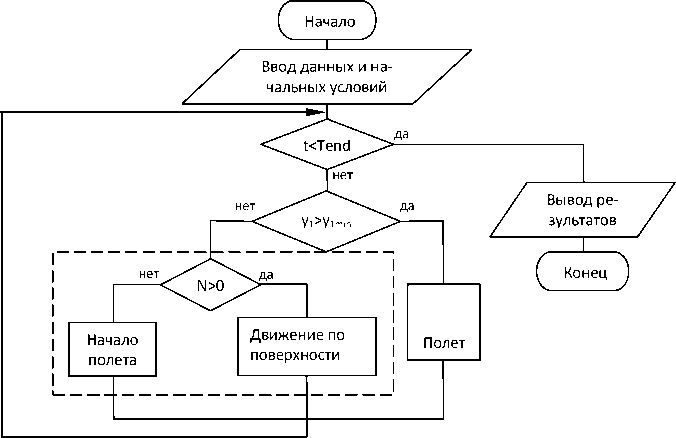
Рис. 5. Блок-схема алгоритма

Скорость и координату, приобретенные точкой на шаге, будем искать, разложив решение в степенной ряд Тейлора, который для произвольной функции имеет вид:

У ⁽ x ) = У 0 + У '( x o ⁾⁽ x

—

x o ) + ¹ У 4 x o ⁾⁽ x ^— x o⁾² + •••

Таким образом, ускорение каждой из обобщенных координат q j , j=1,2,3 , будем находить из правой части уравнений системы (2) в случае полета, или из уравнений (1) в случае движения по поверхности. Тогда, если ⁽ q j ) i — 1 – ускорение обобщенной координаты в начале i- го шага, т.е., определенное для предшествующего шагу момента времени t i-1 = Δ ( i – 1), то скорость и координата, согласно разложению, определятся выражениями:

⁽ q j ) i = ⁽ <7 j ) i — i + ⁽ q j ) i — i "A

1,

⁽ < j ) i = ⁽ < j ) i — i + ⁽ < j L i " ^A + -⁽ < j L i ■ ^{A 2}              .  (15)

Здесь Δ – выбранный шаг по времени.

Особенностью расчета, проводимого в блоке, выделенном пунктиром, является то, что начальные значения вертикальной скорости и координаты равны нулю. Так как в момент приземления робот испытывает удар с потерей кинетической энергии, то на первом шаге в блоке все начальные кинематические величины, кроме угла поворота и горизонтальной координаты, принимаем равными нулю, а угол поворота и горизонтальную координату оставляем неизменной с предыдущего шага. В общем случае блок «Движение по поверхности» должен использовать алгоритм, предусматривающий как возможность перемещения системы, так и возможность продолжительной остановки корпуса под действием сил трения. Результаты проведенного компьютерного моделирования движения мобильного миниробота, перемещающегося с отрывом от опорной поверхности представлены на рис. 6.

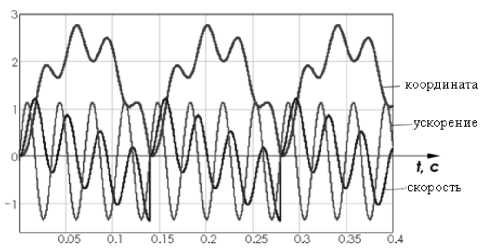
Рис. 6. Результаты компьютерного моделирования движения мобильного миниробота

Анализ полученной зависимости высоты прыжка от частоты вращения внутренней массы создает возможности управления движением миниробота, позволяющие задавать направление движения всего устройства и регулировать его скорость.

Работа выполнена в рамках реализации Федеральной целевой программы «Научные и научнопедагогические кадры инновационной России» на 2009-2013 годы (гос. регистр. № П699, шифр НК-617П-4).