Разработка алгоритма нахождения оптимального пути для нефтеперевозок с учетом расположения общественных мест

Транспортировка нефтесырья между точками добычи, переработки, хранения сбыта или потребления является одним из ключевых процессов в нефтяной промышленности. Когда дело касается нефтепродуктов, необходимо соблюдать меры безопасности, так как большинство их видов опасны для окружающей среды и здоровья живых организмов. Транспортировка опасных грузов, включая нефтепродукты, регламентированы многими правилами, которые описывают требования состояния машины для перевозок, характеристики цистерны или тары для хранения груза, поведение водителя и т.д. Приказ №234 от 24. 08. 94 г. «Об утверждении Инструкции по обеспечению безопасной перевозки опасных грузов авто-мобильным транспортом.» выдвигает требования: при перевозке опасных грузов (ОГ) автомобильным транспортом на пути не должны находиться:

• •    крупные промышленные объекты;

• •    крупные населённые пункты и зоны отдыха;

• •    архитектурные сооружения, природные заповедники;

• •    охраняемые природные территории.

Представим дорожную сеть в виде графа G=(V,E) , а расположение общественных, промышленных и охраняемых мест в виде множества точек P . Поставлена задача нахождения кратчайшего пути между точками A и B для перевозки ОГ. Перед нахождением кратчайшего пути необходимо исключить из графа дорожной сети G ребра, расположенные на расстоянии 100 м от каждой точки множества P . Расстояние от точки до прямой можно вычесть через формулу аналитической геометрии:

d = |(У1 - У2) • Px + (^2 - *1) • Ру + (*1У2 - ^У1)| 7(У1 -У2)2 + (^2 -^1)2

, где Х 1 ,у 1 — координаты первой вершины ребра, х₂,у₂ — координаты второй вершины ребра, р _х , Р у — координаты точки p из множества P .

Таким образом, для каждой точки p из множества P найдем те ребра из множества E, у которых расстояние d <  R_B3, где R_B3 - радиус поражения в случае взрыва нефтепродукта, и исключим их графа G (так же исключим изолированные вершины графа, которые могли потерять связь с остальными вершинами из-за исчезновения ребер).

Один из самых распространённых алгоритмов в теории графов для нахождения кратчайшего пути между двумя вершинами — алгоритм Дейкстры.

Суть алгоритма заключается в том, что для каждой вершины рассчитывается параметр – минимальное известное расстояние от начальной точки А . Работа алгоритма Дейкстры представляет собой цикл, на каждом шаге которого посещается ближайшая вершина графа, рассчитывается у нее расстояние и, если это расстояние оказывается минимальным, то оно записывается для этой вершины.

В начале работы алгоритма у всех вершин число a , которое обозначает короткий путь из начальной точки до этой вершины, равно бесконечности. У самой начальной точки A число a равно 0.

Если на графе существуют не посещенные вершины, то выбираем не посещённую вершину u , имеющая минимальное число a . Из выбранной точки u рассматриваем все пути, идущие от нее до соседних точек. Для каждой соседней вершины v рассчитываем минимальный путь, который равен сумме a( u ) и веса ребра. Если соседняя вершина v уже имеет a отличное от бесконечности, то проверяем, если рассчитанное на этом шагу число меньше числа a( v ) , то

a( v ) = a( u ) + l

, где l – вес ребра. После рассмотрения всех соседей вершина u помечается как просмотренная и шаг цикла заканчивается. Если на графе не осталось не посещенных точек, то цикл завершается. После работы алгоритма конечная точка будет иметь число a, которая обозначает минимальный возможный путь из начала вершины.

Алгоритм Дейкстры часто используется в математических абстрактных графах, однако, на геометрических графах, которыми являются дорожные сети и другие линейные объекты, он не учитывает параметры искомого маршрута. Поэтому алгоритм, вместо того чтобы идти из начальной вершины по направлению к конечной точке, расширяется в виде «круга» от исходной точки, рассматривая таким образом и те точки, которые находятся в противоположной стороне от искомой. Алгоритм А* является доработанной версией алгоритма Дейкстры. Добавляя эвристическую оценку, которое представляет собой физическое расстояние от рассматриваемой точки до конечной точки, алгоритм дает приоритет тем точкам, которые географически ближе к искомой вершине. Таким образом, не теряется время и производительность на расчет вершин, которые отдаляются от конечной.

Принцип алгоритма А* схож с алгоритмом Дейкстры, за тем исключением, что помимо числа a — длина пройденного пути, находится число b – физическая длина до конечной точки, а приоритет будет отдаваться той не пройдённой вершине, у которой a+b наименьший.

Построить маршрут по результатам работы алгоритма

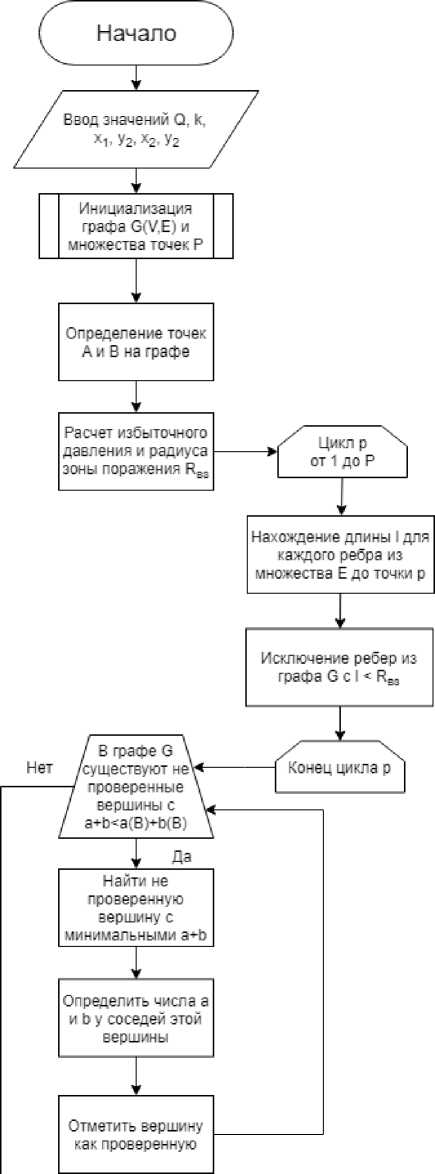
Рисунок 1 — Алгоритм нахождения оптимального пути для нефтеперевозок с учетом расположения общественных мест

Таким образом, проанализировав алгоритм исключения ребер из графа по положению общественных, природных и промышленных зон и алгоритм A* можно составить разработать порядок действий, который будет осуществлен для нахождения оптимальных маршрутов для перевозки опасных нефтегрузов. Алгоритм определения оптимального пути показан на рисунке 1.

Вначале определяем переменные Q, к, х₁,у₁,х₂/у₂, где Q — масса нефтепродукта, который будет перевезен, k — коэффициент взрывчатой силы нефтепродукта к взрывчатой силе тротила, х₁,у₁ — координаты начальной точки А , х₂,у₂ — координаты конечной точки B . По переменным Q, к рассчитывается радиус поражения /?_вз , по которому будут выбираться опасные для перевозки пути. После определения графа дорожных путей G(V,E) и множества точек P — положение общественных, природных, производственных зон, по географическим координатам х ₁ ,у ₁ ,х ₂ ,у ₂ определяются начальные и конечные вершины A и B на графе.

После работы алгоритма исключения ребер и алгоритма A* строится короткий путь по вершинам графа и геовизуализируется маршрут на карте.

Заключение

В данной статье были разработан алгоритм определения оптимального пути для перевозки опасных нефтегрузов. Алгоритм включает в себя поиск A*, который является доработанной версией алгоритма Дейкстры.

Проанализировав требования к перевозкам опасных грузов было выявлено, что не все дорожные пути подходят к транспортировкам взрыво-, огнеопасных веществ. Поэтому был разработан алгоритм, исключающий эти пути в зависимости от расположения дороги к больницам, зонам отдыха и другим общественным зонам.

Результат алгоритма будет показан на карте для принятия решения выбора маршрута.